开孔倾斜平板消波效果试验研究

王国玉,赵唯佼,项竹青,朱干城

(大连理工大学海岸和近海工程国家重点实验室,辽宁 大连 116024)



开孔倾斜平板消波效果试验研究

王国玉,赵唯佼,项竹青,朱干城

(大连理工大学海岸和近海工程国家重点实验室,辽宁 大连 116024)

对开孔倾斜平板在二维规则波作用下的消波效果进行了物理模型试验研究,在平板与静水面夹角为±15°的情形下,比较分析了平板开孔率为0%、10%、20%和30%时,其对波浪反射系数、透射系数的影响以及能量衰减系数随着相对宽度(平板宽度与波长之比)的变化关系。研究结果表明,两种不同夹角情形下,倾斜平板在与静水面成15°时的消波效果要优于-15°,相对宽度和开孔率均影响平板的消波效果。

平板;开孔率;波浪;消波;试验研究

透空式防波堤是一类下部透空、上部连续的挡浪结构,可以使堤前波浪的能量大部分不能向堤后传播。透空式防波堤结构由Weigel[1]于1961年提出,近年来逐渐被重视,国内外许多学者对其进行了研究。Yip等[2]基于线性波浪理论,在运用达西基本定理的基础上对小角度倾斜淹没带孔薄板进行了研究。Liu等[3]对短波与淹没水平板(有限厚度)的相互作用机制进行了理论分析,并求解得到了相应的解析解。Williams等[4]基于Wiener-Hopf和残数积分方程的一种新的联合求解方式从理论上分析了淹没半无限长弹性板与线性波的作用机制。张志强[5]基于线性波浪理论,运用边界单元方法,研究了不同组合形式的水平板式防波堤在深水情况下的水动力特性,给出了波浪反射系数、透射系数和板宽与波长之比以及相对板间距之间的关系。Stoker[6]对一块水平板始终固定在自由水面时的波浪入射进行了研究,得到了长波入射条件下的反射系数和透射系数公式。Ijima等[7]运用波浪色散方程将特征值展开,研究了有限水深情况下浮于自由水面的水平板绕射问题,通过理论分析和物理模型试验探究了水平板防波堤的消浪效果。Hattori[8]进行了淹没水平板的试验研究,在将水平板分别处于水面、水面下1/4水深、水面下1/2水深等3种不同情形下研究其消浪性能。Siew等[9]研究了淹没水平板附近长波的反射和透射特性,将水平板所在空间划分为上、下、前、后4个单一区域,得到了反射和透射所满足的控制方程组。Brossard等[10]通过试验论证了水平板淹没深度与试验水深比以及波数对反射系数和透射系数的影响,试验中采用移动式波高仪观测并研究了试验过程中的能量转换机制。Rao等[11]对淹没水平板进行了全面的物理模型试验研究。刘丹[12]借鉴前人的研究成果,对由2种不同宽度组成的水平板防波堤消浪结构进行了物理模型试验,研究了板宽与波长之比以及波高与波长之比对该类结构消浪效果的影响,对反射系数和透射系数进行了分析。Burke[13]基于Wiener-Hopf的傅里叶变换方法对微幅波与淹没水平板作用下的散射现象进行了理论分析,运用数学公式对反射系数和透射系数进行了描述。Patarapanich[14]运用数值计算方法对淹没水平板的消波性能进行了计算,得到了零反射以及最大反射系数与水平板宽与波长之比、水平板淹没深度与试验水深之比、试验水深与波长之比的关系。Nallayarasu等[15]在淹没水平板的研究基础上,运用有限元数值计算方法研究了有限深度情况下的淹没倾斜水平板的波浪力问题。王科[16]运用数值方法模拟了波浪与淹没水平板的相互作用,发现板宽与波长之比以及水平板淹没深度与水深之比是影响该类结构消波效果最重要的两个因素。同时还进行了相应的物理模型试验来研究此类结构的特性,得到了波浪经过水平板的透射曲线,以及最佳消浪效果的试验条件。

上述研究工作大多是针对波浪与实体平板结构的相互作用而开展的。另外,有研究[17-18]表明,实体结构开孔对于改善其水动力学性能有很大的贡献。为此,本文对不同倾斜角度的平板结构在不同开孔率条件下的消浪效果进行试验研究。

1 物理模型试验

物理模型试验在大连理工大学海岸和近海工程国家重点实验室的波流水槽中进行,水槽尺寸为22 m×0.45 m×0.6 m (长×宽×高)。水槽前端装有电机式造波机,可产生平稳、重复性好的规则波,水槽末端安装有消能网,用于吸收波浪能量,减少波浪反射。

试验过程中的波面历时数据由大连理工大学海岸及近海工程国家重点实验室自主研制生产的LG-30型浪高仪进行采集。LG-30型浪高仪的测量量程为0.30 m,绝对误差小于0.001 m,试验前对所有参与测定波面的浪高仪进行标定,其线性度大于0.999,满足试验精度要求。

试验水槽中模型及仪器的布置如图1所示。平板透空式防波堤模型放置于水槽中间偏后的位置,模型前布置1号和2号两个浪高仪,间距Δl1=0.210 m,模型后布置3号和4号两个浪高仪,间距Δl2=1.470 m,分别同时记录这4点的波面数据。对1号和2号浪高仪测得的数据通过Goda两点法[19],分离入射波高和反射波高,可得出模型对波浪的反射系数。对于3号和4号浪高仪测得的波面数据,通过上跨零点法统计波高并取平均值作为透射波高,从而确定透射系数。

图1 试验水槽示意图

实体平板透空式防波堤模型平面图如图 2(a)所示,其对应开孔率为零，图2(b)(c)(d)分别是开孔率为10%、20%和30%的开孔平板模型平面图。平板材料均采用宽度为450 mm、厚度为10 mm的有机玻璃制作。在板材的四角开孔,4根螺纹杆分别由四角的空洞穿过,上下由螺母固定,螺纹杆焊接在底部铁板上,这样就构成了平板透空式防波堤(图3)。试验中,将模型放置在水槽底部,同时通过上方的支架将模型紧固,保证模型在波浪作用下不发生变形和位移。

图2 平板透空式防波堤模型平面图(单位：mm)

图3 制作好的试验模型照片

物理模型试验采用规则波浪,波要素如下:试验水深为0.4 m,波浪高度分别为0.04 m、0.08 m;波浪周期分别为0.73 s、0.91 s、1.10 s、1.28 s和1.46 s,对应的波长分别为0.83 m、1.25 m、1.70 m、2.12 m和2.53 m。

试验中的主要物理参数包括:水深h,波高H，周期T，波长L,平板与静水面的夹角θ,开孔率e,平板宽度W,反射系数Kr,透射系数Kt,波能衰减系数Kd。

模型试验分别对θ为15°和-15°的平板透空式防波堤模型进行了观测,开孔率分别为0%、10%、20%、30%。每组试验重复3次,取其平均值作为最后试验结果。试验中采用的采样间隔为0.02 s,采样数为1 024个。

图4(a)和图4(b)分别给出了15°和-15°布置时平板透空式防波堤的试验照片。试验可以观察到由于结构与波浪的相互作用,波浪形态发生改变甚至破碎,波能衰减,从而起到消波的作用。在不同周期的入射波作用下,能量衰减的程度不同,消波效果有明显差异,波浪周期较短时,波浪破碎现象明显,消波效果显著。与15°布置时不同,当平板布置成-15°时,其对波浪的反射作用明显增强,模型前波面起伏变化较大,透过模型后的波浪幅值降低,但经过平板结构时,波浪破碎的现象并不明显。

图4 平板透空式防波堤试验照片

2 试验数据分析

对于采集到的模型前面的波面历时数据,由Goda两点法,可将模型前面的入射波高Hi和反射波高Hr分离,从而得到平板对波浪的反射系数为

(1)

对于采集到的模型后面的波面历时数据通过上跨零点法,可统计得到模型后面的透射波高Ht,进而得到平板对波浪的透射系数为

(2)

另外,在考虑波浪总能量时,可以定义波能衰减系数为

(3)

波能衰减系数反映了结构物对波浪能量的耗散和损失能力,Kd值越大,表明波浪经过结构物时,由于波浪破碎等原因引起的波浪能量损失越大。

物理模型试验主要对比分析了15°平板透空式防波堤与-15°平板式透空式防波堤的消波性能,并探讨了开孔率等因素对消波效果的影响。

2.1 15°和-15°平板结构消波性能对比

进行了0.04 m波高时,15°平板透空式防波堤和-15°平板透空式防波堤的消波性能观测。图5给出了不同开孔率的平板结构在不同波浪周期条件下对波浪的反射系数随着相对宽度W/L变化的试验结果。结果表明：15°平板透空式结构的反射系数Kr随着相对宽度的增大逐渐变小，当开孔率为20%和30%时,其对波浪的反射系数较小,约为0.1；-15°平板透空式结构的反射系数Kr随着相对宽度的增大先增大后逐渐变小,且在相对宽度约为0.25时,即平板的水平宽度约为1/4波长时出现峰值；在开孔率一致的条件下,与15°平板透空式结构相比,-15°平板结构对波浪的反射系数较大,这与试验中观察到的现象是一致的；随着开孔率的增加,由于结构的透水性增强，15°和-15°平板结构对波浪的反射作用均减弱,反射系数降低。

图5 平板对波浪的反射系数随相对 宽度的变化(H=0.04 m)

图6给出了15°和-15°时不同开孔率的平板结构在不同周期波浪作用下对波浪的透射系数随着相对宽度的变化。15°和-15°两种情形下,平板结构对波浪的透射系数的变化规律较为一致,均随着相对宽度的增大而减小,表明结构在短周期波浪作用下掩护效果较佳。对于开孔率为0%的实体平板结构,在相对宽度大于0.25时,可以使透射系数降低至0.5以下。比较而言,15°平板结构的消波效果优于-15°平板结构。随着平板开孔率的增加,波浪的透射作用逐步增强。当开孔率达到30%时,对于-15°的平板结构,在试验范围内,其对波浪的透射系数均大于0.5。

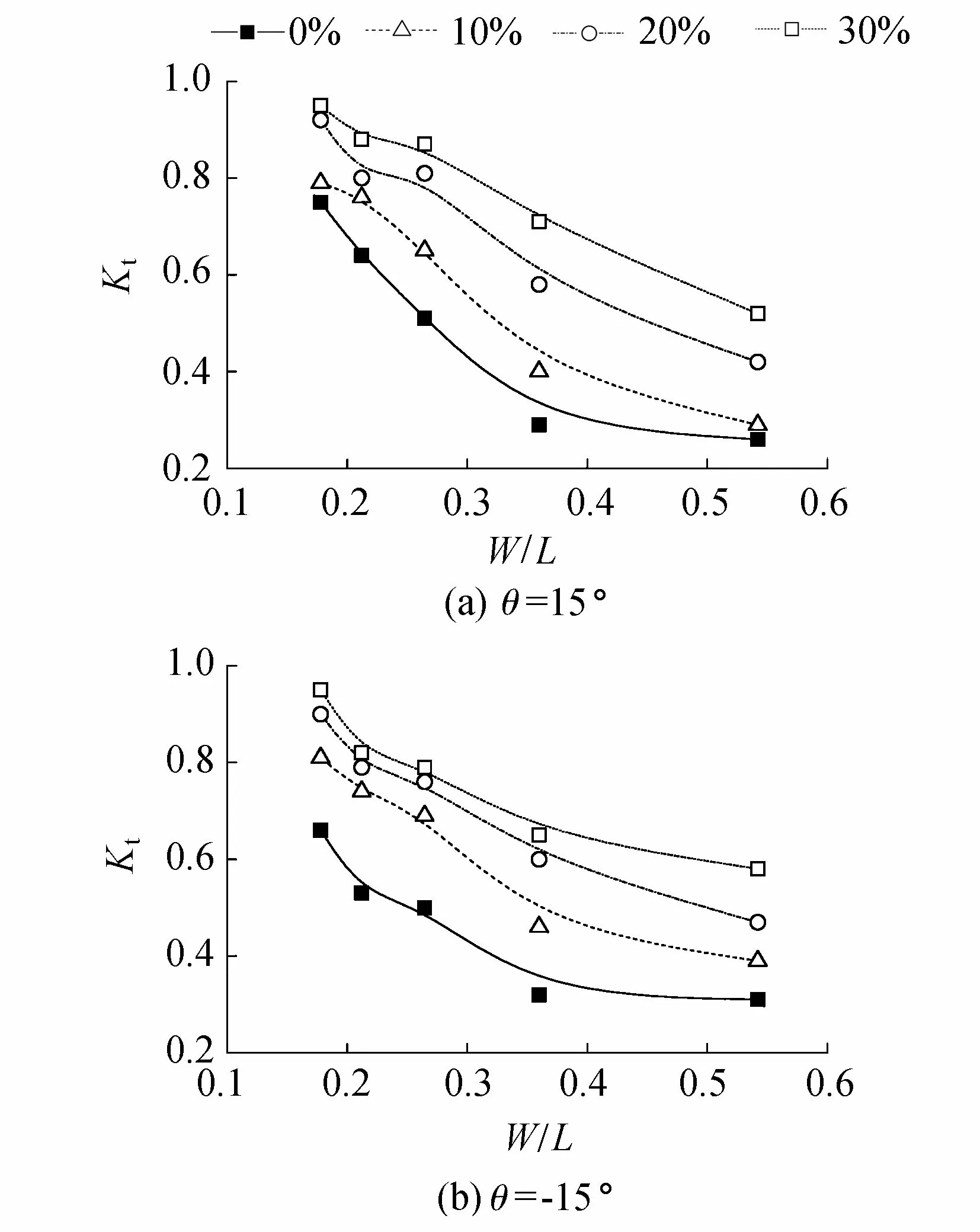
图6 平板对波浪的透射系数随相对 宽度的变化(H=0.04 m)

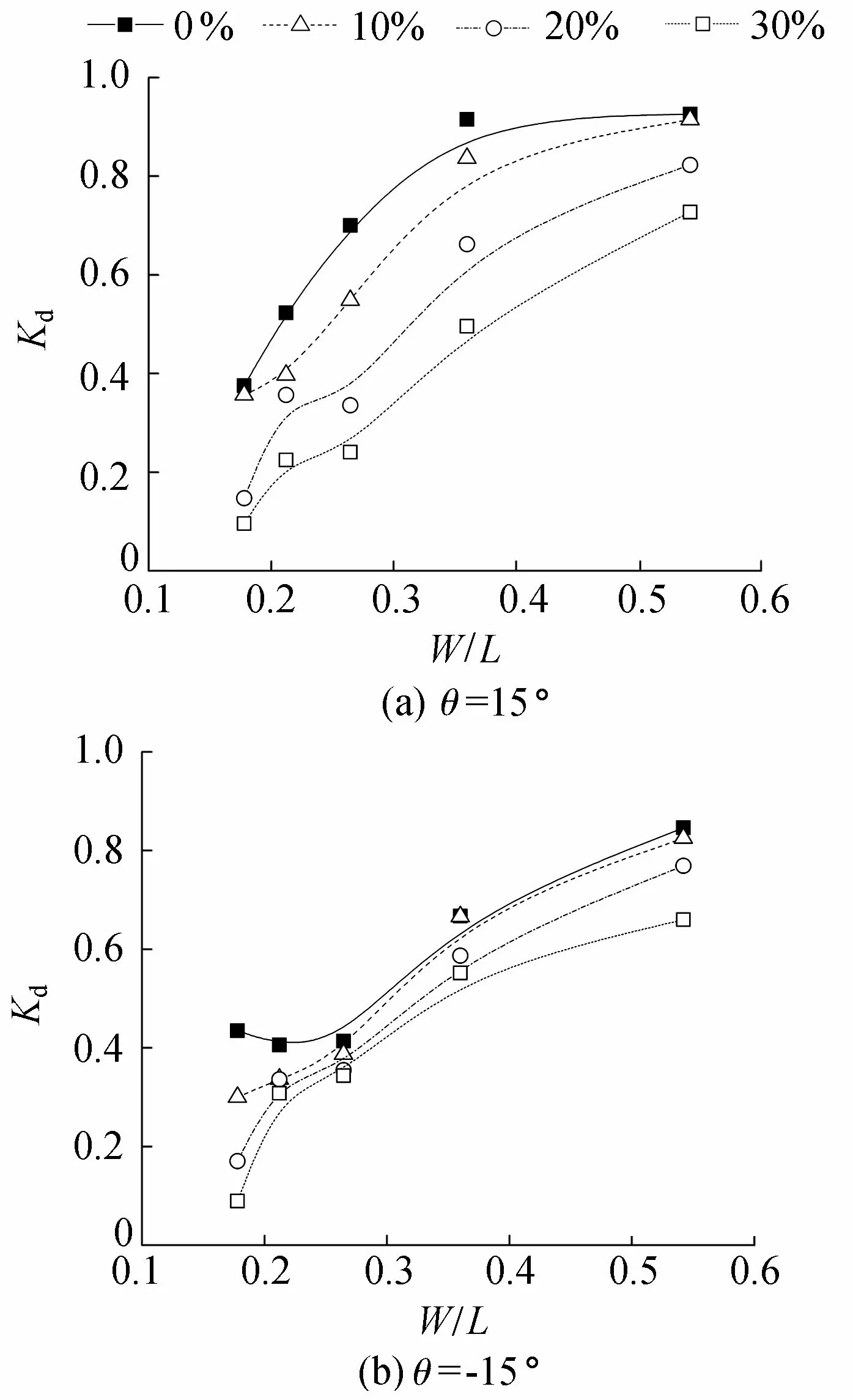
图7 平板对波浪的能量衰减系数随相对 宽度的变化(H=0.04 m)

图7给出了15°和-15°时不同开孔率的平板结构在不同周期波浪作用下对波浪的能量衰减系数随着相对宽度的变化。总体上看,能量衰减系数随着相对宽度的增加而变大,表明这种倾斜的平板结构对于短周期波浪的能量耗散作用更强。并且,随着开孔率的增加,两种情形下单层平板对波浪能量的耗散作用减弱。比较而言,15°平板结构对波浪能量的衰减作用要强于-15°平板结构。

同时进行了0.08 m波高时,15°平板透空式防波堤和-15°平板透空式防波堤的消波性能观测,其规律性与入射波高为0.04 m时较为类似。

2.2 开孔率对平板结构消波性能的影响

为了进一步探讨平板结构的开孔率对其消波性能的影响规律,对不同开孔率的平板对波浪的反射系数、透射系数以及能量衰减系数进行了比较分析。

以入射波高H=0.04 m为例,图8给出了不同周期入射波浪作用下15°和-15°平板对波浪的反射系数随着开孔率e的变化。在平板与静水面夹角为15°时,平板在静水面附近形成一个15°的缓坡,波浪传播至平板位置时,部分波浪被反射回去,在平板上方,波浪由于发生浅水变形而产生破碎等现象,波浪能量因而衰减,透射波高降低。在平板与静水面夹角为-15°时,平板在静水面附近形成一个“楔形”的结构,波浪传播到该位置时,由于“楔形”平板的阻挡作用,结构对波浪的反射作用较强,表现出反射系数较15°时有所增大,最大反射系数在平板不开孔时可达0.6。两种布置方式下,随着开孔率的增加,平板对波浪的反射作用均减弱,反射系数亦随之降低。比较而言,θ=-15°时,随着开孔率的增加,平板对波浪的反射系数降低较快。

图8 平板对波浪的反射系数随开孔率的 变化(H=0.04 m)

图9给出了入射波高为0.04 m时,不同周期入射波浪作用下15°和-15°平板对波浪的透射系数随着开孔率的变化。比较明显的是,随着开孔率的增加,波浪的透射作用增强,两种布置方式下,平板的透射系数均有所增大。对于周期较短的波浪,如T=0.73 s情形,在试验选取的开孔率范围内(0%～30%),透射系数大多可降低至0.5以下。

图9 平板对波浪的透射系数随开孔率的 变化(H=0.04 m)

图10 平板对波浪的能量衰减系数随开孔率的 变化(H=0.04 m)

图10给出了入射波高为0.04 m时,不同周期入射波浪作用下15°和-15°平板对波浪的能量衰减系数随着开孔率的变化。很明显,随着开孔率的增加,单层平板的透水性增强,两种布置方式下平板对波浪能量的耗散作用均减弱。并且,对于不同周期的入射波浪,平板对波浪的能量衰减作用明显不同。当入射波浪周期比较小时,如T=0.73 s时,Kd大于0.7。这表明,对于T=0.73 s的短周期波浪,倾斜的单层平板在开孔率0%～30%的范围内,均可以衰减掉70%以上的波浪能量,对于T=0.91 s的入射波浪,也可以衰减掉50%以上的波浪能量。

3 结 语

通过物理水槽中的规则波试验,对开孔倾斜平板的消波效果进行了初步研究。在平板与静水面成15°和-15°两种情形下,得到了不同开孔率时平板对波浪的反射系数、透射系数以及能量衰减系数随着相对宽度的变化关系。试验现象和数据表明,-15°平板对波浪的反射作用较强,15°平板对波浪能量的耗散作用更强,消波效果更优。开孔率对平板的消波效果有较大影响。对于短周期的入射波浪,在本试验的开孔率范围内,可衰减50%以上的波浪能量。

平板开孔后,尽管波浪的透射作用增强,但作用在平板上的波浪力有所降低。作为后续研究工作,开孔平板上的波浪力将是主要内容,在消波效果和结构受力之间的平衡将成为工程人员关注的焦点。

[1] WEIGEL R L. Closely spaced piles as a breakwater[J].The Dock and Harbour Authority,1961,42:150.

[2] YIP T L,CHWANG A T. Water wave control by submerged pitching porous plate[J].Journal of Engineering Mechanics,1998,124(4): 428-434.

[3] LIU P L F,ISKANDARANI M. Hydrodynamic wave forces on submerged horizontal Plate[C]//Proceeding of the Congress.Ottawa: IAHR,1989: 51-64.

[4] WILLIAMS T D,MEYLAN M H. The Wiener-Hopf and residue calculus solutions for a submerged semi-infinite elastic plate[J]. Journal of Engineering Mathematics,2012,75(1): 81-106.

[5] 张志强.组合板式防波堤水动力特性研究[D].大连: 大连理工大学,2010.

[6] STOKER J J. Water waves[M]. New York: Interscience,1957.

[7] IJIMA T,OZAKI S,EGUCHI Y,et al. Breakwater and quay wall by horizontal plates[J].Proceedings of Coastal Engineering Conference,1971,3(1): 1537-1556.

[8] HATTORI M. Wave transmission from horizontal perforated plates[C]//Proceedings of the 22nd Conference on Coastal Engineering. New York: ASCE,1975: 513-517.

[9] SIEW P F,HURLEY D G. Long surface waves incident on a submerged horizontal plate[J].Journal of Fluid Mechanics,1977,83(1): 141-151.

[10] BROSSARD J,CHAGDALI M. Experimental investigation of the harmonic generation by waves over a submerged plate[J]. Coastal Engineering,2000,42(4): 277-290.

[11] RAO S,SHIRLAL K G,VARGHESE R V,et al. Physical model studies on wave transmission of a submerged inclined plate breakwater[J]. Ocean Engineering,2009,36(15): 1199-1207.

[12] 刘丹.波浪对两层潜式水平板的作用研究[D].大连: 大连理工大学,2011.

[13] BURKE J E. Scattering of surface waves on an infinitely deep fluid[J]. Journal of Mathematical Physics,1964,5(6): 805-819.

[14] PATARAPANICH M. Maximum and zero reflection from submerged plate[J]. Journal of Waterway,Port,Coastal,and Ocean Engineering,1984,110 (2): 171-181.

[15] NALLAYARASU S,CHEONG H F,SHANKAR N J. Wave induced pressures and forces on a fixed submerged inclined plate [J]. Finite Elements in Analysis and Design,1994,18(1): 289-299.

[16] 王科.潜式水平板型防波堤消浪效果研究[D].大连: 大连理工大学,2001.

[17] LEE M M,CHWANG A T. Scattering and radiation of water waves by permeable barriers[J]. Physics of Fluids,2000,12(1): 54-65.

[18] ISAACSON M,PREMASIRI S,YANG G. Wave interactions with vertical slotted barrier[J]. Journal of Waterway,Port,Coastal,and Ocean Engineering,1998,124(3): 118-126.

[19] 俞聿修.随机波浪及其工程应用[M]. 大连: 大连理工大学出版社,2000.

Experimental study on wave-damping performance of porous inclined plate//

WANG Guoyu, ZHAO Weijiao, XIANG Zhuqing, ZHU Gancheng

(StateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian116024,China)

The wave-damping performance of a single perforated and inclined plate was explored through physical model tests under two-dimensional regular waves. In the tests, the plate is installed with angles of 15° and -15°, and porosity ratios of 0%, 10%, 20%, and 30%, respectively. The variation of the reflection, transmission, and energy dissipation coefficients with the relative width (the ratio of plate width to wave length) are also presented. The results demonstrate that an inclined plate with an angle of 15° can dissipate more energy than that with an angle of -15°. The relative width and the porosity ratio both influence the wave-damping performance.

plate; porosity ratio; wave; wave-damping; model test

中央高校基本科研业务费专项(DUT15TD42)

王国玉(1977—),男,副教授,博士,主要从事海岸工程研究。E-mail:wanggyu@dlut.edu.cn

10.3880/j.issn.1006-7647.2017.01.004

O353.2

A

1006-7647(2017)01-0022-05

2015-11-20 编辑：骆 超)