电力系统用三相UPS的逆变器控制策略研究
2017-01-12刘国瑞
刘国瑞
(国网山西省电力公司调度控制中心,山西 太原 030001)
电力系统用三相UPS的逆变器控制策略研究
刘国瑞
(国网山西省电力公司调度控制中心,山西 太原 030001)
逆变器作为电力系统UPS(Uninterruptible Power Supply)的输出端,直接向调度自动化系统、变电站远动通讯装置、故障信息子站等提供高质量、高可靠性的交流净化电源。针对传统逆变器存在的输出电压波形质量差,直流电压利用率低,谐波含有率高等问题,建立了三相PWM逆变器在三相静止坐标系和两相旋转坐标系下的数学模型。研究了其基于电压空间矢量和电压电流双闭环控制的逆变器控制策略,并在Matlab的Simulink中进行了系统仿真。仿真结果表明,控制策略合理,满足电力系统用UPS要求。
逆变器;脉宽调制;解耦控制;空间矢量
0 引言
伴随着电力系统自动化、智能化程度的不断提高,UPS(Uninterruptible Power Supply) 在电力调度通信自动化设备、变电站远动通讯装置、图形网关机、继电保护故障信息子站等系统中的应用越来越广泛,其输出电压的品质已成为影响电力调度和变电站通讯自动化系统安全稳定运行的关键因素。逆变器作为电力系统UPS的输出端,是整个UPS系统的核心,传统的三相逆变器大多采用基于三角载波控制的对称规则采样或不对称规则采样进行控制,对称规则采样法输出电压波形谐波含量非常高,不对称规则采样虽然使电压输出波形得到了一定程度的改善,但其对直流电压母线利用率偏低,且在带整流型负载和非线性负载时动态调节慢、输出电压波形严重畸变。本文针对传统逆变器存在的问题,建立了三相PWM逆变器在三相静止坐标系和两相旋转坐标系下的数学模型,研究了其基于电压空间矢量和电压电流双闭环控制的逆变器控制策略,并在Matlab的Simulink中进行了系统仿真。仿真结果表明,控制策略合理,满足电力系统用UPS要求[1,2]。
1 三相PWM逆变器的数学模型及双闭环PI控制策略
1.1 三相静止坐标系下的数学模型
分析数学模型是理论研究和设计的出发点和基础,建立三相电压型桥式逆变器的数学模型,是分析和研究三相PWM逆变系统的基础。逆变器的开关模型可以准确模拟其在不同负载条件下的瞬态时域模型,其缺点是开关非线性,工程上通常利用状态空间平均法建立线性模型,研究其频域转换特性。图1是三相逆变电源主电路,由三相逆变桥、三相滤波器组成。假定三相滤波器对称、一致,滤波电感为L1,滤波电容为C1,而R0代表电感损耗、线路阻抗及开关开通和关断损耗的总效应。
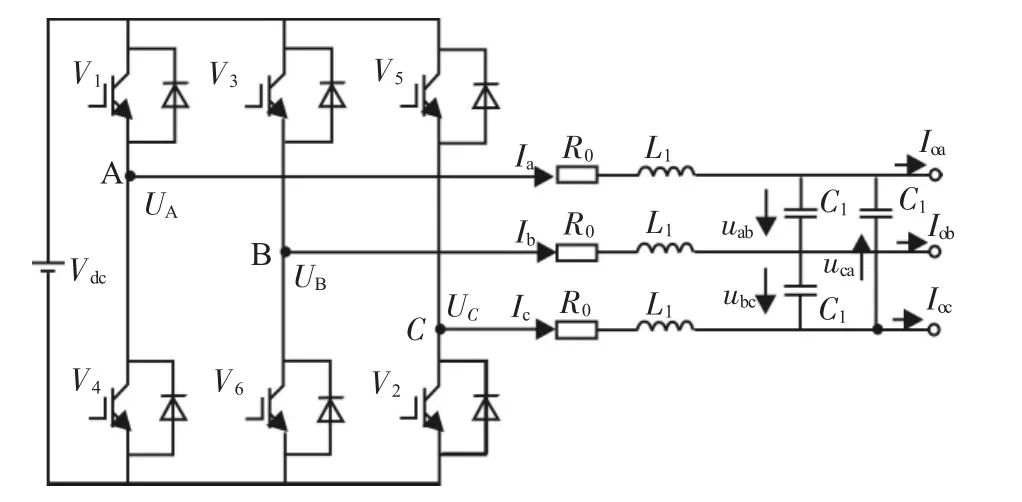
图1 三相逆变电源主电路
根据图1可得三相逆变器在三相abc静止坐标系下的状态空间平均模型。

1.2 两相旋转坐标下的数学模型
三相静止坐标系下的状态空间平均模型是一个多输入、多输出、强耦合的控制对象,其交流侧是随时间变化的交流量,控制系统设计相当复杂。采用坐标变换,建立三相逆变器,在以电网基波频率同步旋转的dq坐标系下的数学模型如下。

从式(2)和式(3)可看出,经过坐标变换,逆变器已由多输入、多输出简化为两输入、两输出,但该模型输入输出之间仍存在耦合。
1.3 dq坐标系下的解耦控制策略
在dq旋转坐标系下,4个状态变量ud、Id、up、Iq相互耦合,不利于控制器设计,经过解耦后方能单独控制ud、Id、uq、Iq。
根据图1所示的三相PWM逆变器的电路结构,由基尔霍夫KVL、KCL可得
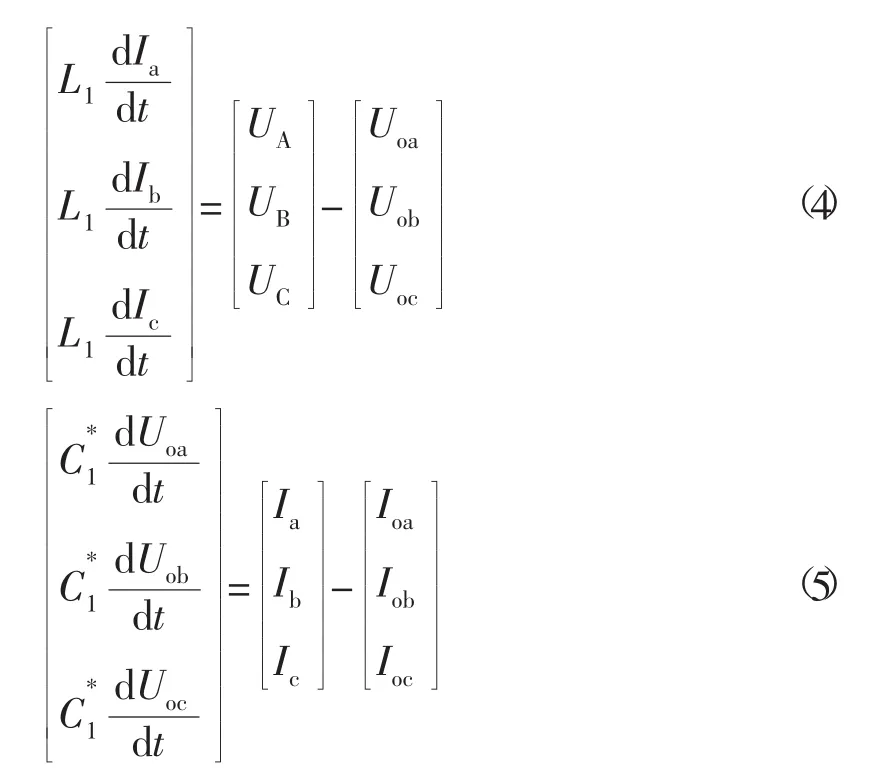

由式(6)—(9)可以构成图2所示的电压电流双环解耦控制系统。

图2 逆变器系统解耦控制框图
式(8)与(9) 构成电流内环反馈控制器,其输出为外环,由式(6)与(7)构成的电压控制器和输出电压反馈构成电压外环,在电压外环的作用下实现对输出电压的稳定控制。式(8)与(9)构成的电流控制器与输出电流反馈构成电流内环,其输出作为外环的给定。此外,整个系统通过引入负载电流和输出电压前馈,提高了调节器控制精度和系统响应速度,使逆变器抗干扰和承受非线性负载的能力进一步得到加强。利用输出电压空间矢量ud和uq,在电压空间矢量SVPWM控制技术的调节下,得到逆变器6个开关器件的PWM驱动信号,从而使得逆变器在电压电流双环控制下,输出额定正弦波电压。
2 空间矢量PWM控制技术
2.1 电网电压和参考电压空间矢量
设电网电压为三相对称电压。

电网电压和参考电压在空间矢量控制系统中定义如下。
a)电网电压空间矢量。
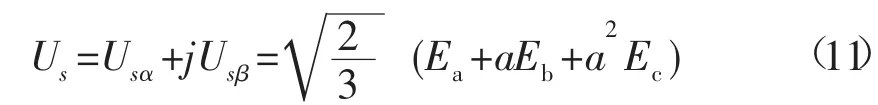
式(11)中,电网电压空间矢量在两相静止坐标系中被分解为Usα、Usβ, a=ei2π/3。
b)参考电压空间矢量。

式(12)中,参考电压空间矢量Uref在两相静止坐标系中被分解为Urα、Urβ,a=ei2π/3。
2.2 电压空间矢量计算的简化
图3为空间电压矢量分布图。

图3 空间电压矢量分布图
根据Uref在α、β轴上的坐标值Urα、Urβ可以计算出Uref与α轴夹角γ的正切值,,通过反正切函数即可求得γ,进而确定空间矢量的作用时间T1、T2。此计算方法理论简单,容易理解,但由于反正切函数计算复杂,CPU频率达到72 MHz才能勉强满足控制要求,下面介绍一种工程上常用的简单算法,根据参考电压来判断所属扇区和作用时间。
a)矢量的作用时间。
由图3可知,参考电压矢量Uref可由它所在扇区的2个空间矢量及零矢量合成得出,因此通过参考电压矢量Uref可计算出6个空间矢量在各扇区的作用时间,以Uref在图3所示的第I扇区为例。

式中,Ts为CPU采样周期,为直流侧电压矢量。
根据式(13) 和(14),可以算出V4(100)和V6(110) 在一个控制周期内的作用时间T1和T2,在其余各扇区内均有此类似关系。
零矢量的作用时间为T0=Ts-T1-T2。
b)扇区的选择。
根据参考电压矢量Uref及其在α、β坐标系的分量Urα、Urβ,定义

若X>0,则A=1,否则A=0;
Y>0,则B=1,否则B=0;
Z>0,则C=1,否则C=0。
则控制过程中可通过N=A+2B+4C来判断参考电压空间矢量属于哪一个扇区。
c)开关矢量的合成。
工程上为最大限度减少开关损耗,逆变器调制过程中每次仅允许切换1只开关管,七段空间矢量合成方法可满足次要求,即每个矢量控制以(000)开始和结束,中间加以矢量(111),这样就可以保证每次只切换1只开关管。表1为各扇区开关矢量分配表。图4为第I扇区内空间矢量作用时间图。

表1 各扇区开关矢量分配表
通过以上分析可知,此方法首先计算判断参考电压所属扇区,然后通过各扇区开关矢量分配表得知开关管切换顺序,再计算矢量作用时间后即可合成参考电压空间矢量,整个过程不涉及复杂计算,控制简单,且非常易于数字化CPU实现[3-5]。

图4 第I扇区内空间矢量作用时间图
3 系统仿真
图5为基于空间矢量控制和电压电流双闭环控制策略的三相电压型PWM逆变器仿真系统模型图。系统的部分仿真参数为:输出滤波电感0.4 mH,输出滤波电容100μF,输出电阻忽略不计,输出负载容量4 kVA,开关频率20 kHz,采用可变步长ode23tb,仿真时间为0.1 s。图6—图9所示为逆变器仿真模型在负载功率因数为0.8,输入直流电压380 V的情况下系统的仿真结果图。
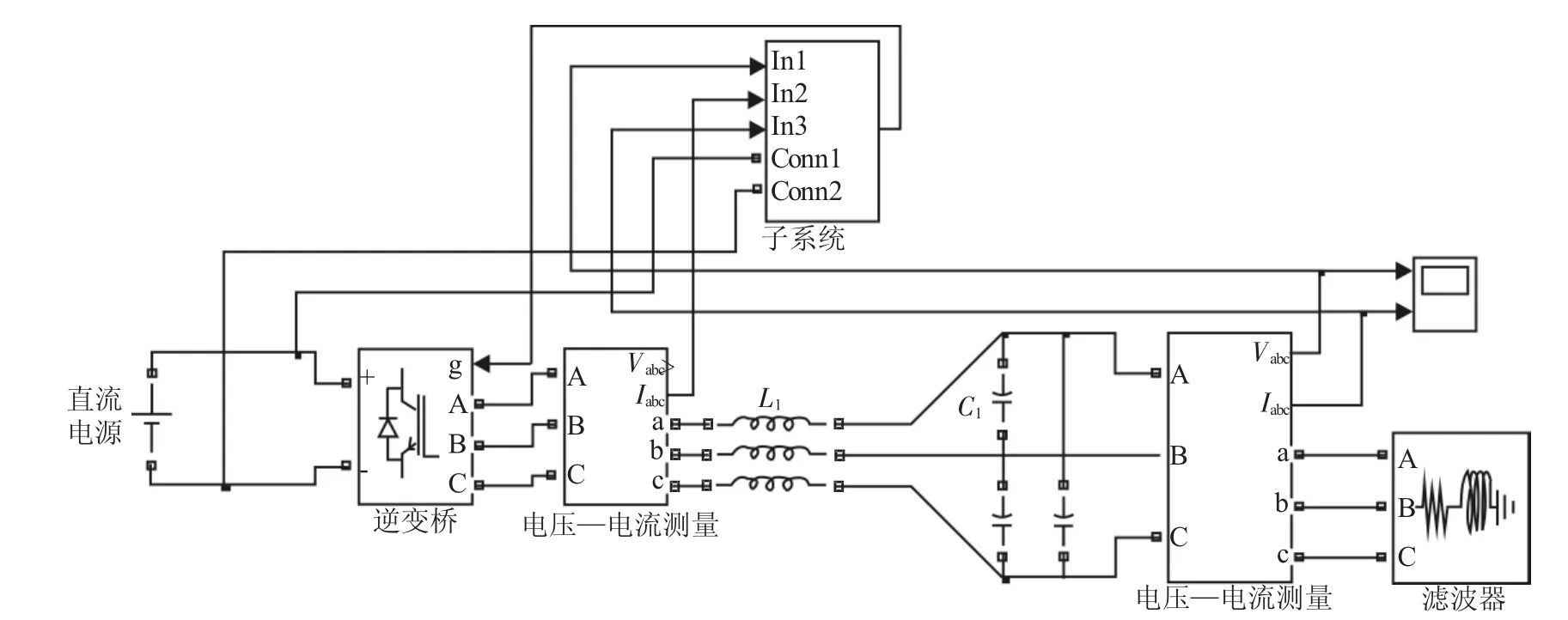
图5 三相电压型PWM逆变器仿真模型图
4 仿真分析
由图6可知,三相输出电压波形对称且相差1 200 V,且通过Simulink中的RMS模块可测得,稳态时A相电压有效值为126.4 V。由图7可知,三相输出电流波形在感性负载时仍然对称,且未发生畸变,通过Simulink中的RMS模块可测得,稳态时A相电压有效值为10.44 A。由图8可知,逆变器在带感性负载时,电压波形和电流波形和负载性质相同,功率因数为0.8。由图9可知,逆变器在感性负载时,电压波形畸变率很低,其总谐波含有率仅有1.23%,低于国标规定的5%。由图6—图9可以看出,采用基于电压空间矢量控制和电压电流双闭环的逆变器控制策略,达到了预期的控制效果,电压电流波形对称,畸变率低,谐波含有率低,负载适应能力强[6]。

图6 输出三相相电压波形图
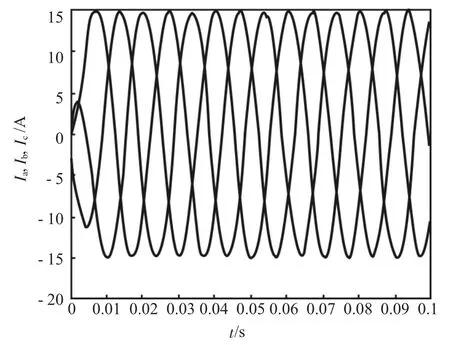
图7 输出三相相电流波形图

图8 输出A相电压电流波形图

图9 A相输出电压总谐波畸变图
5 结束语
本章深入研究了三相逆变器的拓扑结构,确定了将三相桥式逆变器作为主要研究对象。针对三相桥式逆变器的拓扑结构,建立了三相电压型PWM逆变器在各种坐标系下的数学模型,选择了基于电压空间矢量PWM的电压电流双闭环控制方式,给出了逆变器系统的解耦控制框图,最后在Matlab/ Simulink中对逆变器仿真模型进行了仿真。仿真结果对实际应用有较强的借鉴意义。
a)设计方法可行,控制策略选取合理,仿真模型建立正确。
b)逆变器输出功率因数范围宽,输入直流母线电压范围宽,输出电压电流精度高,输出电压电流的THD低。
[1]Jacobina C B,Lima A M N,Da Silva E R C.Digital scalar pulse-width modulation: A simple approach to introduce non-sinusoidal modulation waveforms[J].IEEE Transactions on Power Electronics,2001,16(3):351-359.
[2]A Tuladhar,H Jin,T Uger,et al.Control of Parallel Inverters in Distributed AC Power Systems with Consideration of the Line Impedance Effect[J].IEEE APEC'98,1998(1):321-328.
[3]谢力华,苏彦民.正弦波逆变电源的数字控制技术[J].电力电子技术,2001(6):52-55.
[4]袁泽剑,钟彦儒,杨耕,等.基于空间电压矢量技术的最小开关损耗PWM技术[J].电力电子技术,1999(6):12-15.
[5]张兴,张崇巍.PWM可逆变流器空间电压矢量控制技术的研究[J].中国电机工程学报,2001,21(10):102-105.
[6]薛定宇.基于MATLAB/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2002.
Research of PWM Inverter Control Strategy in Three-phase UPS for Power System
LIU Guorui
(State Grid Shanxi Electric Power Corporation,Dispatching&Control Center, Taiyuan,Shanxi 030001,China)
As the UPS output terminal, inverter directly supplies purified AC power source with high quality and high reliability for power dispatching automation system, substation RTU and relay protection fault information subsystem. In order to improve the wave form quality, utilization efficiency of DC voltage, and decrease total harmonic distortion, a three- phase PWM inverter mathematical model is established in the three- phase stationary coordinate system and two- phase rotating coordinate system in this paper. In addition, the control strategy based on voltage space vector and voltage- current dual- loop control is studied, and it is simulated under Matlab/Simulink. The simulating result has proved that the control strategy is practicable and reasonable, and it can meet the requirement for UPS in power system.
inverter;PWM;decoupling control;space vector
TM464
A
1671-0320(2016)02-0018-05
2015-12-10,
2016-01-20
刘国瑞(1984),男,山西运城人,2010年毕业于太原理工大学电气工程及其自动化工业,硕士,工程师,研究方向为电力系统及其自动化。
