CO2驱注采井网流线分布规律研究

吕玉丽, 廖新维, 李蒙蒙

(1.中国石化西北油田分公司 采油二厂, 新疆 轮台县 841604； 2.中国石油大学(北京) 石油工程学院, 北京 102249)

CO2驱注采井网流线分布规律研究

吕玉丽1, 廖新维2, 李蒙蒙2

(1.中国石化西北油田分公司 采油二厂, 新疆 轮台县 841604； 2.中国石油大学(北京) 石油工程学院, 北京 102249)

CO2驱油技术可以有效解决注水开发中的问题，提高油藏采收率.用流线法求解CO2驱组分数值模型可有效解决常规有限差分方法求解过程中计算效率低、数值弥散等问题.本文基于流线方法，建立了不同储层条件和不同井网条件下的CO2驱理论模型，分析了CO2驱注采井网流线分布规律.通过实例，分析了不同生产时间条件下的井网流线分布.结果表明流线分布图能直观描述注采井间的流动关系，流线密集区域一般分布在注入井和生产井的连线附近，说明流动能力强，驱油效果好.流线稀疏区域一般分布在远离注采井的区域或生产井之间的压力等势面上，说明剩余油较多.流线分布规律可为油田开发中后期井网调整提供依据.

二氧化碳驱； 流线法； 注采井网； 流线分布； 实例分析

0 引言

流线法数值模拟技术具有广阔的前景，主要原因在于两个方面：一是对于大规模的非均质油藏描述，流线法的模拟速度远快于传统的有限差分方法[1,2]；二是流线法可以直接计算质点沿着流线的飞行时间，飞行时间的等值线能直观的表征驱替前缘.在油藏数值模拟的基础上，利用流线方法能定量的表征注采井间动态关系[3-5].

Mathews等[6]在1989年应用流线方法模拟了均质多孔介质中的面积流，虽然他们认识到流线位置会随着时间改变，但并没有进一步研究流线追踪的方法.Datta-Gupta等[7]在1995年提出了模拟非均质油藏中质点移动的半解析方法，先由传统的有限差分方法得到速度场，然后再在速度场的基础上用流线法进行求解.Crane等[8]在2000年建立了全组分流线模型，给出了具体的求解步骤，并与传统的有限差分方法进行比较，指出流线模型的快速高效优势.Jessen等[9]在2004年建立了考虑重力分异的全组分流线模型，运用算子劈分技术，分别沿着流线和重力线对饱和度方程进行求解.Osako等[10]在2007年建立了考虑弹性影响因素的全组分流线模型，引入“体积平衡”的概念对模型进行求解.2010年，Sayyafzadeh等[11]应用流线密度来表征油藏流体的流动，并根据油藏流体分布规律提出井网加密或者油井转注等调整措施.2011年，Kang等[12]通过研究气井生产区域的流线分布，对天然裂缝致密气藏中井的位置进行了优化.

国内应用流线法进行CO2驱数值模拟的研究起步较晚[13-15]，目前国内还没有基于流线法的数值模拟软件，需要进一步探讨和研究.本文在前人研究基础上，应用流线法对建立的CO2驱组分数值模型进行求解，并分析了不同储层、不同井网及不同生产时间条件下的井网流线分布规律，为油田开发中后期生产调整提供理论依据.

1 CO2驱油理论模型

为了研究注采流线在不同的井网、不同均质程度的地层中的分布规律，分别设计了均质和非均质两种地层条件下的不同井网模型，进行CO2驱流线法组分模型数值模拟.所建理论模型为一个网格系统为横向11个网格、纵向11个网格(即11×11)的二维平面模型，x方向和y方向的渗透率均为2 mD，孔隙度为0.2，原始地层压力为20 MPa，原始含油饱和度为0.5，含水饱和度为0.42，含气饱和度为0.08.x和y方向的网格长度为50 m，z方向的网格长度为2 m.储层流体的相渗数据见表1和表2所示.

表1 油水相渗数据

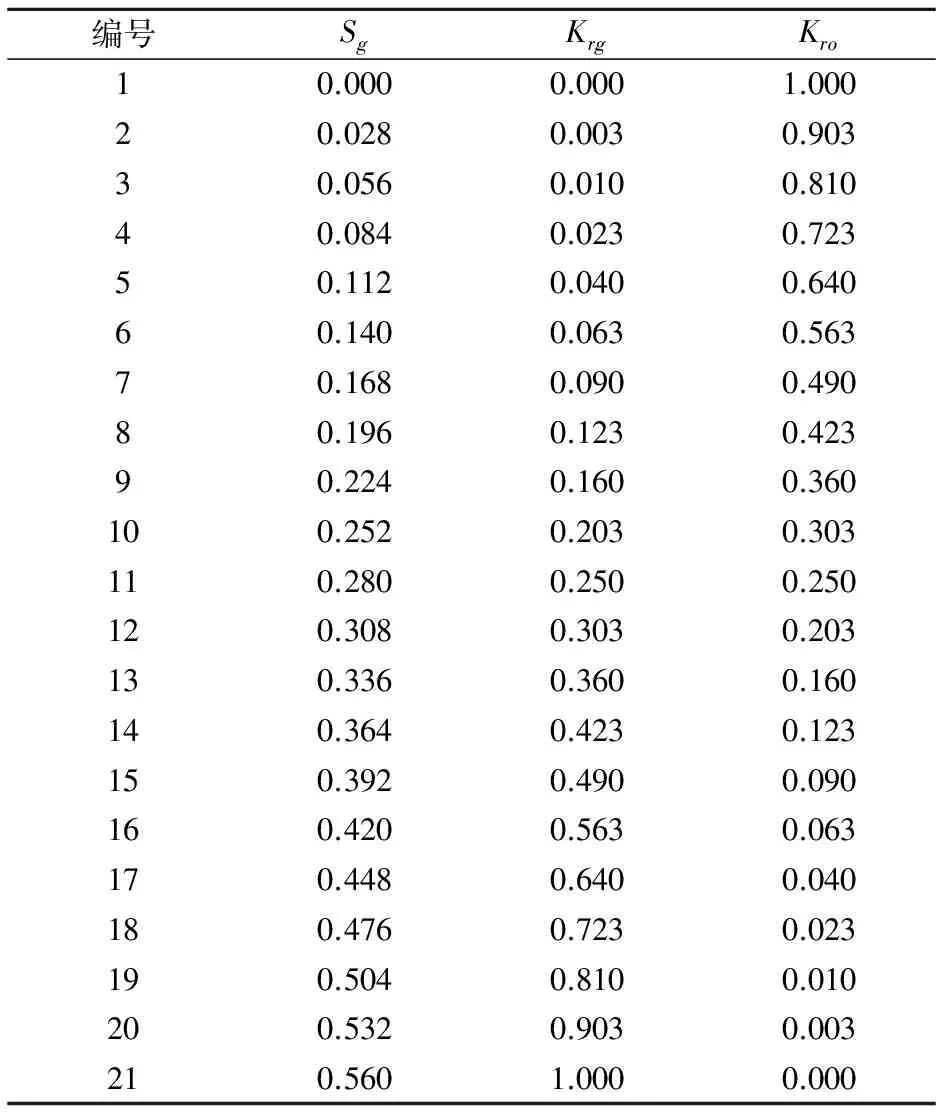
表2 油气相渗数据

根据油水、油气两相相渗数据，采用Stone三相模型预测了三相体系中的油相相对渗透率.

归一化饱和度可表示为：

(1)

其中，Sw≥Siw，且

(2)

其中，So≥Sor，且

(3)

那么，有

(4)

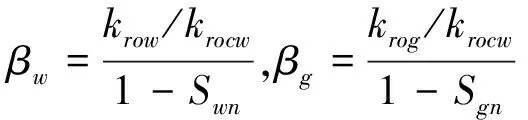
式中：Swn为三相体系中归一化含水饱和度；Sw为含水饱和度；Siw为束缚水饱和度；Sor为残余油饱和度；Son为三相体系中归一化含油饱和度；So为含油饱和度；Sgn为三相体系中归一化含气饱和度；Sg为含气饱和度；krw为水相相对渗透率；kro为油相相对渗透率；krg为气相相对渗透率；krow为油水两相中水相相对渗透率；krog为油气两相中气相相对渗透率.

2 注采井网流线分布规律研究

2.1 均质地层井网流线分布

在均质地层模型中选用五点法、七点法、九点法以及反七点法井网进行流线法CO2驱组分数值模拟研究，并根据现场的实际生产制度给出各井的控制条件，分析评价不同井网条件下的流线分布规律.

(1)五点法井网的注采流线分布规律

在该井网中，设有五口虚拟井，其中四个角上为生产井，中间为注气井.生产井控制条件为定井底流压(5 MPa)生产，注气井为定注入量(12 t/d)，流线条数为100条.

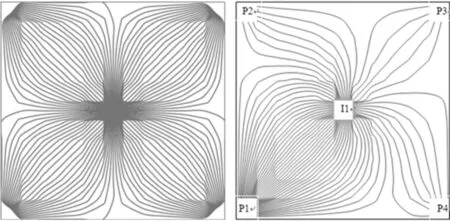
(a)相同井底流压条件 (b)不同井底流压条件图1 不同条件下井网流线分布图

图1(a)表示生产井井底压力相同时流线分布特征.从图1(a)可以看出，每个1/4区域流线分布都对称，每个区域流线条数为25条.流线分布密集的区域为注入井和生产井的连线附近，即主流线方向.而在各生产井之间的压力等势面上流线分布稀疏，说明流经此区域的注入气流量较小，驱油效果不好，剩余油饱和度较高.在模拟过程中，当生产制度或井网分布不改变时，流线分布不会发生明显变化.因此，减少了频繁的更新流线，节省了模拟时间.

由于每口生产井的井底流压控制条件都是相同的，所以4个区域的流线分布也是完全对称的，如果将每口生产井的井底流压分别设为3 MPa、8 MPa、10 MPa、8 MPa，得到新的流线分布如图1(b)所示，图1(b)表示生产井井底压力不相同时的流线分布特征.此时流线在每个1/4区域里分布明显不均匀，这是由每口井的控制条件不同造成的.由于每条流线都代表一个相等的流量，所以流线疏密程度就可以表示该区域流量的大小，可以通过简单的统计流线条数来定量的分析每口生产井的受效情况.在图1(b)中，注入井I1流入生产井P1的流线为41条，流入生产井P2的流线为7条，流入生产井P3的流线为5条，流入生产井P4的流线为7条.其中，生产井P2和P4井底流压控制条件都为8 MPa，所以流入P2和P4的流线条数也相等.这样就能直观地看到注入井对生产井的贡献，定量分析生产井的受效情况.通过与图1(a)的对比，说明生产制度的改变会引起流线形态发生变化，所以，当生产制度变化时要更新流线.

(2)七点法井网的注采流线分布规律

七点法井网分为正七点和反七点两种井网，在正七点井网中，设有七口虚拟井，其中六口为注入井，中间一口为生产井，生产井控制条件为定井底流压(10 MPa)，每口注气井都为定注入量(2t/d).在反七点井网中，设有七口虚拟井，其中六口为生产井，中间一口为注入井，每口生产井控制条件为定井底流压(3 MPa)，注气井为定注入量(12 t/d).流线都是由注入井开始追踪到生产井结束.

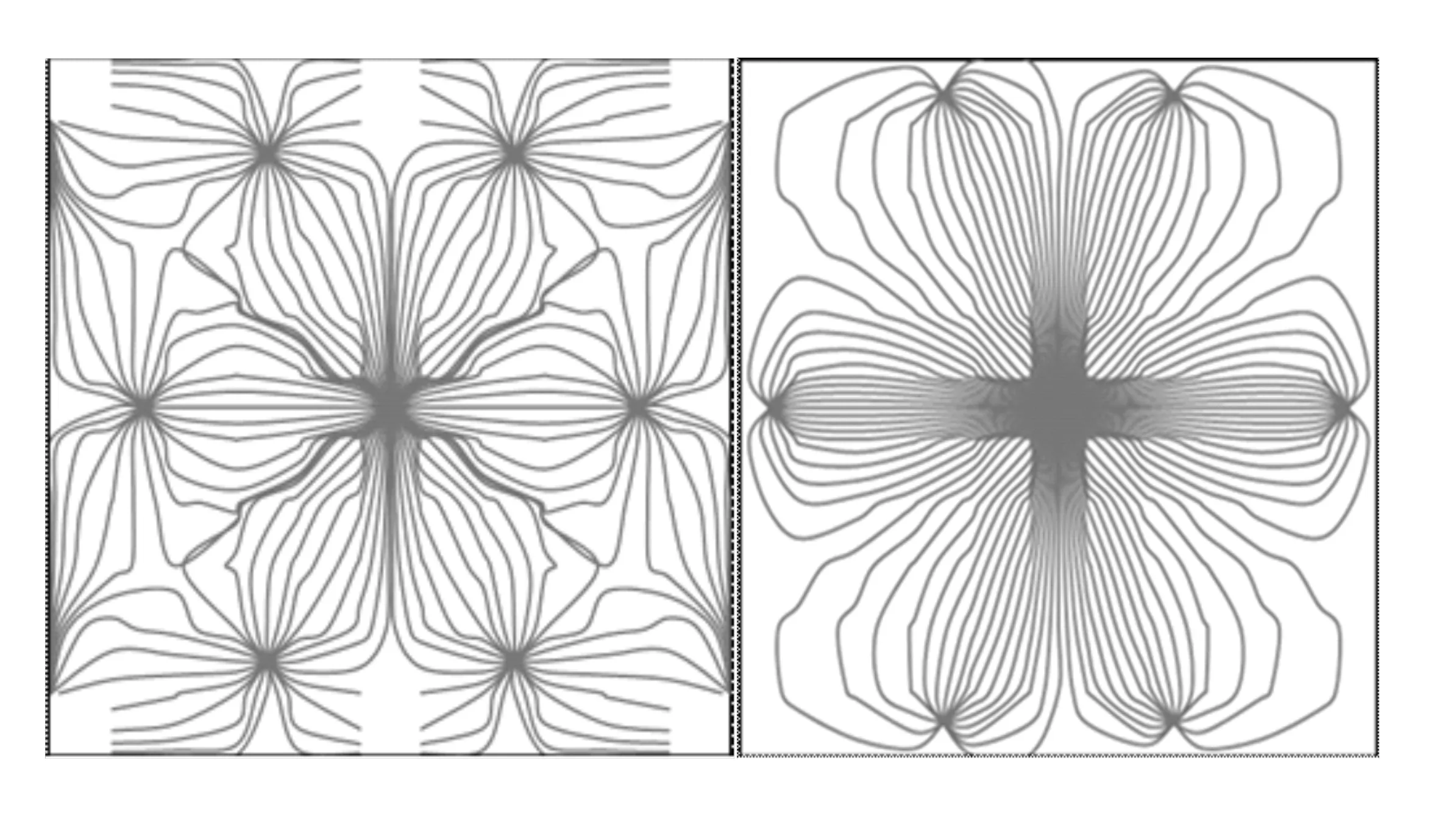
(a)正七点流线分布图 (b)反七点流线分布图图2 七点法井网流线分布图

图2(a)表示正七点井网流线分布.由图2(a)可以看出，正七点井网的注采流线更为复杂，流线密集的地方为中央六边形区域，说明此区域气驱效果较好，剩余油饱和度小.同样，在各注入井压力等势面上，流线稀疏，注入气波及程度较低，剩余油饱和度较大.图2(b)表示反七点井网流线分布.由图2(b)可以看出，流线密集的区域在生产井和注入井的连线上，在四个角上和各生产井等势线上，注入气波及程度较低，剩余油饱和度较高.

(3)九点法井网的注采流线分布规律

以常用的反九点法井网为例，在反九点井网中，设有九口虚拟井，其中八口为生产井，中间一口为注入井，生产井控制条件为定井底流压(2 MPa)，每口注气井为定注入量(12 t/d).

图3表示反九点井网流线分布.由图3可以看出，在反九点法井网中，由于处于中间的注气井离垂直方向上的生产井近，所以注气井的气驱前缘首先到达垂直方向上的四口生产井，四个角上的生产井见气时间较晚.同样，在各生产井压力等势面上，流线条数稀疏，注入气波及程度较低，剩余油饱和度较大.

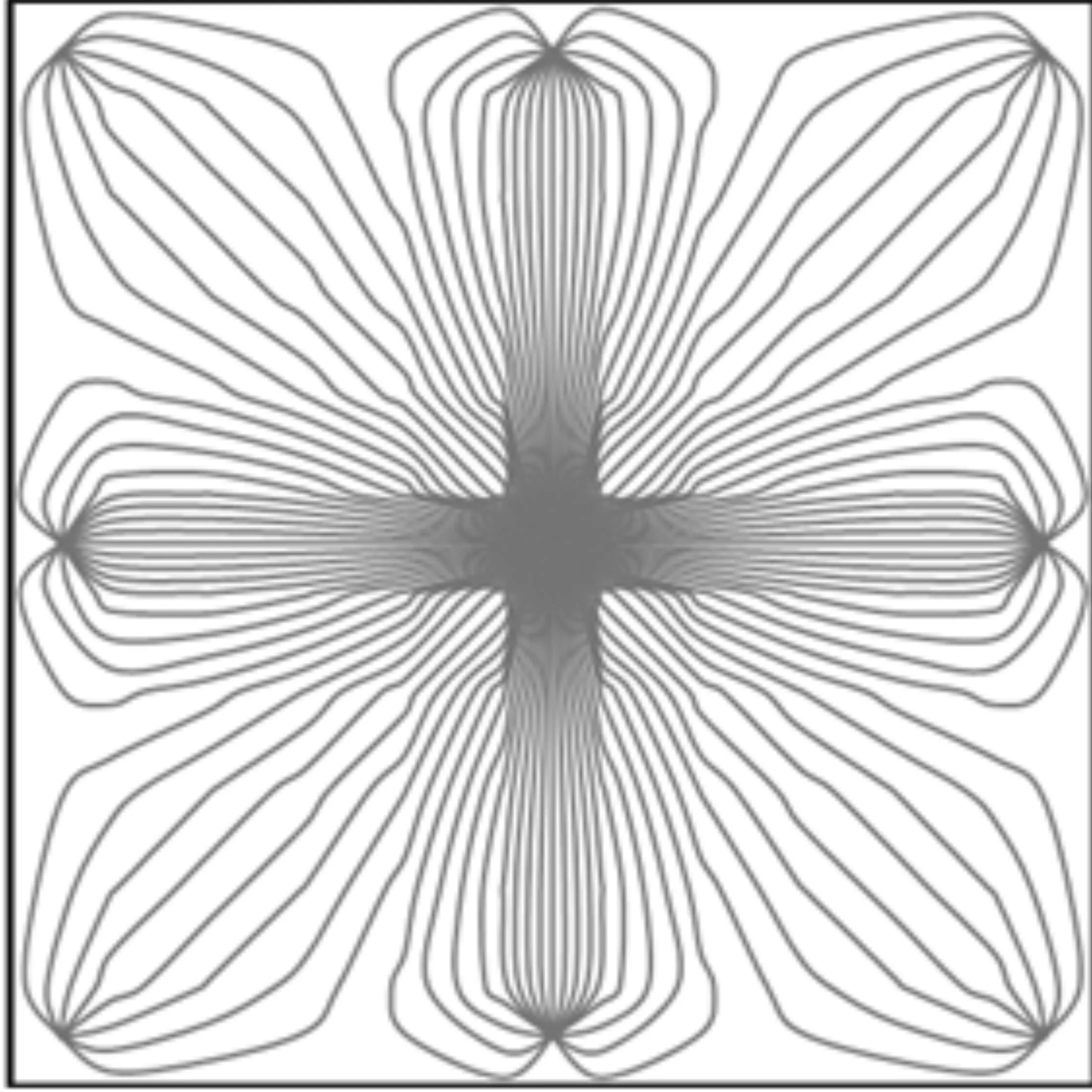
图3 反九点井网流线分布图

2.2 非均质地层井网流线分布

非均质性一般分为平面非均质性和纵向非均质性.平面非均质性主要是受沉积相和成岩作用的控制，由砂体的形态、规模、连续性、渗透率和孔隙度的平面变化引起的.在二维平面上，储层宏观非均质性主要体现在平面非均质性，下面主要考虑渗透率的平面非均质性对流线分布的影响.分别建立x方向渗透率非均质和y方向渗透率非均质的地质模型，以五点法井网作为目标井网，给定井网中各井的控制条件，研究平面非均质性对井网流线分布的影响.

图4(a)表示沿x轴方向的非均质储层的流线分布，图4(b)表示沿y轴方向的非均质储层的流线分布.为了验证x方向渗透率非均质性对流线分布的影响，先设所有网格块在y方向渗透率Ky为2 mD.在地层中，x方向渗透率Kx分布如表3所示.由图4(a)可以看出，在模型的左侧区域流线较密集，说明渗透率大的流动区域流线分布密集，而且在近生产井地带x方向上的流线条数远远大于y方向上的流线条数.即x方向的流量要大于y方向上的流量.

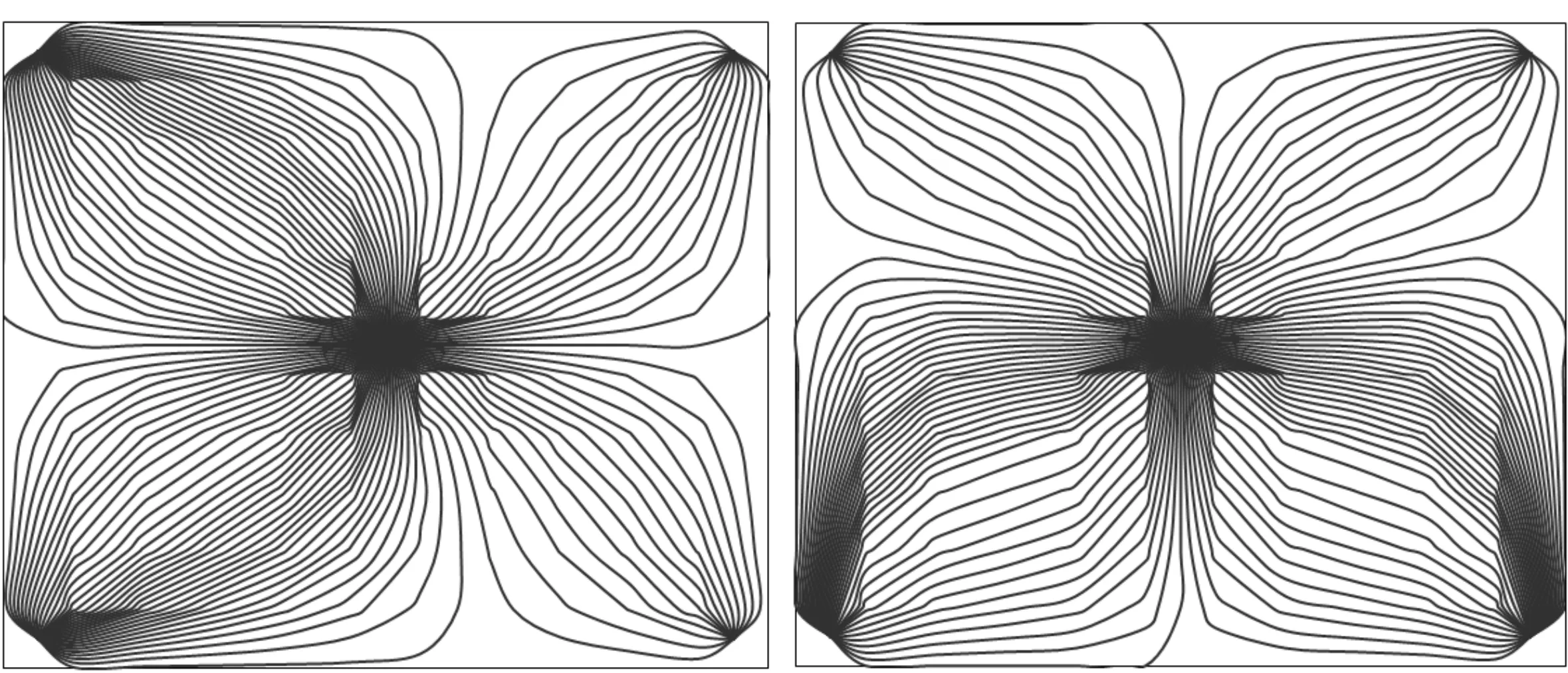
(a)x方向非均质储层 (b)y方向非均质储层图4 非均质储层井网流线分布图

x轴网格点y轴网格点渗透率/mD1⁃661⁃1127⁃112

设在地层中所有网格块在x方向渗透率都为2 mD，在y方向上的渗透率Ky分布如表4所示.由图4(b)可以看出，在模型的下方区域流线较密集，说明下方区域渗透率较大，符合假设条件.同样，在近生产井地带y方向上的流线条数远远大于x方向上的流线条数.即y方向的流量要大于x方向上的流量.

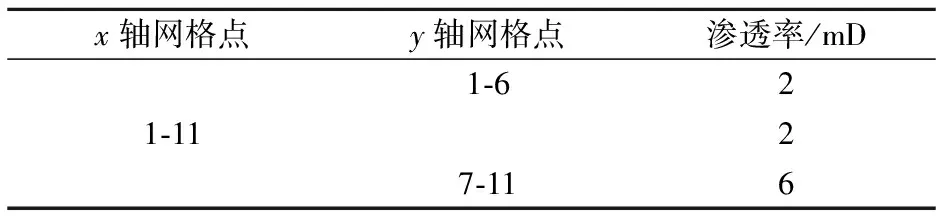
表4 y方向渗透率(Ky)分布

3 油藏实例分析

3.1 区域概况

研究区块是一个略微西倾的白垩纪砂岩油藏，研究区块在开发初期为一次采油阶段.将研究区块划分为图5所示的网格系统，考虑油藏中含有油、气、水三相，存在W1、W2、W3三口井，其中W1为注气井，W2、W3为生产井，所有井均假设无表皮影响，总共的模拟时间为200天.油层平均厚度为6.1 m，地层系数约为4.35×10-4MPa-1.在2 831.6 m参考深度下，初始含油饱和度约为0.5，初始含水饱和度约为0.42，初始含气饱和度约为0.08，原始地层压力约为48.3 MPa.平均有效孔隙度为0.22，渗透率为25 mD.地层脱气原油的压缩系数为7.25×10-4MPa-1，水的压缩系数为4.35×10-4MPa-1.油水和油气相对渗透率曲线如图6所示.

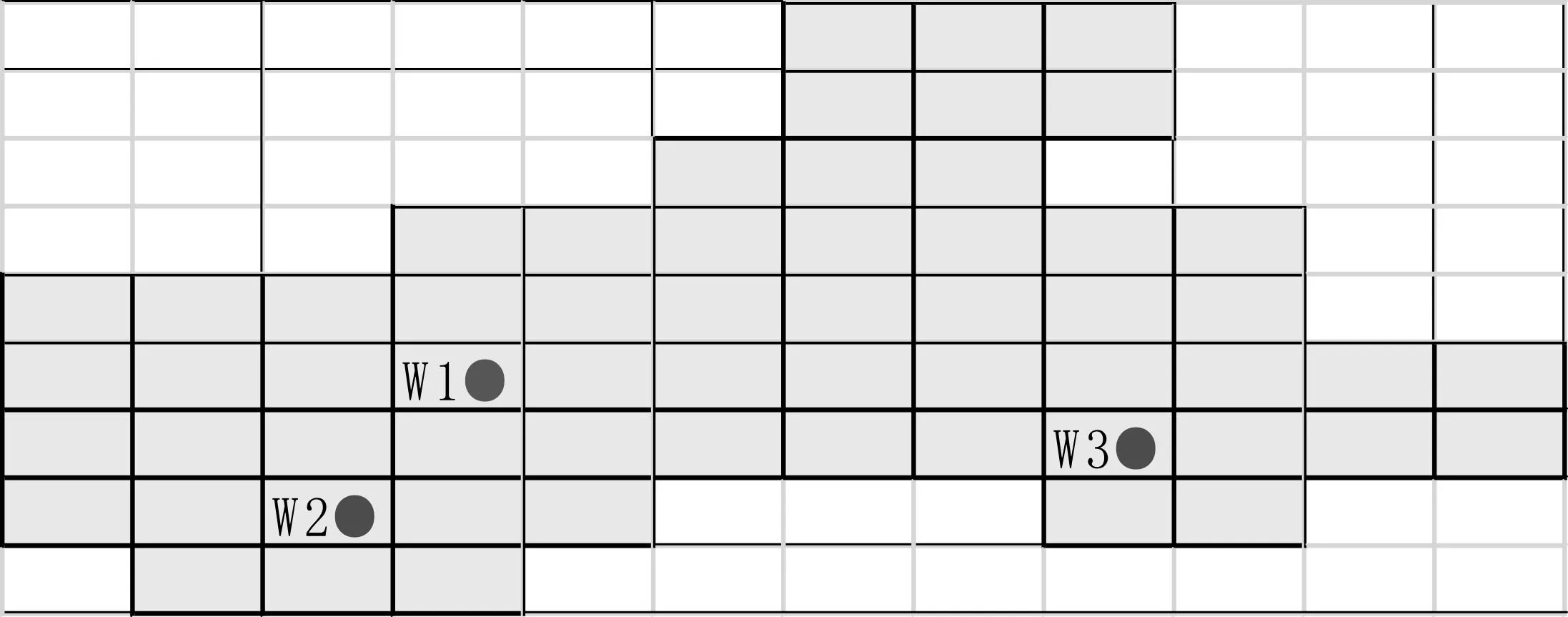
图5 油藏网格划分图

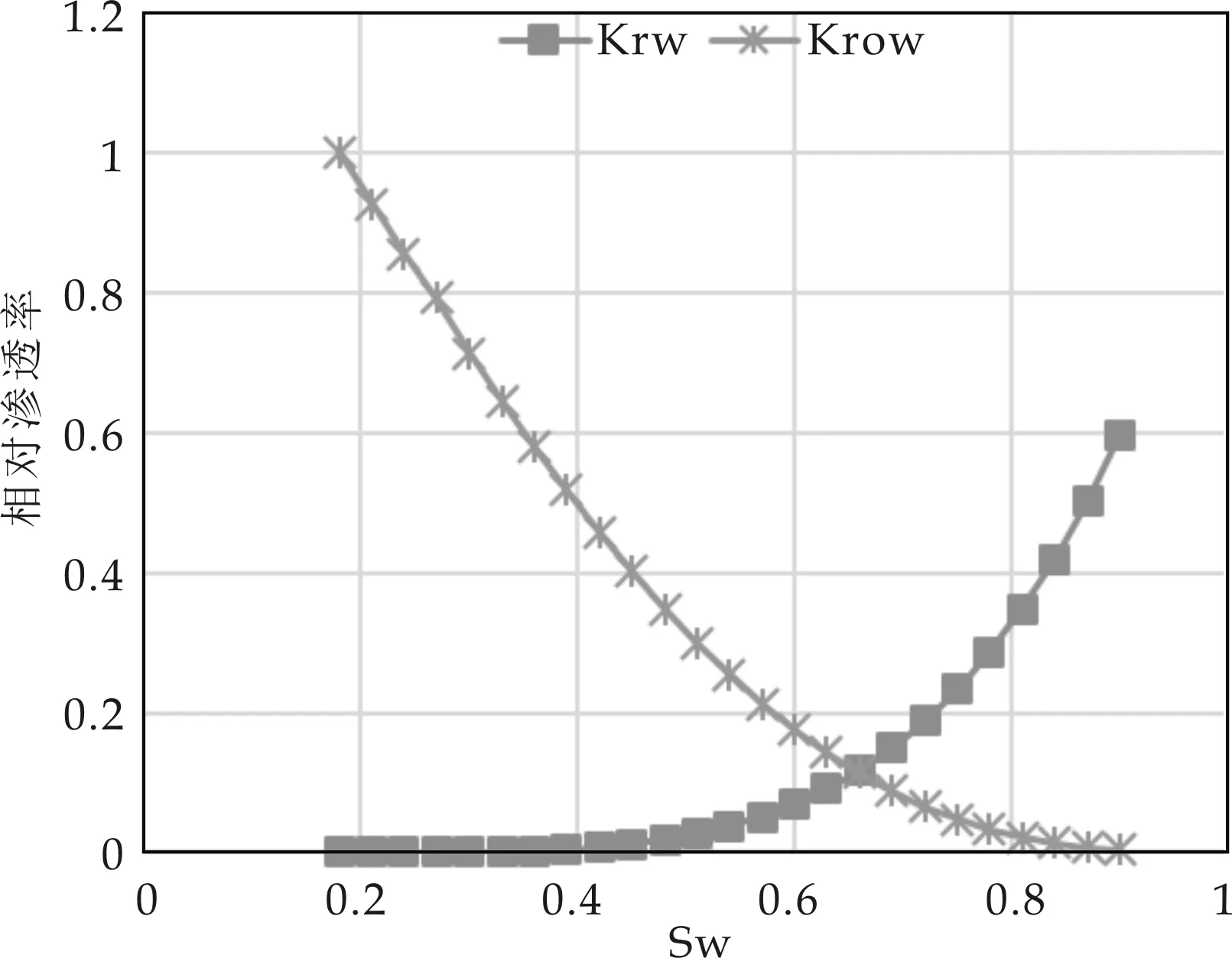
(a)油水相渗曲线

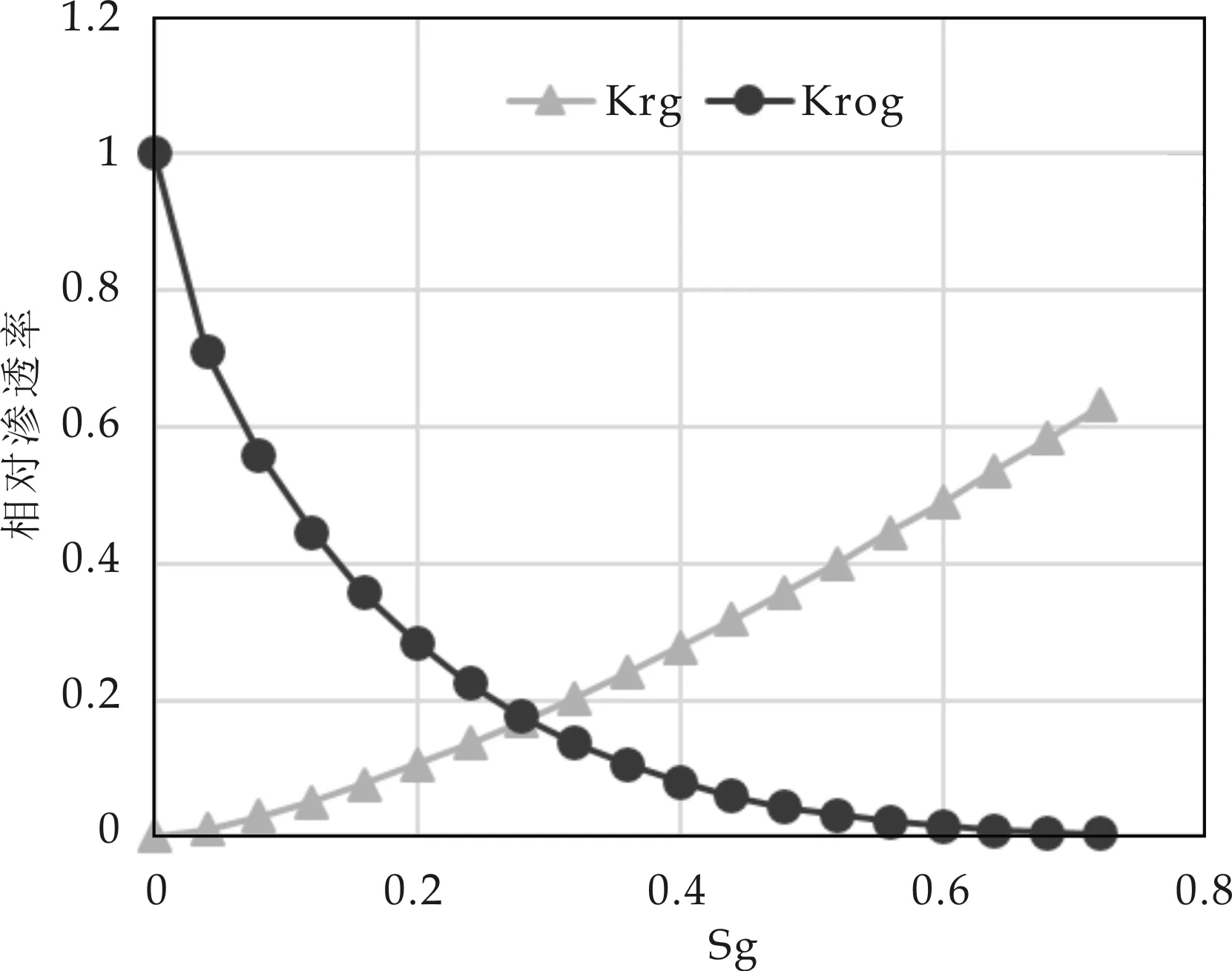
(b)油气相渗曲线图6 油水、油气相渗曲线

3.2 流线法数值模拟结果分析

图7给出了W1、W2、W3三口井分别在模拟时间为10天、100天和200天时的井网流线分布.模拟时间为10天时，在注入井W1周围流线分布比较密集，此时注入气体波及范围较小，仅限于注入井周围区域.注入气体使压力升高，产生压力梯度，发生流体质点的流动，形成流线.模拟时间为100天时，从图7可以看出，流线已经到达W3井，W1井与W2井之间的流线变稀疏，说明流量已经减小，注入井W1由原来只有W2井受效，变为W2和W3井同时受效，但对W2井的贡献明显比W3井要大.模拟时间为200天时，流线分布范围比之前更广，但在地层边界附近流线分布稀疏，在各井之间的连线上流线分布密集，即在井的连线附近，注入气驱油效果较好.

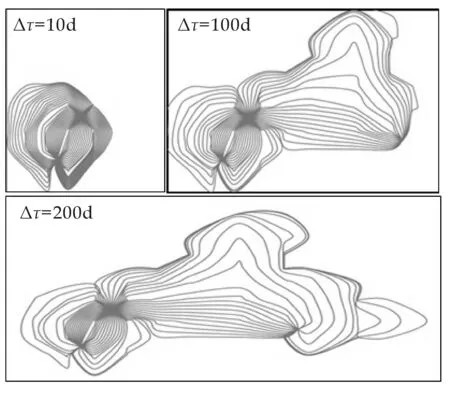
图7 井网流线分布图

在投产初期，流线分布范围会随着生产时间的增加而逐渐增大，在不改变生产制度和井网的前提下，随着生产时间的增加，流线分布最终会达到稳定.在达到稳定形态之后，流线不需要进行频繁更新，迭代循环的时间步可适当加大，不影响计算的精度.

4 结论

(1)采用流线法对建立的CO2驱组分数值模型进行求解，得到了不同储层条件下的井网流线分布规律.设定每条流线都代表一个相等的流量，流线疏密程度代表该区域流量的大小.因此，利用直观的流线分布图，可以定量的描述注采井间的流动关系.

(2)均质地层条件下，流线分布密集的区域为注入井和生产井的连线附近，即主流线方向.而在各生产井之间的压力等势面上流线分布稀疏，剩余油饱和度较高.对于非均质地层，渗透率大的区域，流线分布越密集.在近生产井附近，渗透率大的方向上流线分布越密集，产量越高.

(3)通过对某油藏区块进行实例计算分析，得到该区块不同时间段的流线分布.在投产初期，流线分布范围会逐渐增大，当生产制度不变时，流线分布最终达到稳定.此时可增大时间步，以减少迭代次数，加快计算.

[1] Peddibhotal S.A.,Datta Gupta A.,Wu C.H.Rapid simulation of multiphase flow through fine-scale geostatistical realizations using a new 3D streamline model: a field example[C]//Spe Technical Conference & Exhibition. San Antonio,Texas: Society of Petroleum Engineers,1996:195-218.

[2] Yann Gautier,Martin J.B.,Michael A.C.Nested gridding and streamline-based simulation for fast reservoir performance prediction[J].Computational Geosciences,1999,3(3):295-320.

[3] Thiele M R,Batycky R P,Blunt M J.A streamline-based 3D field-scale compositional reservoir simulator[C]//Spe Technical Conference & Exhibition. San Antonio,Texas: Society of Petroleum Engineers,1997:471-482.

[4] Grinestaff G.H.Waterflood pattern allocations:Quantifying the injector to producer relationship with streamline simulation[C]//Spe Technical Conference & Exhibition. Anchorage, Alaska: Society of Petroleum Engineers,1999:1-5.

[5] Jessen K.,Orr Jr.F.M.Compositional streamline simulation[C]//Spe Technical Conference & Exhibition.San Antonio,Texas:Society of Petroleum Engineers,2002:1-11.

[6] Mathews J.L.,Emanuel A.S.,Edwards K.A.,et al.Fractal methods improve mitsue miscible predictions[J].Journal of Petroleum Technology,1989,41(11):1 136-1 142.

[7] Datta Gupta A.,King M.J.A semianalytic approach to tracer flow modeling in heterogeneous permeable media[J].International Journal of Multiphase Flow,1995,18(1):9-24.

[8] Crane M.,Bratvedt F.,Bratvedt K.,et al.A fully compositional streamline simulator[J].Philosophical Transactions of the Royal Society of London,2000,368(1 631):133-138.

[9] Jessen K.,Orr Jr.F.M.Gravity segregation and compositional streamline simulation[C]//Spe/Doe Symposium on Improved Oil Recovery.Tulsa,Oklahoma:Society of Petroleum Engineers,2004:1-14.

[10] Osako I.,Datta Gupta A.A compositional streamline formulation with compressibility effects[C]//Spe Reservoir Simulation Symposium. Houston,Texas:Society of Petroleum Engineers,2007:1-18.

[11] Sayyafzadeh M.,Pourafshary P.,Rashidi F.Increasing ultimate oil recovery by infill drilling and converting weak production wells to injection wells using streamline simulation[C]//International Oil and Gas Conference and Exhibition.Beijing:Society of Petroleum Engineers,2010:1-7.

[12] Kang S.,Datta Gupta A.,Lee J.Impact of natural fractures in drainage volume calculations and optimal well placement in tight gas reservoirs[J].Journal of Petroleum Science & Engineering,2013,109(9):206-216.

[13] 李培超，曾清红，孔祥言,等.一维混相驱的一种新模型及数值模拟[J].中国科技大学学报,2002,32(6),666-671.

[14] 侯 建.一种基于流线方法的CO2混相驱数学模型[J].应用数学与力学,2004,25(6):635-642.

[15] 郭振宇,王晓东,汤昌福,等.CO2混相驱五点井网流线模拟[J].东北石油大学学报,2012,36(5):88-93.

【责任编辑：蒋亚儒】

Study on streamline distribution of CO2injection-production well pattern

LV Yu-li1, LIAO Xin-wei2, LI Meng-meng2

(1.The 2ndOil Production Plant, SINOPEC Northwest Oil Field Company, Luntai 841604, China; 2.College of Petroleum Engineering, China University of Petroleum (Beijing), Beijing 102249, China)

CO2flooding technology can effectively solve the water injection problems in water flooding and enhance oil recovery.Solving the CO2injection compositional model by streamline method can overcome the problems of poor computational efficiency and numerical dispersion by conventional finite-difference method.The theoretical model of CO2flooding at different reservoir and well pattern conditions were established based on streamline method and the streamline distribution was analyzed.Through instance analysis,the streamline distribution at different production stages was analyzed as well.The results indicate that the streamline distribution map can quantitatively describe the fluid flowing behavior among the injection and production wells.The streamline denser region is distributed near the connecting line between the injection and production wells,which indicates high flow capacity and displacement efficiency.The streamline is sparsely distributed on the pressure equipotential surface of the production wells or the region far from the injection and production wells,which demonstrates a great deal of remaining oil.The streamline distribution can provide beneficial basis for well pattern adjustment in later stage of oil exploitation.

CO2flooding; streamline method; injection-production well pattern; streamline distribution; instance analysis

2016-11-30

国家973计划项目(2011CB707302)； 国家科技重大专项项目(2011ZX05009)

吕玉丽(1985-)，女，山东潍坊人，工程师，硕士，研究方向：油气田开发

1000-5811(2017)01-0114-06

TE341

A