基于自适应滤波的MEMS姿态确定方法

李 鑫，孟翔飞，戴 梅，顾启民

（常熟理工学院，江苏常熟215500）

基于自适应滤波的MEMS姿态确定方法

李 鑫*，孟翔飞，戴 梅，顾启民

（常熟理工学院，江苏常熟215500）

针对消费类电子设备对姿态测量系统的需求，本文提出了一种基于MEMS加速度计、陀螺仪和磁强计的九轴姿态确定算法。针对实际系统中传感器量测噪声未知的情况，首先介绍了一种基于矢量观测器的矩阵Kalman滤波姿态确定算法，然后利用残差匹配技术，设计了一种基于残差匹配的自适应滤波方法。论文采用自适应滤波对传感器量测噪声进行估计，并将估计的量测噪声代入线性矩阵Kalman滤波算法，有效解决了线性矩阵Kalman滤波需要准确量测噪声统计信息的缺陷。最后设计了仿真实验验证本文提出的算法，并将其与线性矩阵Kalman滤波算法比较。仿真结果表明，自适应矩阵Kalman滤波的姿态旋转误差角为0.609 1°，标准差为0.300 9°，能够有效的估计传感器量测噪声，并具有更高的姿态确定精度和稳定性。

姿态确定；自适应滤波；矩阵Kalman滤波；向量观测器

姿态测量是惯性导航的关键技术，其应用场合从航天器到水下航行器，从军事设备到民用消费类电子［1-3］。传统的捷联惯性导航系统均采用高精度的惯性测量传感器进行姿态确定，由于传感器体积大，价格昂贵，不适合民用消费类电子。随着MEMS技术的发展，新型MEMS传感器具有体积小、功耗低，价格便宜等优点，在消费类电子设备中得到了广泛的应用［4-6］。

姿态测量可以直接采用理想陀螺仪测量值计算得到。但是由于传感器存在零偏误差，直接采用陀螺仪测量值，会导致姿态发散，因此需要外部辅助信息对其进行校正。在MEMS系统中，常采用加速度计和磁强计作为观测矢量，设计基于矢量观测器的姿态确定算法，对陀螺仪更新姿态进行校正［7-9］。

常用的MEMS姿态确定方法有基于最优估计理论的非线性Kalman滤波方法以及基于最小二乘理论的K-矩阵方法［10-11］。采用非线性理论的Kalman滤波方法能够在姿态确定的过程中，实时估计陀螺仪零偏，利用估计的陀螺零偏补偿传感器误差，进而得到更高的姿态确定精度［12］。但是，非线性滤波计算量大，收敛速度慢，对实际系统性能要求较高，不利于其在消费类电子中的实现。基于最小二乘理论的K-矩阵Kalman滤波方法是一种线性Kalman滤波姿态确定方法，具有计算简便、滤波效果好的优点［13-14］。由线性Kalman滤波理论可知，在状态估计过程中，往往需要对量测噪声进行准确的噪声特性统计，这限制了线性Kalman滤波的应用范围。在实际系统中，MEMS加速度计与磁强计量测噪声常随温度及地域影响，不易准确得到，若直接使用线性矩阵Kalman滤波，会导致系统滤波精度下降，不利于姿态确定系统稳定可靠运行。针对未知噪声统计滤波，常采用自适应滤波技术，残差匹配自适应滤波具有计算简单的优点，非常适合简易系统应用［15-16］。基于上述分析，本文在现有矩阵Kalman滤波技术的基础上，巧妙地利用了K-矩阵的归一化特性，提出采用残差匹配自适应滤波方法，实现了基于MEMS传感器的姿态确定。

1 系统模型

本节首先介绍一般的矢量观测器模型，并在此基础上介绍基于矢量观测器的K-矩阵模型，最后依据四元数更新方法，给出一般矩阵Kalman滤波模型。

1.1 矢量观测器量测模型

利用导航系下地磁及重力为参考矢量，并考虑磁强计与加速度计均进行了初步校准，在一般MEMS姿态确定中，常用的矢量观测器模型为：

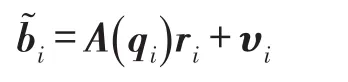
其中，ri∈R3为参考矢量，可通过地磁及重力分布特性准确获取；为观测矢量，可通过磁强计与加速度计测得；υi∈R3为量测噪声；下标i=1,2分别表示磁强计与重力矢量。

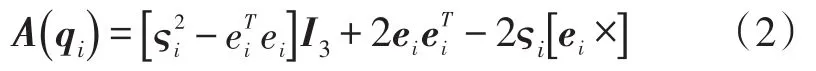
1.2K-矩阵模型

针对磁强计及加速度计的矢量观测模型，可以利用最小二乘方法构造K-矩阵，并通过解析方法得到姿态四元数。常用的基于Wahba问题的K-矩阵模型如下所示：

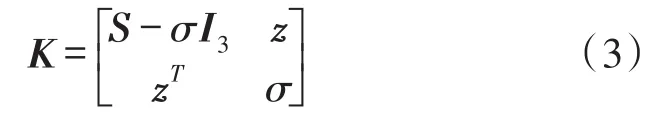
其中，

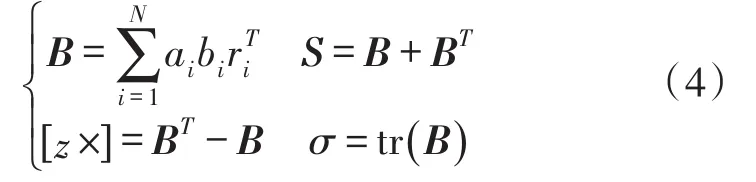
其中，N=2。上式为理想量测矢量bi与参考矢量ri构成的标准K-矩阵，在实际系统中，往往存在量测误差，因此需要利用最优估计理论进行姿态确定。下面考虑含有噪声的观测矢量，并构造基于K-矩阵的矩阵Kalman滤波模型。

1.3 矩阵Kalman滤波模型

根据姿态四元数与K-矩阵之间的传递关系［11］，当观测矢量含有加性随机噪声时，一般的矩阵Kalman滤波模型可以表示为：

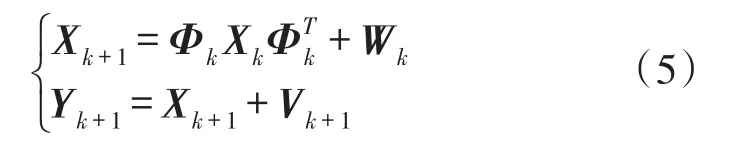
其中，过程噪声为状态相关噪声，即：

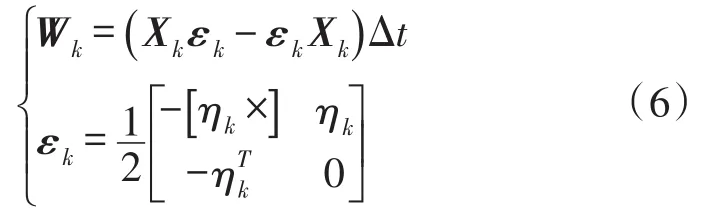
式中，ηk表示陀螺量测随机噪声；Δt表示采样时间。矩阵模型量测噪声主要由观测矢量噪声组成，可表示为：

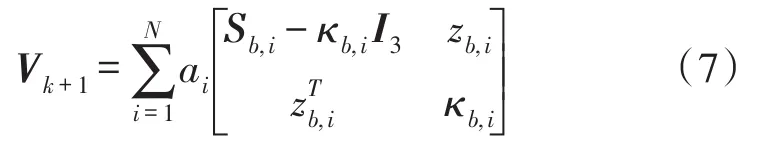
其中，

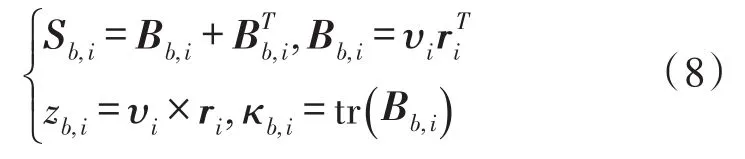
通过上面分析，式（5）中的各未知参量均可由式（6）～式（8）表示，利用式（5）构造的矩阵Kalman滤波模型，设计线性Kalman滤波算法设计，实现K-矩阵的最优估计。

2 自适应矩阵Kalman滤波

基于式（5）一般矩阵Kalman滤波模型，本节首先介绍了线性矩阵Kalman滤波模型，并针对线性矩阵Kalman滤波的缺陷，设计了一种基于残差匹配的自适应矩阵Kalman滤波。

2.1 线性矩阵Kalman滤波

由文献［12］可知，基于K-矩阵模型的线性矩阵Kalman滤波流程如下：

①时间更新：

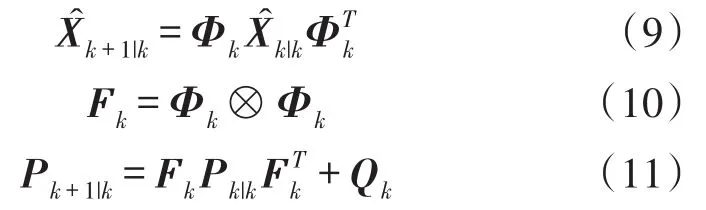
②量测更新：

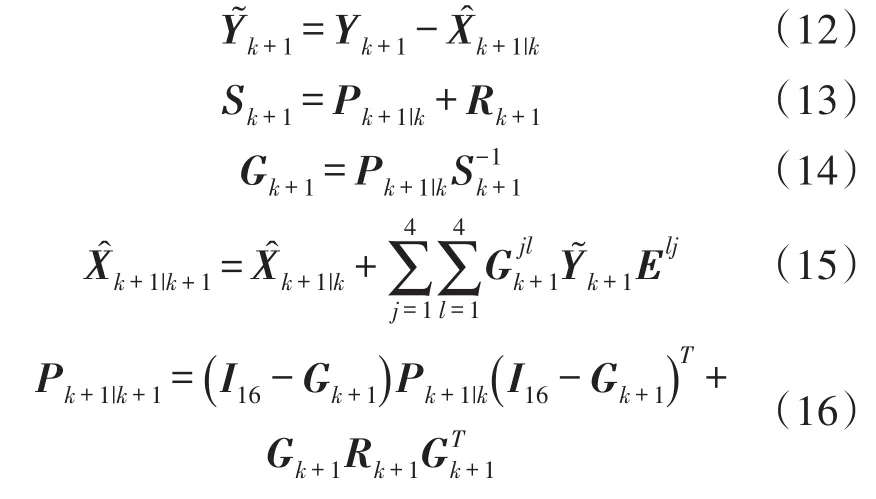
其中，

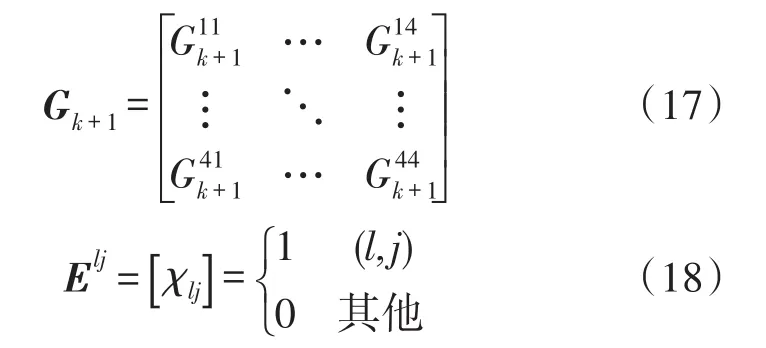
由式（9）～式（18）可知，矩阵Kalman滤波是一种线性Kalman滤波，满足线性Kalman滤波的最小方差特性，且易于实际系统中应用。

2.2 自适应滤波

由于线性Kalman滤波需要准确已知的量测噪声矩阵Rk+1，才能实现最优滤波的效果，但在实际系统中，往往不能准确得到。当量测噪声统计不准确时，系统只能达到次优滤波的效果。因此，本节在线性矩阵Kalman滤波的基础上，引入残差匹配自适应滤波技术，通过估计的量测噪声，对滤波算法进行补偿，有效提高了在量测噪声矩阵未知的情况下，估计姿态的精度和稳定性。

残差匹配自适应是一种常用的自适应滤波方法，利用残差匹配自适应滤波能够有效的减小量测噪声未知情况下，矩阵Kalman滤波对姿态估计结果的影响。所以，本文利用K-矩阵归一化特性，结合残差匹配技术，对上述矩阵Kalman滤波算法进行改进。由K-矩阵的归一化特性可知：

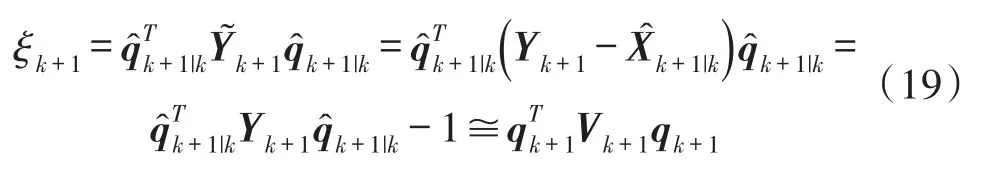
根据新息匹配原理，得到：

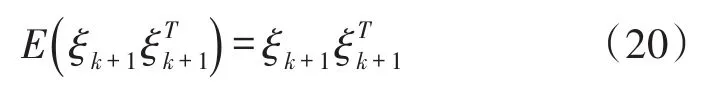
对式（20）进行求解可得：

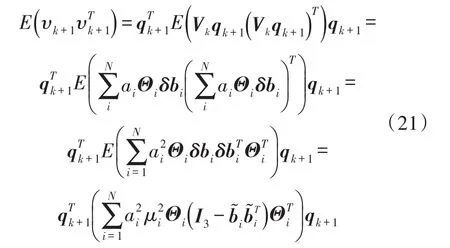
假设每次量测噪声都具有相同的误差类型，则式（21）可以简化为：

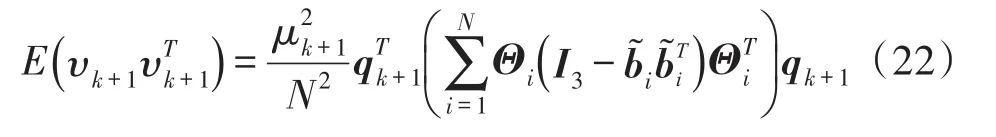
其中，

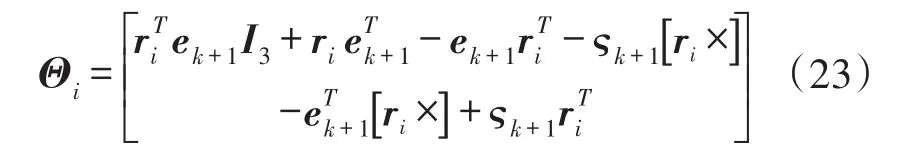
根据式（19）～（23）分析，利用四元数一步预测作为最优四元数代入式（22），结合式（19），则估计的量测噪声可表示为：

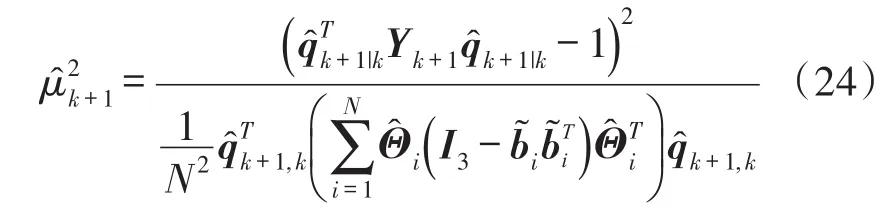
利用式（24）估计的量测噪声，代入矩阵Kalman滤波算法，计算量测噪声矩阵Rk+1，即可实现基于K-矩阵的自适应矩阵Kalman滤波。

3 最优四元数提取及误差计算

由于矩阵Kalman滤波估计的状态量为姿态K-矩阵，为直观表示姿态误差，需要从估计的最优K-矩阵中提取姿态角信息。利用K-矩阵定义及Wahba问题可知，姿态最优四元数为K-矩阵对应特征值为1的特征矢量。在求解最优姿态矩阵时，利用罗德里格斯参数法，得到最优姿态四元数为

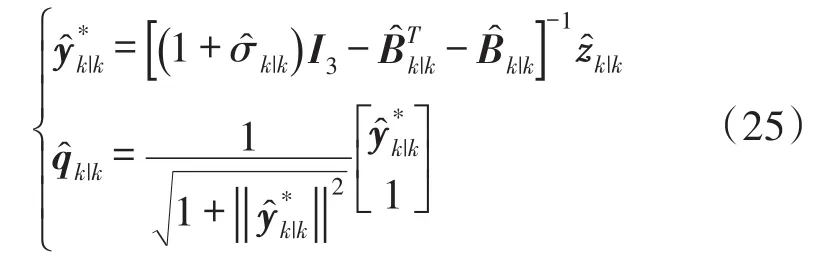
为分析方便，定义估计最优四元数与真实MEMS姿态四元数之间的误差四元数为：

其中，qk表示真实姿态四元数，δςk|k表示误差四元数标量部分，δϕk|k表示旋转误差角。

4 实验验证

本节设计仿真实验验证本文提出的自适应矩阵Kalman滤波算法。假设传感器零偏及安装误差均已通过校正获得，并补偿到系统中。仿真过程中，设定陀螺随机噪声为，真实量测噪声为μ=1°，考虑MEMS传感器以固定角速度绕z轴旋转，旋转角速度为ω=8π/7 200×[0 0 1]Trad/s。为仿真自适应滤波，假设不准确的量测噪声选取为μ=0.01°，仿真时间设定为5 400 s，系统开始采用线性矩阵Kalman滤波，在运行到2 000 s后采用自适应滤波。滤波初始参数设定为仿真结果如下图所示。

图1表示估计的误差四元数，从图1可以看出，误差四元数满足归一化特性，且在2 000 s之后，噪声特性明显减小。

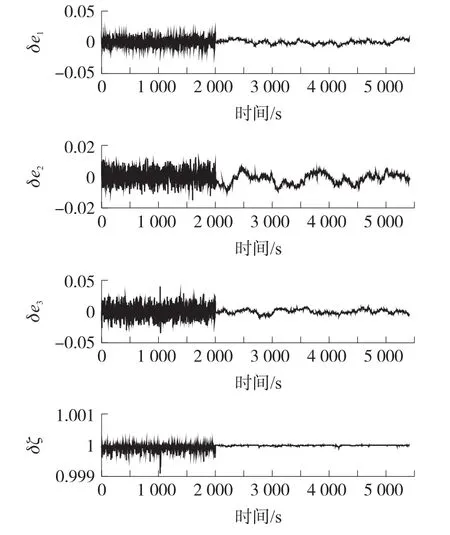
图1 误差四元数

图2表示量测噪声，其中蓝色实线表示滤波算法中实际使用的量测噪声，红色虚线表示真实的量测噪声。

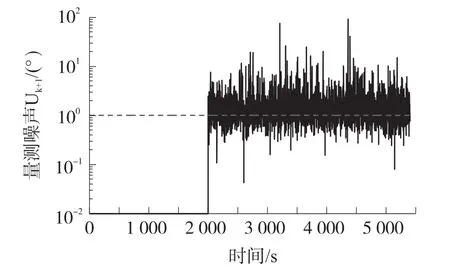
图2 估计量测噪声

从图2可以看出，自适应滤波能够估计量测噪声，并利用估计的量测噪声补偿未知的初始值。这有利于矩阵Kalman滤波提高姿态K-矩阵的估计精度。

图3表示旋转误差角，从图3可以看出，旋转误差角没有明显的发散现象，这是由于矩阵Kalman滤波的调节作用，利用磁强计及加速度计为参考基准，校准陀螺仪更新的姿态。由旋转误差角可知，在前2 000 s内系统旋转误差角均值为1.2 003°，标准差为0.641 5°，体现为姿态估计精度差，噪声特性明显，这是因为线性矩阵Kalman滤波直接采用预设的量测噪声进行姿态估计，由于预设值较小，滤波结果体现为对量测信息的可信度较高，因此滤波结果噪声较大。在2 000 s之后，采用自适应滤波估计量测噪声，旋转误差角均值稳定在0.601 9°左右，标准差为0.300 9°。统计结果表明自适应滤波具有更高的滤波精度及更好的滤波稳定性。

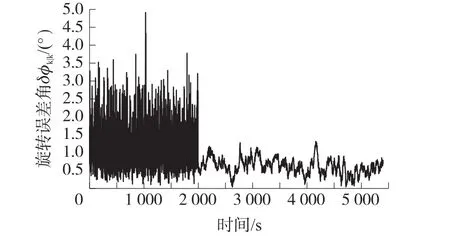
图3 旋转误差角

5 结论

本文研究了一种基于残差匹配的自适应矩阵Kalman滤波，并且针对MEMS应用，设计了仿真实验。算法实现过程中，利用K-矩阵的归一化特性，设计了一种特殊的残差计算方法。利用自适应矩阵Kalman滤波的迭代原理，对传感器量测噪声进行实时估计，并且利用估计的量测噪声对矩阵Kalman滤波进行校正。

针对MEMS实际系统应用，设计了仿真实验，仿真实验结果表明，本文提出的自适应滤波能够有效的估计未知的量测噪声，克服了线性矩阵Kalman滤波算法需要已知的量测噪声模型的缺点，并且提高系统姿态的估计精度和稳定性。此外，该滤波算法可以进行MEMS传感器初始对准，为MEMS惯性导航应用提供了新的有效方法。

［1］马建萍.GPS辅助捷联惯导系统动基座初始对准新方法［J］.传感技术学报，2010，23（11）：1656-1661.

［2］孙伟，李婉秋，初婧，等.基于误差修正技术的井下人员MEMS定位方法［J］.传感技术学报，2014，27（7）：898-904.

［3］赵鹤，王喆垚.基于UKF的MEMS传感器姿态测量系统［J］.传感技术学报，2011，24（5）：642-646.

［4］米刚，田增山，金悦，等.基于MIMU和磁力计的姿态更新算法研究［J］.传感技术学报，2015，28（1）：43-48.

［5］苏菲，金志刚，王柄鉴.基于惯性传感器的便携式消防员搜救系统［J］.计算机应用研究，2015，32（12）：3677-3681.

［6］Wachter Z.A Cost Effective Motion Platform for Performance Testing of MEMS-Based Attitude and Heading Reference Systems［J］.Journal of Intelligent&Robotic Systems，2013，70（1-4）：411-419.

［7］Madgwick S O H，Harrison A J L，Vaidyanathan R.Estimation of IMU and MARG Orientation Using a Gradient Descent Algorithm［C］//Rehabilitation Robotics（ICORR），2011 IEEE International Conference on.IEEE，2011：1-7.

［8］孙伟，丁伟，李瑞豹，等.基于小波降噪的MEMS惯导系统对准方法研究［J］.传感技术学报，2015，28（6）：814-818.

［9］高勇，曹娟娟，唐海红，等.磁强计辅助基于MEMS惯性器件SINS的初始对准方法研究［J］.航天控制，2013，31（3）：50-54.

［10］Markley F L，Crassidis J L.Fundamentals of Spacecraft Attitude Determination and Control［M］.Springer，2014.

［11］Shuster M D，Oh S D.Three-Axis Attitude Determination from Vector Observations［J］.Journal of Guidance，Control，and Dynamics，1981，4（1）：70-77.

［12］Markley F L，Crassidis J L，Cheng Y.Nonlinear Attitude Filtering Methods［C］//AIAA Guidance，Navigation，and Control Conference.2005：15-18.

［13］Choukroun D，Weiss H，Bar-Itzhack I Y，et al.Kalman Filtering for Matrix Estimation［J］.Aerospace and Electronic Systems，IEEE Transactions on，2006，42（1）：147-159.

［14］Choukroun D，Weiss H，Bar-Itzhack I Y，et al.Quaternion Estimation from Vector Observations Using a Matrix Kalman Filter［J］.IEEE Transactions on Aerospace and Electronic Systems，2012，48（4）：3133-3158.

［15］Choukroun D.Adaptive Optimal-REQUEST Algorithm for Attitude Determination［C］//AIAA Guidance，Navigation and Control Conference and Exhibit.2007：20-23.

［16］Choukroun D，Bar-Itzhack I Y，Oshman Y.Novel Quaternion Kalman Filter［J］.IEEE Transactions on Aerospace and Electronic Systems，2006，42（1）：174-190.

李 鑫（1983-），男（汉族），安徽省蒙城县人，硕士生，实验师，主要研究领域为MEMS技术及智能控制，lixin_cx@ 163.com。

Research on the Attitude Determination of MEMS Based on Adaptive Filter

LI Xin*，MENG Xiangfei，DAI Mei，GU Qimin
（School of Electric and Automatic Engineering，Changshu Institute of Technology，Changshu Jiangsu215500，China）

In view of the demand for attitude measurement system in the consumer electronics devices，a novel attitude determination method based on MEMS accelerometer，MEMS gyroscope and MEMS magnetometer is put forward in this paper.Because the statistics information of the measurement noise of the inertial sensors in the actual system is unknown，a matrix Kalman filtering for attitude determination algorithm based on the vector observer is introduced.In addition，the adaptive filtering method is designed on the basis of the residual matching technology.With this method，the measurement noise can be estimated，and the difficulty of obtaining the accurate statistics of measurement noise for the traditional matrix Kalman filtering is overcome.Finally，the simulation test is designed，and the results show that the rotation error angle is 0.609 1°，and the standard deviation is 0.300 9°，which indicates that the measurement noise of the sensors can be determinated effectively，and the adaptive filter is more accurate and more stable by comparing with the traditional matrix Kalman filtering.

MEMS；attitude determination；adaptive filter；matrix Kalman filter；observation vector

TP 212.9；V249

A

1004-1699（2016）12-1853-05

��7230

10.3969/j.issn.1004-1699.2016.12.012

2016-05-30修改日期：2016-07-15