中美两国混凝土规范中板挠度变形力学模型的计算对比
2017-01-12刘玉林
刘玉林
(中国核电工程有限公司, 北京 100840)
中美两国混凝土规范中板挠度变形力学模型的计算对比
刘玉林
(中国核电工程有限公司, 北京 100840)
在实际工程中应用中,钢筋混凝土板是使用非常广泛的结构件之一,混凝土板的设计是土木工程结构设计的基础,但目前混凝土板的挠度没有专门的计算公式,通常是通过借用由梁推导出板的挠度公式。同时不同国家对工程领域所遵循的设计规则存在一定的差异,本文针对中美两国在建设领域在挠度计算方面设计规则的差异,对我国《混凝土结构设计规范》(GB50010-2010)和美国ACI318M-08相关挠度的计算规范进行了对比分析,并设置了3组试验。结果表明,中国规范和美国规范均未能较好对混凝土板的挠度变化进行描述。采用这两个规范计算挠度,会对板结构的使用性和可靠度造成影响,中美的规范均未对板弯曲的双向性进行深入考虑;在计算混凝土板挠度时,因梁受力比较复杂,套用梁的公式计算挠度会产生较大误差。
混凝土; 规范; 挠度; 力学模型
0 引言
中国和美国国情不同,因而在建设工程领域的设计规则存在一定的差异,这给两国设计人员交流造成了障碍。为促进交流和加强两国在工程设计领域的进一步合作,在两国之间进行使工程建设的经验共享,需要对两国建设工程规范进行比较[1-3]。通过对比规范,为结构设计其他方面的规定提供参考[4-7]。
在实际工程中应用中,钢筋混凝土板是使用非常广泛的结构件之一,按照混凝土板的结构特点,板分为小挠度板和大挠度板[8]。在横向荷载作用下,小挠度板发生弯曲变形,并以弯曲变形抵抗外加的横向荷载。混凝土板在各类用途的建筑中具有非常广泛的应用[9-12],土木工程在结构设计以混凝土板为基础。在钢筋混凝土板的设计中,板构件正常使用极限状态设计重要内容之一就是挠度计算,这在各类建筑工程、桥梁工程等是经常要用到的,在实际应用中,由于没有专门的挠度计算公式,大部分板的挠度计算公式是参考梁的计算公式,但梁尺寸和配筋率等都比板要大,受力也比板要复杂,套用梁的公式计算挠度会产生较大误差[13]。
在实际结构设计中,通过对板挠度准确控制,可合理选定板的厚度,从而降低了成本[14]。本文主要在板设计与计算方面,对我国《混凝土结构设计规范》(GB50010-2010)、美国混凝土结构规范要求《Building Code Requirements for Structural Concrete》(ACI318M-08)的差别进行对比[15],对两国规范应用于混凝土板挠度计算时的精度进行了讨论。
1 两国材料强度转换
1.1 混凝土的强度转换
我国的GB50010-2010规范中,采用立方体抗压强度标准值进行混凝土强度的划分,共划分为14个等级,实际工程设计中常用的有C15,C20,C25,C30,C35,C40等,最高等级的混凝土强度为C80。美国的ACI318M-08规范中,采用圆柱体抗压强度进行混凝土强度的划分,共有C24.5、C32、C40、C49共4个等级,其中混凝土的强度最高等级为C49。表1以我国的GB50010-2010规定的混凝土强度为基准,给出美国规范对应的强度指标转换关系。

表1 中美规范对应的混凝土强度指标转换关系Table1 Therelationshipbetweenchineseandamericanconcretestrengthindex中美规范强度符号C15C20C25C30C35C40中国GB50010-20107296119143167191美国ACI318-08——117140163186
1.2 钢筋的强度
在中美两国的规范中,美国钢筋屈服强度fy和中国规范fyk是相同的,中美对钢筋强度规范的不同之处在于中国采用的计算依据是抗拉强度设计值,而美国采用计算依据是抗拉强度标准值。两国常用的钢筋强度主要有3种,级别分别为C40,C60和C75,屈服强度分别为280、420、 520 MPa。
2 混凝土板带弯曲变形
混凝土板带的跨度为板的短跨Lx,在板带上,表面作用有方向向下的均布荷载q(x);在两侧面上,有相邻板带所施加的方向向上的剪力q′(x)、扭矩Myx及弯矩My产生的水平方向的拉、压应力,这导致截面抗弯刚度变小,而增加整体的弯曲变形,同时减小了截面抗剪刚度,如图1所示。
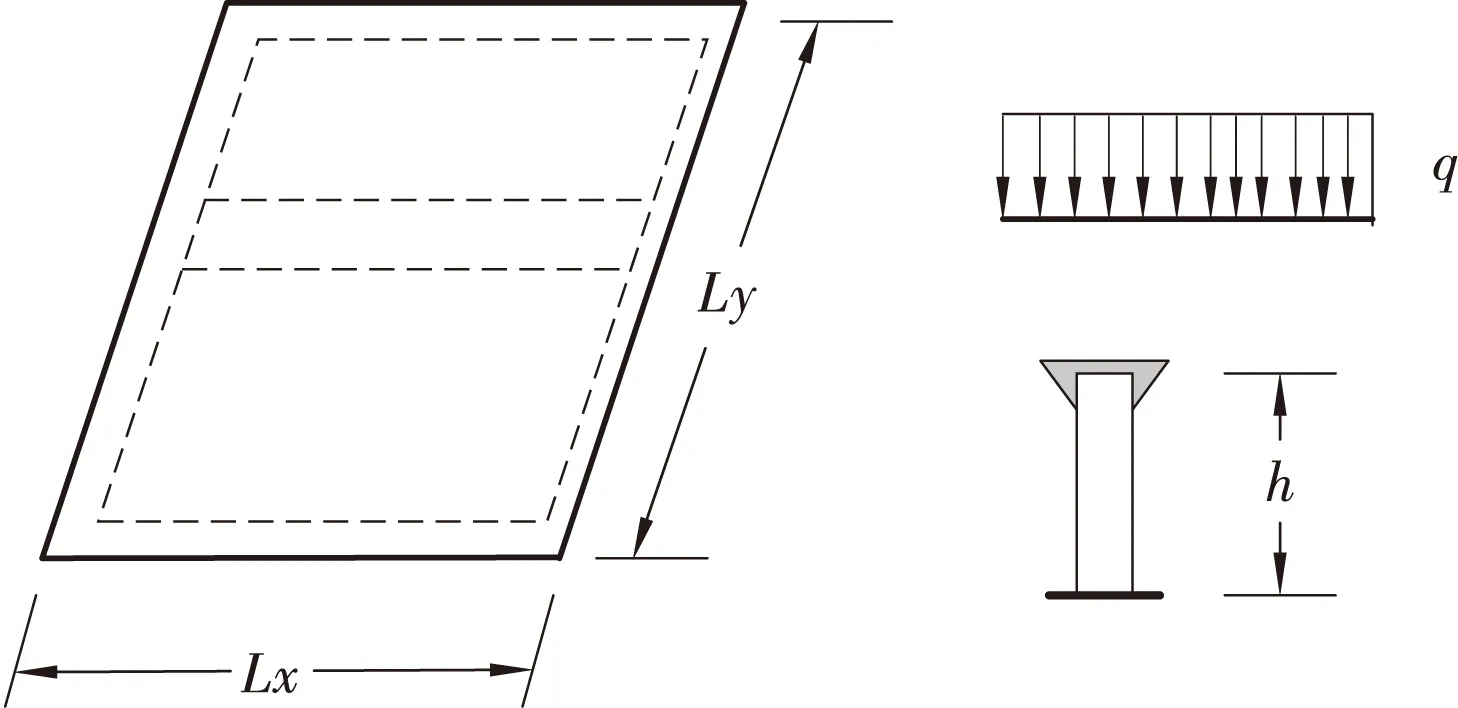
图1 板带及其受力示意图Figure 1 The schematic diagram of the plate and its force
3 两国的计算体系
3.1 中国的《混凝土结构设计规范》
中国目前执行的《混凝土结构设计规范》(GBS0010-2010)中给出,在对钢筋混凝土受弯构件进行短期刚度计算时,通常采用实际经验与理论相结合的公式,见公式(1)。
(1)

(2)
公式(2)中:fsk表示混凝土轴心抗拉强度的标准值;σsk表示纵向受拉钢筋应力,σsk的计算见式(3)。
(3)
公式(3)中:Mk表示荷载效应的弯矩;ρsc表示受拉钢筋的配筋率。
3.2 美国的《房屋建筑混凝土结构规范》
在美国《Building Code Requirements for Structural Concrete》(ACI318M-08)中,对于混凝土构件短期刚度的计算,规范对构件的有效惯性矩进行计算通常采用公式(4)。
(4)

(5)

4 试验与模型计算
4.1 试验试件
为更好的对中美两国规范的混凝土板挠度计算公式进行比较,对两国公式的精度进行研究,本文设计了3组试件,制作混凝土板共15块,其长与宽的比值均为7∶4,其中每组各5个试件,试件尺寸见表2,混凝土强度等级C25,钢筋为HPB335,其中HB1、HB6、 HB11板试件尺寸及主要钢筋配置如图2所示,受力钢筋 φ8@150,分布钢筋φ8@ 150。

表2 试件尺寸Table2 Thedimensionsoftestspecimens分组编号尺寸(mm×mm)板厚/mm第1组HB12625×150095HB23500×200095HB34375×250095HB45250×300095HB56125×350095第2组HB62625×150095HB73500×200095HB84375×250095HB95250×300095HB106125×350095第3组HB112625×150095HB123500×200095HB134375×250095HB145250×300095HB156125×350095

图2 板试件的顶面尺寸Figure 2 The size of the slab
4.2 试件板设计
本文中,试件设计为单向的混凝土板,板的一对边为简支设计,另外两边为自由设计,试验跨度为2.5 m。荷载是均布荷载,对板面进行网格划分,模拟均布荷载采用的构件是铸铁块,其中图3表示放置加载铸铁砝码的网格,图4表示试件支座和加载示意图,荷载分别取3.0,7.0,9.0 kN/m2。

图3 实验放置砝码的网格Figure 3 The placement of weights grid

图4 实验试件支座示意图Figure 4 The schematic of test piece
4.3 数据采集
在本试验中,对跨中挠度值的采集是主要目的,由于挠度与板曲率直接关联,因而一并对挠度值和相应部位的应变值都进行采集,这样有利于检测出相关问题,从确保试验质量。实验中,虽然每个试件的尺寸大小不同,但其长与宽的比例均为7∶4,试件在4.5 kN/m时出现裂缝。裂缝在加载初期还未出现之前,混凝土板的挠度增长比较慢,跨中的挠度小于2.5 mm,挠度与荷载变化表现出线性增大的趋势,这说明,钢筋混凝土单向板在开裂之前符合弹性假定。裂缝在加载的中期开始出现之后,混凝土板的挠度这是增加较快,挠度与荷载变化表现出的是非线性关系,混凝土板试件刚度在这个阶段是减弱的。当板的挠度值达到正常使用的的极限时,立即停止加载。对于试件板跨中各点的挠度,本文的测定采用是百分表,实验测试结果表明,试件板跨中心点的位置挠度值较小,跨中两侧的挠度较大,这符合理论分析,对于单向板来说,可认为跨中各点具有相同的挠度。
4.3.1 板跨中顶面布置
在混凝土板跨中顶面,安装有12个应变片,纵向粘贴的应变片共6个,横向粘贴的应变片也是6个,如图5所示。

图5 板跨中顶面布置图Figure 5 The layout drawing of plate span
4.3.2 板跨中底面布置
在混凝土板跨中底面,安装有6个应变片,均为横向粘贴,如图6所示。在混凝土板底面,同时在相应位置安装百分表6个,主要是为了测量对6个应变片点的挠度,同时在0.25处,安装6个对比百分表,如图7所示。

图6 板跨中底面布置图
Figure 6 The layout drawingof plate span

图7 挠度测量点的布置图Figure 7 The arrangement of deflection measurement points
4.4 两国规范计算分析
采用中国和美国规范的挠度计算公式,获得板跨中的挠度值,然后将计算值与试验值做柱状图进行比较,分析两国规范的计算方法的精度。其中图8是在荷载为3.0 kN/m2,时的挠度对比图;图9是在荷载为7.0 kN/m2时的挠度对比图;图10是在荷载为9.0 kN/m2时的挠度对比图。
4.4.1 3.0 kN/m2时的挠度对比
从图8可以看出:荷载小于开裂荷载的情况下,即3.0 kN/m2<4.5 kN/m2,对于我国GB 50010-2010规范的公式,计算的挠度值要大于试验值,这说明我国规范较高的预估了挠度值;美国ACI318-08规范的的公式,计算的挠度值与试验值相差较小,吻合比较较好,但比试验值略小,对挠度值的预估较低。

图8 荷载3.0 kN/m2时挠度图Figure 8 Deflection comparison chart when the load is 3.0 kN/m2
4.4.2 7.0 kN/m2时的挠度对比
由图9可知:在荷载大于开裂荷载的情况下,即7.0 kN/m2>4.5 kN/m2,我国规范的挠度计算值与试验值比较接近,对挠度值的预估较准确;美国规范的挠度计算值与试验值相比变的要小,约为实验值的50%,对挠度值的预估较低。
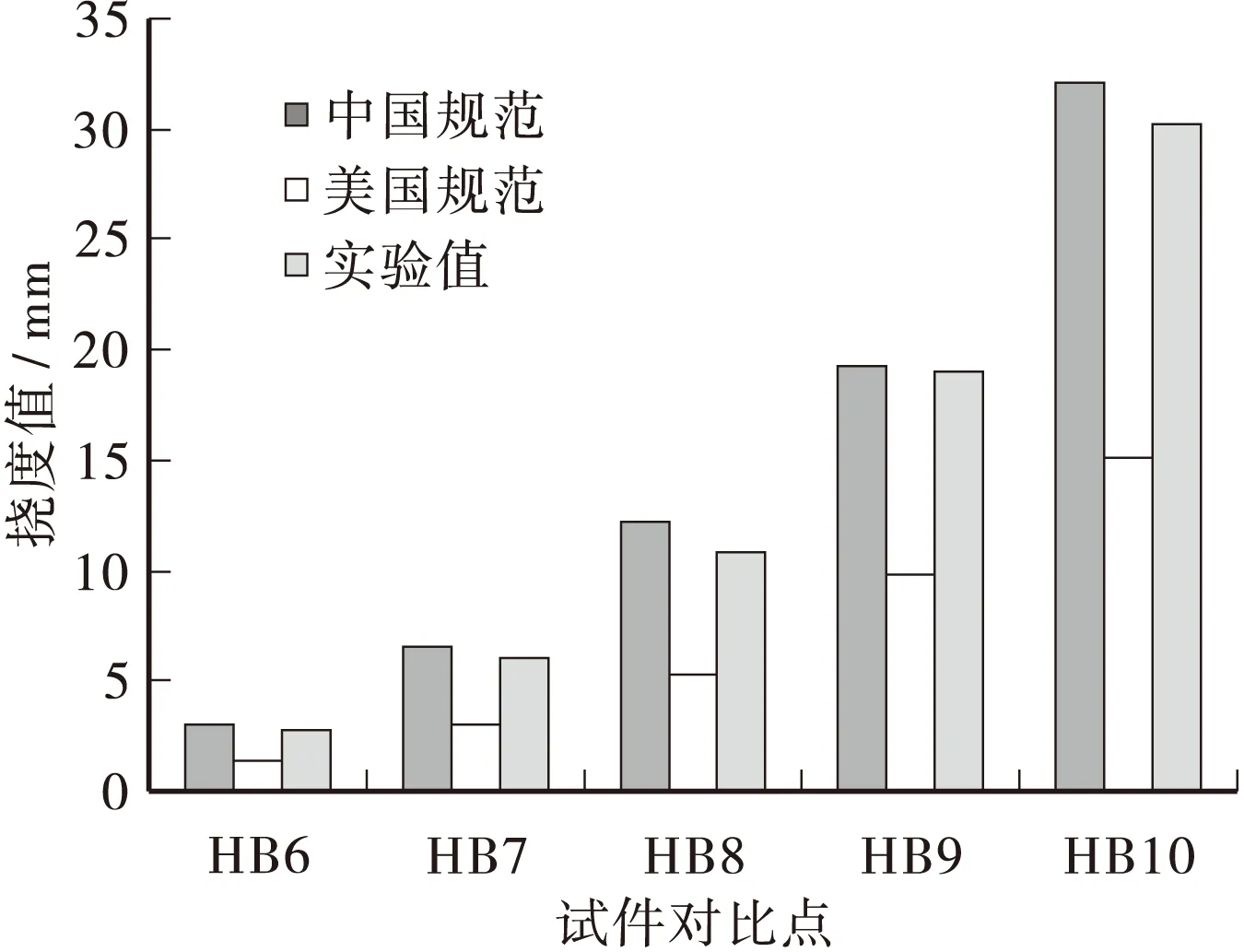
图9 荷载为7.0 kN/m2时挠度图Figure 9 Deflection comparison chart when the load is 7.0 kN/m2
4.4.3 9.0 kN/m2时的挠度对比
从图10可以看出:荷载大于开裂荷载的情况下,即9.0 kN/m2>4.5 kN/m2,我国GB 50010-2010规范的挠度计算值要小于试验值,这说明我国规范较低预估了挠度值;美国ACI318-08规范的挠度计算值要比试验值小很多,约为实验值的70%,对挠度值的预估较低。同时美国规范的挠度计算值还小于我国规范的挠度计算值。
同时对比图8、图9和图10,发现混凝土单向受弯时挠度的开展和板的长短边比有关。在其它条件不变时,单向受弯时的挠度比值随着长短边比值的

图10 荷载为9.0 kN/m2时挠度图Figure 10 Deflection comparison chart when the load is 9.0 kN/m2
增加而增大。另外,在弹性阶段和塑性阶段,中国规范和美国规范均未能较好对混凝土板的挠度变化进行描述。在较小的荷载下,我国GB 50010-2010规范可作为挠度计算的依据,在较大荷载下,采用我国规范计算结果要偏小,需要进行修正。这主要是由于混凝土材料本身所具有弹性和塑性等有一定的关系,同时与混凝土板自己弯曲特殊性也有一定的关系。
5 结论
① 中国规范和美国规范均未能较好对混凝土板的挠度变化进行描述。采用这两个规范计算挠度,会对板结构的使用性和可靠度造成影响,中美的规范均未对板弯曲的双向性进行深入考虑;在计算混凝土板挠度时,因梁受力比较复杂,套用梁的公式计算挠度会产生较大误差。
② 在较小的荷载下,我国GB 50010-2010规范可作为挠度计算的依据,在较大荷载下,采用我国规范计算结果要偏小,需要进行修正。无论荷载多大时,美国规范的挠度计算值均小于我国规范的挠度计算值。为了今后在实际应用中能更精确的计算混凝土的挠度值,需要中美两国不断加强理论和试验的研究工作。
[1] 张维,张元琦,孟桂萍.中美规范钢筋混凝土大偏压柱配筋比较[J].石油化工设计,2014,31(1):10-13.
[2] 万超.中美规范关于混凝土框架柱挠曲二阶效应的对比分析[J].建筑与结构设计,2014(8):37-41.
[3] 单建华,聂晶,卢佳.中美规范素混凝土构件设计比较[J].低碳世界,2016(2):69-71.
[4] 张红霞,刘海峰.中美规范钢筋混凝土纯扭构件承载力分析对比[J].四川建筑科学研究,2014,40(5):168-179.
[5] 杨京华,张明华.PKPM、盈建科、理正钢筋混凝土双向板挠度计算讨论[J].建筑设计管理,2014(11):72-76.
[6] 李明鸿,万水,蒋正文,等.波形钢腹板混凝土组合梁挠度计算的初参数法[J].华南理工大学学报:自然科学版,2015,43(2):66-75.
[7] 童根树,陈迪.腹板开孔的钢-混凝土组合梁的挠度计算[J].工程力学,2015,32(12):168-179.
[8] 王新泽.钢管混凝土拱桥环境温度引起的应力挠度分析[J].铁道建筑,2016(2):39-43.
[9] 车轶,孙阔.混凝土深梁抗剪强度中美规范设计对比[J].低温建筑技术,2014(9):71-74.
[10] 王俊,孔亚美,刘立新.折线先张法预应力混凝土梁长期挠度实用计算公式[J].郑州大学学报:工学版,2015,36(2):47-52.
[11] 付攀,樊海渊,牟金磊.水下爆炸作用下加筋板变形挠度计算方法[J].江苏船舶,2014,31(3):10-11.
[12] 赵宝生,王纪伟,郑勇,等.使用状态下钢筋混凝土双向板的挠度研究[J].工程质量,2015,33(12):19-23.
[13] 王俊,王博,孔亚美.预应力混凝土梁徐变挠度影响因素分析与计算模式构建[J].建筑结构,2016,46(6):95-100.
[14] 于峰,黎德光,徐国士,等.偏压PVC—FRP管钢筋混凝土柱荷载-挠度关系数值分析[J].玻璃钢/复合材料,2015(8):18-25.
[15] 李朋,郑鸿飞,张宪堂,等.基于中美规范的高强钢筋混凝土梁受剪承载力对比分析[J].山东科技大学学报:自然科学版,2016,35(1):66-73.
Calculation and Comparison of the Deformation Mechanics Model of Slab Deflection in Concrete Norms of China and America
LIU Yulin
(China Nuclear Power Engineering Co., Ltd, Beijing 100840, China)
The reinforced concrete slab is used very extensive in practical engineering applications,the structural pieces of concrete slab design is the basis of civil engineering structure design,but the deflection of concrete slab of no special formula,usually by borrowing from the beam push the deflection formula is derived in the.And different countries in the field of engineering should follow the design rules exist certain differences.the differences of Sino-US two countries in the field of construction in the deflection calculation design rules for,on China's "code for design of concrete structures"(GB50010-2010)and deflection of the American ACI318M-08 computing specification of the comparative analysis,and set up the test 3 group.The results show that Sino-US deflection calculation specification have failed to accurately reflect the plate deflection and deflection calculation results will impact on the plate structure of the usability and reliability,Sino-US specification were not on plate bending of the two-way were in-depth consideration;in the calculation of concrete slab deflection,beam is more complex,apply formula of the beam deflection calculation will produce large errors.
concrete; standard; deflection; mechanical model
2016 — 08 — 18
刘玉林(1981 — ),男,河北安国人,高级工程师,硕士,主要研究方向:结构设计。
TU 435
A
1674 — 0610(2016)06 — 0078 — 04
