基于可靠度的柔性系杆更换研究

唐 辉, 崔秀鹏, 高燕梅, 周志祥，4

(1.中交路桥技术有限公司， 北京 100011; 2.北京中交华联科技发展有限公司， 北京 100101; 3.重庆交通大学 土木建筑学院， 重庆 400074; 4.山区桥梁与隧道工程国家重点实验室培育基地， 重庆 400074)

基于可靠度的柔性系杆更换研究

唐 辉1, 崔秀鹏2, 高燕梅3, 周志祥3，4

(1.中交路桥技术有限公司， 北京 100011; 2.北京中交华联科技发展有限公司， 北京 100101; 3.重庆交通大学 土木建筑学院， 重庆 400074; 4.山区桥梁与隧道工程国家重点实验室培育基地， 重庆 400074)

柔性系杆作为系杆拱桥的关键构造，其索力损失必然对桥梁的可靠性能造成重要影响，索力损失到一定程度需及时进行更换。依托某跨径跨布置为46 m+202 m+46 m柔性系杆飞燕式钢管混凝土拱桥，以系杆索力损失10%为初始状态，提出4种系杆更换方案(单侧同时更换1根、2根、3根、4根，上下游侧同时进行更换)，采用一次二阶矩(JC)法及PNET法，分析了不同方案下桥梁构件及体系的可靠度变化规律。结果表明： 方案1、2均可行，方案1安全但施工步骤多，方案2能够保证桥梁的最低安全等级，同时尽可能缩短施工时间，建议采用方案2。

柔性系杆； 更换方案； 可靠度

0 引言

柔性系杆是柔性系杆拱桥的关键构件，被称为系杆拱桥的“生命索”，但是由于其自身受力和结构的复杂性，导致其非常容易损坏。在桥梁的使用期间，系杆会由于诸多病害导致其索力不断损失，索力损失到一定程度，若维修或更换不及时，就可能发生系杆断裂，影响桥梁的正常使用甚至造成危险[1]。

系杆拱桥由于其美观性，大多修建在城市附近，客货车运营非常繁忙，客、货车调车频度极高。因此，进行桥梁系杆更换时，宜不中断交通，在关键工序、关键部位的施工过程中，为保证桥梁结构和施工安全以及测试工作顺利进行，必要的交通中断是不可避免的，但需尽量减少现场作业，将对交通的影响将至最低[2-4]。

目前对系杆损坏后的更换大部分都是根据经验切一根换一根，没有系统的研究过，本文以系杆拱桥可靠度理论及有限元分析理论为基础，针对依托工程提出了4种系杆更换方案，采用一次二阶矩(JC)法及PNET法，分析了不同方案下桥梁构件及体系的可靠度变化规律。旨在于找到一种系统、简洁、安全、高效的系杆更换的方法。

1 系杆拱桥可靠度分析方法

1.1 结构上作用的概率模型及作用随时间的变化

① 恒荷载。恒荷载作用属于永久作用，采用正态分布的随机概率模型[5](见表1)。

表1 恒载重量的随机概率模型Table1 Randomprobabilitymodelofcomponentweight荷载种类分布类型平均值/标准值κG或κτ变异系数δG或δτ恒载正态1014800431

② 汽车荷载。汽车作用效应分为一般运行状态和密集运行状态，采用正态分布随机概率模型[5](见表2)。

表2 汽车荷载的随机概率模型Table2 Randomprobabilitymodelofvehicleload随机情况汽车运行状态效应种类分布类型平均值/标准值κSQ变异系数δSQ实际基准期最大值分布一般运行状态密集运行状态弯矩剪力弯矩剪力正态正态0668401994059250200807882010820709600964

可变荷载效应在使用寿命期内是发生变化的，若在设计基准期T0内可变荷载效应的平均值和标准差分别为气μQ T0和σQ T0，则在剩余使用寿命期T内可变荷载效应的平均值μQ T和标准差σQ T可以表示为:

μQ T=μQ T 0+ln(T/T0)/α

(1)

σQ T=σQ T0

(2)

式中：

(3)

根据桥梁实际的运行情况，考虑桥梁在90%的时间内处于一般运营状态，而10%的时间内处于密集运营状态[6]。则有:

μQ=90%×μQ1+10%×μQ2

(4)

(5)

③ 人群荷载人群荷载采用采用Ⅰ型分布[5](见表3)。

表3 人群荷载的随机概率模型Table3 Randomprobabilitymodelofcrowdload标准值Lki/(kN·m-2)分布类型平均值/标准值κL变异系数δL30Ⅰ型0684702146

1.2 结构抗力统计模型及抗力随时间的变化

构件抗力一般可假定其服从对数正态分布[5](见表4)。

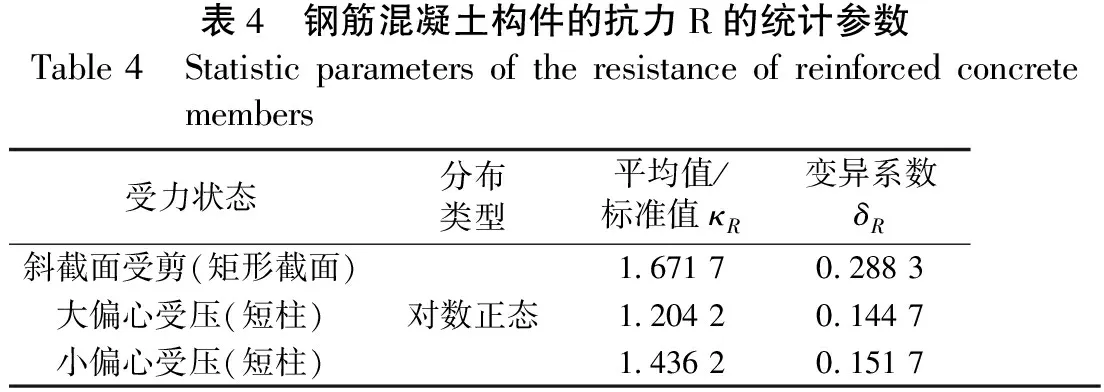
表4 钢筋混凝土构件的抗力R的统计参数Table4 Statisticparametersoftheresistanceofreinforcedconcretemembers受力状态分布类型平均值/标准值κR变异系数δR斜截面受剪(矩形截面)1671702883大偏心受压(短柱)对数正态1204201447小偏心受压(短柱)1436201517

规范中仅给出了钢筋混凝土构件的抗力统计参数，而钢管混凝土系杆拱桥中主要受力构件为主拱肋，属于小偏心受压构件，因此主拱肋的抗力统计参数参照钢筋混凝土构件的抗力参数计取。桥墩受力抗力采用偏心受压构件的抗力统计参数；受剪抗力参照矩形截面的抗力统计参数计取。

构件抗力随时间的变化通过将初始抗力乘以抗力衰减系数[6]，即：

R(t)=R0φ(t)

(6)

μR(t)=μR0φ(t)

(7)

δR(t)=δR0

(8)

式中:φ为结构抗力的衰减规律。

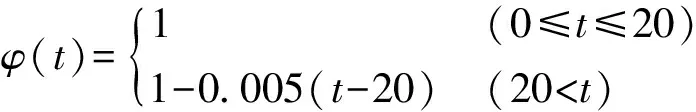
(9)

1.3 构件可靠度分析方法：一次二阶矩法(JC法)

系杆拱桥极限状态方程可表示为：

Z=g(R,S)=R-SG-SQ-SP

(10)

(11)

(12)

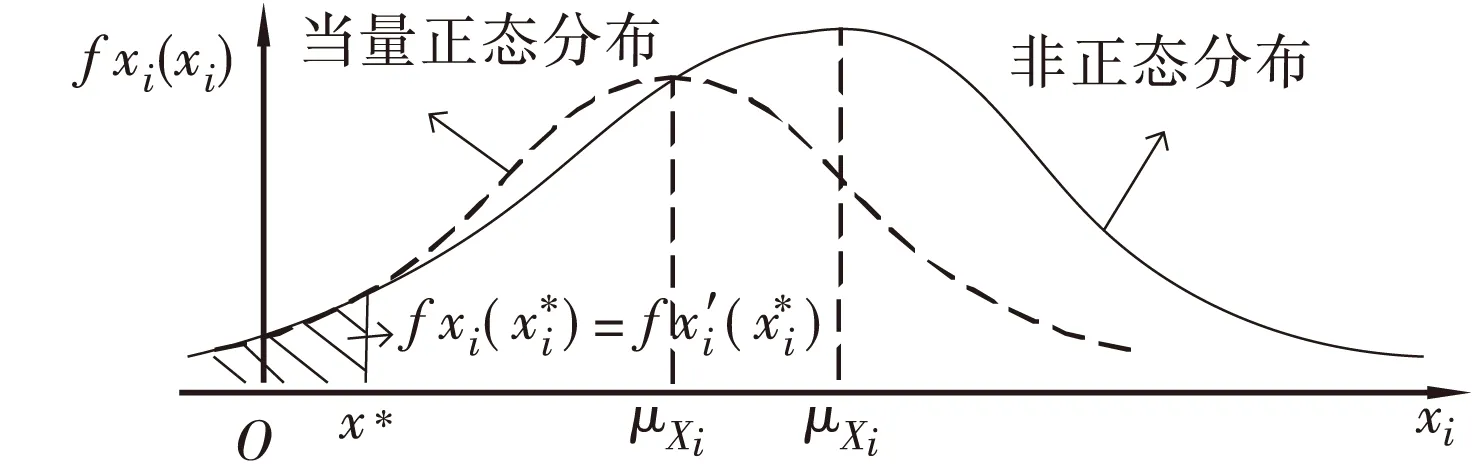
图1 JC法的当量正态化条件Figure 1 Equivalent normalization condition of the JC method

1.4 系杆拱桥体系可靠度分析方法：PNET法

系杆拱桥体系可靠度分析方法采用概率网络估算技术(Probabilistic Network EvaluationTechnique，简称PNET法)[7]。其基本原理：首先，根据彼此相关程度对主要的失效模式进行分组，每组选择其中主要失效模式作为代表的失效模式，然后假设典型的失效模式是相互独立的，然后根据下面的公式计算结构体系的可靠度：

(13)

则失效概率为

(14)

式中：m为所分组数。

各失效模式之间的相关关系采用下式计算[11]：

(15)

式中：αi,αj分别表示在i或j种失效模式下的单位向量。

构件可靠度计算及失效模式之间的相关系数通过Matlab编程实现。

针对系杆拱桥，在分析时可选择关键构件的控制截面作为研究对象：主拱肋选择拱脚、拱梁结合处、1/4L主拱、拱顶三个截面；系杆；主墩墩顶和墩底截面；边拱拱脚截面。

考虑以下几种极限状态：

① 主拱肋在最不利荷载作用下，抗弯和和抗压不超过极限强度；

② 桥墩在最不利荷载作用下，压应力不超过屈服强度，剪力不超过极限强度；

③ 边拱在最不利荷载作用下，压应力不超过屈服强度。

结构体系可靠度指标计算流程如图2所示。

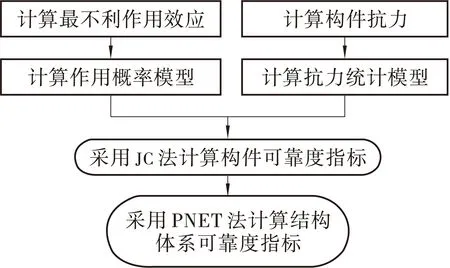
图2 结构体系可靠度指标计算流程Figure 2 The calculation process of the system reliability

2 系杆张拉与切割模拟方法及新系杆张拉力确定方法

2.1 系杆张拉与切割模拟

系杆张拉采用降温法模拟[13]。即将荷载大小换算为温度荷载加载到相应系杆上进行分析计算。在其他施工过程中，系杆的内力会随着外荷载的不同而发生变化，能真实地反应系杆内力变化情况。

系杆的切除实际上是面积在不断减小，若假定在单根系杆中，每根钢绞线的受力是均匀的，因此将每根钢绞线均建立成独立的单元，然后钢绞线的切断通过钝化钢绞线单元实现。

2.2 新系杆索力计算方法

① 待更换系杆索力测定。

准确地测定现有系杆索力是了解桥梁工作状态和换索索力取值的基本依据。由于桥面铺装加厚、增设附属设施等，使桥梁自重增加，因此长期恒载作用下实际与设计的索力有很大差异，系杆索力也肯定有一定损失，精确迅速测定索力是系杆更换工作的重要环节。索力测试精度要求误差不大于1 kN。

② 新系杆张拉力计算。

每一根新系杆进行张拉时，都会使其他系杆的内力发生变化。如果采用多次张拉，则在最后还需对系杆拉力进行统一调整，比较麻烦；如果采用一次张拉到位，则系杆需要超张拉，超张拉的索力可通过影响矩阵求解[14]，具体如下：

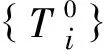
(16)

3 基于可靠度的柔性系杆更换研究

3.1 算例背景介绍

本文依托工程为某飞燕式钢管混凝土系杆拱桥，其跨布置为46 m+202 m+46 m。桥面宽26.2 m，设计荷载标准：汽-20,挂-100，该桥于1998年建成通车。主拱肋采用4-Φ750钢管混凝土构件。总体布置如图3所示。

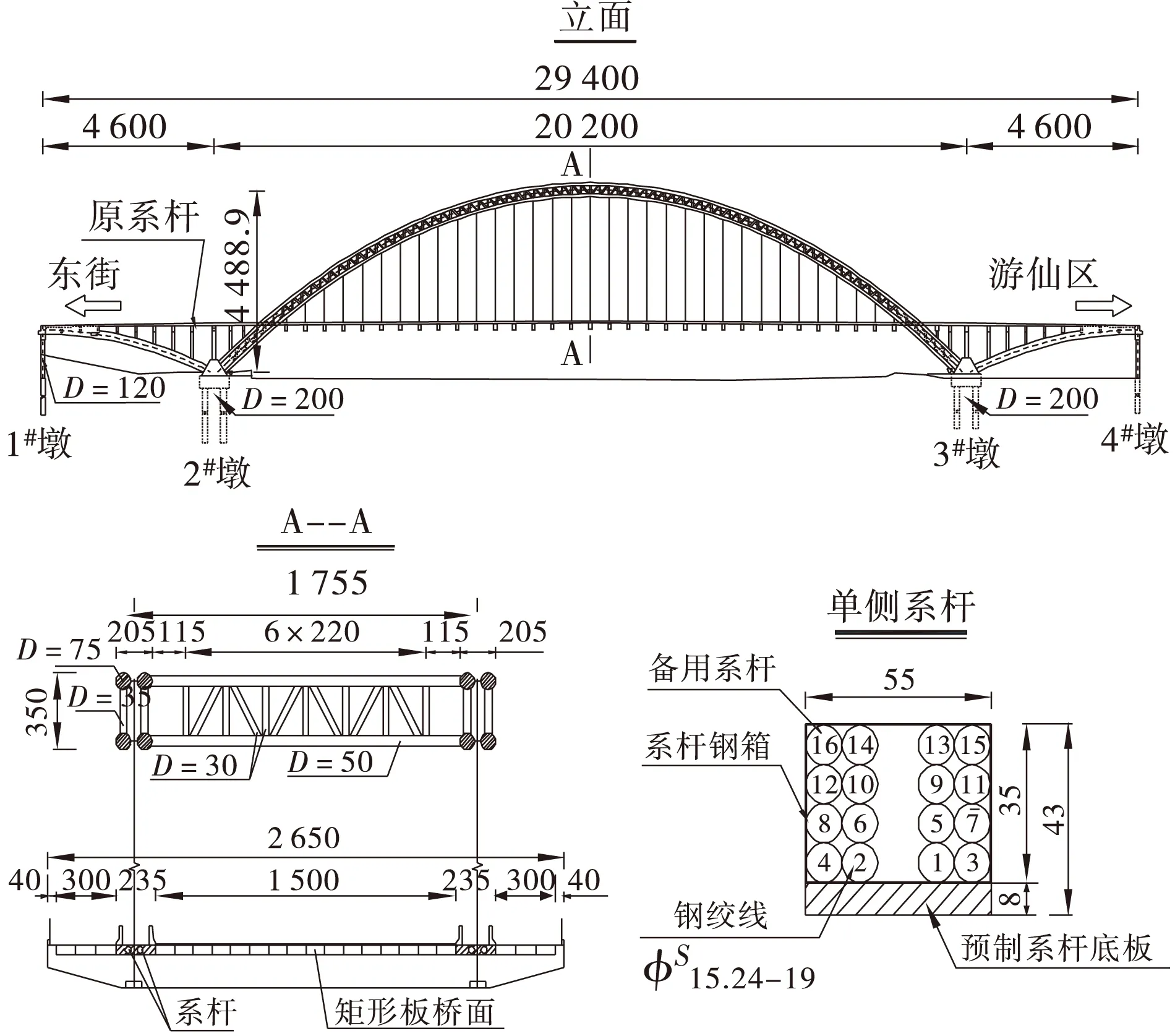
图3 某飞燕式钢管混凝土系杆拱桥总体布置图(单位： cm) Figure 3 Genaral layout of a concrete filled steel tube flexible tied arch bridge (unit: cm)

3.2 系杆更换方案设计

系杆构造如图3所示。根据每次更换系杆的根数以及临时系杆的设置方式，常规的系杆方式为一根一根的更换。这个常规的方式简单易行，但施工时间较长，对交通的影响较大，为克服传统方式的缺点，本文提出了新的系杆更换方式：即每次选择上下游两侧一个或多个同号系杆进行更换，上下游同号系杆同时进行更换，也可交替进行，其中以同时进行为最不利。每次系杆更换均以16#系杆为临时系杆，实施系杆更换时，禁止车辆及行人通行，每一个施工循环结束后，对车辆进行限重放行(见表5)，计算时参照89规范的车辆荷载执行，人群荷载不进行限制。分别考虑以下4种系杆更换方案(见图4)：

表5 4种方案模型计算荷载与限重标准Table5 Loadandweightlimitstandardsof4replacentschemes项目限重标准方案一整个车队最多允许1辆重车(总重30t，轴重13t)通行，20t以下的车不受限制方案二整个车队最多允许1辆重车(总重20t，轴重13t)通行，15t以下的车不受限制方案三整个车队最多允许1辆重车(总重15t，轴重10t)通行，10t以下的车不受限制方案四禁止车辆通行

3.3 最不利荷载效应计算

各控制截面最不利荷载效应通过Midas/Civil2012建立有限元模型进行计算，桥墩选择外侧最不利桥墩作为研究对象。各方案下以第一步最为不利，因此本文主要分析第一步时桥梁内力及可靠度变化。如图6所示。

系杆索力损失的对桥梁内力或应力的影响计入恒载里面，由于在不同工况内进行了限载，各构件最不利汽车荷载效应在不断发生变化。

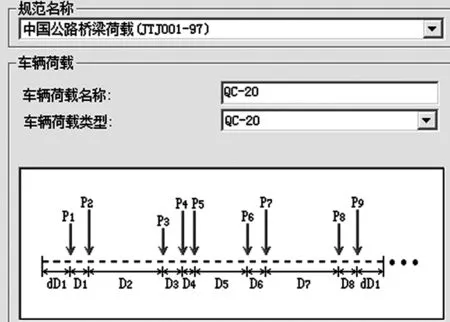
图5 方案1模型计算荷载Figure 5 Calculation load in scheme 1

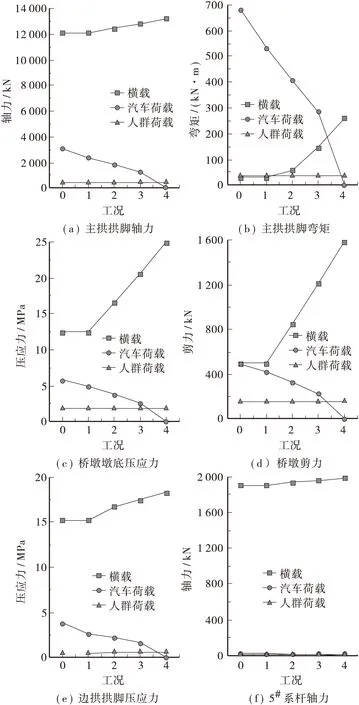
图6 不同工况下最不利荷载效应变化Figure 6 Unfavorable load effect under different replacement schemes

3.4 构件抗力计算

各构件抗力参照《钢管混凝土拱桥技术规程》(DBJ/T 13 — 136 — 2011)和《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)相关规定计算[15,16]。各截面抗力见表6。

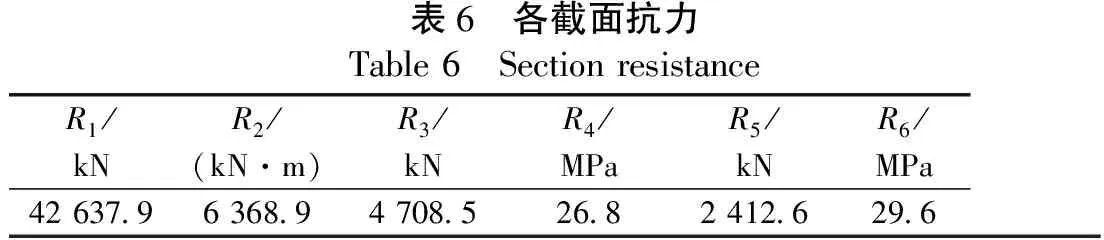
表6 各截面抗力Table6 SectionresistanceR1/kNR2/(kN·m)R3/kNR4/MPaR5/kNR6/MPa426379636894708526824126296

表6中:R1为主拱肋抗压承载力；R2为主拱肋抗弯承载力；R3为系杆抗拉承载力；R4为桥墩抗压强度；R5为桥墩抗剪承载力；R6为边拱的抗压强度。

3.5 构件可靠度计算与结果分析

构件的可靠度计算过程中，桥墩选取受力最不利的边拱侧桥墩做为研究对象。对于主拱关键截面受弯和受压均以拱脚最不利，因此，此处对于主拱仅示出了主拱拱脚的可靠度变化情况。计算结果如图7所示，其中L代表系杆索力损失。

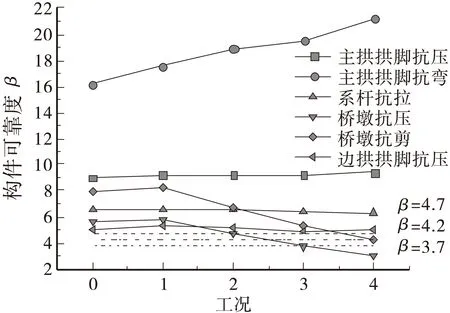
图7 不同构件β随工况变化Figure 4 Reliability variation of different components along with different replement schemes

依据文献[3]中对桥梁结构构件在设计基准期100 a内的目标可靠度指标β0的要求，分析构件可靠度β随不同工况的变化规律，可得以下结论：

主拱肋可靠度较高，其次是系杆可靠度，均大于4.7，满足一级安全等级的要求。

对于桥墩抗剪，在各工况下，其可靠度在4.3～7.9之间变化，在工况3以前，均满足一级安全等级的要求，在工况4情况下，可满足二级安全等级的要求。

对于桥墩抗压，在各工况下，墩底最不利，工况0时，其可靠度为4.3，工况1时，由于限载，可靠度增加至4.6，均满足二级安全等级的要求；工况2时，其可靠度减小至3.9，满足三级安全等级的要求，工况3及工况4，可靠度进一步下降，不能满足三级安全等级的要求。

3.6 体系可靠度计算结果分析

对于主拱肋抗压及抗弯失效模式中，拱脚、拱梁结合处、1/4主拱、拱顶4个失效状态下拱脚最不利，因此选择拱脚失效作为主拱肋失效的代表模式；对于桥墩墩顶及墩底截面，墩底最不利，因此选择墩底失效作为桥墩失效的代表模式。

将各种情况下的构件失效模式按可靠度指标β右小到大排列，见表7，并计算各失效模式的相关系数，此处仅示出了工况0时的构件失效可靠度情况及相关系数(见表8)。

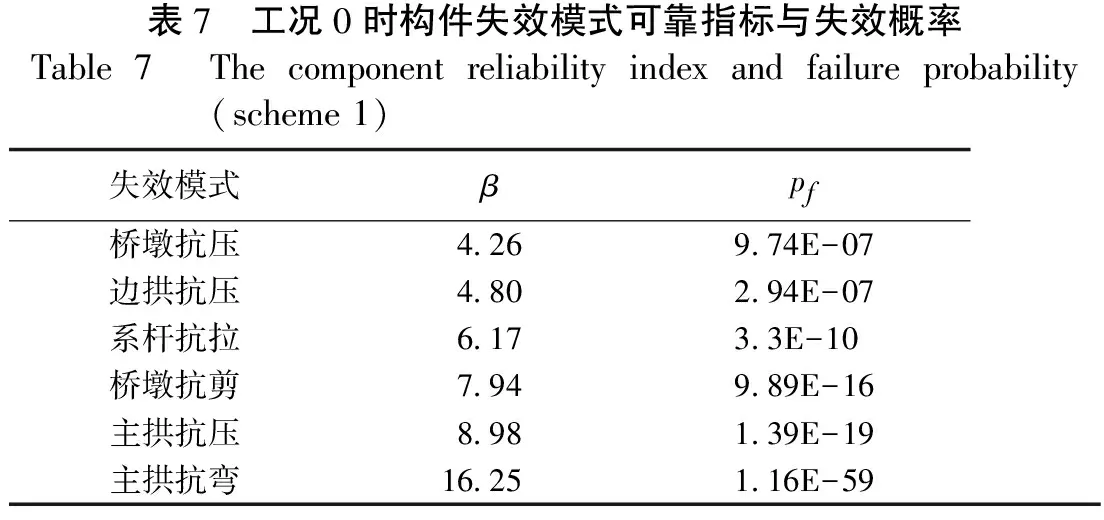
表7 工况0时构件失效模式可靠指标与失效概率Table7 Thecomponentreliabilityindexandfailureprobability(scheme1)失效模式βpf桥墩抗压426974E-07边拱抗压480294E-07系杆抗拉61733E-10桥墩抗剪794989E-16主拱抗压898139E-19主拱抗弯1625116E-59

表8 工况0时各失效模式的相关系数ρTable8 Correlationcoefficientofeachfailuremodescheme1)失效模式主拱抗压主拱抗弯系杆抗拉桥墩抗压桥墩抗剪边拱抗压主拱抗压100093099099097100主拱抗弯093100088095097093系杆抗拉099088100098094099桥墩抗压099095098100099099桥墩抗剪097097094099100097边拱抗压100093099099097100

将上述失效模式与相关系数代入PNET法中进行结构体系可靠度计算，假设相关系数界限值ρ0=0.8，结果见图8。

图8 不同工况下结构体系可靠度变化Figure 8 Reliability variation of system along with different replement schemes

依据文献[5]对桥梁结构体系在设计基准期100 a内的目标可靠度指标β0的要求，分析结构体系可靠度随不同系杆更换方案变的化情况可知：

工况0时，其可靠度为4.3，工况1时，由于限载，可靠度增加至4.6，均满足二级安全等级的要求；工况2时，其可靠度减小至3.9，满足三级安全等级的要求；工况3，其可靠度减小至2.9，不能满足三级安全等级的要求；工况4，可靠度进一步下降，减小至2.2，不能满足三级安全等级的要求。

4 结论

本文依托某跨径跨布置为46 m+202 m+46 m柔性系杆飞燕式钢管混凝土拱桥为工程背景，以系杆索力损失10%为初始状态，提出了4中不同系杆更换方案(单侧同时更换1根、2根、3根、4根，上下游侧同时进行更换)，基于有限元分析及系杆拱桥可靠度理论，研究系杆拱桥构件及体系随不同工况的可靠度变化规律。主要结论如下：

① 采用一次二阶矩法(JC)法分析主要构件可靠指标度随不同工况的变化情况，结果表明：各主要构件中桥墩墩底抗压最不利，工况0和工况1下，满足二级安全等级的要求；工况2时，其可靠度减小至3.9，满足三级安全等级的要求，工况3及工况4，可靠度进一步下降，不能满足三级安全等级的要求。

② 采用PNET法分析系杆拱桥结构体系可靠度指标随不同工况的变化情况，结果表明：工况0、1下，桥梁体系可靠度满足二级安全等级的要求；工况2时，满足三级安全等级的要求；工况3、4，其可靠度分别减小至2.9、2.2，不能满足三级安全等级的要求。

综上所述,方案1、2均可行，方案1施工步骤较繁琐，方案2能够保证桥梁的最低安全等级，同时尽可能缩短施工时间。建议采用方案2进行系杆更换。

[1] 陈宝春. 钢管混凝土拱桥 [M]．北京：人民交通出版社，2007.

[2] 王文涛. 斜拉桥换索工程[M]．北京：人民交通出版社，2006.

[3] 包琪,许纯梅.混凝土桥梁耐久性环境因素及其防护涂料分析[J].森林工程,2015,31(1):128-131.

[4] 孟令国,江瑞龄,祝争艳.桥面防水粘结材料的性能对比研究[J].森林工程,2016.32(3):73-75+80.

[5] GB/T 50283-1999, 公路工程结构可靠度设计统一标准[S].

[6] 张志.系杆拱桥结构构件可靠度评估研究[D].合肥：合肥工业学院，2013.

[7] 兰维勇. 既有斜拉桥拉索索力有限元分析及试验研究[D]. 长沙：中南大学，2013.

[8] 郑怡, 刘明，高飞,等. 一种新的既有受弯构件时变可靠度计算方法[J]. 公路工程，2008,23(5): 32-35

[9] 骆佐龙, 董峰辉. 连续梁桥悬臂施工状态可靠度分析[J]. 公路工程，2013,38(3):162-164.

[10] 张明. 结构可靠度分析-方法与程序[M]．北京：科学出版社，2009.

[11] Rackwitz R, Fiessler B. Structural reliability under combined random load sequences[J]. Computer & Structures,1978, 9(5): 489-494.

[12] Feng Y.S. A method of computing structural system reliability with high accuracy[J]. Computer & Structures, 1989, 33(1):1-5.

[13] 梁雄. 斜拉桥拉索腐蚀行为及使用寿命预测研究[D]. 重庆：重庆交通大学，2008.

[14] 项海帆. 高等桥梁结构理论[M]．北京：人民交通出版社，2001.

[15] JTG D62-2004， 公路钢筋混凝土及预应力混凝土桥涵设计规范 [S].

[16] DBJ/T 13-136-2011，钢管混凝土拱桥技术规程[S].

Replacent Scheme Analysis of Flexible Tied Bar Based on Reliability Theory

TANG Hui1, CUI Xiupneg2, GAO Yanmei3, ZHOU Zhixiang3,4

(1.CCCC Road and Bridge Consultants Co．，Ltd．，Beijing 100011， China; Beijing Zhongjiao Hualian Technology Development Co.,Ltd., Beijing 100101, China; 3.Chongqing Jiaotong University, College of civil engineering, Chongqing 400074, China; 4.State Key Laboratory Cultivation Base of Mountain Bridge and Tunnel Engineering, Chongqing 400074, China)

Flexible tied bas is the key structure of arch bridge, which prestress loss has an important impact on the reliability of bridge, to find out a resonable replacing sechem, this paper relies on a concrete filled steel tube flexible tied arch bridge with span arrangement of 46 m+ 202 m+46 m as the engineering background, assume 10% prestress loss as the initial state, 6 replacement schemes are put forward. By using JC and PNET method, the reliability changes of the bridge is analyzed under each scehmes. Results show that scehme 1 and 2 are excutable, scheme 2 can shorten the construction time and ensure the safety, which makes it the final scheme.

flexible tied bar; replacement scheme; reliability

2015 — 04 — 13

科技部973计划(国家重点基础研究发展计划项目2012CB723300)

唐 辉(1990 — )，男，四川广安人，硕士，助理工程师，主要从事钢混组合桥梁研究及设计。

U 445.4

A

1674 — 0610(2016)06 — 0029 — 07