2016年高考数学四川卷理科第10题探究*

☉四川师范大学数学与软件科学学院 李雪梅☉内江师范学院数学与信息科学学院 赵思林

2016年高考数学四川卷理科第10题探究*

☉四川师范大学数学与软件科学学院 李雪梅☉内江师范学院数学与信息科学学院 赵思林

2016年高考数学四川卷理科第10题：在平面内，定点A，B，C，D满足动点P，M满足则的最大值是（ ）.

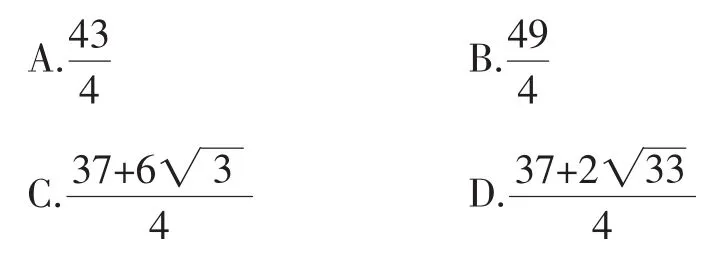
此题立意鲜明，含有教材背景，思路宽解法多，极富思维价值，许多一线教师对此题给予较高评价.下面拟从试题的立意分析、教材背景、思路与解法探究、试题的推广、解题后的回顾与教学启示等方面作一番研究.

一、试题的立意分析

立意是试题的考查目的.高考数学命题以能力立意为价值取向，一般从数学语言、数学知识、数学思想方法、数学能力素养等方面确定试题的考查目的.本题重视对数学能力和数学素养的考查［1］.下面从考查数学语言、数学思想方法、数学能力素养等方面分析该题的立意.

以数学语言立意：数学语言主要包括抽象的符号语言、直观的图表语言、量化的代数语言和普通的自然语言，这里的自然语言是指母语，在中国母语指汉语.本题以6个点（4个定点和2个动点）、向量的模、向量的数量积、向量的线性关系、向量的模的平方、多个方程等符号的形式呈现，考生普遍感到字母多、符号多、关系多，颇有无从下手、力不从心的心境.面对比较多的向量符号，一种自然的考虑是用向量自身的知识和方法解决问题，这对向量掌握得不好的考生来说是困难的.因此，更多的考生是选择将抽象的向量符号语言转化为直观的图形语言或代数语言（如坐标语言）.这显然有考查数学语言的相互表征与互译互化的意图.

以数学思想方法立意：本题若只用向量自身的知识和方法解决，则需用向量法；本题若不用向量法，则可考虑先建立直角坐标系（坐标法），然后用三角法或解析法解决问题.如果从条件和问题的几何意义来思考和处理问题，运用数形结合思想，则可用平面几何知识和方法直接简洁解答.因此，本题的解答可以涉及4大基本方法：向量法，坐标法，三角法，解析法；也必涉及求最值的一些方法.本题考查了数形结合、化归与转化等思想.

以数学能力素养立意：该题考查了考生的思维能力、运算能力、实践能力（动手画图）和创新意识.数学能力素养的核心是思维.本题对思维能力进行了全面考查，对众多数学符号的观察与联想，对解题思路的预估与顿悟，对解题方法的尝试与选择等，都需要直觉思维；对正三角形的判定、正三角形边长的计算的线性表示、最值的计算等，则需逻辑思维；对隐藏在题目中的几何本质的深邃洞察与灵活运用，则需灵感思维和创新思维.本题还考查了思维的广阔性、深刻性、灵活性、独创性等品质.

二、试题的教材背景

从历年高考试题的题源来看，教材是试题的主要来源，是高考命题的重要依据和出发点，很多优秀的高考试题都有“源于教材、高于教材”的特点.本题源于教材、高于教材.如题干中的是以人教A版《普通高中课程标准实验教科书》必修4第二章总复习题B组的第5题和第8题为背景改编的.题干中动点P，M满足含有人教A版必修2第4.1.2节的例5的背景，这个例5可以推广成一个命题：平面内，圆上任意点与一个定点连线的中点的轨迹仍是一个圆.像这样立足于教材设计的试题，既可保证试题背景的公平性，又对抑制题海战术有好处，还对中学数学教学有良好的导向作用.因此，应大力提倡立足于教材编拟高考试题.

三、思路与解法探究

乔治·波利亚在《数学的发现》序言中说：“掌握数学就意味着善于解一些要求独立思考、思路合理、见解独到和有发明创造的题.”思维心理学认为，发散思维是创造性思维的核心.本题具有思路宽阔、解法多样等特点.本题可以从多种不同角度进行分析与探究，可以得到多种解法，这可培养学生的发散思维，从而可以培养学生的创造性思维.

思路（一）：三角法

同理可得，DA⊥BC，DC⊥AB，从而D是△ABC的垂心.

所以△ABC的外心与垂心重合，因此△ABC是正三角形，且D是△ABC的中心.即

如图1，以A为原点、直线SA为x轴建立直角坐标系.

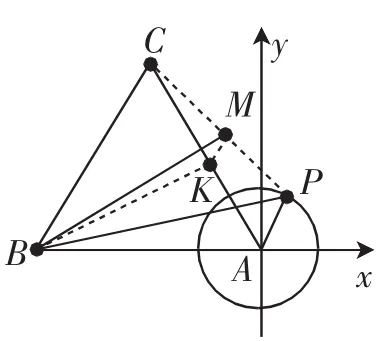
图1

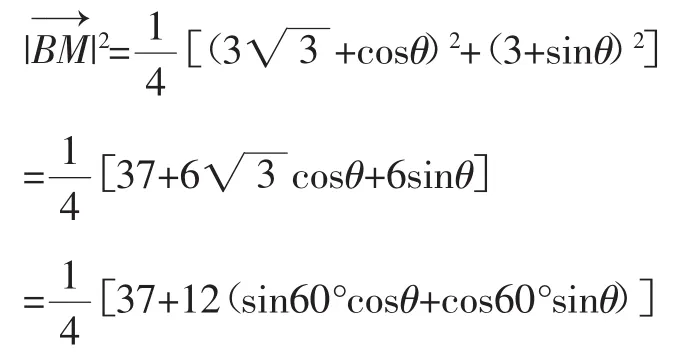
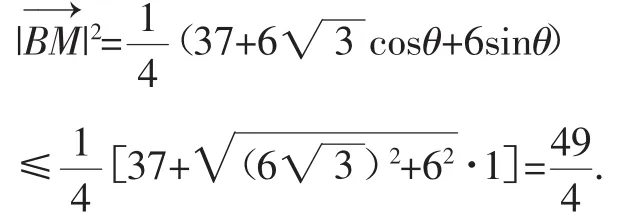
思路（二）：解析法

设点P（x，y），则点P的轨迹方程为x2+y2=1，因为点M是PC的中点，则M的坐标为

又设M（x1，y1），则可得代入可得：即这表明，点M在圆

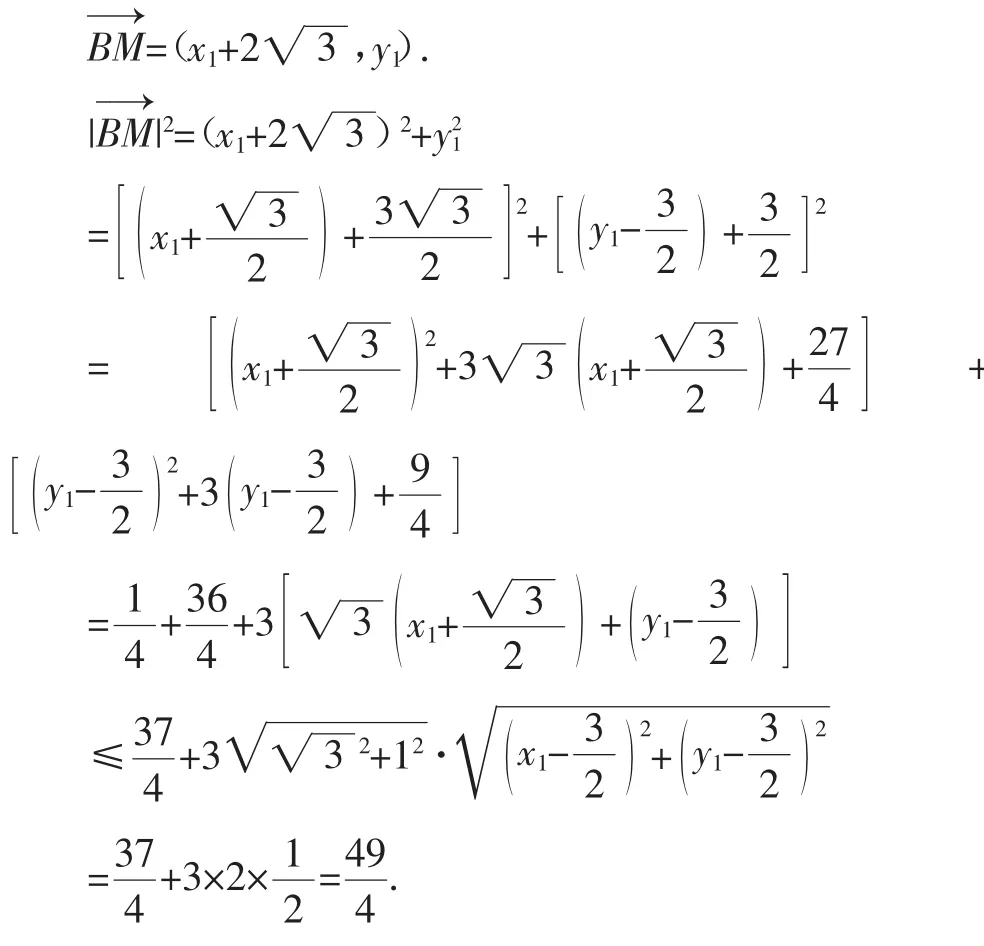
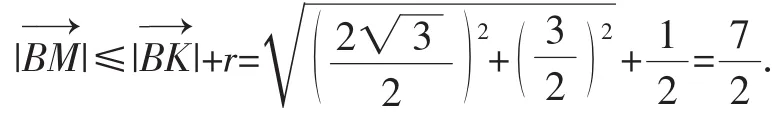
思路（三）：向量法

方法6：取AC的中点K，连接KM，BM，BP，BK.

因为点M是PC的中点，因此有

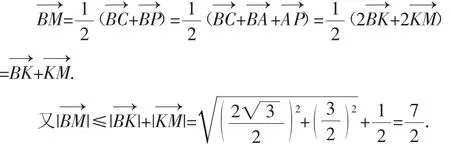
点评：此解法充分发挥了向量的工具性作用，解过程体现了思维量大、运算量小的特点.

思路（四）：平面几何法

方法7：设AC的中点K，连接KM，BK.KM是△ACP中位线，则即其中K为定点，M为动点，动点M到定点K的距离恒等于这表明动点M的轨迹是以K为圆心为半径的圆当且仅当B，K，M三点共线且K在B、M之间时取等号.故

点评：此解法深刻洞察并发掘了隐藏在题目中的几何本质（动点M的轨迹是圆），显示出几何直观在数学解题中的巨大价值，值得欣赏和提倡.

四、试题的推广

试题的推广是指对试题进行引申、加强与深化.对试题的推广，有利于促进学生认知的深化，开拓思维的视野，并能培养学生发现问题、提出问题、分析问题和解决问题的能力，以及培养学生的数学探究意识和创新意识［2］.数学问题的推广，对培养学生的观察洞察能力、类比联想能力、归纳猜想能力、问题探究能力是有益的.

下面我们对该题进行推广.

推广1平面内的定点A，B，C，D满足空间中的动点P，M满足则的最大值是（ ）.

推广1将平面内的动点P，M推广到空间中的动点，仍可用前面的一些解法得出答案，且的最大值不变.

推广2平面内，定点A，B，C，D满足动点P，M满足则的最小值是（ ）.

推广3平面内的定点A，B，C，D满足动点P满足0），动点M满足则的最大值是（ ）.

五、解题后的回顾与教学启示

上面的思路探究与解法运用了数形结合、化归与转化等重要的数学思想，并运用了三角法、解析法、向量法、平面几何法等多种数学基本方法，有效训练了数学思维的灵活性、发散性、选择性和创造性.此外，解答本题有以下几个关键点：一是数学语言间的转换，即要准确的将符号化的向量语言转化为直观的图形语言或代数语言（如坐标语言）等；二是运用教材习题的解题经验，准确并快速地判断△ABC为正三角形；三是本题以A，B，C，D等点为原点建立直角坐标系都是可行的，因此建系具有灵活性，但建立不同的坐标系，其运算量的大小不同，本题以点A为原点建立坐标系较为理想，可以减少运算量，简化求解过程；四是灵活运用数学思想方法，可以达到多想少算的效果，比如用向量法，或者用数形结合思想（平面几何方法），就能回避或减少烦琐运算.

此题对教学的启示是多方面的：（1）不管是新课教学还是高三复习，都应重视教材中的例题、习题、复习题的研究，这里主要是指对教材中部分富含思维价值的题目进行研究；（2）教学中应重视抽象的符号语言、直观的图表语言、量化的代数语言、熟悉的自然语言之间的相互表征与互译互化；（3）应重视数学思想方法的教学；（4）数学解题教学要突出“想”的训练，包括多角度地联想、大胆地猜想、直觉地想象等；（5）大力提倡立足于教材编拟高考题，唯有如此，才能真正使高中数学教学重视教材、回归教材、研究教材［3］.

1.张进华.既要夯实“通性通法”，又要学会“灵活变通”——从两道高考试题的解法谈起［J］.中学数学（上），2016（5）.

2.赵思林.高考数学解题分析［M］.成都：四川大学出版社，2011.

3.赵思林，李建军.一个高考最小值问题的研究［J］.中学数学研究，2012（5）.

*项目来源：教育部“本科教学工程”四川省地方属高校本科专业综合改革试点项目——内江师范学院数学与应用数学“专业综合改革试点”项目（ZG0464）；四川省“西部卓越中学数学教师协同培养计划”项目.赵思林系硕士研究生李雪梅的指导教师.赵思林系本文通讯作者.

1.李雪梅，女（1994-），四川师范大学数学与软件科学学院，学科教学（数学）专业硕士研究生.

2.赵思林，男，（1962-），教授，硕士生导师，主要从事数学教育、高考数学和思维心理学研究.