COMSOL的加气混凝土热湿耦合传质模拟分析
2017-01-12韩晓烽王友辉
韩晓烽,王友辉,徐 旭
(中国计量大学 计量测试工程学院,浙江 杭州 310018)
COMSOL的加气混凝土热湿耦合传质模拟分析
韩晓烽,王友辉,徐 旭
(中国计量大学 计量测试工程学院,浙江 杭州 310018)
采用COMSOL Multiphysics软件进行多孔介质加气混凝土的热湿耦合数值模拟研究.采用双驱动势和优化参数结合的模拟方案,对控制方程进行推导.通过对文献结果的对比,验证了该模型的可行性.模拟分析了环境温度、时间等因素对加气混凝土样品的湿迁移影响,随时间的增加湿传递速率减缓;5~15 ℃时湿传递速率缓慢,温度的影响较大,15~30 ℃时湿传递加快且速率保持一致.因此,在干燥环境下,加气混凝土墙体温度低于15 ℃以下可有效减少外界湿传递.
热湿耦合;多孔介质;数值模拟
我国建筑能耗占社会总能耗的26%且呈稳定增长趋势[1],每年新增建筑面积达到20亿m2.至2030年建筑能耗总量将增加一倍以上[2].因此通过研究建筑围护结构的能量传递,减少能量损失,从根本上提高建筑围护结构的节能效率势在必行.
目前在围护结构热湿耦合传递的理论分析和实验研究方面[3-5]已取得一些成果.陈友明等[6]实地测试了长沙热湿地区1月份和7月份的墙体内部的温湿度变化,分析了环境等对热湿传递的影响;Rafidiarison等[7]使用双气候实验箱模拟复杂的震荡及周期型边界条件,研究了规律性边界下的热湿耦合情况.Bear等[8]结合经典运输理论与空间平均定律提出了多孔介质中热湿耦合传递的多相运动方程和能量方程.郭兴国[9]在Budaiwi模型的基础上,考虑相变以及墙体内部液态水传递并将空气含湿率看作是材料含湿量和温度的函数,建立了多层墙体热湿耦合传递模型然后采用有限容积法对方程组进行求解.Belleghem[10]使用BES模型和CFD模型对建筑围护结构进行了数值模拟,并设计了一个等温边界实验台用以验证CFD-HAM和BES-HAM两种模型.
国内外学者们对热湿传递过程进行了大量系统的研究,相比实验研究,数值模拟具有快速、成本低廉等优点.但在数值模拟中由于微分方程耦合过程出现的参数复杂多样,难以收敛仍存在耗时长、精度不高等问题.为此,针对已有的模拟方案中的不足,本文基于数值模拟工具COMSOL软件,提出一种对多孔建筑材料热量、湿份和空气同时耦合的控制传递方程改进方案,减小了数值模拟耗时和参数多等困难,从而提高了实际工程应用中的效率.
1 控制方程及简化
建筑围护结构的热湿动态响应对室内空间的湿度状况和建筑的能耗有着巨大的影响.为了准确地捕捉建筑围护结构对室内环境和暖通制冷空调系统的影响,建立一个瞬态热、湿、空气的耦合模型来处理热量和水分的传递是至关重要的.图1展示了围护结构多孔材料的能量关系图.本文经由基础传递理论和Fick和Darcy定律推导出热湿空气在墙体内部的瞬态耦合传递控制方程.通过对驱动势的改进和对方程项的简化,以及焓值的运用,来提高方程在实际应用中的可行性和实用性.

图1 多孔材料的能量关系图Figure 1 Energy relationship of porous materials
1.1 湿平衡方程
在多孔材料的孔隙中,水分是以气态或液态的形式进行质量传递的.根据理论公式可以得到气体和液体的运动规律为方程(1)和(2).依据这两个方程可以导出水分在材料中流动的运动情况(3).

(1)
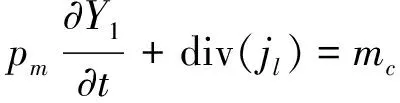
(2)

(3)
其中:ρm为材料密度,kg/m3;Yv为水蒸汽质量分数;V为气流速度,m/s;Yl为液态水质量分数;mc为水分冷凝/蒸发率,kg/s;jv为蒸汽扩散项;jl为液体传递项.
根据菲克和达西定律改写(3)中各项可以得出水分平衡方程[11]:


(4)
式(4)中:ω为绝对湿度,kg/m3;φ为相对湿度;Pv为蒸汽压力,Pa;Psuc为吸入压力,Pa;δv为蒸汽渗透率,m/s;krg为蒸汽相对渗透率,m/s;ρv为水蒸汽密度,kg/m3;μ为空气动力粘度,Pa·s;ρω为液态水密度,kg/m3;Pg为气体总压力,Pa.
方程(4)是由各种水分驱动势能组成,具体为:ω,φ和Psuc等.这些驱动势能和与其相关的梯度项,都可以由一个单一的流动势能来表示.在本文中所选择的这个流动势是相对湿度(φ),因为与不连续的水分含量相比,它具有在不同的水分存储性能(吸收和保湿)的双层材料的交界面连续变化的性质.因此通过keleve方程,理想气体方程和菲克达西定律等对方程(4)进行转换.得出改良后的湿平衡方程:

(5)
式(5)中:θ为吸附容量,kg/m3;P为饱和蒸汽压力,Pa;ρa为空气密度,kg/m3;Cc为自定义符号,0.622/pa;Dl为液体渗透率,m/s.
1.2 热平衡方程
内能和焓h的守恒方程能够从总储能的守恒方程中推导得出.系统总储能(E)是内能(U),动能(KE),势能(PE)的总和,E=U+KE+PE.总存储能的守恒方程能够通过考虑控制体积和控制体积中的储能变化率(等式左侧第一项)、控制体积中对流进出的能量(等式左侧第二项)、扩散项(等式左侧第三项)也就是外部因素在控制体积表面做的功包括黏滞力和重力(自身),热源(或冷源)(等式右侧,Q)来得出,得出如下方程[12]:

(6)
式(6)中:e为每单位质量所含能量,J/kg;ρe是每单位体积所含能量,J/m3.
为模拟计算的准确与快捷,使用混合焓h(水分、空气和固体基质)重写瞬态项、对流和扩散项,改良后的热传递方程为
div(-λeffgrad(T))=mchfg+
mcT(Cpv-Cpl)+Q.
(7)
式(7)中:Cpeff为有效热容,J/(kg·K);λeff为有效导热系数,W/(m·K);ρm为干材料密度,kg/m3;Cpa为空气比热容,J/(kg·K);Cpv为水蒸汽比热容,J/(kg·K);Cpl为液态水比热容,J/(kg·K);hfg为冷凝/蒸发潜热,J/kg.
1.3 空气平衡方程
通过围护结构墙体材料内部的空气流动能够通过Poiseuille(泊肃叶)定律描述,等式与流速的压力梯度有关,下面给出空气传递时的质量平衡方程[13]:

(8)
在建筑物理应用过程中,空气被认为是不可压缩的.这是因为实际过程中空气通过孔隙时具有非常低的流速、较低的压力和较低的温度变化的性质.因此,根据以上特性能够给出空气传递时的动量平衡方程:
div(ρaV)=0.
(9)
结合质量平衡方程等式(8)和动量平衡方程等式(9)给出本文计算气流通过围护结构时的速度公式:
-div(δadiv(P))=0.
(10)
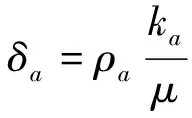
2 方法验证
本次模拟采用COMSOL软件中系数型偏微分方程PDES模式进行求解,使用内置求解器得出数据结果.与文献Hagentoft[13]等人使用HAM计算方法的结果进行对比分析.计算对象为一块200 mm厚的均匀墙体,首先将材料加湿到95%左右,然后将上下表面分别暴露在相对湿度为45%和65%的环境中,温度保持20 ℃不变,分析物体随时间变化内部水分干燥的变化情况.在计算过程中采用的材料热物性参数参见文献[13].在干燥时长分别为100 h,300 h和1 000 h的时候将本次模拟结果与文献中的结果进行比较,如图2.
由图2可见,随着时间的推移,湿度从两侧逐渐传递进入周围环境.在大约300 h时,墙体中心位置的水分含量开始受到外界环境影响并逐渐降低.在本次模拟中,从图2可以看出COMSOL得出的数值解结果基本与文献中的解析解数据基本吻合,由此可以初步证明在上章节中推导得出的平衡控制方程的准确与可行性.

图2 模拟结果与解析解对比图Figure 2 Comparison of simulation result and analytical solution
3 模拟分析
3.1 模拟对象及参数
本文基于COMSOL软件对不同温度下B04级蒸压加气混凝土的湿迁移进行热湿耦合模拟分析.经由控制方程转换过后的软件方程需要用到一些常用参数和根据测试材料不同而不同的变量参数.以下是根据湿平衡方程(5)与热平衡方程(7)给出的需要使用到的固定参数,如表1,表2.

表1 湿传递所需参数Table 1 Parameters in moisture transmission

表2 热传递所需参数Table 2 Parameters in thermal transmission
确定模拟材料的相关参数.将B04级蒸压加气混凝土,加工成尺寸为100 mm×100 mm×250 mm的长方体,内部干燥成相对湿度为1%.样品不参与传热的四个面绝湿(此时湿传递可以视为一维传递),并对材料相关物性参数进行文献查找与实际测量,得出数据如表3.

表3 B04级加气混凝土物性参数Table 3 Physical parameters of B04 concrete
根据表1、表2、表3以及上文推导得出的热湿空气耦合控制方程,即可对不同温度下B04级蒸压加气混凝土的湿迁移进行热湿耦合模拟分析,得出样品内部温湿度分布情况.将加气混凝土左右端面相对湿度分别设为90%、1%,以此湿度差为驱动势,模拟加气混凝土内部的一维湿传递.模拟情况如图3.

图3 模拟情况简图Figure 3 Simple picture of simulation
3.2 模拟结果分析
当模拟环境温度为5℃时,依次在第24 h、第48 h、第72 h、第96 h和第120 h各生成一条试样内部相对湿度分布曲线,如图4所示.从图4中可以看出从左侧相对湿度90%处到右侧1%,随着距离的增加湿度逐渐降低.在左侧湿度变化比较明显,而右侧湿度的变化较为缓慢.当时间为24 h时,距离左侧0.061 m的地方相对湿度达到5%.48 h、72 h、96 h和120 h等曲线的变化趋势类似,但是相对湿度达到5%的距离逐渐增加,分别为0.084 m、0.102 m、0.116 m和0.127 m,这说明随时间的增加,水蒸气逐渐向右边传递,传递速度逐渐减缓,平均传递速度为6.88×10-4m/h.

图4 内部相对湿度分布(5 ℃)Figure 4 Internal relative humidity distribution(5 ℃)
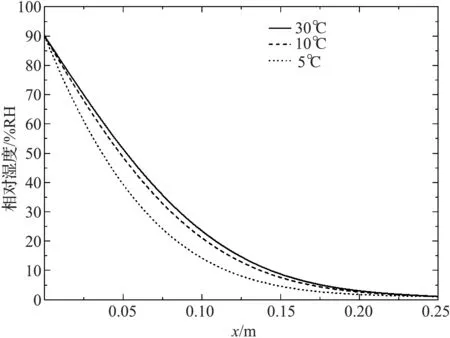
图5 第168 h内部相对湿度分布(5 ℃、10 ℃和30 ℃)Figure 5 Internal relative humidity distribution after 168 h (5 ℃、10 ℃和30 ℃)
图5模拟了温度为10 ℃、30 ℃时加气混凝土经过168 h后内部的相对湿度分布情况.由图可见,5 ℃环境下湿度传递较为缓慢,168 h后0.1 m处的相对湿度为14.17%,而10 ℃与30 ℃环境中,168 h后0.1 m处的相对湿度就已经达到了21.06%和23.45%.10 ℃与30 ℃环境下湿度分布曲线相差较小.温度越高,湿度传递越快,湿度分布曲线密集的越早.并且,随着时间的推移,湿度差慢慢减小,传递速率也会越来越慢,直到到达稳态,速率为零.
为了更直观地表现温度对加气混凝土内部湿迁移带来的影响,本文研究了在混凝土试样传递距离0.2 m处相对湿度从1%上升到5%所耗时间,如图6.

图6 不同温度下0.2 m处相对湿度上升到5%所需时间Figure 6 Time needed for up to 5% relative humidity under different temperature at 0.2 m
由图6可以看出,5℃环境下用时最长,为498 h,而在15 ℃、20 ℃、25 ℃、30 ℃环境下,所需时间几乎相同,在226 h左右,相差最大为8 h,由此说明,在5 ℃到15 ℃之间,湿传递缓慢,且温度对湿传递速率的影响较大,在15 ℃到30 ℃之间,湿传递略快且速率基本保持一致,几乎不再受温度的影响.该结论与冯驰等人的研究结果相符[14].
所以,维持干燥环境时,温度降到15 ℃以下,加气混凝土墙体才可能有效隔绝外界湿传递.而在研究B04级加气混凝土的湿迁移状态时,研究环境温度在15 ℃以下,要着重考虑温度的影响,环境温度在15 ℃以上,在精度要求不高的情况下,温度的影响较为不明显.
4 小 结
建筑围护结构的热湿耦合传递模拟研究是减小建筑能耗的重要手段.本文提出一种基于COMSOL软件的热湿空气耦合控制方程的简化方法.该方法得到的模拟结果与相关文献相比,结果基本吻合.对B04加气混凝土热湿耦合传递的模拟结果表明:温度越高,湿度传递越快,湿度分布曲线密集的越早.在水蒸气传递过程中,速率逐渐减少.当温度处于15 ℃以下时对湿传递的影响较为明显,在15 ℃至30 ℃时则可忽略其带来的影响.为了进一步验证改良方程的准确性和适用性,可设计复杂环境的实验,通过对比来优化方程,实现更精准快捷的数值模拟.
(致谢:感谢浙江大学热工研究组在本论文数值模拟方面给予的支持)
[1] 林立身,江亿,燕达,等.我国建筑业广义建造能耗及CO_2排放分析[J].中国能源,2015(3):5-10. LIN Lishen, LIANG Yi, YAN Da, et al. Generalized building energy consumption in our country and the CO_2 emission analysis[J]. China Energy,2015(3):5-10.
[2] 张燕.中国建筑节能潜力及政策体系研究[D].北京:北京理工大学,2015. ZHANG Yang. China building energy saving potential and policy system research[D]. Beijing:Beijing Institute of Technology,2015.
[3] LYU Xiaoshu. Modelling of heat and moisture transfer in buildings: I. Model program[J]. Energy and buildings.2002,34(10):1033-1043.

[5] 易思阳,范利武,徐旭,等.多孔建筑材料水蒸气扩散系数的瞬态测试方法[J].浙江大学学报(工学版),2016(1):16-20,26. YI Siyang, FAN Liwu, XU Xu, et al. The transient text method of the water vapor diffusion coefficient in porous building materials[J]. Journal of Zhejiang University (liberal arts ed),2016(1):16-20,26.
[6] 陈友明,邓永强,郭兴国,等.建筑围护结构热湿耦合传递特性实验研究与分析[J].湖南大学学报(自然科学版),2010,37(4):11-16. CHEN YouMing, DENG Yongqiang, GUO Xingguo, et al. The transfer characteristic of heat and moisture transfer in building envelope[J]. Journal of Hunan University(JCR Science Edition),2010,37(4):11-16.
[7] RAFIDIARISON H, RéMOND R, MOUGEL E. Dataset for validating 1-D heat and mass transfer models within building walls with hygroscopic materials[J]. Building and Environment,2015,89:356-368.
[8] BEAR J, BACHMAT Y. Introduction to modeling of transport phenomena in porous media[J]. Kluwer Academic Publishers,1990,4:481-516.
[9] 郭兴国.热湿气候地区多层墙体热湿耦合迁移特性研究[D].长沙:湖南大学,2010. GUO Xingguo. The transfer characteristic of heat and moisture transfer of multi-layer wall building in warm and humid area[D]. Changsha: Hunan University,2010.
[10] BELLEGHEM M V, STEEMAN M, WILLOCKX A, et al. Benchmark experiments for moisture transfer modelling in air and porous materials[J]. Building & Environment,2011,46(4):884-898.
[11] SANTOS G H D, MENDES N, PHILIPPI P C. A building corner model for hygrothermal performance and mould growth risk analyses[J]. International Journal of Heat & Mass Transfer,2009,52(21,22):4862-4872.
[12] TARIKU F. Whole building heat and moisture analysis[D]. Montreal: Concordia University,2008.
[13] HAGENTOFT C E. HAMSTAD - Final report: methodology of HAM-modeling[D]. Goteborg: Chalmers University of Technology,2002.
[14] 冯驰.多孔建筑材料湿物理性质的测试方法研究[D].广州:华南理工大学,2014. FENG Chi. Study on the test methods for the hygric properties of porous building materials[D]. Guangzhou: South China University of Technology,2014.
Research on mass transfer for coupled heat and moisture through aerated concrete based on COMSOL
HAN Xiaofeng, WANG Youhui, XU Xu
(College of Metrology and Measurement Engineering, China Jiliang University, Hangzhou 310018, China)
Numerical simulation of coupled heat and moisture transfer in aerated concrete was studied by using Multiphysics COMSOL software. The control equation was derived by combining the double driving force and the optimization parameters. The feasibility of the model was verified by comparing with the results in literature. The influence of environmental temperature and time on moisture migration in aerated concrete samples was analyzed. The moisture transfer rate slows down with the decrease of temperature from 5 ℃ to 15 ℃, while between 15~30 ℃, moisture transfer becomes fast and the transfer rate keeps steedy. In a dry environment, the external moisture transfer can be effectively reduced when the temperature of the aerated concrete wall is less than 15 ℃.
coupled heat and mass transfer; porous media; numerical modelling
2096-2835(2016)04-0418-06
10.3969/j.issn.2096-2835.2016.04.011
2016-10-17 《中国计量大学学报》网址:zgjl.cbpt.cnki.net
国家自然科学基金资助项目(No.51378482).

TK122
A
