自适应MCM测量不确定度软件研发

陈超云，王 灿，文慧卿，汪濂泂，金 愿

(上海市计量测试技术研究院，上海 201203)

自适应MCM测量不确定度软件研发

陈超云，王 灿，文慧卿，汪濂泂，金 愿

(上海市计量测试技术研究院，上海 201203)

蒙特卡洛法(MCM)测量不确定度评定中模型复杂、计算量大，现有软件往往只在某一模型中适用，不同模型间相互独立，且评定结果缺少自适应过程.基于LabVIEW软件生成输入量X的伪随机数，对X概率密度函数(PDF)离散抽样，得到输出量Y的离散抽样值，进而设计了自适应MCM测量不确定度软件.本软件实现了常用模型数学公式的自定义，增强了软件的适用性，同时重点介绍了自适应增加样本量M的算法.通过JJF1059.2-2012规范中实例的计算，验证了软件在常用模型评定中的有效性.

自适应MCM；测量不确定度；LabVIEW软件；软件研发

在测量模型为线性，输入量X的PDF符合中心极限定理的不确定度评定中，GUM(不确定度指南)应用广泛.MCM作为GUM的增补方法，不受GUM评定条件限制，适用于测量模型非线性和PDF非对称的复杂模型评定[1-3].

目前有很多优秀的MCM软件，主要有基于Minitab，Matlab，Delphi，Crystal Ball以及Mircrosoft Excel的软件[4-6].但上述软件往往只针对某一特定模型适用，软件设计不具有普遍适用性，且抽样次数缺少自适应计算过程.因此，很难保证评定结果是否满足统计意义上的稳定[7].

本文基于LabVIEW软件设计了自适应MCM软件，通过产生X的伪随机数，最大支持8个不确定度分量，和8种PDF分布，实现常用测量模型的软件一体化.在自适应增加抽样次数编程算法中[8]，保持样本量M不变，增加循环次数的方式来增加离散抽样次数，将不确定度由输出量Y标准差过渡到输出量算术平均值的标准差.最终得到输出量Y的最佳估计值、标准不确定度以及包含区间等统计量[9-11].通过JJF1059.2-2012规范中实例的计算，验证了软件在常用模型评定中的有效性.

1 软件总体设计

自适应MCM评定测量不确定度软件设计结构如图1.

图1 软件设计结构Figure 1 Structure of the software

依据上述软件设计流程，自适应MCM软件总体分为五个模块：基本参数设置模块，输入量X设置模块，测量函数设置模块，输出量Y和自适应模块.

1)确定输入量X个数，本软件最大支持8个不确定度分量.

选取包含概率p，在规定数值容差δ下，取样本量M的最小量.

Mmin=1/(1-p)×104.

(1)

M在第一次循环选取MCM最低要求量，以便软件后续采用自适应判断输出量Y标准差稳定性，增加循环次数来提高M.

2)根据1)设置的X个数，调用对应X个数的子VI.设置不确定度分量的PDF，本软件支持：正态、均匀、t、三角、F、卡方、柯西和拉普拉斯8种分布类型.

3)建立Y和X的测量函数.

y=f(x1,…,xN).

(2)

针对单个软件只支持单个测量模型的情况，本软件调用公式解析字符串VI，自定义函数表达式，使软件适用于线性和非线性，对称和非对称PDF的模型计算.

4)定义变量s为LabVIEW循环次数.以算术平均值的标准差作为测量结果，因此Y的平均值为：

(3)

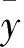
在多次循环测量中，Y的不确定度取多次循环测量的平均值.

(4)

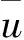
确定包含区间左右端点[ylow,yhigh].定义q和i为向下取整方式：

q=[pM+1/2],

(5)

i=[(M-q)/2+1/2].

(6)

如此定义可兼顾pM和(M-q)/2为整数和非整数两种情况，以提高编程的效率.此时ylow=y(i),yhigh=y(i+q).当Y的PDF不对称时，重新定义i*使得其左右端点差y(i*+q)-y(i*)≤y(i+q)-y(i)，其中i=1,2...M-q，可得最短包含区间[y(i*),y(i*+q)].

5)自适应增加循环测量试验次数.多数不确定软件只是满足M的最低要求，而忽视了测量结果是否满足统计意义的稳定.本软件引入数值容差δ，由公式(4)计算得不确定度u(y)表示为c×10l，其中c是n位十进制数，l是整数，n是u(y)有效位数，一般为1或2.则δ表示为

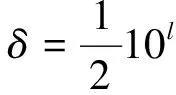
(7)

Y最佳估计值的算术平均标准差为

(8)

2 LabVIEW软件编程

以LabVIEW图形化语言作为本软件开发环境，具有友好的交互界面；其次LabVIEW在循环运算中具有快速的运算能力；最后LabVIEW的图形化编程方式，使研究人员无需过多考虑变量定义和子程序调用的编程，更好地把重点放在软件的数据流和算法程序上.

依据上述软件设计流程，分别介绍软件主程序和子程序模块.

2.1 主程序模块

软件主界面包括X的个数选取，包含概率p(95%、99%)选取，由p计算得初始M，s用于记录循环次数.输出Y的最佳估计值、标准不确定度、包含区间，及其PDF的直方图，主程序如图2.

图2 主程序框图Figure 2 Frame diagram of program

2.2 输入量X模块

输入量的不确定度分量支持8种PDF分布类型.将8种PDF封装为8个输入量子VI，通过设置输入量个数，调用对应的子VI，输入量VI的封装程序如图3.

图3 输入量VI图Figure 3 VI diagram of input quantity

确定好各输入量的分布函数后，由LabVIEW概率函数中“连续生成伪随机数VI”产生M个离散采样值,封装的PDF函数程序如图4.

图4 输入量PDF图Figure 4 PDF of input quantity

2.3 测量模型模块

确定X及其PDF的离散采样后，需要建立起Y和X的测量模型f(x).测量模型的特征参量与实际问题一致，将输入量PDF传递到输出量PDF.本软件实现输入模型数学公式的自定义，测量模型的数学公式程序如图5.

图5 测量模型公式Figure 5 Formula diagram of measurement module

由图5可知，自定义输入量的字符串变量，及数学公式.由“解析公式节点”函数，将X、Y字符串变量转换为浮点型变量；再由“解析公式字符串”函数，将解析后的离散抽样X通过数学公式计算得到Y的离散抽样值.

2.4 自适应模块

Y的离散抽样按递增次序排列，存入数组控件.在多次重复循环测量中，抽样值采用“连接”方式存入上一数组而不覆盖原来的数据.

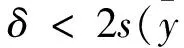
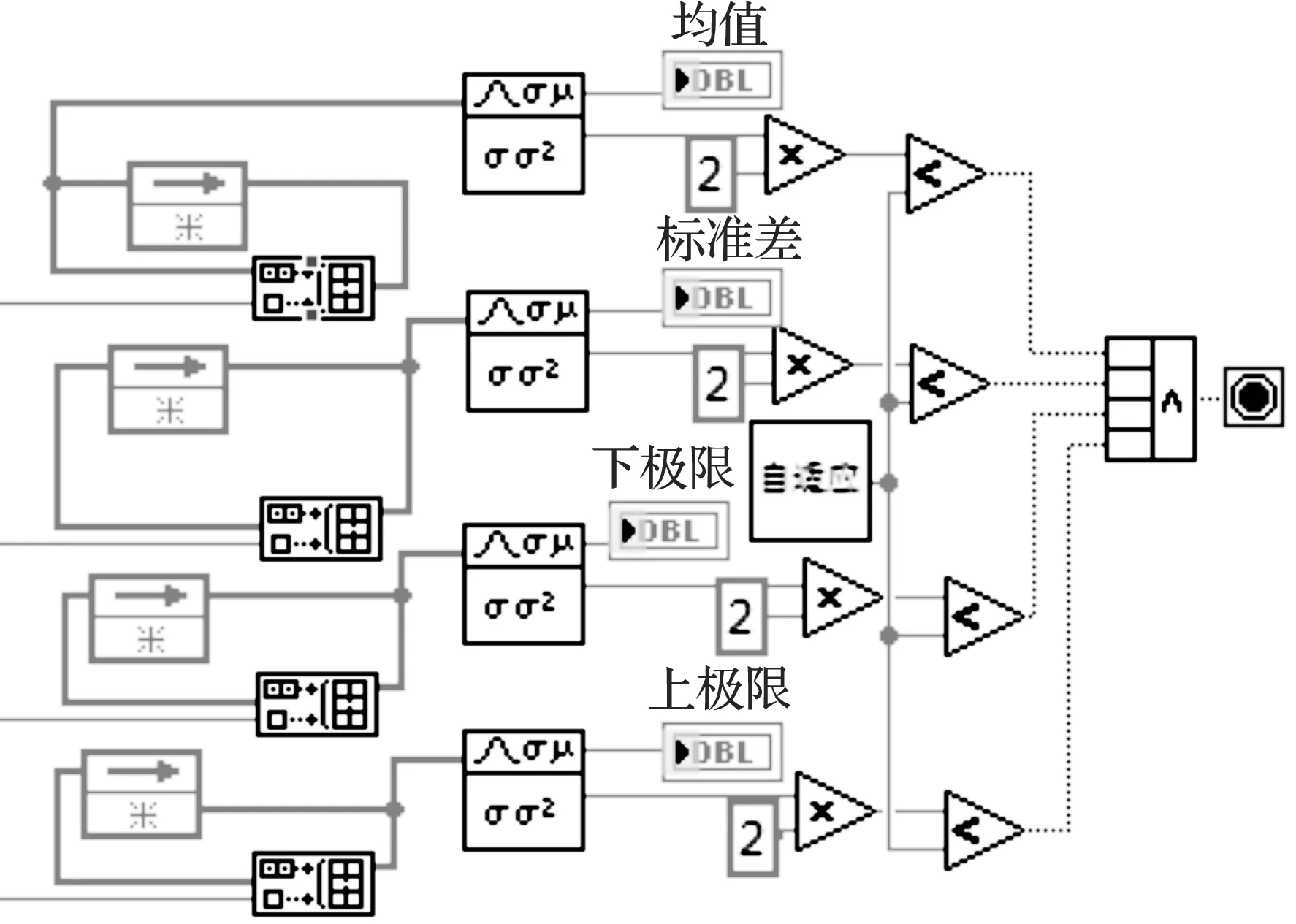
图6 自适应模块Figure 6 Adaptive module

3 实例验证

以JJF1059.2-2012《用蒙特卡洛法评定测量不确定度》规范中的实例来验证软件的有效性.

3.1 质量校准

砝码质量校准的测量模型如下：

(9)

式(9)中ρa0为1.2 kg.m-3，mnom为标尺质量100 g.由模型函数确定质量校准的输入量为砝码R折算质量mRC，配重小砝码质量δmRC，空气密度ρa，砝码W质量密度ρw和砝码R质量密度ρR.

根据模型的不确定度分量，设定砝码质量校准模型的PDF如表1.

表1 质量校准模型的PDFTable 1 PDF of quality calibration model

砝码质量校准有5个不确定度分量，选取区间概率为95%，则第一次循环默认M为20×104次，软件自动计算Y，直到满足自适应数值容差的要求.

经过3次循环自适应运算，总抽样数为60×104，得到数值容差δ和Y的4个输出量的2倍标准差如表2.

表2 数值容差与2倍标准差Table 2 Tolerance and 2 times standard deviation

满足自适应δ的要求，计算结果满足统计意义的稳定.将软件计算结果与GUM结果进行比较，对比数据如表3.

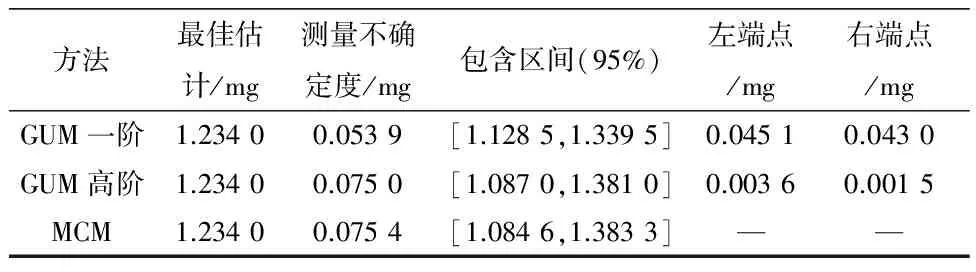
表3 质量校准模型计算结果比较Table 3 Comparison of calculation results of quality calibration model

3.2 量块校准

量块校准的测量模型如下：

δL=Ls+D+d-Ls[δa(θ0+Δ)+asδθ]-Lnom.

(10)

式中Lnom为标称长度50 mm.由模型函数确定量块校准的输入量为Ls、D、d、δa、θ0、Δ、as、δθ.

根据模型的不确定度分量，设定模型X的PDF，如表4.

表4 量块校准模型的PDFTable 4 PDF of gauge block calibration model

量块校准有8个不确定度分量，选取区间概率为99%，经过自适应运算，总抽样数为106，得到Y的计算结果，并与GUM结果进行比较，对比数据如表5.

表5 量块校准模型计算结果比较Table 5 Comparison of calculation results of gaugeblock calibration model

质量校准、量块校准计算结果表明：MCM软件与规范中GUM获得的结果具有较好一致性，但是在非线性模型中，MCM软件与一阶GUM的不确定度存在显著不同.由于非线性模型难于求偏导，对于一阶GUM来说，不确定度结果偏小，显然计算结果被高估了.只有在高阶GUM下两者的结果基本一致.基于LabVIEW软件编写的自适应MCM软件计算得结果与规程中高阶GUM所提供的结果基本一致，验证了软件的有效性.

4 结 语

基于LabVIEW设计了常用模型的自适应MCM测量不确定度计算软件.本软件界面简洁、操作简单，实现常用模型数学公式的自定义输入，适用于一般工业的不确定度计算.特别是设计了自适应增加样本量M的算法，提高了计算结果的准确性.通过实例计算，表明本软件能快速、准确地计算测量不确定度，同时也为不确定度软件的研发提供一种编程思路.

[1] 朱鹤年,肖志刚,朱美红,等.温度计修正值不确定度评定方法的改进研究[J].中国计量学院学报,2014,25(4):344-348,423. ZHU Henian, XIAO Zhigang, ZHU Meihong, et al. On the improvement of the uncertainty evaluation method for the correction of thermometer calibration[J]. Journal of China University of Metrology,2014,25(4):344-348,423.

[2] 廉育英.容量计量技术[M].北京：北京计量出版，2006:10-18.

[3] 杨囡,王健,任孝平,等.自动无扰动系统的微克质量标准研究[J].中国计量学院学报,2015,26(2):172-176,187. YANG Nan, WANG Jian, REN Xiaoping, et al. Study on microgram mass standards based on automatic mass comparator[J]. Journal of China University of Metrology,2015,26(2):172-176,187.

[4] 沈昱明,张进明.对流量测量不确定度评估中若干名词术语的看法[J].计量学报,2016(1):109-112. SHEN Yuming, ZHANG Jinming. Perspective on some terminology of evaluation of flow measurement uncertainty[J]. Acta Metrologica Sinica,2016(1):109-112.

[5] 魏峰,狄蕊,陈钦保,等.酸碱滴定不确定度计算软件的研发[J].黄山学院学报,2010,12(3):43-45. WEI Feng, DI Rui, CHEN Qinbao, et al. Research and development of uncertainty calculation software for acid-base titration[J]. Journal of Huangshan University,2010,12(3):43-45.

[6] 赵化甜,荆学东,姜健,等.传感器测量不确定度评估方法的分析[J].煤炭技术,2015,34(6):219-221. ZHAO Huatian, JING Xuedong, JIANG Jian, et al. Evaluation of measurement uncertainties of transducer[J]. Coal Technology,2015,34(6):219-221.

[7] 姬中华,邱跃龙,程秀芹,等.基于蒙特卡洛法的铝合金抗拉强度测量不确定度评定[J].理化检验-物理分册,2015,51(6):434-437. JI Zhonghua, QIU Yuelong, CHENG Xiuqin, et al. Evaluation on measurement uncertainty of tensile strength of aluminium alloy based on monte carlo method[J]. Physical Testing and Chemical Analysis Part A:Physical Testing，2015,51(6):434-437.

[8] 熊朝晖,陈衷.温度试验箱校准的测量不确定度[J].计量与测试技术,2010(11):71-73. XIONG Chaohui, CHEN Zhong. Uncertainty of the calibration for temperature test chamber[J]. Metrology & measurement technique,2010(11):71-73.

[9] 杨图强.基于MATLAB的MCM对GUM不确定度框架验证[J].质量技术监督研究,2014(6):32-36. YANG Tuqiang. MCM for GUM uncertainty framework verification based on MATLAB[J]. Quality and Technical Supervision Research,2014(6):32-36.

[10] 潘俊,温秀兰.圆度误差评定与测量不确定度计算[J].南京工程学院学报(自然科学版),2015(1):1-5. PAN Jun, WEN Xiulan. Evaluation of circularity errors and computation of measurement uncertainty[J]. Journal of Nanjing Institute of Technology (Natural Science Edition)，2015(1):1-5.

[11] 刘智敏.分布传播及其在不确定度中的应用[J].中国计量学院学报,2008,19(1):1-9. LIU Zhimin. Propagation of distributions and its application on uncertainty[J]. Journal of China University of Metrology,2008,19(1):1-9.

Development of adaptive Monte Carlo method software for the evaluation of uncertainty measurement

CHEN Chaoyun, WANG Can, WEN Huiqing, WANG Lianjiong, JIN Yuan

(Shanghai Institute of Measurement and Testing Technology, Shanghai 201203, China)

The uncertainty evaluation of Monte Carlo method (MCM) measurement is complex with its large amount of calculation. The present software is usally used only in a certain model. The models are independent and the result of the evaluation lacks the adaptive process. On LabVIEW software, we designed the software for the adaptive MCM measurement of uncertainty. The pseudo random number inputXwas generated. The discrete sampling of the probability density function (PDF) ofXwas conducted to get the discrete sampling values of outputY. The software was used to self-define the general model of mathematical formula with strong self-adaption. The algorithm of adaptively increasing sample sizeMwas focused. The effectiveness of the software in the evaluation of the general model was verified with the JJF1059.2-2012 example.

adaptive MCM; uncertainty measurement; LabVIEW; software development

2096-2835(2016)04-0406-05

10.3969/j.issn.2096-2835.2016.04.009

2016-08-15 《中国计量大学学报》网址：zgjl.cbpt.cnki.net

TB933

A