基于BISHOP法的某水利工程滑坡稳定性计算研究及评价

2017-01-11徐镇南邓志华

水利规划与设计 2016年8期

关键词：抗滑桩滑坡体数学模型

徐镇南，邓志华

(江西赣禹工程建设有限公司，江西南昌 330038)

基于BISHOP法的某水利工程滑坡稳定性计算研究及评价

徐镇南，邓志华

(江西赣禹工程建设有限公司，江西南昌 330038)

文章在勘探江西省某水电站滑坡特征及详细评价该工程滑坡体稳定性的基础上，采用BⅠSHOP法结合微分分析工具及多元函数求极值的数学原理对江西省某水电站滑坡的危险性进行了计算，有效避免了浩繁的计算量和函数发散的风险，为水利工程建设决策提供了科学合理的依据。

BⅠSHOP法;拟牛顿法;广义数学模型

DO I:10.3969/j.issn.1672-2469.2016.08.026

1 工程概况

江西省某水电站装机容量为15kw，最大水头高度为10m，引用流量为150m3/s，无调节的堤坝，正常蓄水位为1665m，设计的坝高为7～10m，主要承担发电任务，隶属于Ⅳ等小(1)型。根据《地质灾害危险性评估技术要求》中有关建设重要性分类表可知，该工程项目的地质环境条件可以评估为复杂地区，工程评定为二级危害。

该水电站库区右岸为基岩滑坡群发育地，位于库尾至下坝轴线上游之间的610m范围内，滑坡体的厚度尺寸处于15～40m的范围中，滑坡滑动的纵向长度尺寸可达到100～250m范围，滑坡前缘沿河床方向的横向宽度尺寸大约为1.5km，同时最大和最小的坡高分别可达60m和15m。为了确保滑坡群的整体稳定性，采用科学运用积分数学模型计算方法来评估滑坡体的稳定性和危害性，以更好地为水电站建设决策提供必要的依据。

2 滑坡的特征及危险性评估

2.1 滑坡特征

水电站工程建设区位于水河流域部位，地下水主要集中在第四系基层裂隙和松散堆积层中，并以地表渗流和径流的方式排入到附近的湟水河中。该水电站所处地区的地震动峰值加速度和特征周期数值分别为0.15g和0.45s，其基本烈度为Ⅶ度，并且构造运动主要以间歇性和差异性的升降运动为主。产生的滑坡也主要是由于地震活动以及外应力等的影响所造成的。另外，该地区其他地质特征还包括群粉砂质泥岩、滑坡体下浮粉砂质泥岩、红色基岩。

2.2 滑坡体特征

该地区滑坡体的典型纵剖面如图1所示。

由图1可知，该地区滑坡中部发育的“V”形冲沟将滑坡体分成了两块。可以按照方位的不同而分成东、西两块。前缘沿着河流方向的宽度尺寸为232m，并且其自然斜坡的走向也与相应河流的方向保持一致，具体为NW 298°，但是该坡体的坡面不太平顺，有多处发育有鼓包和冲沟问题，地貌、地形结构也相对比较复杂，总体滑坡体的坡度角度数值为26～30°。

3 边坡稳定性的量化分析

根据滑坡体特性，采用广义积分数学模型的推演、半解析解及验证进行工程中边坡的稳定性计算及分析。

3.1 积分数学模型的推演

图2中，坡高为H;点O是坐标原点，坡脚在其右上方处，水平距离为1.5H，竖直距离为 H; O′是滑弧的圆心，R为滑弧的半径;α为坡角;区域D坡底、坡面和坡顶与滑弧所围城区域;黑色条带部分为土条;i是土条的编号;θi是第i号土条的底面中点的法线与铅垂线的夹角，若θi位于铅垂线的左边则为负;若θi位于铅垂线的右边则为正。

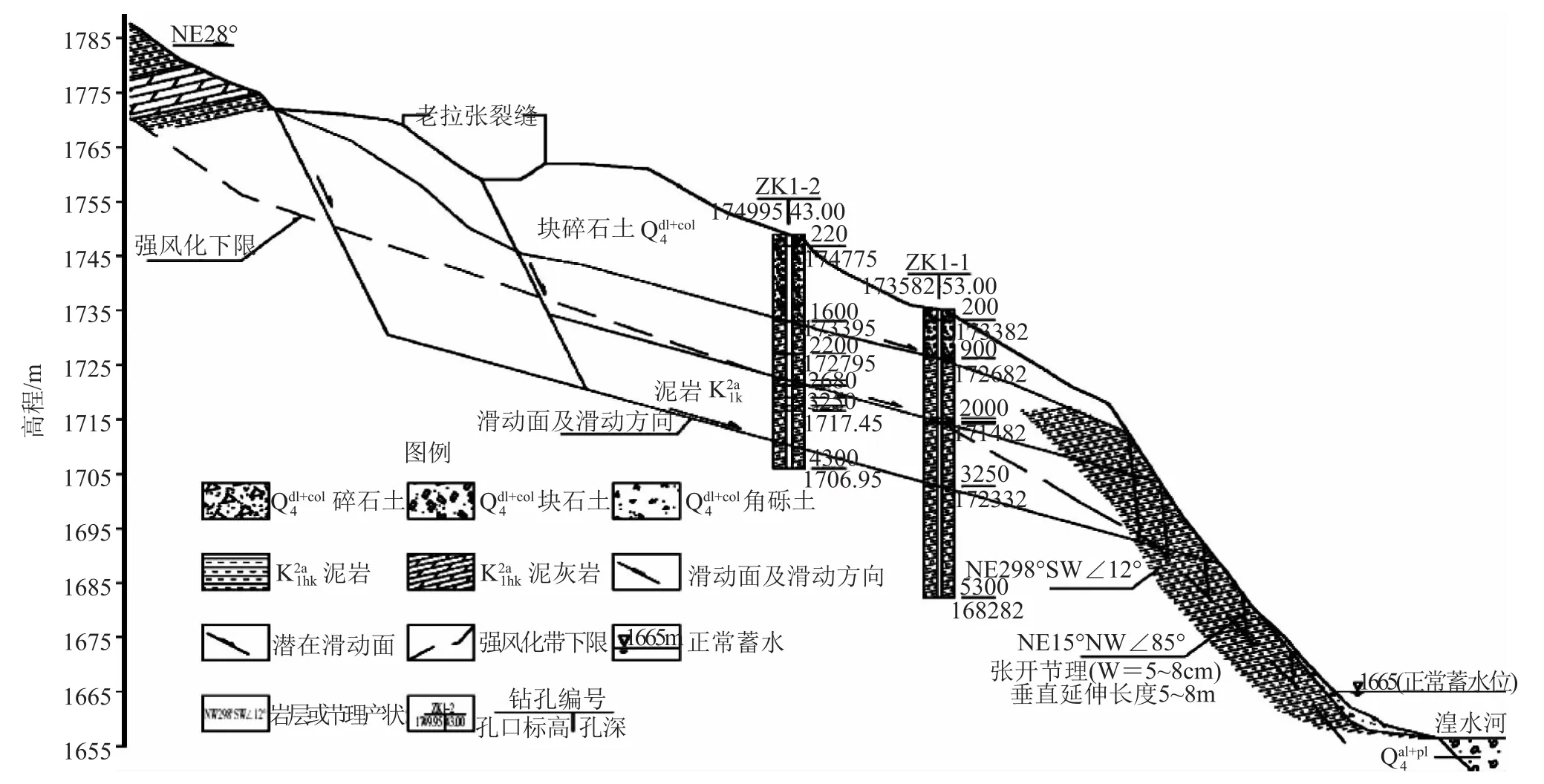
图1 滑坡体典型纵剖面

图2 坡体模型计算坐标系的建立

图3 土坡微分形式示意图

图3中，dσ为微分单元(为方便辨识，故意将图4中的微分单元dσ扩大)，θ是dσ的底面中点的法线与竖直线的夹角。图4中，滑弧的方程为:

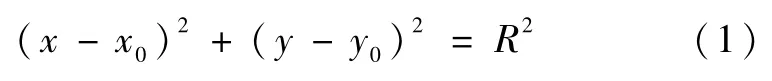
θ的正切即滑弧的斜率，数学表达为:

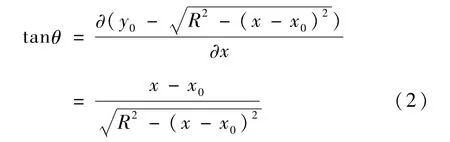
根据式2，得到θ的正弦和余弦，

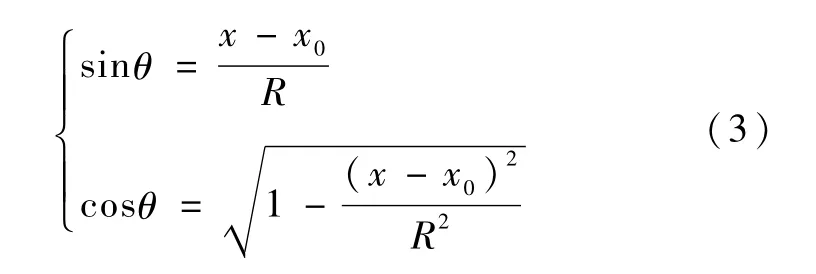
所以，微分单元

其中f(x)是坡底、坡面、坡顶的函数，对于一般规则边坡，

∑Wisinθi可写作:

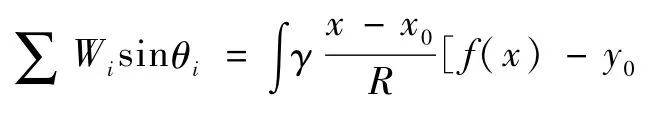
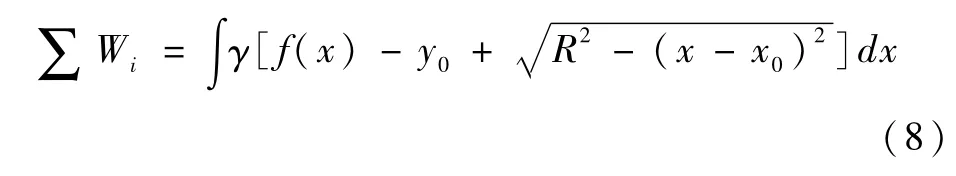
联立式4、5、6、7、8，得到BⅠSHOP法的积分形式:

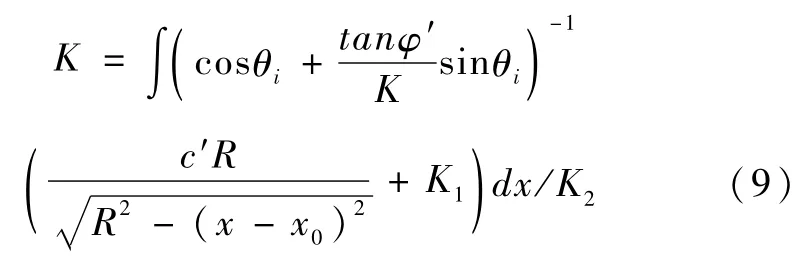
其中，

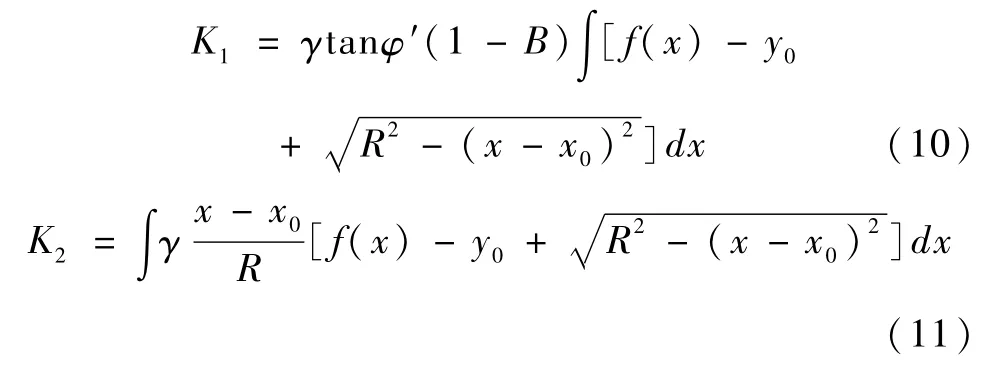
联立式9中等号右边的K提到等号的左边，写成如下形式:

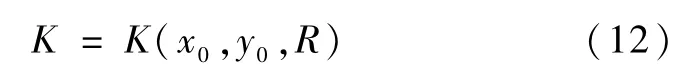
至此，建立了安全系数与滑弧位置的函数关系，K=K(x0，y0，R)。在此需要注意的是，安全系数K并非图1、图2、图3中x与y的函数。为便于理解，可设想一个四维空间，这个四维空间的元素为K、x0、y0、R，则K=K(x0，y0，R)是这个四维空间的三维流型。

根据三元函数取极值的公式，可以推导出其驻点恰好为极值点。因此，取极值的条件便为:

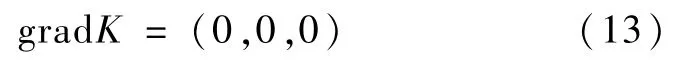
3.2 边坡稳定性计算断面的选择

先对各自断面进行计算，接着根据工程现场的测绘情况去分析计算中可能涉及的滑动剪出方式并对于滑体进行适当地分段编号处理，然后要计算出不同段号下的滑体边坡稳定性。

3.3 基于积分数学模型对边坡稳定性的解析

式13是超越方程，需用拟牛顿法求解它的实数解。

令

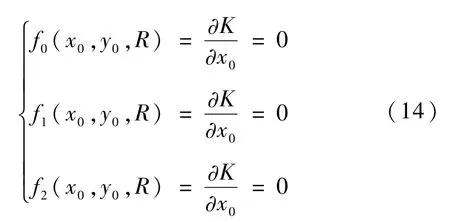
取X=(x0，y0，R)假设(x0，y0，R)第i次迭代的值为

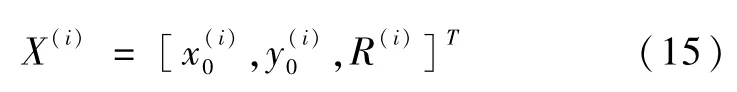
则第i+1次迭代的值为:

其中

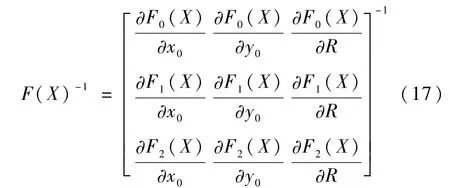
令

由此，我们给定一个精度ε和初值

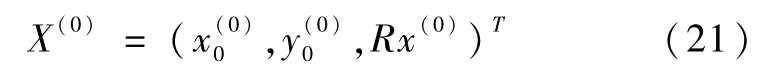
一直迭代，当

时便得结果。但是，得到的极值并不止一个，在所得极值之中，须选择满足K＞0、y0-R＜H、的那一个K(仅有一组)。

3.4 采用积分数学模型计算评价边坡的稳定性

通过对滑体整体变形情况以及钻孔岩芯等情况进行分析，该工程滑坡体滑动带计算指标为:粉砂质泥岩和松散堆积层的天然重度分别为21.0和20.0kN/m3，饱和中毒分别为21.5和20.5kN/m3;在天然工矿情况下，粉砂质泥岩和松散堆积层的抗剪强度分别为24.5kPa和25kPa。接着要合理划分该地的滑坡体，并分别按照天然工况和暴雨工况来计算其稳定系数。经过计算可知:1#滑坡体浅层滑动体在天然工况和暴雨工况下的稳定系数Ks分别为0.95和0.99;深层滑动体在二者工况下的稳定系数Ks分别为1.15和1.19。由于深层滑动稳定系数要比浅层滑动体的稳定系数大，所以该地区的滑坡主要表现为浅层滑动。

本工程的建筑等级为4级，相应的工程滑坡等级为5级，所以相应的稳定性评价需要根据5级边坡的分类标准来进行。根据《水利水电工程边坡设计规范》中有关稳定性评价的要求可以计算天然工程和暴雨工况下的浅层边坡稳定系数均小于1.10，所以滑坡处于失稳状态。

3.5 依照积分数学模型对边坡进行灾害预防处理

应对失稳情况，有效的处理办法是增设抗滑桩。分别取直径为0.2m的混凝土抗滑桩5、10、15、20、25个，沿坡面铺设，入土深度为1m，并利用积分数学模型进行计算，结果如下。

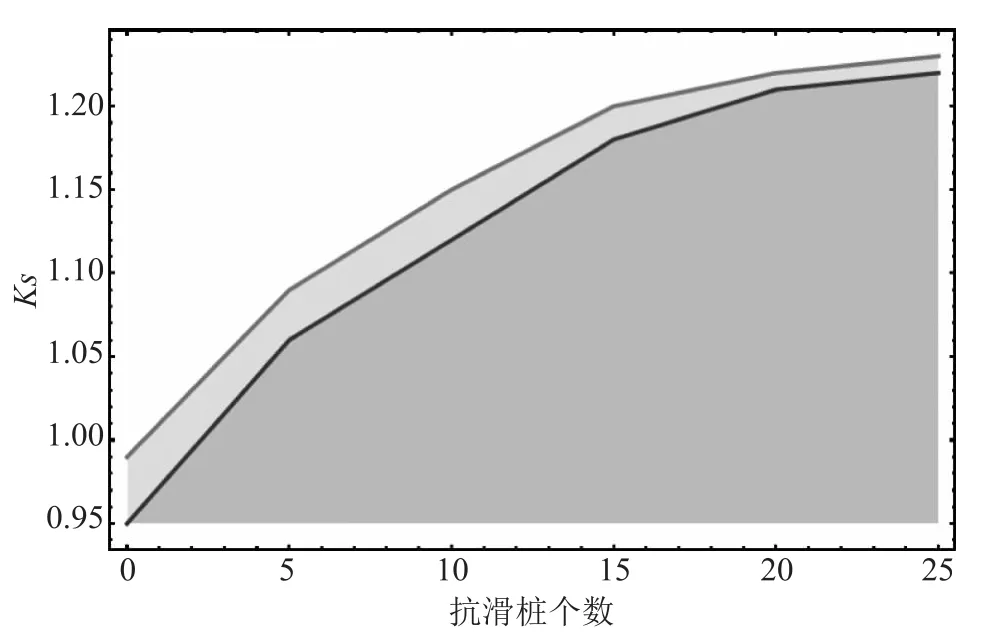
图4 抗滑桩个数与安全系数的关系

由上图可知，当铺设抗滑桩后，边坡的稳定性明显增加;随着抗滑桩的增多，边坡的稳定性也逐渐上升，增加的幅度却逐渐减小。但抗滑桩的个数大于15个，边坡的稳定性趋于1.2。考虑经济型的因素，选择抗滑桩10个，铺设深度为1m，其相应计算得到的稳定性级大于1.10，接着需要按照《水利水电工程边坡设计规范》规范中有关的要求来进行稳定性评价，滑坡处于稳定状态。

取直径为0.2m的混凝土抗滑桩10个，沿坡面铺设，入土深度分别为0.6m、0.8m、1m、1.2m、1.4m，并利用积分数学模型进行计算，结果如下。

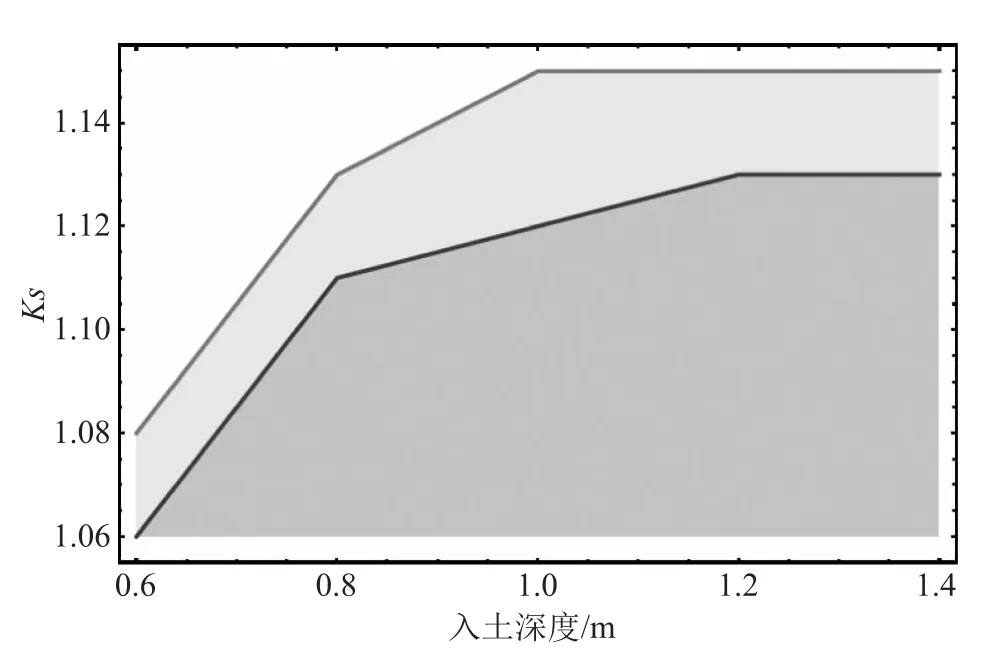
图5 入土深度与安全系数的关系

由上图可知，随着入土深度的增加，边坡的稳定性明显增加，边坡的稳定性也逐渐上升，增加的幅度却逐渐减小。抗滑桩的个数大于15个，边坡的稳定性趋于1.2。考虑经济型的因素，选择抗滑桩10个，铺设深度为0.8m，其稳定性级大于1.10，按 SL386-2007《水利水电工程边坡设计规范》进行稳定性评价，滑坡处于稳定状态。

4 结论

我国是世界上滑坡灾害比较的严重的国家之一，通过利用半解析BⅠSHOP法对边坡稳定性安全系数的计算得出了精确度最高的安全系数，基于此种计算结果不仅提出了江西省某水利工程中边坡的灾害预防处理措施，更对滑坡治理过程中的滑坡监测、分析、预报及稳定性评价具有非常重要的作用，完全满足滑坡治理预应力锚索设计的要求和目的。

［1］赵明阶，何光春，王多垠.边坡工程处治技术［M］.北京:人民交通出版社，2003.

［2］FELLENⅠUSW.Calculationofthestabilityofearthdams［J］.Trans2nd-CongLargeDams，1936(04):445.

［3］BⅠSHOPAW.Theuseoftheslipcircleinthestabilityanalysisofslopes［J］. Geotechnique，1955，5(01):7-17.

［4］JANBUN.Slopestabilitycomputations，embankmentdamengineering［M］.NewYork:JohnW ileyandSons，1973:47-86.

［5］SAMASK.Stabilityanalysisofembankmentsandslopes［J］.Geotechnique，1973，23(03):423-433.

［6］MORGERSTEMNR，PRⅠCEVE.Theanalysisofthestabilityofgeneralslipcircles［J］.Geotechnique，1965，15(01):79-93.

［7］SPENCERE.Amethodofanalysisofthestabilityofembankmentsusingparallelintersliceorces［J］.Geotechni-que，1967，17(01):11-22.

［8］朱大勇，邓建辉，台佳佳.简化Bishop法严格性的论证［J］.岩土工程学报，2007，26(03):455-458. ［9］陈祖煜.土坡稳定分析通用条分法及其改进［J］.岩土工程学报，1983，5(04):11-27.

［10］戴自航，沈蒲生.土坡稳定分析简化Bishop法的数值解［J］.岩土力学，2002，23(06):760-764.

［11］蒋斌松，康伟.边坡稳定性中BⅠSHOP法的解析计算［J］.中国矿业大学学报，2008，37(03):287-290.

［12］张鲁渝，郑颖人.简化Bishop法的扩展及其在非圆弧滑面中的应用［J］.岩土力学，2004(06).

［13］李亮，杨小礼，禇雪松，等.基于Bishop法假定的边坡临界滑动场方法及应用［J］.中南大学学报(自然科学版)，2011(09).