一类具有不同岛序列的连通图

赵小玲

(上海电机学院 数理教学部，上海 201306)

一类具有不同岛序列的连通图

赵小玲

(上海电机学院 数理教学部，上海 201306)

令G=(V，E)是一个简单图，图G的L(2,1)标号是一个映射f:V(G)→{0,1,…}，使得对任意的u,v∈V(G)，若dG(u,v)=1,则|f(u)-f(v)|≥2;若dG(u,v)=2,则|f(u)-f(v)|≥1。基于图G的L(2,1)标号与其补图GC的路覆盖之间存在着对应的关系，通过对补图的不同路覆盖的研究，得到了一类具有至少两个不同岛序列的特殊的连通图——M-圈串图的补图。

L(2,1)标号; 洞指数; 岛序列; 连通图

顶点的距离-2标号问题来源于Hale所介绍的频道分配问题，最早在文献[1]中进行了研究。假设给定一些无线电发射台，必须给每个电台分配一个频道且要避免频道之间相互干扰。用非负整数代表不同的频道，为减少干扰，任何两个“接近”的电台必须分配到不同的频道，任何两个“非常接近”的电台必须分配到距离至少为2的频道。为了解决该问题，可以构作这样的一个简单无向图G=(V，E)：顶点u和v之间的距离是u和v之间的最短路的长度，记作dG(u,v)。若两个顶点是“非常接近”的，则在图中它们是相邻的；若两个顶点是“接近”的，则它们在图中的距离为2。

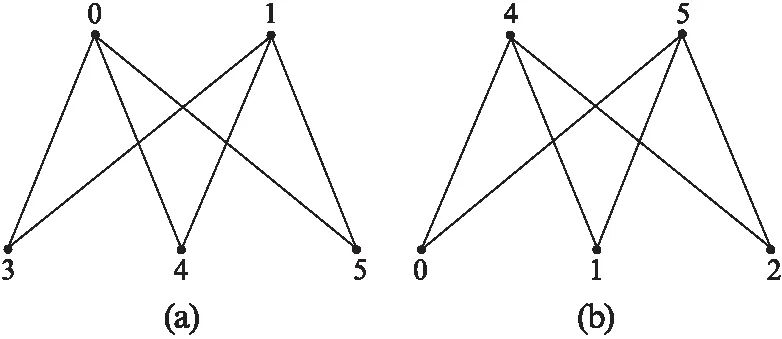
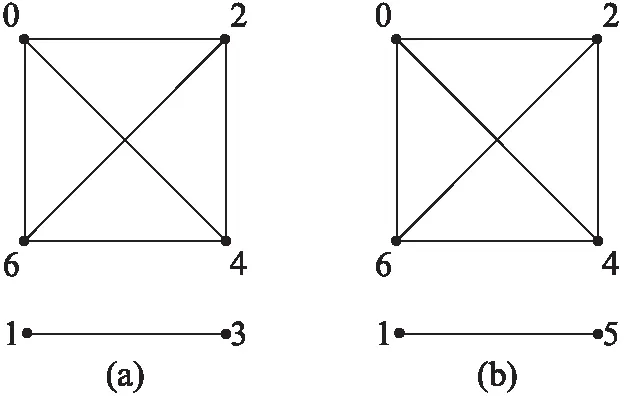
图G的L(2,1)标号是映射f:V(G)→{0,1,…}，使得对任意的u,v∈V(G)，若dG(u,v)=1,则|f(u)-f(v)|≥2;若dG(u,v)=2,则|f(u)-f(v)|≥1。图G的k-L(2,1)标号是图G的一个L(2,1)标号，使得所用到的标号最大为k；图G的L(2,1)标号数记作λ(G)，定义为[2]λ(G)=min{k|G有一个k-L(2,1)标号}。若图G的k-L(2,1)标号中标号h(0

由于在交叉学科和应用领域中的重要性，图G的L(2,1)标号问题得到了广泛研究。作为L(2,1)标号的一个重要特征，图G的岛序列也成为了一个主要的研究方向。文献[3-4]中对此作了很多研究。一些不连通图，由于它们的结构比较疏松，较容易得到它们的一些具有不同岛序列的λ(G)-L(2,1)标号。那么，对于结构比较紧密的连通图是否也有此结论？文献[3]中提出了一个公开问题：是否存在一些连通图至少具有2个λ标号的不同岛序列？

基于图G的L(2,1)标号与其补图GC的路覆盖之间存在着的对应关系，本文主要通过探讨其补图的不同的路覆盖，得到了一类至少有两个λ标号的不同岛序列的连通图：M-圈串图的补图。本文中未详细描述的术语和符号参见文献[5-6]，文中涉及的一些其他线索可参考文献[7-13]。

1 理论基础

有些图，它们不同的λ(G)标号有相同的岛序列，如图1中的完全二分图K2,3的两个不同的λ=5,ρ=1的标号，有相同的岛序列(2,3)；而有些图，它们不同的λ(G)标号对应有不同的岛序列，如图

2中的不连通图K4∪P2的2个不同的λ=6,ρ=1的标号，有不同的岛序列(5,1)和(3,3)。

图1 K2,3的2个λ-L(2,1)标号Fig.1 Two λ-L(2,1) labelings of K2,3

图2 K4∪P2的2个λ-L(2,1)标号Fig.2 Two λ-L(2,1) labelings of K4∪P2

那么，对于连通图，是否可能至少具有2个不同的λ标号的岛序列？本文考察M-圈串图G的路覆盖和它的补图GC的岛序列。

定义1G=(V,E)是一个简单图，图G的一个路覆盖是指G中包含了所有顶点的点不交路的集合。图G的具有最少路数的一个路覆盖中路的数目称为图G的路覆盖数，用P(G)表示。恰有P(G)条路的一个路覆盖称为图G的最小路覆盖。

定义2不包含相邻的且度数大于2的顶点对的图称为2-稀疏图。

定义3由M+1条长度大于1的路连接M个点不交的圈形成的图称为M-圈串图，如图3所示。显然M圈串图是一个有2个叶子的2-稀疏图。

图3 M-圈串图Fig.3 M-circles string

引理1[14]令G是一个有m≥1条边、n个顶点、l个叶子的2-稀疏图。若G不是圈图，则P(G)=l+m-n。

引理2[15]令G是一个有n个顶点的图，则λ(G)=n+P(GC)-2，当且仅当P(G)≥2。

引理3[3]令G是一个有n个顶点的图，若λ(G)≥n-1，则ρ(G)=P(GC)-1。

2 主要结论

定理1令G是一个M-圈串图，则GC是连通图。

证明设w1、w2是M-圈串图G的两个叶子，u和v是G中任意两个不同的顶点。

若u和v恰好是w1和w2，则由于w1、w2是M-圈串图的两个叶子，它们在G中不相邻，故w1、w2在GC相邻。此时w1w2(即uv)是GC中连通u和v的一条路。以下假设u和v均不是w1或w2。

情况1u和v在GC中相邻，则uv为GC中连通u和v的一条路。

情况2u和v在GC中不相邻。

(1)u和v在G中均不与wi(i=1,2)相邻，则u和v在GC中均与wi(i=1,2)相邻，此时，uw1v或uw2v都是GC中连通u和v的一条路。

(2)u和v中的一个在G中与wi(i=1,2)中的一个相邻，另一个在G中与wi(i=1,2)均不相邻。不失一般性，设u在G中与w1相邻，v在G中与wi(i=1,2)均不相邻。此时，u在GC中与

w2相邻，v在GC中也与w2相邻，因此，uw2v是GC中连通u和v的一条路。

(3)u和v中的一个在G中分别与wi(i=1,2)中的一个相邻。不失一般性，设u在G中与w1相邻，v在G中与w2相邻，则在GC中，u与w2相邻，v与w1相邻。又因为w1、w2是M-圈串图的两个叶子，它们在G中不相邻，故w1、w2在GC中相邻。此时，uw2w1v是GC中连通u和v的一条路。

综上所述，G中的任意两个不同的顶点u和v在GC中都是连通的，故GC是连通图。 证毕

定理2令G是一个M-圈串图，则GC至少有2个不同的λ标号的岛序列。

证明由定义3可知，若G是一个有n个顶点、m条边的M-圈串图，则m=n+M-1。由引理1，

P(G)=l+m-n=2+(n+M-1)-n=M+1

本文给出G的2个最小路覆盖以及对应的GC的岛序列。

(1) 如图4所示，令P1=u11u12…u1n1；P2=u21u22…u2n2；…；PM=uM1uM2…uMnM；PM+1=u(M+1)1u(M+1)2…u(M+1)nM+1。

图4 M-圈串图的一个路覆盖Fig.4 A path covering of M-circles string

对应此最小路覆盖，得到如下GC的L(2,1)标号：

f(u1i)=i-1, i=1,2,…,n1

f(u2i)=n1+i, i=1,2,…,n2

⋮

f(uMi) =n1+n2+…+nM-1+ i+M-2, i=1,2,…,nM

f(u(M+1)i)=n1+n2+…+nM+i+ M-1, i=1,2,…,nM+1

此时，标号f的标号数为

n1+n2+…+nM+nM+1+M-1=

n+M-1=n+(M+1)-2= n+P(G)-2

由引理2，有

n+P(G)-2=λ(GC)

故标号f为GC的一个λ-L(2,1)标号。

又由引理3，有

ρ(GC)=P(G)-1=M+1-1=M

可得到GC的一个有M个洞的λ标号的岛序列(n1,n2,…,nM,nM+1)。

对应此最小路覆盖，得到GC的L(2,1)标号：

图5 M-圈串图的另一个路覆盖Fig.5 Another path covering of M-circles string

此时标号f′的标号数为

l1+l2+…+lM+lM+1+M-1=n+M-1=n+(M+1)-2=n+P(G)-2

由引理2，有

n+P(G)-2=λ(GC)

故标号f′也是GC的一个λ-L(2,1)标号。

又由引理3，有

ρ(GC)=P(G)-1=M+1-1=M

可得到GC的一个有M个洞的λ标号的岛序列(l1,l2,…,lM,lM+1)。

因此，M-圈串图的补图是一类具有不同岛序列的连通图。

证毕

[1] GRIGGS J R，YEH R K.Labelling graphs with a condition at distance 2[J].SIAM Journal on Discrete Mathematics,1992,5(4):586-595.

[2] CHANG G J,KUO D.TheL(2,1)-Labeling problem on graphs[J].SIAM Journal on Discrete Mathematics,1996,9(2):309-316.

[3] GEORGES J P,MAURO D W. On the structure of graphs with non-surjectiveL(2,1)-labelings[J].SIAM Journal on Discrete Mathematics,2005,19(1):208-223.

[4] GEORGES J P,MAURO D W.A note on collections of graphs with non-surjectiveL(2,1)-labelings[J].Discrete Applied Mathematics,2005,146(1):92-98.

[5] WEST D B.Introduction to Graph Theory[M].2nd ed.Upper Saddle River,NJ.Prentice Hall,Inc,2001.

[6] BONDY J A，MURTY U S R.Graph theory with applications[M].London:The Macmillan Press,Ltd,1976.

[7] FISHBURN P C,ROBERTS F S.No-holeL(2,1)-coloring[J].Discrete Applied Mathematics,2003,130(3):513-519.

[8] CHANG G J,LU Changhong.Distance-two labelings of graphs[J].European Journal of Combinatorics, 2003,24 (1):53-58.

[9] SHAO Zhendong, LIU Jiazhuang.TheL(2,1)-labeling problem on several classes of graphs[J].Mathematica Applicata,2004,17(1)：31-36.

[10] GEORGES J P,MAURO D W.On the structure of graphs with non-surjectiveL(2,1)-labelings[J].SIAM Journal on Discrete Mathematics,2005,19(1):208-223.

[11] YEH R K.A survey on labeling graphs with a condition at distance two[J].Discrete Mathematics,2006,306(12):1217-1231.

[12] LU Changhong,CHEN Lei, ZHAI Mingqing.Extremal problems on consecutiveL(2,1)-labellings[J].Discrete Applied Mathematics,2007,155(10):1302-1313.

[13] LU Changhong,ZHAI Mingqing.An extremal problem on non-full colorable graphs[J].Discrele Applied Mathematics,2007,155(16):2165-2173.

[14] ADAMS S S,TRAZKOVICH A,TROXELL D S,et al.On island sequences of labelings with a condition at distance two[J].Discrete Applied Mathematics,2010,158(1):1-7.

[15] GEORGES J P,MAURO D W,WHITTLESEY M A.Relating path covering to vertex labelings with a condition at distance two[J].SIAM Journal on Discrete Mathematics,1994,135(1/3):103-111.

A Class of Connected Graphs with Multiple Island Sequence

ZHAO Xiaoling

(Department of Mathematics and Physics, Shanghai Dianji University, Shanghai 201306, China)

LetG=(V，E) be a simple graph. TheL(2,1)-labeling ofGis a functionf:V(G)→{0,1,…} such that anyu,v∈V(G),|f(u)-f(v)|≥2 ifdG(u,v)=1, and |f(u)-f(v)|≥1 if,dG(u,v)=2.Based on the relation between theL(2,1)-labeling ofGand the path covering ofGC, we observe different path covering of the complement ofGand reach a class of connected graphs with multiple island sequence —the complement ofM-circles string.

L(2,1)-labeling; hole index; island sequence; connected graph

2016-05-16

赵小玲(1970-)，女，副教授，主要研究方向为图论及其应用，E-mail:zhaoxl@sdju.edu.cn

2095-0020(2016)06-0369-04

O 157.5

A