无界区域上抛物型外问题的Schwarz交替算法

鞠 银

(上海电机学院 数理教学部, 上海 201306)

无界区域上抛物型外问题的Schwarz交替算法

鞠 银

(上海电机学院 数理教学部, 上海 201306)

主要研究无界外区域上抛物型方程。由自然边界归化理论得到了自然积分算子K的具体表达式，并利用Schwarz交替算法给出重叠区域的区域分解格式，最后给出收敛性分析。

无界区域; 抛物方程; 外问题; Schwarz交替算法; 区域分解

科学与工程计算中经常遇到依赖时间的无界区域问题[1-11]，故求解此类无界区域问题变得十分重要。由于涉及到时间变量，有研究者先对时间离散，得到半离散化问题，然后获得人工边界条件，利用有限差分或有限元方法来求解[1]；有研究者利用构造法获得依赖时间的无界外问题的精确和近似的人工边界条件[2]。本文主要研究无界外区域上抛物型方程，由自然边界归化理论[12]得到了自然积分算子K的具体表达式，并利用Schwarz交替算法[13]给出了重叠区域的区域分解格式，最后对收敛性进行分析。

1 对时间离散化

设Ω为中心在原点半径为R的圆周Γ的外部，即

Γ={(x，y)}|x2+y2=R2

对任意固定的正实数T，记J∶=(0，T)。考虑如下初边值问题:

(1)

(2)

u(χ，0)=u0(χ)，χ∈Ω

(3)

式中，χ=(x，y)；Δ为Laplace算子，即

函数f(χ，t)、g(χ，t)、u0(χ)均为满足适当条件的已知函数；∂u/∂t为未知函数u(χ，t)关于时间的导数；∂u/∂n为沿边界Γ的法向导数。假设函数u(χ，t) 在无穷远处有界。

(1) 由自然边界元法的理论可知，其主要任务就是寻找自然积分算子K的具体表达式及实现其数值求解。先将式(1)对时间进行离散化，设τ为时间步长，并记tk=k·τ，第k层的值uk(x)=u(x，tk)，其中，k=1，2，…，[T/τ]；令zk(x)=ut(x，tk)，有

zk-Δuk=fk

(4)

(5)

式中，γ∈(0，1]。

由式(4)、(5)得

(1-γτΔ)uk=uk-1+τ(1-γ)zk-1

(6)

(7)

当γ=1时，有

zk=(uk-uk-1)/τ

对每个k，式(6)为椭圆型方程，即Helmholtz方程。

(2) 预估值为

(8)

(9)

(10)

(11)

(3) 校正过程

(12)

Δuk-λ2uk=λ2fk

(13)

由自然边界归化理论，在极坐标系里，可得

uk(r，θ)=

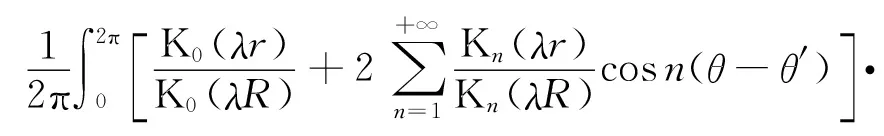
uk(R，θ′)dθ′+F(λ，R，fk，r，θ)

(14)

N(λ，R，fk，θ)

(15)

式中，r、θ分别为极径和极角；Kn为第二类修正的柱贝塞尔函数；

F(λ，R，fk，r，θ)=

(16)

(17)

式中，

(18)

(19)

(20)

2 重叠区域的Schwarz交替算法及其几何收敛性

在Ω内取两个同心圆：

其中，R1>R2>R。区域Ω被分成两个重叠的子区域：有界区域Ω1(由R和R1围成的环形区域)和无界区域Ω2(以R2为内边界的外区域)，Ω1∩Ω2≠∅，记

给出Schwarz交替算法[4]:

(21)

(22)

Vk={v|v∈H1(Ω1)}

(23)

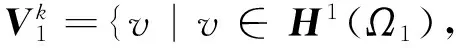
(24)

(25)

(26)

(27)

式中，

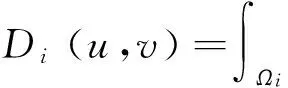
所以说，当我们有着快乐的情绪时，学生就会容易接纳我们，他们就会很愿意积极的参与到课堂当中来，喜欢积极的探究问题，提高兴趣，增强注意力。

(28)

(29)

(30)

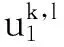
于是有

(31)

因此，式(21)、(22)的变分形式如下：

(32)

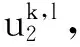
(33)

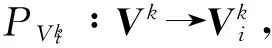
(34)

(35)

由此可得

(36)

(37)

(38)

(39)

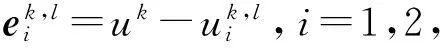
(41)

于是有

(42)

(43)

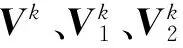
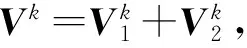
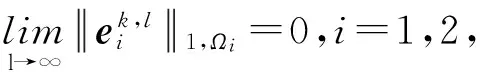
且有

定理1表明上述交替算法是几何收敛的。

3 收敛速度分析

(44)

由分离变量法得到

其中，I(z)为第一类变型贝塞尔函数。由

则得

(45)

求解方程式(45)，得

其中，Cn=cn(R2)；Dn=dn；

W0，n(2x)为惠泰克函数[14]。

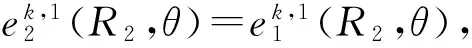
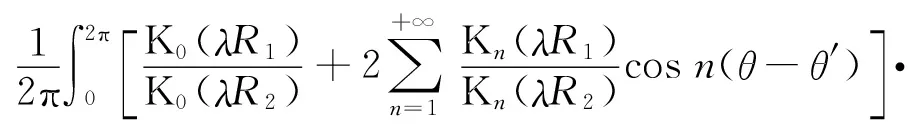
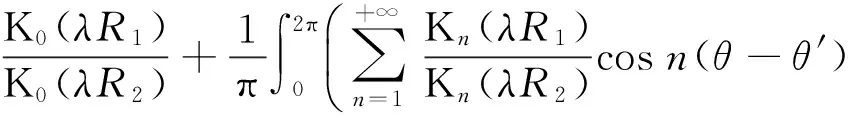
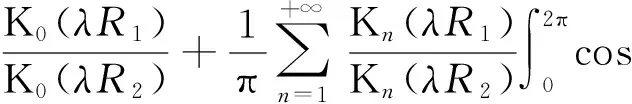
其中，C为常数。

类似地，可得

故由数学归纳法，可得以下定理。

定理2设Γ是以原点为圆心，半径为R的圆，Γ1和Γ2是与Γ同心且半径分别为R1和R2的圆，R1>R2>R。在每个时间层上，利用Schwarz交替算法式(21)、(22)求解式(1)～(3)，则有

最后由迹定理可得

因此，R2/R1的值越小，即2个区域重叠程度越高，收敛速度越快。

[1] 艾焰，杜其奎，冯崇岭.凹角区域双曲外问题的精确人工边界条件[J].高校应用数学学报，2007，22(4)：447-454.

[2] 杜其奎，余德浩.抛物型初边值问题的自然积分方程及其数值解法[J].计算数学，1999，21(4)：495-506.

[3] 冯丹，杜其奎.椭圆外区域各向异性问题基于人工边界条件的Schwarz交替算法[J].高校应用数学学报，2011，26(2)：158-168.

[4] DU Qikui，YU Dehao.Domain decomposition methods based on natural boundary reduction for wave equation[J].Chinese Journal of Computation Physics，2001，18(5)：417-422.

[5] DU Qikui，TANG Minxia.Exact and approximate artificial boundary conditions for the hyperbolic problems in unbounded domains[J].Applied Mathematics and Computation，2005，169(1):544-562.

[6] HAN Houde，ZHENG Chunxiong.Exact nonreflecting boundary conditions for exterior problems of the hyperbolic equation[J].Chinese Journal of Computational Physics，2005，22(2):95-107.

[7] HAN Houde，HUANG Zhongyi.Exact and appro-ximating boundary conditions for the parabolic pro-blems on unbounded domains[J].Computers & Mathematics with Applications，2002，44(5/6):655-666.

[8] HAN Houde，HUANG Zhongyi.A class of artificial boundary conditions for heat equation in unbounded domains[J].Computers and Mathematics with Applications，2002，43(6-7):889-900.

[9] DU Qikui，YU Dehao.A domain decomposition methods based on natural boundary reduction for nonlinear time-dependent exterior wave problems[J].Computing，2002，68(2):119-129.

[10] DU Qikui，YU Dehao.Dirichlet-Neumann alternating algorithm based on the natural boundary reduction for time-dependent problems over an unbounded domain[J].Applied Numerical Mathematics，2003，44(4):471-486.

[11] GROTE M J，KELLER J B.Exact nonreflecting boundary conditions for the time dependent wave equations[J].SIAM Journal on Applied Mathematics，1995，55(2):280-297.

[12] 余德浩.自然边界元方法的数学理论[M].北京：科学出版社，1993.

[13] 吕涛，石济民，林振宝.区域分解算法——偏微分方程数值解新技术[M].北京：科学出版社，1992：269-299.

[14] 刘式适，刘式达.特殊函数[M].北京:气象出版社，1988:296.

A Schwarz Alternating Method for Parabolic Problem ina Unbounded Exterior Domain

JU Yin

(Department of Mathematics and Physics, Shanghai Dianji University, Shanghai 201306, China)

In this paper, we investigate the parabolic equation in an unbounded exterior domain. Using the principle of the natural boundary reduction, we obtain a specific expression of the natural integral operator K. We then use the Schwarz alternating algorithm to give a domain decomposition scheme and convergence analysis of the overlapping region.

unbounded domain; parabolic problem; exterior problem; Schwarz alternating algorithm; domain decomposition method

2015-12-09

鞠 银(1979-)，女，副教授，主要研究方向为计算数学，E-mail:juyin@sdju.edu.cn

2095-0020(2016)06-0359-05

O 241

A