基于非周期性维修的二维延伸保证策略研究

徐德凯

(天津大学 管理与经济学部，天津 300072)

基于非周期性维修的二维延伸保证策略研究

徐德凯

(天津大学 管理与经济学部，天津 300072)

采用基于可靠性的非周期性预防性维修策略，构建二维延伸性产品保证成本模型，并进行产品保证成本优化。通过算例验证了模型的有效性，并利用敏感性分析对影响模型结果的参数进行了评估。结论表明，在保证期边界参数确定的条件下，该策略可以降低二维延伸性产品保证成本。

二维产品保证；非周期预防性维修；延伸性产品保证

对于汽车制造商而言，在满足消费者延伸性服务需求的前提下，设计一套科学合理的二维延伸性汽车产品保证服务策略来降低制造商的延伸性产品保证成本显得至关重要。预防性维修经常被看作是提高产品可靠性、增加产品寿命的一种有效手段。回顾国内外近20年的文献，可以将包含保证和预防性维修的文献做以下分类：根据产品保证的维度划分为一维保证和二维保证；根据保证期的长短划分为基础保证和延伸性保证。国内外学者早期的研究多集中在一维保证[1-7]。

然而对于汽车这样的产品，仅考虑时间这一个维度是不够的，因为汽车是随着时间和使用程度而不断老化的，这两者都对产品的可靠性有影响。因此在实际中，采用考虑了时间和使用程度的二维产品保证更加合理。近几年来已经开始有学者对包含预防性维修的二维产品保证进行研究。SHAHANAGHI等[8]从时间和使用程度两个维度对具有延伸性保证的产品建立了失效模型、预防性维修效果模型及相应的保证成本模型，进而建立了相应的优化模型，得到了最优的PM维修次数和每次的维修程度；还为供应商提供了柔性的延伸性保证合同及相应的最优维修策略。HUSNIAH等[9]将服务策略延伸到二维产品保证，得到了相应的保证成本模型，结果表明与不包含预防性维修的服务策略相比，这种服务策略更优，保证成本更低。HUANG等[10]提出了基于可靠性的非周期性预防性维修策略，并建立了相应的保证成本模型，得到了最优的保证区域。HUANG等[11]从制造商的角度出发，采用二元失效分布法建立了基础保证期内考虑周期性预防性维修的二维产品保证成本模型，在预防性维修间隔和预防性维修程度确定的条件下得到了最优的基础保证政策。

从文献回顾可以看出，大部分都集中在一维产品保证的研究，对包含预防性维修的二维延伸性保证的研究尚不充分。此外，对包含预防性维修的产品保证研究多采用周期性的预防性维修策略，非周期性预防性维修的研究尚不多见[12-13]，但是文献[10]指出即使进行周期性的预防性维修，产品发生故障的频率也会越来越高，周期性的预防性维修并不是最优的服务策略。基于此，笔者采用基于可靠性的非周期性预防性维修策略对保证成本进行优化。

1 模型假设

(1)产品是广义的可修产品，失效率在整个保证范围内随着时间及使用程度递增。

(2)产品使用率随着消费者的不同而改变，但是同一消费者的使用习惯不变，即产品使用率在产品使用周期中是常数。

(3)基础保证期和延伸保证期内出现的故障，均采用最小性维修，且维修时间忽略不计。

2 二维延伸性产品保证数学模型

2.1 二维延伸性产品保证故障模型

在二维产品保证期内构建产品故障模型主要有3种方法：二元失效分布法、复合标度法[14]和边际方法。边际方法实际上是基于使用率的方法，其应用最多[15]，笔者也采用该方法。该方法假设对于一个特定的消费者来说，产品使用率在产品使用周期中是常数，但产品使用率Z随着消费者的不同而改变。因此Z是离散变量或概率密度函数为g(z)的连续变量。行驶里程u、时间t和产品使用率Z之间的关系为：

u(t)=Zt

(1)

对于一个特定的产品使用率Z=z，汽车首次失效的风险函数用h(t|z)表示，即失效率是使用时间和产品使用率的函数。ISKANDAR等[16]指出产品的失效是产品使用时间、使用程度、使用率等因素共同作用的结果，并提出了如下失效率函数:

h(t|z)=θ0+θ1z+θ2t+θ3u(t)

(2)

参数θ0，θ1,θ2,θ3可以根据历史维修数据、保证索赔数据通过多元线性回归的方法估计求得。根据式(1)可以将式(2)简化为：

h(t|z)=θ0+θ1z+(θ2+θ3z)t

(3)

2.2 二维延伸性产品保证策略描述

假设基础保证期和延伸保证期内产品出现故障均采用免费的最小性维修，且维修时间忽略不计，因此每个预防性维修区间内的失效可以定义为一个非均匀泊松过程，且强度函数λ(t|z)=h(t|z)。当汽车的可靠性降低到某个预先设定的值R时，就对汽车进行预防性维修，这意味着在每一个预防性维修区间的末端产品的可靠性都等于R。由产品可靠性和失效率的关系可得：

(4)

vi=vi-1+δ(m)(Ti-Ti-1)

(5)

式中：vi为第i次预防性维修后部件的虚拟寿命；Ti为第i次预防性维修的时间；m为预防性维修的程度(0≤m≤M)；m=0表示没有进行预防性维修，此时δ(0)=1；m=M表示完美预防性维修，此时δ(M)=0；δ(m)为虚拟寿命削减因子，是预防性维修程度m的函数。

δ(m)=(1+m)e-m

(6)

对于特定时间t，部件的虚拟寿命v(t)=vi-1+t-Ti-1，其中Ti-1≤t≤Ti。因为v0=0,T0=0，由式(5)可得：

v(t)=t-[1-δ(m)]Ti-1

(7)λi(t|z)=hi(v(t)|z)=θ0+θ1z+(θ2+θ3z)v(t)

(8)

由式(4)可得非周期预防性维修的时间安排为：

(9)

2.3 二维延伸性产品保证成本模型

2.3.1 Z=z条件下的二维延伸保证成本

当部件发生故障时采用最小性维修，延伸保证期间修正性维修的成本可表示为:

(10)

式中：K为延伸保证期间所进行的预防性维修的次数；τ1为基础保证的实际结束时间；τ2为延伸保证的实际结束时间。K，τ1，τ2的表达式分别为：K=argmax {Ti≤τ2|i∈N+}-argmin {τ1≤Ti|i∈N+},τ1=min {WB,UB/z}，τ2=min {WE,UE/z}。其中argmax {Ti≤τ2|i∈N+}表示满足Ti≤τ2的最大的i，argmin {τ1≤Ti|i∈N+}表示满足τ1≤Ti的最小的i。

延伸保证期间预防性维修所花费的成本为：

ECpm=cpmK

(11)

产品使用率Z=z的条件下，制造商在延伸保证期间所承担的总的保证成本为：

EC(Ω|z)=ECr+ECpm

(12)

2.3.2 无使用率约束条件下的延伸保证成本

(13)

2.4 二维延伸保证成本优化

假设R0为制造商根据市场竞争和对自身产品定位所设定的能够接受的最低可靠性，则二维延伸保证成本优化问题可看作为如下规划问题:

min EC(Ω)

(14)

s.t. TK≤τ2

(15)

0≤R0≤R≤1

(16)

式(15)表示最后一次预防性维修不能超过延伸保证的实际结束时间；式(16)表示产品可靠性不得低于制造商所能接受的最低可靠性水平。

3 数值计算

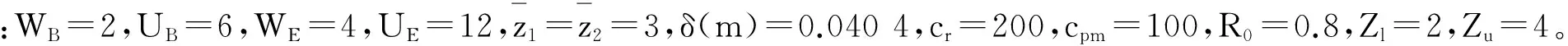
不同可靠性水平下的延伸性保证成本如表1所示。从表1可以看出，二维延伸保证成本随着可靠性的提高而不断增加，即二维延伸保证成本是可靠性的增函数。制造商设定的可靠性水平越高，则承担的二维延伸保证成本也越高。因此，制造商最优的决策是将可靠性边界参数设置为可以接受的最低可靠性水平，即R=R0。

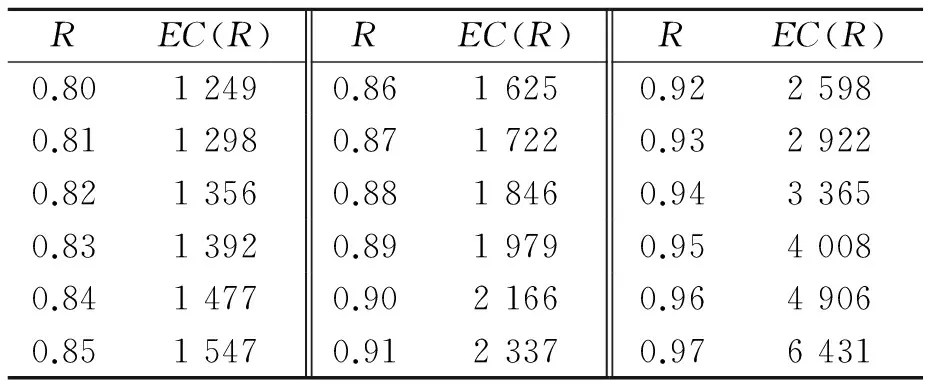
表1 不同可靠性水平下的延伸性保证成本

二维延伸性汽车产品保证策略如表2所示，其中Cpm(R*,K)为基于可靠性的非周期性预防性维修下的二维延伸性产品保证成本；Cpm(K)为周期性预防性维修下的二维延伸性产品保证成本；Cm为只采用最小性维修下的二维延伸性产品保证成本。从表2可以看出，随着产品使用率的增加，二维延伸性保证成本先逐渐增加又缓慢减少，在使用率等于平均使用率时达到最大值。这是因为随着产品使用率的增加，实际的产品保证期在逐渐缩短。此外，在制造商采用最优策略的前提下，对于不同使用率的消费者，采用笔者所提出的基于可靠性的非周期性预防性维修策略与采用周期性预防性维修策略和只采用最小性维修的维修策略相比，保证成本更低，从而验证了模型的有效性。

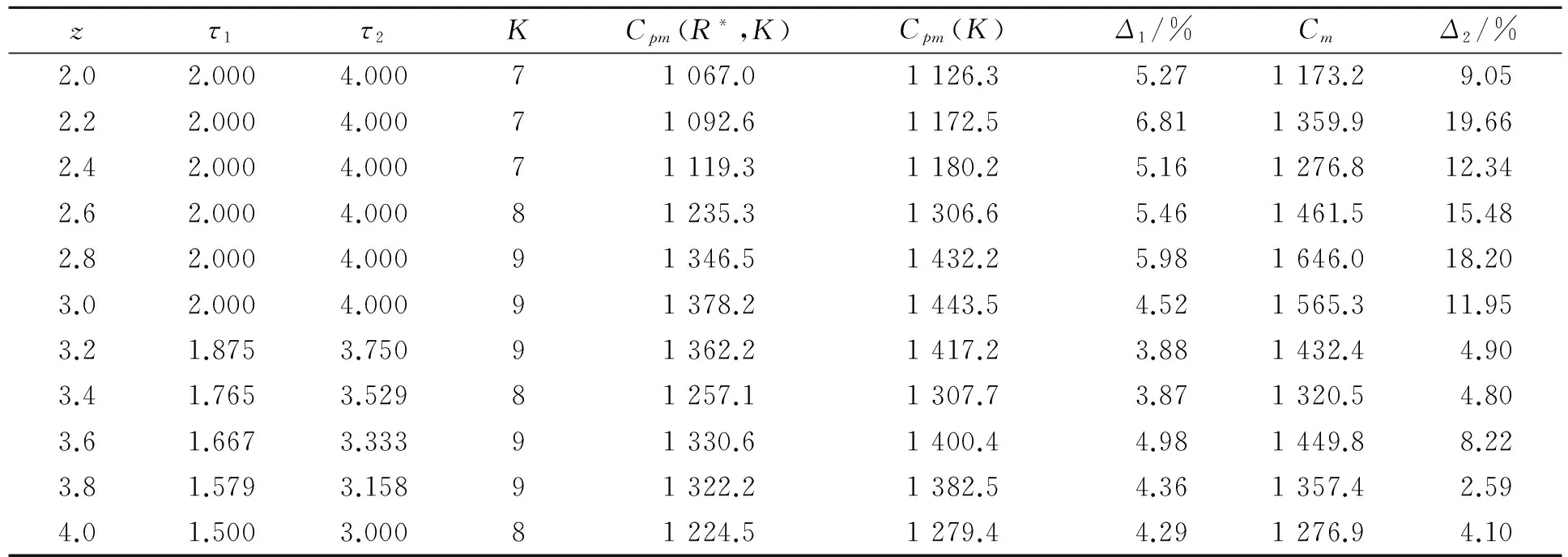
表2 二维延伸性汽车产品保证策略

Cr和Cpm的比值对保证成本优化效果的影响如表3所示，可以看出随着Cr和Cpm比值的增加，保证成本降低的百分比在不断增加。这意味着当预防性维修的成本相对于最小性维修的成本越小时，笔者所采用策略的优化效果就越明显。值得注意的是，当Cr/Cpm≤1.69时，Δ2为负值，这意味着预防性维修相对于最小性维修来说并不总是最优的维修策略。只有当Cr和Cpm之间满足一定的关系时，汽车制造商才可以通过采用预防性维修的策略来降低延伸性产品保证成本。

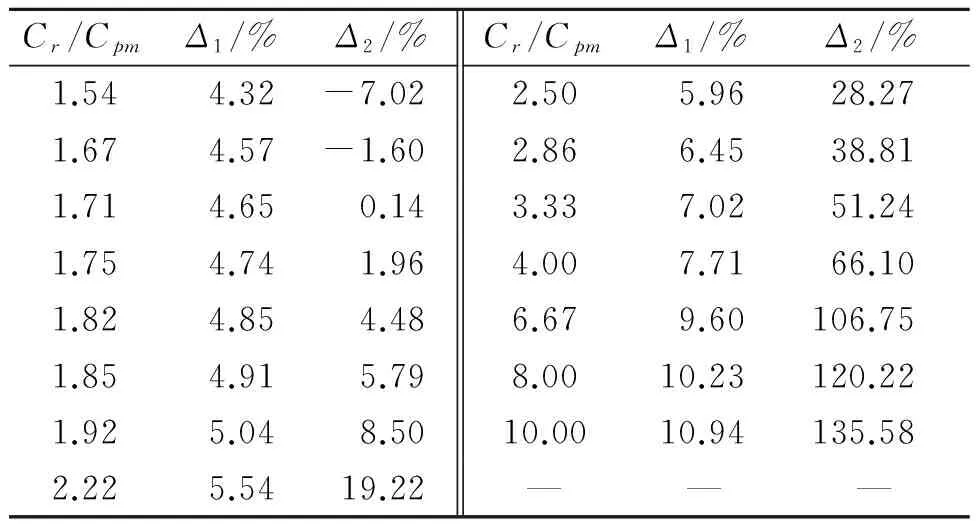
表3 Cr和Cpm的比值对保证成本优化效果的影响

4 结论

通过总结近年来国内外关于延伸性产品保证策略研究成果，进行了基于可靠性的非周期性预防性维修的二维延伸性产品保证策略研究。结果表明，笔者采用的维修策略比采用周期性预防性维修策略下的二维延伸性产品保证成本更低；但与只采用最小性维修的策略相比，预防性维修的策略并不总是最优的。笔者研究中还存在以下不足：①研究过程中把每次预防性维修的程度和成本设置成常数，以后的研究可以把每次预防性维修的程度看作一个变量，把每次预防性维修的成本看作是维修程度的函数，维修程度越大，相应的成本也越大。②笔者以汽车制造商延伸性保证成本最小化为目标，事实上成本最小化并不能保证制造商利润最大化，保证政策和维修策略都会对产品的销量产生影响。因此，以汽车制造商利润最大化为目标，考虑产品保证弹性的研究是未来需要进一步研究的内容。

[1] CHUN Y H.Optimal number of periodic preventive maintenance operations under warranty[J].Reliability Engineering & System Safety, 1992,37(3):223-225.

[2] JACK N,DAGPUNAR J.An optimal imperfect maintenance policy over a warranty period[J].Microelectronics Reliability, 1994,34(3):529-534.

[3] SAHIN I,POLATOGLU H.Maintenance strategies following the expiration of warranty[J].IEEE Transactions on Reliability, 1996,45(2):220-228.

[4] DJAMALUDIN I, MURTHY D N P,KIM C S.Warranty and preventive maintenance[J].International Journal of Reliability Quality & Safety Engineering, 2001，8(2):89-107.

[5] KIM C S, DJAMALUDIN I,MURTHY D N P.Warranty and discrete preventive maintenance[J]. Reliability Engineering & System Safety, 2004,84(3):301-309.

[6] PASCUAL R,ORTEGA J H.Optimal replacement and overhaul decisions with imperfect maintenance and warranty contracts[J].Reliability Engineering & System Safety, 2006，91(2):241-248.

[7] CHANG W L,LIN J H.Optimal maintenance policy and length of extended warranty within the life cycle of products[J].Computers & Mathematics with Applications, 2012，63(1):144-150.

[8] SHAHANAGHI K, NOOROSSANA R, JALALI-NAINI S G, et al.Failure modeling and optimizing preventive maintenance strategy during two-dimensional extended warranty contracts[J].Engineering Failure Analysis, 2013(28):90-102.

[9] HUSNIAH H, PASARIBU U S,ISKANDAR B P. A servicing strategy involving imperfect repair for two-dimensional warranties[C]∥2013 3rd International Conference on Instrumentation Control and Automation (ICA).[S.l.]:IEEE,2013:280-285.

[10] HUANG Y S, CHEN E,HO J W. Two-dimensional warranty with reliability-based preventive maintenance[J]. IEEE Transactions on Reliability, 2013，62(4):898-907.

[11] HUANG Y S, GAU W Y,HO J W. Cost analysis of two-dimensional warranty for products with periodic preventive maintenance[J]. Reliability Engineering & System Safety, 2015，134(2):51-58.

[12] CHANG W L, LIN J H. Optimal maintenance policy and length of extended warranty within the life cycle of products[J]. Computers & Mathematics with Applications, 2012,63(1):144-150.

[13] WANG Z, HUANG H Z, DU X. Optimal design accounting for reliability, maintenance, and warranty[J]. Journal of Mechanical Design, 2010,132(1):11007-11014.

[14] BLISCHKE W R, KARIM M R,MURTHY D N P. Warranty data collection and analysis[M].[S.l.]: Springer Science & Business Media,2011:205-234.

[15] JACK N, ISKANDAR B P,MURTHY D N P. A repair-replace strategy based on usage rate for items sold with a two-dimensional warranty[J]. Reliability Engineering & System Safety, 2009，94(2):611-617.

[16] ISKANDAR B P, MURTHY D N P,JACK N. A new repair-replace strategy for items sold with a two-dimensional warranty[J]. Computers & Operations Research, 2005，32(3):669-682.

XU Dekai:Postgraduate;Department of Management and Economics, Tianjin University,Tianjin 300072, China.

Two-dimensional Extended Warranty Strategy Based on Non-periodic Preventive Maintenance

XUDekai

A non-periodic preventive maintenance based on reliability was established to optimize the extended warranty cost. It built two-dimensional extension of product cost model and product cost optimization. The effectiveness of the model is verified by an example and the parameters affecting the model results are evaluated by sensitivity analysis.The results showed that the strategy in this paper could effectively reduce the corresponding extended warranty cost under the condition that the boundary parameters of the guarantee period are determined.

two-dimensional warranty; non-periodic preventive maintenance; extended product warranty

2095-3852(2016)06-0708-04

A

2016-06-10.

国家自然科学基金项目(71171142).

F270

10.3963/j.issn.2095-3852.2016.06.014

收稿日期：徐德凯(1990-)，男，河南安阳人，天津大学管理与经济学部硕士研究生.