基于起降架次的民航事故征候非线性回归预测

王燕平，朱金福，高宁煜

(南京航空航天大学 民航学院,江苏 南京 210016)

基于起降架次的民航事故征候非线性回归预测

王燕平，朱金福，高宁煜

(南京航空航天大学 民航学院,江苏 南京 210016)

针对民航事故征候预测准确性不足的问题，首先，从事故征候数逐年变化趋势的分析着手，将机场起降架次作为民航业务规模衡量指标，深入探究起降架次对事故征候数的影响。然后，利用三次指数平滑法对起降架次随时间的变化趋势进行预测，在此基础上对事故征候数随航空器起降架次的变化规律进行非线性回归分析，建立基于起降架次的事故征候非线性回归预测模型，并以2000—2015年民航数据为基础，验证预测模型的准确性并根据预测结果提出相关安全管理建议。

民航事故征候；预测；起降架次；三次指数平滑；非线性回归

民航安全管理体系(SMS)要求对安全信息进行采集、分析，构建以风险预警管理、反馈控制的安全管理机制[1]。要对未来的安全状态要做到心中有数，则需要更精准的预测，以便在事故和重大事故发生前及时采取预防控制措施降低风险和减少损失。有效预测不仅能减少经济损失，还对民航安全管理的发展具有一定意义。我国民航技术和管理水平的加速提升使民航安全数据也快速增长，民用航空器事故征候的预测研究已成为民航安全研究的一项重要内容。民航行业中事故征候、事故和重大事故数量之间存在一定的比例关系，当事故征候累积到一定数量时，事故发生的概率会迅速增大，所以事故征候数反映着事故发生的概率。从2010年伊春空难以来，国内民航已连续安全运行6年，接近历史最好的安全纪录[2]，但同时各种不安全因素逐步累积，安全心理防线有所松懈，发生不安全事件甚至安全事故的可能性也在增大。刘刚等[3]将灰色预测与马尔可夫预测两种方法相结合，建立灰色马尔可夫预测模型对世界民航事故进行预测。罗帆等[4]运用灰色预测方法建立事故征候数的灰色预测模型，并对未来3年的事故征候数进行预测。王永刚等[5]运用灰色模型对2001—2004年事故征候的实测统计数据进行分析。同时国外的FULLWOOD等[6]运用线性回归对航空安全趋势进行了预测。王永刚等[7-8]将灰色预测与神经网络结合组成串联组合预测模型，并进行了残差反馈，并对以多种方法为单项模型组成的事故征候最优变权组合预测模型进行了研究。

现有预测研究克服了传统预测方法需要大量数据和数据关系拟合不当的弊端，但其都是以时间为自变量直接预测事故、事故征候数，而时间并不能包含所有信息，因此信息的丢失造成预测的准确性不足。笔者针对这一不足，在考虑事故征候数逐年变化的趋势上，探究民航运输机场起降架次对事故征候数的影响，分别运用三次指数平滑方法和非线性回归预测方法，寻求起降架次与时间、民航事故征候数及起降架次之间的关系。以2000—2015年的运输机场航空器起降架次和民航事故征候统计数据[9-10]为例，建立更准确的民航事故征候预测模型，预测2016—2017年的事故征候数，并根据预测结果提出相关安全管理建议。

1 三次指数平滑预测起降架次模型

1.1 起降架次的趋势分析

收集2000—2015年运输机场年起降架次的历史数据，如表1所示。在此基础上建立起降架次预测模型，其中以2000—2014年起降架次作为建模数据集，以2015年的起降架次作为验证集。历史数据序列呈现二次曲线上升趋势，如图1所示，因此选用三次指数平滑法对起降架次的变化趋势进行分析和预测。

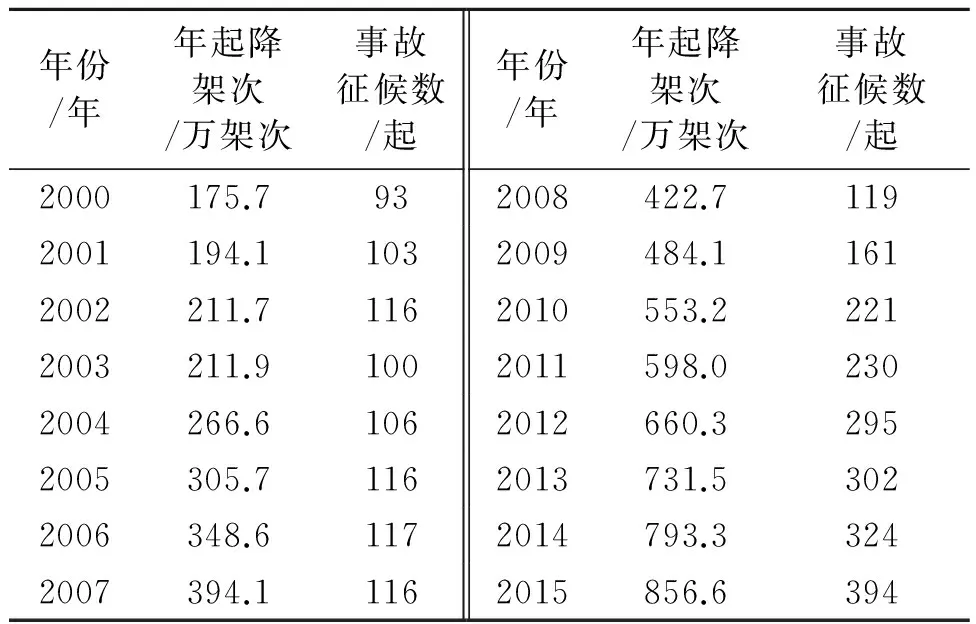
表1 2000 —2015年中国民航事故征候数与运输机场年起降架次统计数据

注：起降架次是指报告期内在机场进出港飞机的全部起飞和降落次数，起飞、降落各算一架次。

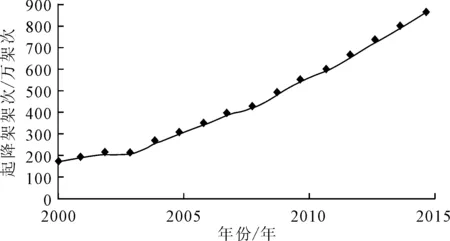
图1 2000—2015年全国运输机场航空器起降架次变化趋势

1.2 三次指数平滑预测模型

指数平滑法是在加权平均法的基础上发展而来，将数据的重要程度处理为按时间的远近呈非线性递减。指数平滑法虽存在预测数据滞后的现象，但对于短期预测仍然具有较高的使用价值[11-13]。

设t个原始数据组成的时间序列为：X=[X(1)，X(2)，…，X(t)]，则三次指数平滑模型为：

(1)

三次指数平滑在一次和二次指数平滑的基础上再进行平滑处理，计算公式为：

(2)

(3)

(4)

(5)

(6)

(7)

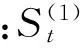
1.3 三次指数平滑法预测年起降架次

采用2000—2014年的15个原始数据作为建模数据集，建模数据集组成的时间序列为：X=[X(1)，X(2)，…，X(15)]，选择前3年实际值的平均值作为初始值。

通过试算得出平滑指数α值取0.4时预测精度最佳。由式(5)～式(7)计算起降架次预测所需的各项参数值，计算结果如表2所示。

2001—2014年的预测值分别根据前1年的平滑系数、前1年份的数据，取T=1计算，由式(1)可得2001—2014年的预测模型为：

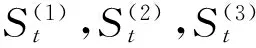
将2015年的数据作为验证集对所建模型的预测结果进行验证。预测2015年的起降架次数据，在2014年数据的基础上取T=1得到：

起降架次预测值与实际值的对比如图2所示。由图2可知，针对我国运输机场航空器年起降架次的三次指数平滑法预测精度较高，预测值与实际值基本相符。同理在2015年的数据基础上取T=1、T=2代入模型求得2016、2017年的起降架次预测值分别为：

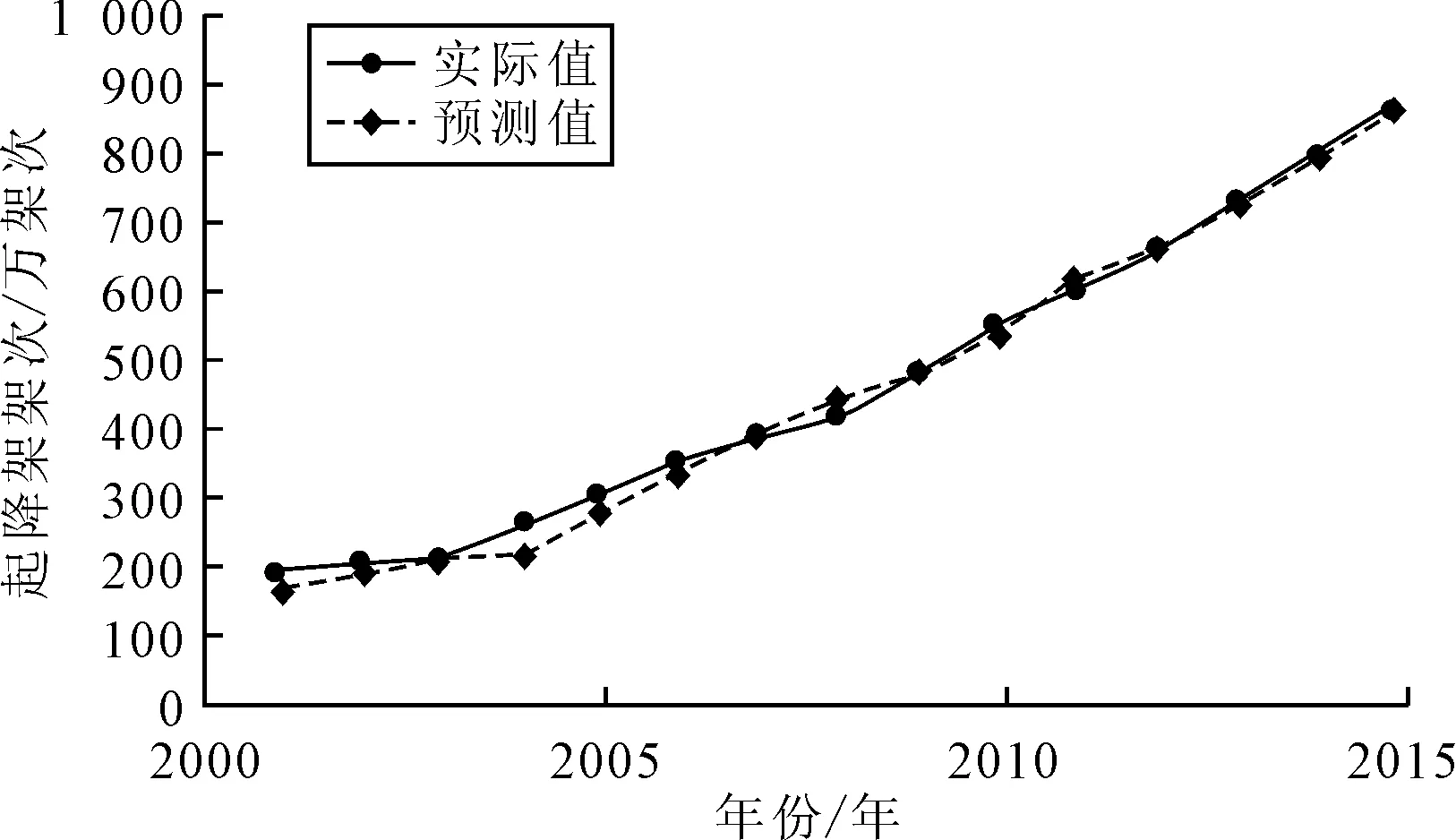
图2 起降架次预测值与实际值的对比图

2 非线性回归模型预测事故征候数模型

2.1 建立非线性回归预测模型

2.1.1 描绘事故征候数与年起降架次的散点图

根据2000—2014年的年起降架次与事故征候数的15组原始数据，将年起降架次按递增顺序排列，并将事故征候数与之对应排列，如表3所示。事故征候数与年起降架次的散点图如图3所示，可看出事故征候数和相应起降架次的分布状况。从图3散点图可以直观地看出数据的特征是波动上升的，年起降架次与事故征候数之间具有一定相关性，且可以判断二者具有非线性相关关系，对应这种关系特征，采用对非线性相关关系的数据有较强处理能力的非线性[14-15]回归来建立基于年起降架次的民航事故征候数预测模型。

2.1.2 非线性回归模型的线性逼近

非线性回归模型的线性逼近原理是用泰勒级数展开式去近似代替非线性回归模型，并通过多次迭代来修正回归系数，以期得到最佳回归系数，使原模型的残差平方和达到最小。非线性回归的线性逼近过程采用SPSS 17.0软件的相关分析模块进行处理，由于SPSS尚无法智能自动拟合所需曲线，故需要用户估计方程中各项系数的迭代初始值[16]。在回归模型与初始值的选择上，根据起降架次-事故征候数的散点图特征分析，选用指数模型作为初始模型，设方程模型为：

y=cedx

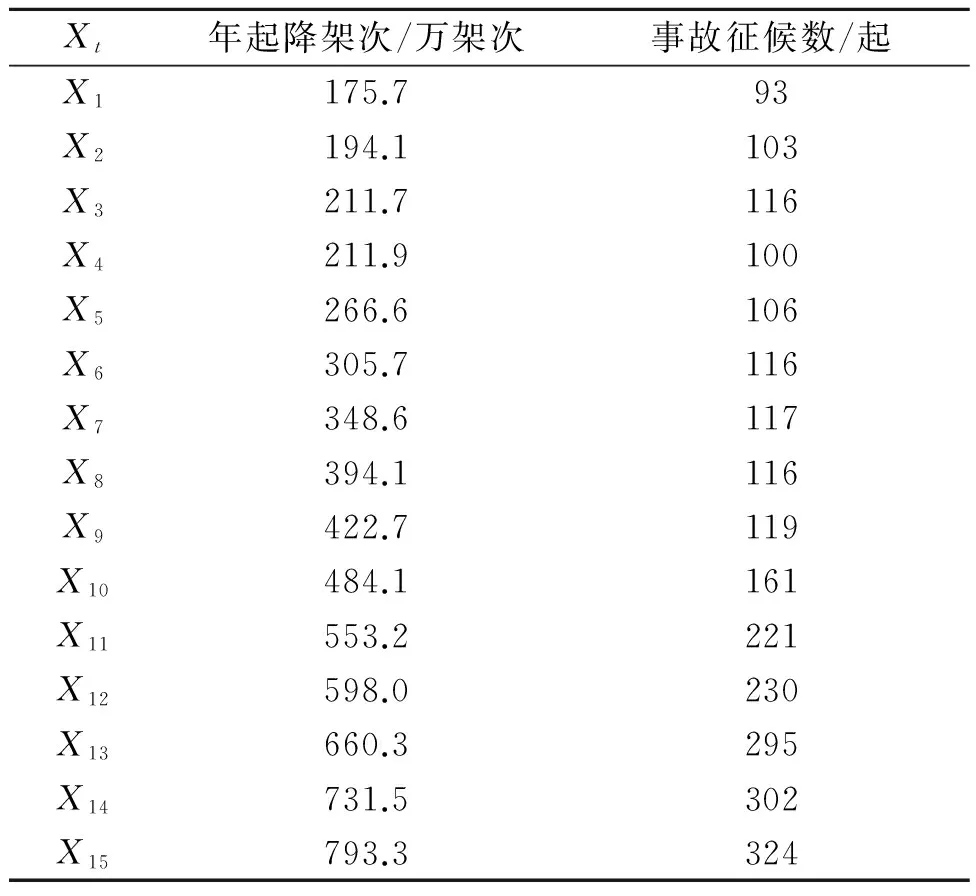
表3 起降架次与事故征候数量相关表

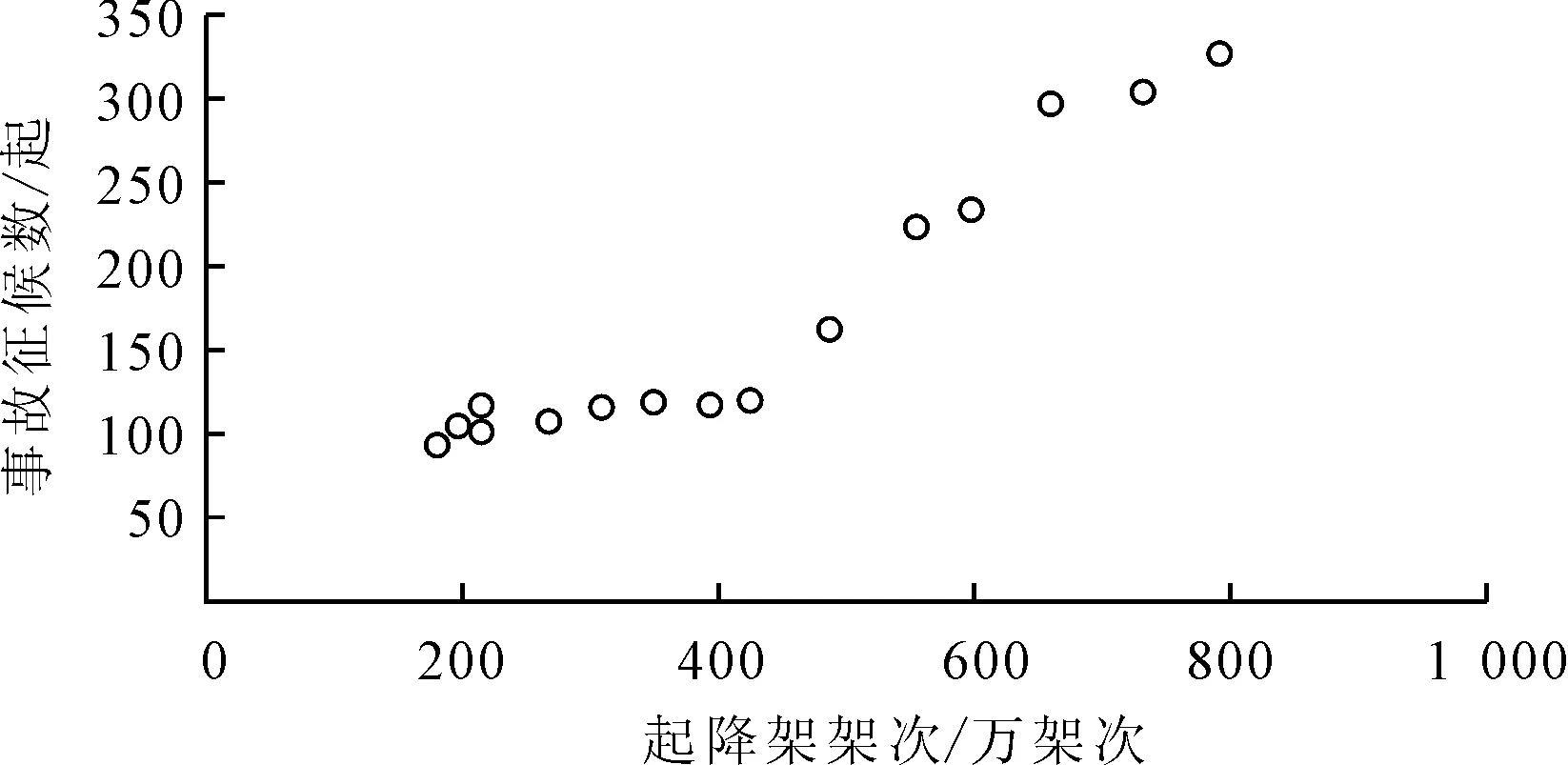
图3 2000—2014年事故征候数与年起降架次的散点图

式中：y为因变量事故征候数；x为自变量起降架次。

通过线性变换和最小平方法求得参数c、d的初始值分别为c=61.000，d=0.002，根据设定的方程模型和参数初始值通过SPSS的相关分析模块得到以下分析结果，分别如表4和表5所示。

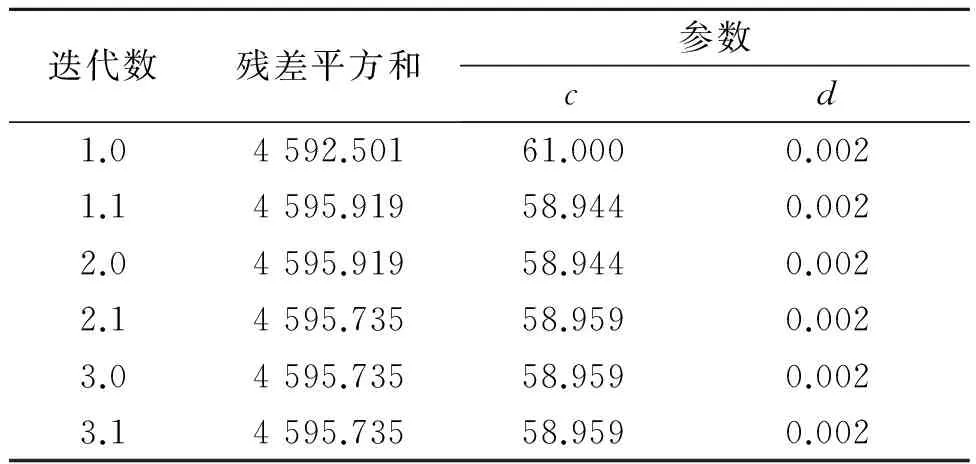
表4 非线性迭代历史记录

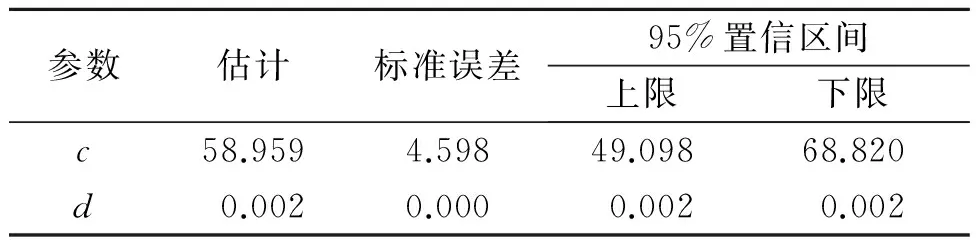
表5 回归输出参数估计值

由表4和表5可知，输入方程模型和参数初始值后，经过6次将“参数估计值”代入“损失函数”的迭代运算后，相邻两次方程残差平方和的差值小于1.00×10-8，满足要求，此时系统取得最优解并终止运算。所得到参数估计值c=58.959，d=0.002，所得到的非线性模型表达式为：y=58.959·e0.002x。所得方程的判定系数R2=0.969，说明拟合得到的函数能够较好地表达自变量(起降架次)和因变量(事故征候数)之间的关系。

2.2 非线性回归预测模型的预测结果

根据上述非线性预测模型得到的预测结果输出如表6所示。对2000—2014年基于起降架次的事故征候数预测值与实际值的对比如图4所示，可知所得非线性回归预测模型能够大致反映事故征候数随起降架次的变化趋势，尤其对近几年的数据变化趋势拟合更为接近。

2.3 不同预测方法的结果对比

通过将预测准确性较高的灰色神经网络预测模型与笔者预测模型作对比，验证所构建预测模型的优势和实用性，两种预测模型的对比如表7所示。从表7可看出，灰色神经网络模型预测近几年的事故征候结果误差较大，该方法预测的数据变化趋势远远低于实际数据增长的趋势；基于起降架次的非线性回归模型对事故征候数的预测，既准确拟合了起降架次与时间序列之间的关系，又分析了起降架次与事故征候数之间的非线性关系，因此包含了更全面的信息，对事故征候数(尤其近期)的预测更为准确。

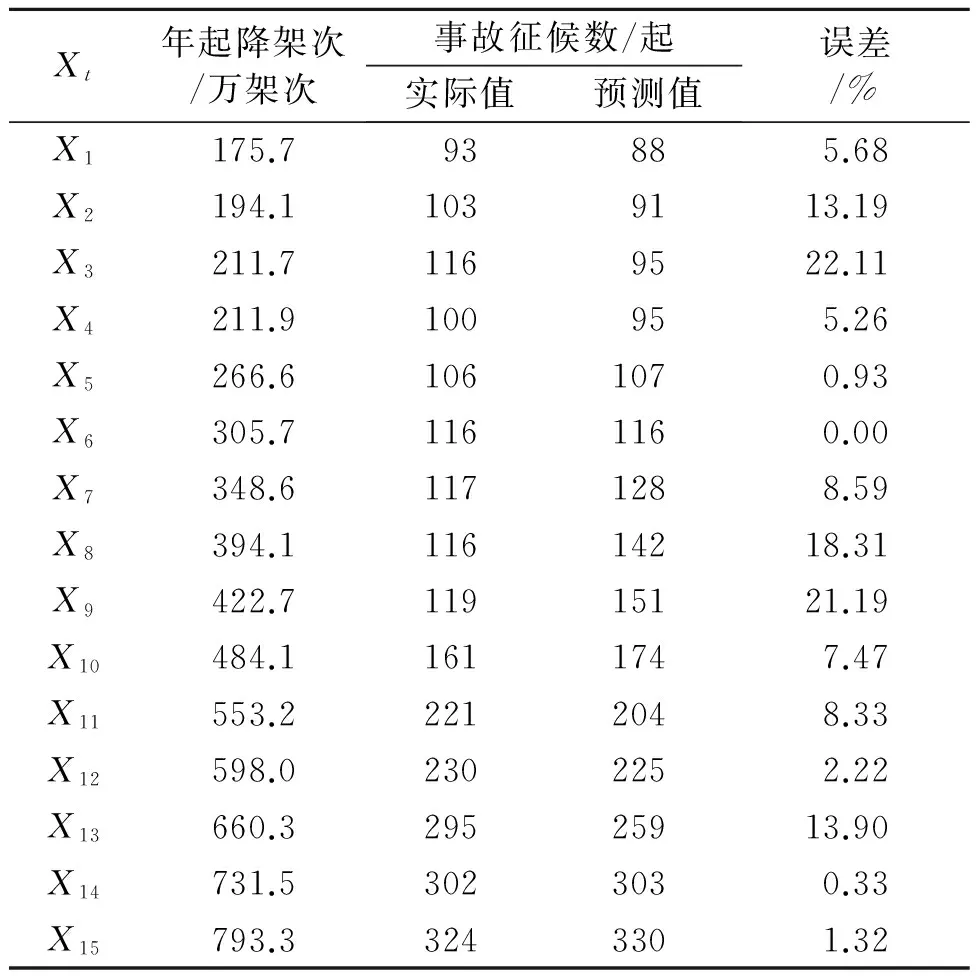
表6 事故征候数的非线性回归预测表

3 未来事故征候预测及结果讨论

已知上述三次指数平滑法对2016和2017年我国运输机场起降架次的预测值分别为929.91万架次和1 003.82万架次，则由上述非线性回归预测模型可得到2016和2017年全国民航事故征候数量预测值分别为378.7起和439.0起。可见2016年事故征候数预测值378.7起比2015年的394.0起略有下降，说明民航当局对2015年的民航安全状况有所警觉，并采取了相应的安全管理手段和控制措施，使2016年的事故征候数量得到控制。2017年事故征候数量继续攀升，一方面因为民航业务规模增大，起降架次增加使事故征候数增加，另一方面民航局所采取的安全管理手段和控制措施具有时效性，并非长久有效，此时管控措施对事故征候数的缓解效果低于起降架次的增多所带来的风险。

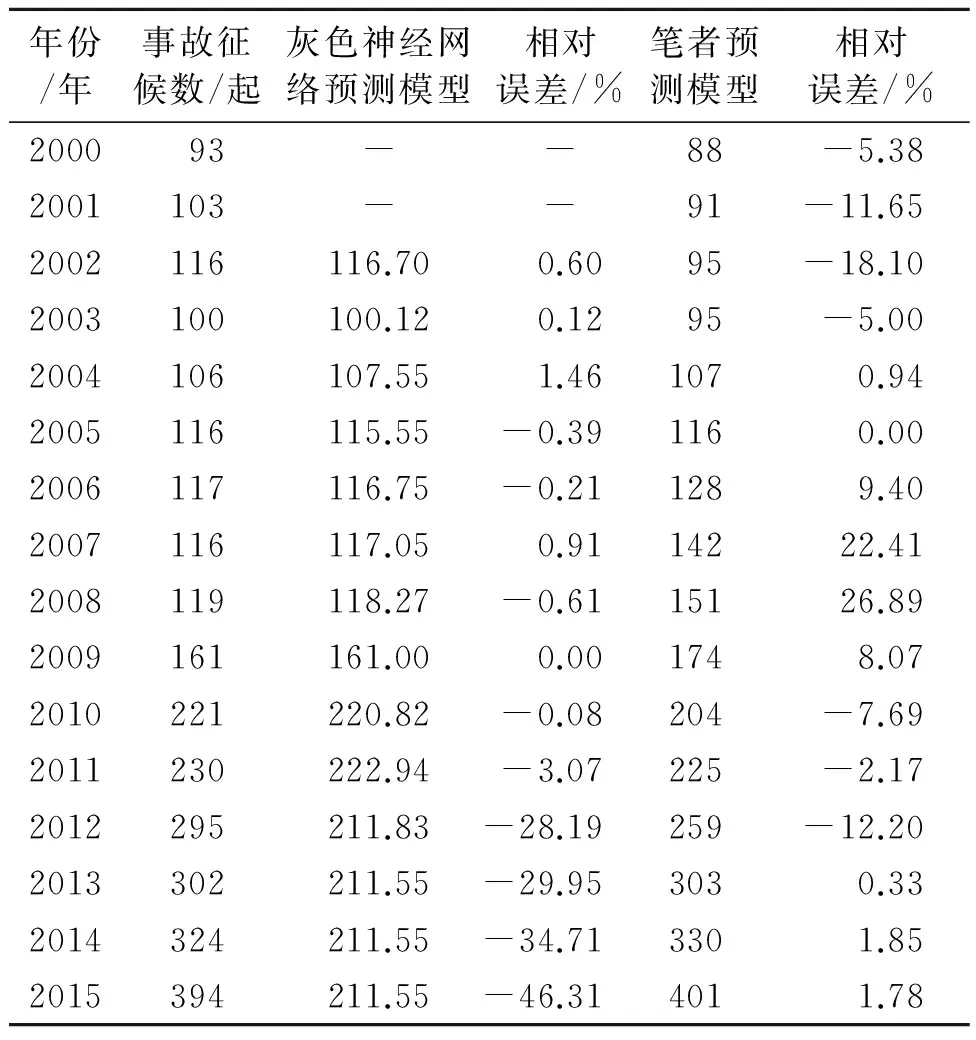
表7 不同模型的事故征候数预测对比表

因此民航当局应根据事故征候数量的预测情况实施有效的安全运行管理，坚持长期累积，持续采取相应的控制措施，以期之后的事故征候数能够有所下降，从而使发生事故的风险降低。强化安全管理是降低事故征候、事故发生概率的有效途径，当发现事故征候数有增加的趋势时，应采取更严厉的安全管理措施来加以控制[17-18]。

4 结论

民航事故征候数随着民航业务量的增加而增加，航空器起降架次作为民航业务量的一个重要衡量指标，与事故征候数有重要联系并对其产生不容忽视的影响。笔者首先对随时间变化的起降架次进行预测，在此基础上将起降架次作为自变量，确定起降架次对事故征候数的影响，建立基于起降架次的事故征候数预测模型，相较于只通过时间推移进行预测，该模型分析了更多的信息且具有更高的准确性。

通过对预测结果的分析可知，采取相应安全管理措施具有重要性和必要性，强化安全管理是降低事故发生率的有效途径，当发现事故征候数有增加的趋势时，应采取更严厉的安全管理措施加以控制。随着SMS在我国的应用发展，民航安全管理水平不断提高，对起降架次与事故征候数之间的关系会造成影响，笔者尚未将安全管理水平等因素的影响考虑在预测模型内，有待后期继续分析完善。

[1] 贾贵娟,汪洪蛟.空中交通安全风险管理系统的构成及运行流程[J].武汉理工大学学报(信息与管理工程版),2008,30(5):827-830.

[2] 中国民用航空局.民用航空器事故征候：MH/T2001—2015[S/OL].[2016-09-09].http://safety.caac.gov.cn/admin/newsab/outview.do?pk=100000313307796.

[3] 刘刚,朱金福.基于灰色新陈代谢马尔可夫模型的飞行事故预测[J].中国安全科学学报,2007,17(5):17-20.

[4] 罗帆,熊伟.民航事故征候的灰色预测[J].价值工程,2008,27(1):1-3.

[5] 王永刚,吕学梅.民航事故征候的关联度分析和灰色模型预测[J].安全与环境学报,2006,6(6):127-130.

[6] FULLWOOD R R, HALL R E, MARTINEZ-GURIDI G, et al. Relating aviation service difficulty reports to accident data for safety trend prediction[J]. Reliability Engineering & System Safety,1998,60(1):83-87.

[7] 王永刚,李辉.基于灰色神经网络的民航事故征候预测模型研究[J].中国安全科学学报,2012,22(3):10-15.

[8] 王永刚,郑红运.基于最优变权组合模型的航空运输事故征候预测[J].中国安全科学学报,2013,23(4):26-31.

[9] 中国民用航空局.2015年民航行业发展统计公报[R/OL].(2016-05-30)[2016-09-09].http://www.caac.gov.cn/XXGK/XXGK/TJSJ/201605/t20160530_37643.html.

[10] 中国民用航空局.中国航空运输发展统计报告[R].[S.l.]:中国民用航空局,2015.

[11] 刘思峰.预测方法与技术(第二版)[M].北京：高等教育出版社,2005:54-64.

[12] 朱庆明,张浩.三次指数平滑法在煤矿事故预测中的应用研究[J].中国安全生产科学技术,2012,8(4)：103-106.

[13] 郑小平,高金吉.事故预测理论与方法[M].北京：清华大学出版社,2009:129-161.

[14] 张进春,吴超.基于偏最小二乘回归的焦炭热性质非线性预测模型[J].中南大学学报(自然科学版),2011,42(5)：1406-1412.

[15] 甘蓉蓉.人口预测的方法比较：以生态足迹法、灰色模型法及回归分析法为例[J].西北人口,2010,31(1)：57-60.

[16] 杨维忠,张甜.SPSS统计分析与行业应用案例详解[M].北京：清华大学出版社,2005:54-64.

[17] 张兆宁,冯守乐,王莉莉.民航安全管理与风险管理的关系[J].航空安全,2011(4)：61-63.

[18] 霍志勤.本质安全论在民航安全管理中的应用[J].中国民航大学学报,2010,28(3)：49-53.

WANG Yanping:Postgraduate; School of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China.

Nonlinear Regression Forecasting of Civil Aviation IncidentsBased on Taking off and Landing Sorties

WANGYanping,ZHUJinfu,GAONingyu

Based on the analysis of the trend of the number of incident and incident, firstly, the paper takes the airport takeoff and landing as the index of civil aviation business scale, and probes into the impact of the number of movements on incident number.Then based on using cubic exponential smoothing to predict the trends of taking off and landing sorties over time, it makes nonlinear regression analysis of incidents' trend beside movements，thus establishes a non-linear regression forecast model. It uses the 2000-2015 civil aviation incidents number and taking off and landing sorties as data base to verified accuracy of the prediction model, and making recommendations about safety management.

civil aviation incidents; forecasting; taking off and landing sorties; cubic exponential smoothing method; nonlinear regression

2095-3852(2016)06-0672-06

A

2016-06-09.

南京航空航天大学创新基地(实验室)开放基金项目(kfjj20150711).

X928.03

10.3963/j.issn.2095-3852.2016.06.007

收稿日期：王燕平(1992-)，女，安徽宿州人，南京航空航天大学民航学院硕士研究生.