基于遗传算法的海上搜索力量优化研究*
2017-01-11胡宏启陈建华
胡宏启 陈建华
(海军陆战学院 广州 510431)
基于遗传算法的海上搜索力量优化研究*
胡宏启 陈建华
(海军陆战学院 广州 510431)
在实际的海上搜索工作中,海上搜索区域由若干个分散的子区域组成,而搜索主体通常也不只是一个,研究多目标区域条件下如何配置搜索力量,以期达到最优的搜索效果,具有较大的实践意义。从分析搜索力量最优化分配的角度入手,基于遗传算法,构建搜索力分配的计算模型,并通过实例,对模型的有效性进行检验验证。
搜索; 遗传算法; 模型
(Naval Marine Academy, Guangzhou 510431)
Class Number TP391
1 引言
随着中国经济的发展,海上活动日益频繁,海难事故时有发生,严重威胁着海上人员生命财产安全,对海上遇险船舶、人员实施及时的搜索对于减少生命、财产损失具有十分重要的意义。2014年发生的马来西亚航空MH370客机失联事件以及韩国“岁月号”客轮沉没事件让公众更加清楚认识到海上搜救的重要性[1]。海上搜索是一项较为复杂的工作,涉及到很多计算问题,海难事故发生时,对搜索力量进行优化分配,增大搜索成功概率,可以为搜索计划的制定提供科学的理论依据。
2 最优搜索问题的描述
在海上搜索过程中,参与搜索的人员数量、观察器材的效果、耗费的搜索时间(或观察次数)、搜索航程或搜扫面积等等统称为搜索力。搜索力在时间、空间上的分配方式,称为搜索力的配置或搜索计划。假设目标的位置在搜索区域内的分布是已知的,为了发现目标,就必须在目标出现概率大的地方,多配置一些搜索力。根据所知道的目标位置的分布律,对所拥有的有限的搜索力,在一定的成本约束下如何分配,才能使发现目标的概率最大,这就是搜索力的最优配置问题,也就是最优搜索计划问题[2]。
海上搜索行动能否取得成功主要受两个因素的影响: 1) 搜索者必须在可能包含目标的区域中搜索, 2) 搜索者在搜索区域内必须具有探测发现搜索目标的能力,即搜索者所配备的探测器能以一定探测概率在搜索区域内探测到该目标。搜索成功概率(Probability of Success,POS)是发现目标的可能性,它依赖于两个概率[3~4]:
1) 搜索区域包含目标的概率,简称包含率(Probability of Containing,POC)。
2) 如果搜索目标在该搜索区域内,搜索者探测到目标的概率,简称探测率(Probability of Detection,POD)。
POS的计算公式为
POS=POC×POD
与POD相比,POS能真正衡量搜索行动的效率。实际搜索行动中,POS的值处在0~1之间。不同的POC和POD组合产生0~1之间任意的POS值。根据目标位置及其移动路径的概率分布,可以获得指定搜索区域的POC。而探测函数则给出了搜索者在指定搜索区域中搜索的POD。因此海上最优搜索的目标可表示为,在最可能搜索区域之上最有效地分配有限且昂贵的搜索资源使得搜索行动中POS的值达到最大。
探测函数是以搜索力为自变量的探测概率。搜索力可以是搜扫面积、时间、轨迹路径或者任何适于给定搜索的物理量。定义于J的探测函数形如b:J×[0,∞)→[0,1],搜索的总区域为J,b(j,z)表示目标位于搜索子区域j时,把z量的搜索力施加到该区域而探测到目标的条件概率,在这里假定在区域j的探测概率仅仅取决于施加于该区域的搜索力总数,而与搜索力施加的方式无关[5]。
探测函数给我们提供了一种根据探测到目标的概率来分析搜索效果的方法。设p为目标在J上的概率分布,假定某一搜索计划把f(j)量的搜索力施加于区域j,那么目标位于区域j且由搜索力f(j)探测到该目标的概率为p(j)b(j,f(j))。探测到目标全概率为
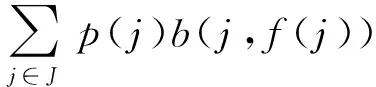
所付出的搜索力总数为∑f(j)。
一般情况下,能够用于搜索的搜索资源是有限的,总希望在物力范围内(即在费用约束条件下)优化探测到目标的概率。定义于J的费用函数形如C:J×[0,∞)→[0,∞)。由此,c(j,z)表示把搜索力z施加于单元j的费用。经常地c(j,z)=z(j∈J,z≥0),这意味着搜索费用由搜索力度量。此外,搜索费用也可不由搜索力度量。比如,搜索力可由轨迹路程度量,而费用则由金钱度量,搜索力与费用的度量取决于实际的搜索问题。
对于离散型分布的多区域目标,令F为该空间内分配函数的集合,对于f∈F,P[f]是与分配函数f对应的探测到目标的概率。C[f]是与f对应的搜索费用。假设K为搜索费用的限定值。基本搜索问题是找到f*∈F,使得
C[f*]≤K,P[f*]=max{P[f]:f∈F及C[f]≤K}
f*称为对应于费用K的最优分配函数。
3 遗传算法简介
遗传算法是模拟生物进化过程的计算模型。遗传算法作为一种新的全局优化搜索算法,以其简单通用、鲁棒性强、适于并行处理以及应用范围广等显著特点,奠定了它作为21世纪关键智能计算之一的地位[6]。
生物的遗传物质的主要载体是染色体,DNA是其中最主要的遗传物质,而基因又是控制生物性状的遗传物质的功能单位和结构单位。复数个基因组成染色体,染色体中基因的位置称作基因座(locus),而基因所取的值又叫做等位基因(alleles)。基因和基因座决定了染色体的特征,也就决定了生物个体的性状。此外,染色体有两种相应的表示模式,即基因型和表现型。所谓表现型是指生物个体所表现出来的性状,而基因型指与表现型密切相关的基因组成。同一种基因型的生物个体在不同的环境条件下可以有不同的表现型,因此表现型是基因型与环境条件相互作用的结果。在遗传算法中,染色体对应的是数据或数组,在标准的遗传算法中,这通常是由一维的串结构数据来表现的。串上各个位置对应上述的基因座,而各位置上所取的值对应上述的等位基因。遗传算法处理的是染色体,或者叫基因型个体(individuals)。一定数量的个体组成了群体(population),也叫集团。群体中个体的数目称为群体的大小(population size),也叫群体规模,而各个体对环境的适应程度叫做适应度(fitness)[7]。
遗传算法是具有“生成+检测”的迭代过程的搜索算法。它的基本处理流程如图1所示。

图1 遗传算法流程图
4 算法应用
案例假设,某商船海上失事,人员落水,海水温度20℃,根据水温与生存时间的关系,落水人员在海水中生存的极限时间为10小时,除去搜救船只到达搜索区域的时间,搜索的生还者的有限时间为8小时,根据目标分布概率的特点将搜索区域分为6个矩形子区域,长、宽分别为(3海里,2海里),(5海里,3海里),(5海里,3海里),(5海里,4海里),(5海里,5海里),(5海里,3海里),根据目标的概率分布,初步确定各个子区域的概率分布依次为0.05,0.25,0.15,0.2,0.25,0.1,采用搜救船只对搜索区域进行搜索,其搜索行进速度为18节,扫视宽度为1海里。
本问题采用符号编码方式,案例给出的有限的搜索时间为8小时,可将搜索时间做n等分,n值大小取决于计算所需的精度,搜索时间分别分布于6个搜索区域中,对n等分的时间进行编码,形如α1α2α3α4α5…αn,在此取n=480,即将时间细化至每一分钟。
码串即为遗传算法中的染色体,αk(1≤k≤n)为染色体上的一个基因,每一码串均属于问题解空间的一个解,每一基因αk∈(1,2,3,4,5,6),问题的目标使探测到海上落水人员的概率取得最大值,因此可取探测到落水人员的全概率为适应度函数。
用mj,j∈(1,2,3,4,5,6)表示每一个码串中基因取值为j的基因数目,那么m1表示属于第一个搜索区域的基因数,m1/60即为分配在第一个搜索区域上的搜索时间,参考文献[8],计算出探测函数:
b(j,z)=b(j,mj)=1-e-vmjω/60Aj
则算法的适应度函数为
1) 初始化种群
随机产生50个码串作为第一代染色体。
2) 复制操作
将50个父代染色体全部参与复制到子代,参与选择。
3) 交叉操作
设置交叉概率PC=0.25,取每个码串的前120位进行交叉。
4) 变异操作
设置变异概率为0.01,在此设置5位变异数字,随机取5位数字进行变异操作。
5) 遗传终止条件
遗传次数最小为50,最大为500,适应度函数差距小于0.001时可以提前终止。
利用Matlab软件编写程序[9~10],进行模型检验,部分代码如下:
R=randint(100,480,[1 6]);%初始化种群
RR=R;
for i=1:1:50
RR(51:100,:)=RR(1:50,:); %复制操作
for i0=1:2:49 %交叉操作,交叉概率0.25
jc=RR(50+i0,1:120);
RR((50+i0),1:120)=RR((51+i0),1:120);
RR((51+i0),1:120)=jc;
end
for i1=1:1:50 %变异操作,变异概率0.01
RR((50+i1),476:480)=randint(1,5,[1 6]);
end
for i2=1:1:100
C(i2)=gl(RR(i2,:)); %计算适应度
end
[B,ind]=sort(C,2,'descend');
for i3=1:1:50
RR(i3,:)=RR(ind(i3),:);
end
end
gl(RR(1,:)) %gl为调用的概率计算函数
计算出最大概率为0.80。
5 结语
本文从海上搜索的特点和基本原则出发,给出了最优搜索问题的目标函数,运用遗传算法建立了搜索力的优化分配模型,使其具有较好的符合性。实例解算证明了该算法简便、搜索质量高、速度快,适于解决复杂的搜索力量优化分配问题。
[1] 吴翔.海上搜救中发现概率的研究[J].中国安全生产科学技术,2015,11(1):28-30.
[2] [苏]B·A阿勃楚克.搜索目标法[M].北京:中国系统工程学会军事系统工程委员会,1982:303-308.
[3] 李杰.海上搜救辅助决策系统设计及应用[D].哈尔滨:哈尔滨工程大学,2011:14-19.
[4] 肖方兵.海上搜救决策支持系统关键技术的研究[D].大连:大连海事大学,2011:19-21.
[5] 劳伦斯D.斯通.最优搜索理论[M].吴晓峰,译.北京:海潮出版社,1990:7-23.
[6] 戴军.基于遗传算法的水下机器人模糊控制器设计[D].哈尔滨:哈尔滨工程大学,2002:23-26.
[7] 蔡自兴.人工智能及其应用[M].北京:清华大学出版社,2013:160-169.
[8] 张之駓.搜索论[M].大连:大连舰艇学院,1988:31-36.
[9] 许丽佳.MATLAB程序设计及应用[M].北京:清华大学出版社,2011:32-52.
[10] 孙蓬.MATLAB基础教程[M].北京:清华大学出版社,2011:79-101.
Maritime Search Power Optimization Research Based on Genetic Algorithm
HU Hongqi CHEN Jianhua
In actual maritime search work, the search area is composed of several scattered sub regions, and usually there is not just one searching unit, researching how to configure the search power when there are some areas to achieve the optimal search effect is of great practical significance. In this text,how to configure the search power is analyzed. Based on the genetic algorithm, a search power distribution calculation model is builded, and the validity of the model is verified through an example.
search, genetic algorithm, model
2016年6月10日,
2016年7月29日
胡宏启,男,硕士研究生,研究方向:海军兵种战术建模与仿真。陈建华,男,硕士,教授,研究方向:战术建模与仿真、人工智能、软件工程。
TP391
10.3969/j.issn.1672-9730.2016.12.023
