基于上升沿波形配对的信号分选方法研究*
2017-01-11吴惟诚潘继飞
吴惟诚 潘继飞 刘 鑫
(1.电子工程学院雷抗系503室 合肥 230037)(2.电子工程学院雷抗系505室 合肥 230037)
基于上升沿波形配对的信号分选方法研究*
吴惟诚1潘继飞1刘 鑫2
(1.电子工程学院雷抗系503室 合肥 230037)(2.电子工程学院雷抗系505室 合肥 230037)
针对当前分选算法中普遍存在增批、漏批的问题,提出了基于上升沿波形配对的分选方法。该方法通过Hilbert法提取辐射源信号的包络波形,并采用三次样条插值法进行拟合,提取具有指纹特性的包络上升沿波形特征,利用Hausdorff距离函数作为相似性度量的方法进行波形配对。通过三组实验,验证了基于上升沿波形配对分选方法的有效性,以及上升沿波形的选择和采样点数对该方法的影响。
信号分选; 脉冲包络; 上升沿波形; Hausdorff距离
(1. Room 503, Department of Radar Countermeasure, Electronic Engineering Institute, Hefei 230037)(2. Room 505, Department of Radar Countermeasure, Electronic Engineering Institute, Hefei 230037)
Class Number TN974
1 引言
辐射源信号分选方法的核心是特征提取,所选择特征的可分离性决定了分选方法的有效性,当前主要采用的是脉间参数特征和脉内细微特征[1],而分选算法普遍存在增批、漏批的问题。因此,基于个体识别结果的方法才能实现有效的信号分选,需要提取辐射源信号的指纹特征作为分选的依据。指纹特征常用于辐射源的个体识别,且有不少研究成果:秦长海[2]、王宏伟[3]等通过提取出的已知雷达脉冲包络前沿波形进行统计,得到一条能代表特定雷达辐射源的“标准”前沿波形曲线,然后被测量雷达信号的脉冲包络前沿波形与“标准”前沿波形曲线的相像程度进行对比,实现个体识别。陈韬伟[4]等利用信号的围线积分双谱来提取无意调相特征作为指纹识别的依据。张国柱[5]等利用Morlet复小波进行包络分析,利用平滑滤波及差分方法提取包络的上升时间、下降时间及包络顶降作为识别依据。
传统方法是先对信号分选再进行识别,分选结果往往存在许多问题。而基于识别的分选方法是先对信号进行个体识别再分选,这样的方法更加有效,但这方面的研究并不是很多。另外,由于噪声干扰、测量误差等的存在,在实际信号的分选过程中,参数特征的准确性受到了极大的限制。因此,可以直接从信号最直观表现形式—波形入手,通过对信号进行某种变换或映射,提取具有指纹特性的波形,再利用相似性度量的方法进行波形配对,在不需要先验知识支撑下,实现信号分选。
2 上升沿波形的指纹特性
2.1 信号包络的指纹特性
由于任何单个雷达辐射源内所用的电子元器件均存在不可避免的误差,且内部机械构造也存在极小的差异,因而在脉冲信号的包络[6]波形上表现出了复杂的非线性特征。也可以说是雷达辐射源信号脉冲包络波形上的差异是不可避免存在的,即便是同一生产厂商在同一时间、同一批次生产出来的相同型号的两部雷达个体也是如此,这样就从硬件的构造上说明了根据信号脉冲包络波形的差异进行雷达辐射源信号分选是具有一定可行性的。
接收到的辐射源信号由于受到噪声干扰、信道衰落和多径效应等的影响,脉冲信号的包络波形在由电磁空间传输到接收天线的过程中,必定会造成失真,使得包络的形状出现起伏和变化,其中对脉冲信号的包络影响最大的是多径效应。而经研究发现在信号的包络各参数特征中,包络的前沿波形是受多径效应影响最小的,而包络的后沿波形及脉宽是受多径效应影响最大的。因此,本文只考虑了从宏观角度对信号的整体包络波形进行研究,避开多径效应带来的影响,选取了信号包络的上升沿作为辐射源个体的“指纹”特征[7],对辐射源信号进行分选。某雷达信号的脉冲包络波形如图1所示。

图1 脉冲包络波形示意图
2.2 上升沿波形的产生机理
信号的包络波形最主要是受脉冲调制器的影响,型号不同的脉冲调制器产生脉冲调制信号的包络波形是不一样的,即使是同一种型号、同一批次生产的脉冲调制器,由于不同调制器个体的电子元器件在组成上的差异,所产生的调制信号的包络也必然是有差别的。也即是说脉冲调制器决定了信号包络的上升沿波形。
在辐射源的发射机组成部分,脉冲调制器是由电源系统、能量存储元件和脉冲形成电路等部分组成,脉冲调制器的性能好坏直接影响脉冲的上升、下降沿波形、脉冲顶部变化情况、脉冲宽度等特征参数,其工作原理为:开关断开期间,储能元件通过限流和旁通元件将电源能量存储其中,开关导通期间,储能元件则向负载放电,从而形成调制脉冲。其基本组成框图如图2所示。

图2 脉冲调制器的基本组成框图
理想情况下的脉冲包络形状为规则矩形,具有陡直的前后沿和平坦的顶部特性,而实际中,器件在工作期间难以避免地会产生寄生参量,如储能电容的容量和峰化电感的大小对脉冲顶降的影响,以及磁控管和储能电容对脉冲上升、下降沿波形的影[8]响等,其中上升沿波形形成的等效电路图如图3所示。

图3 上升沿波形形成的等效电路图
在UL高于门限电压之前,调制管的电流im全部向分布电容C0充电,故UL随时间变化的函数为
(1)
由于磁控管程的门限电压与实际工作电压很接近,而im基本保持不变,如果把脉冲上升沿波形定义为负载电压UL从门限电压Us的10%上升到90%的那段,则有上升沿的时间函数为
(2)
从式(2)可看出,影响包络上升沿的因素主要有2个:电流im和分布电容C0。由文献[9]中分析可知,脉冲顶降随储能电容C和峰化电感L的增大而减小,包络的上升沿波形随分布电容C0和峰化电压UL的减小而变陡。
经过上述分析不难发现,信号包络上升沿波形的产生与脉冲调制器的内部构造密切相关,是雷达辐射源一个重要的指纹特征,因此本文通过提取包络上升沿作为指纹特征,利用波形配对的方法实现辐射源信号分选,以解决当前方法普遍存在的增批、漏批问题。
3 上升沿波形的提取
3.1 脉冲包络的提取与拟合
首先对接收到的脉冲信号进行包络提取与拟合,并对所提的包络波形进行归一化处理,最后提取包络的上升沿部分,通过波形配对来实现信号分选。假设传播通道对接收机的影响很小,忽略多径影响,且接收机带宽足够,确保不会造成包络的失真。利用一台雷达模拟发射样机,产生几种雷达信号样式,具体参数如表1所示。

表1 实验信号的参数表
利用Tektroinx DPO 72004C型数字示波器采集雷达发射机输出的信号,统一采集2500个数据点,利用Hilbert[10]法对每个信号求得包络波形如图4所示。


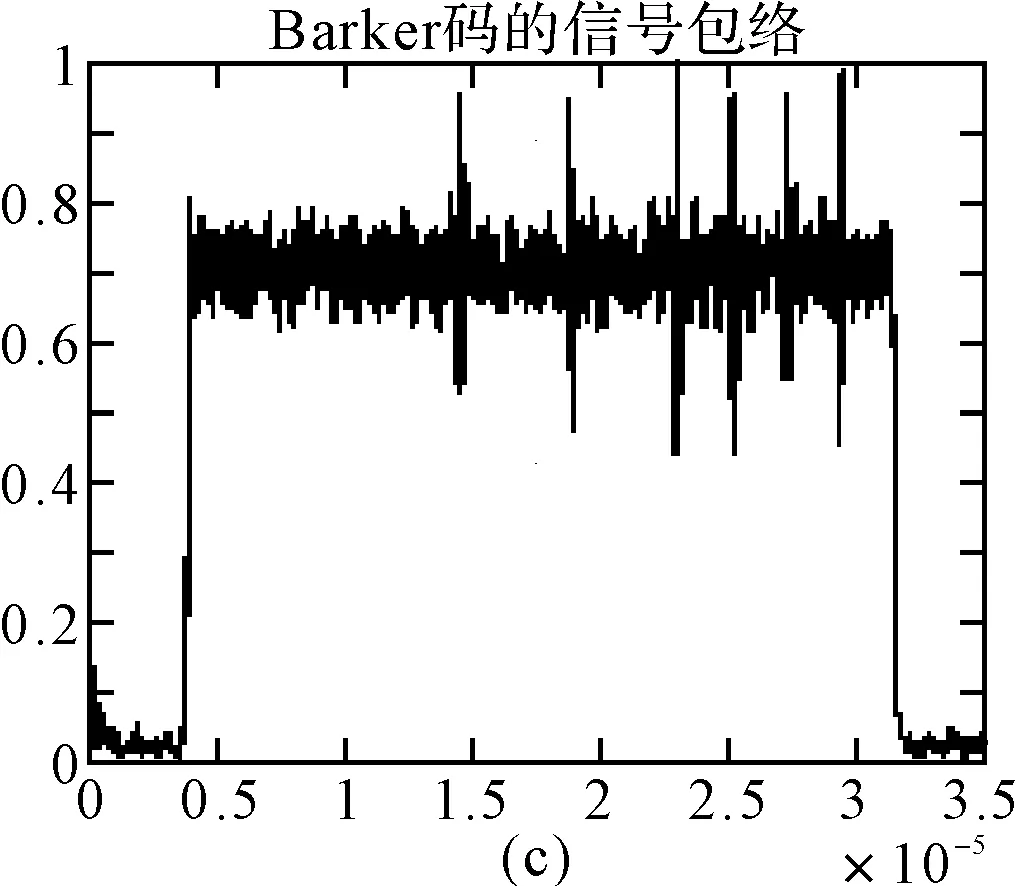


图4 实验信号的包络波形
直接利用Hilbert法提取的信号包络,得到的波形并不理想,给后续上升沿的提取和波形配对造成很大的误差影响。考虑到这个问题,为得到可靠的、更合乎实际的包络曲线,必须对初步提取的信号包络进行曲线拟合,本文选择三次样条插值法[11]对包络进行拟合,得到的结果如图5所示。


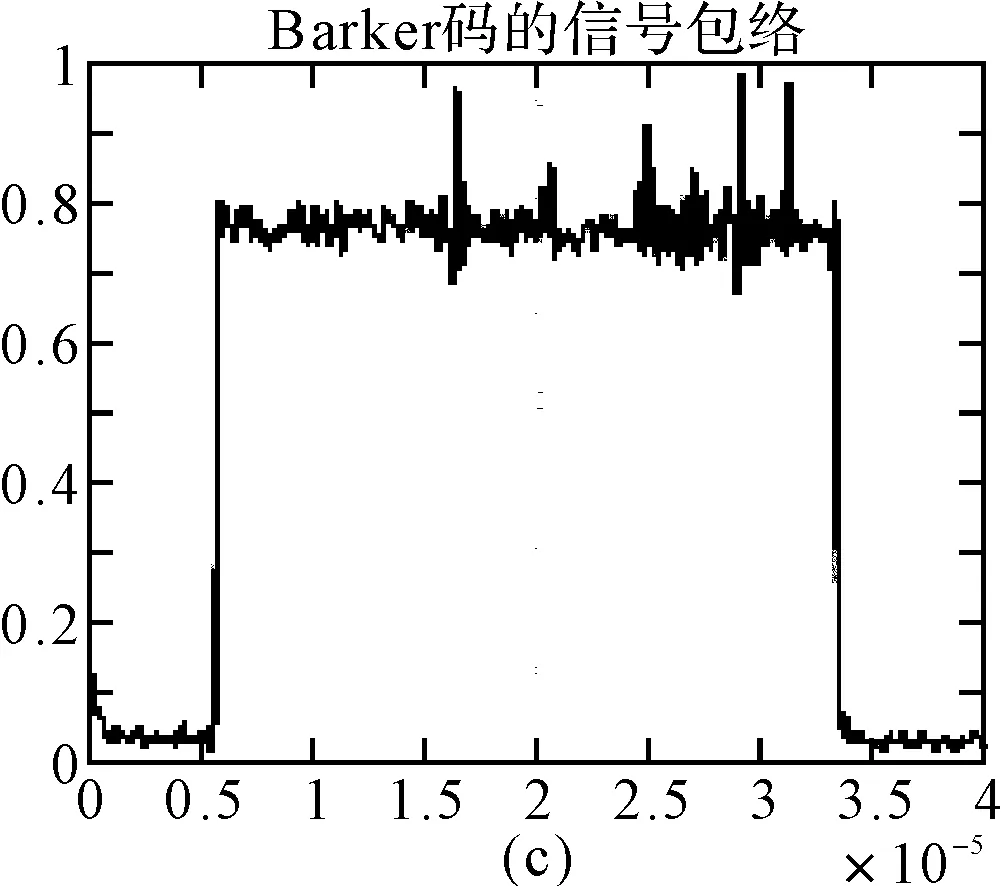


图5 拟合后的信号包络波形
3.2 脉冲上升沿的提取
对通过Hilbert法提取和三次样条插值法拟合的包络提取其前半部部分的波形,如图6所示。

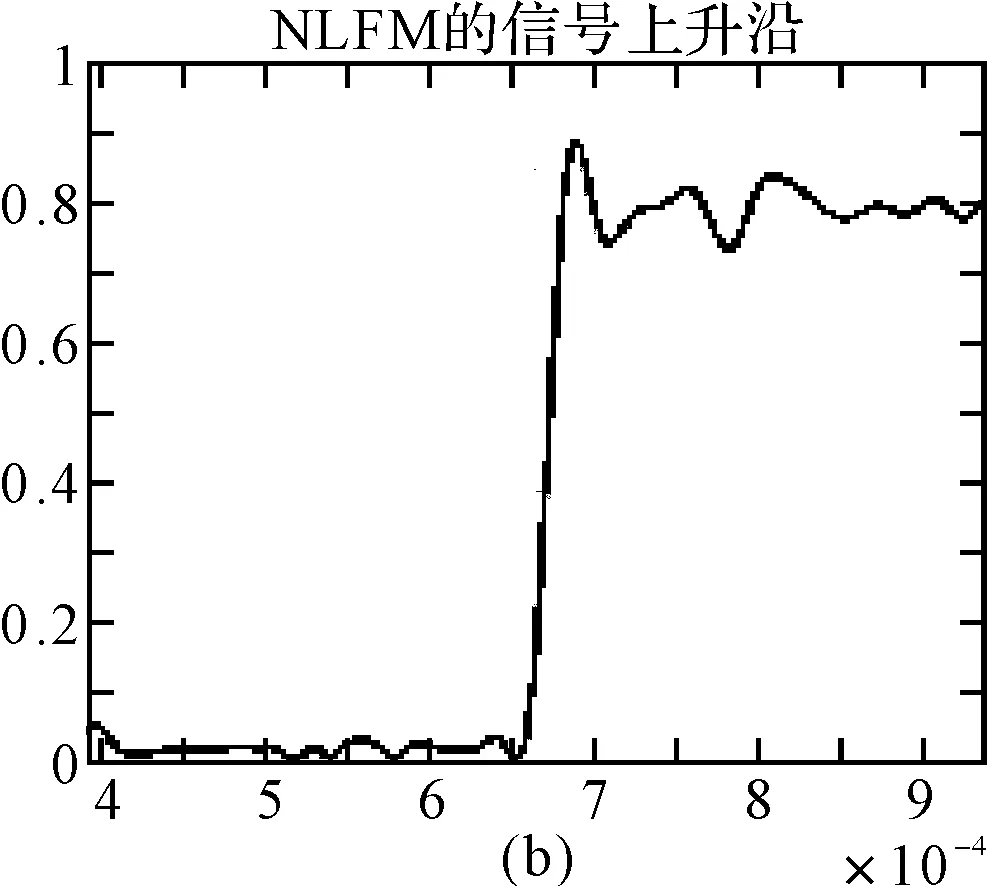
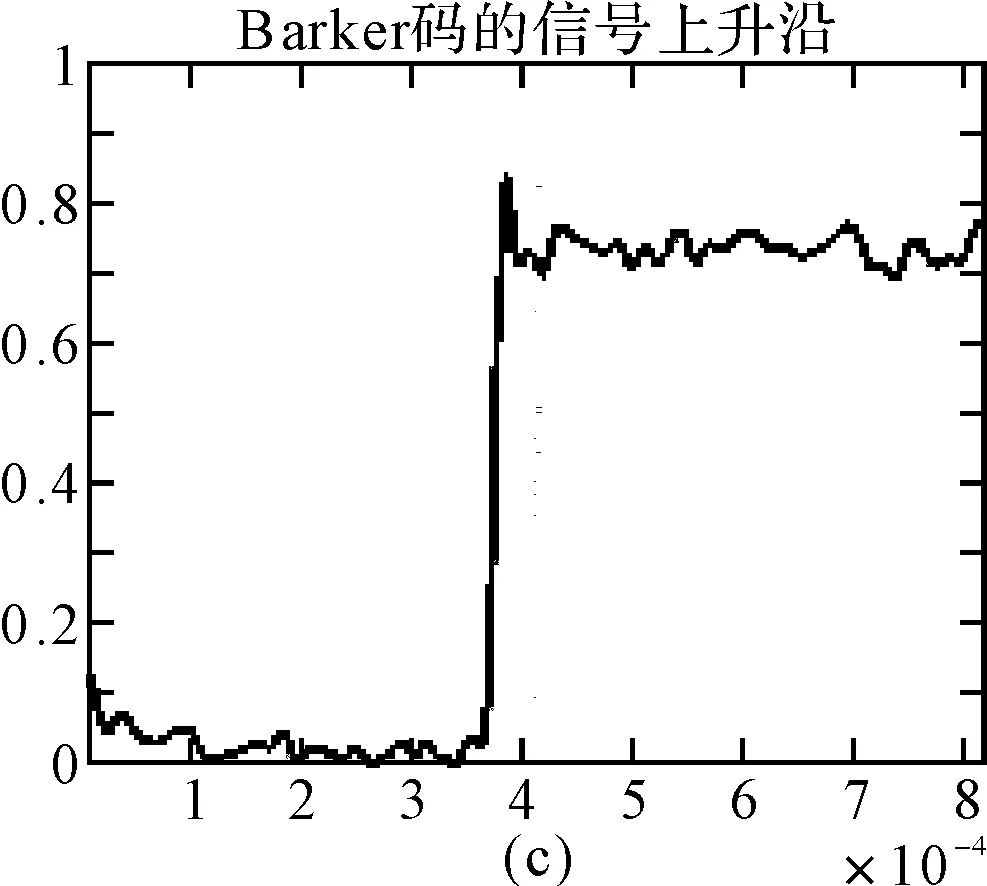


图6 包络前半部分波形
理论上,通常定义上升沿波形为包络幅度从10%到90%的部分,为了进一步验证上升沿作为指纹特征的有效性,又分别提取包络幅度的15%~85%,20%~80%,25%~75%,30%~70%作为上升沿波形,如图7~11所示。
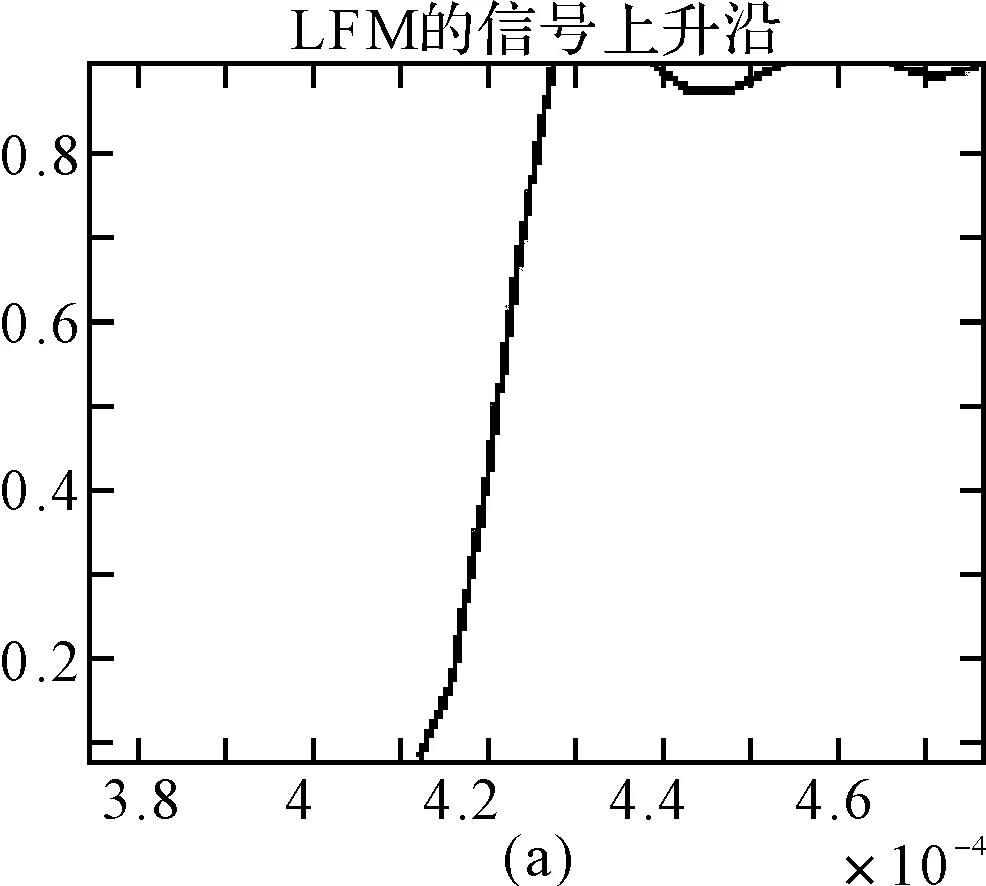


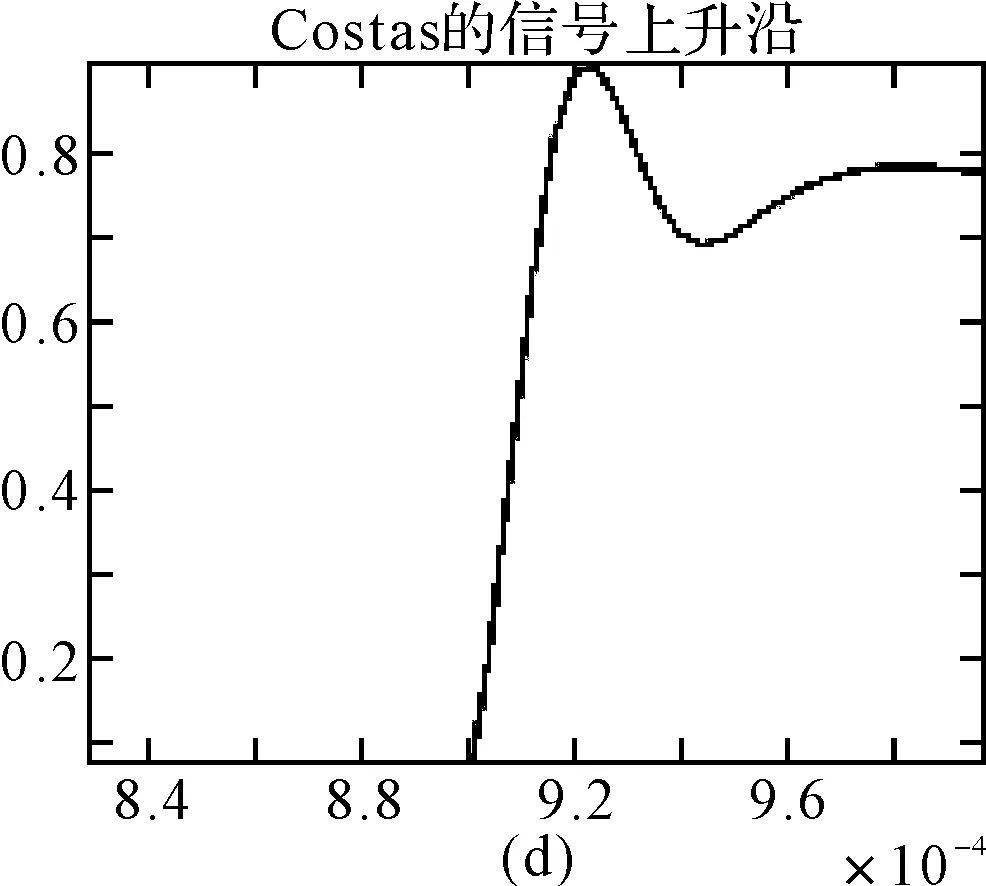

图7 10%~90%的上升沿波形
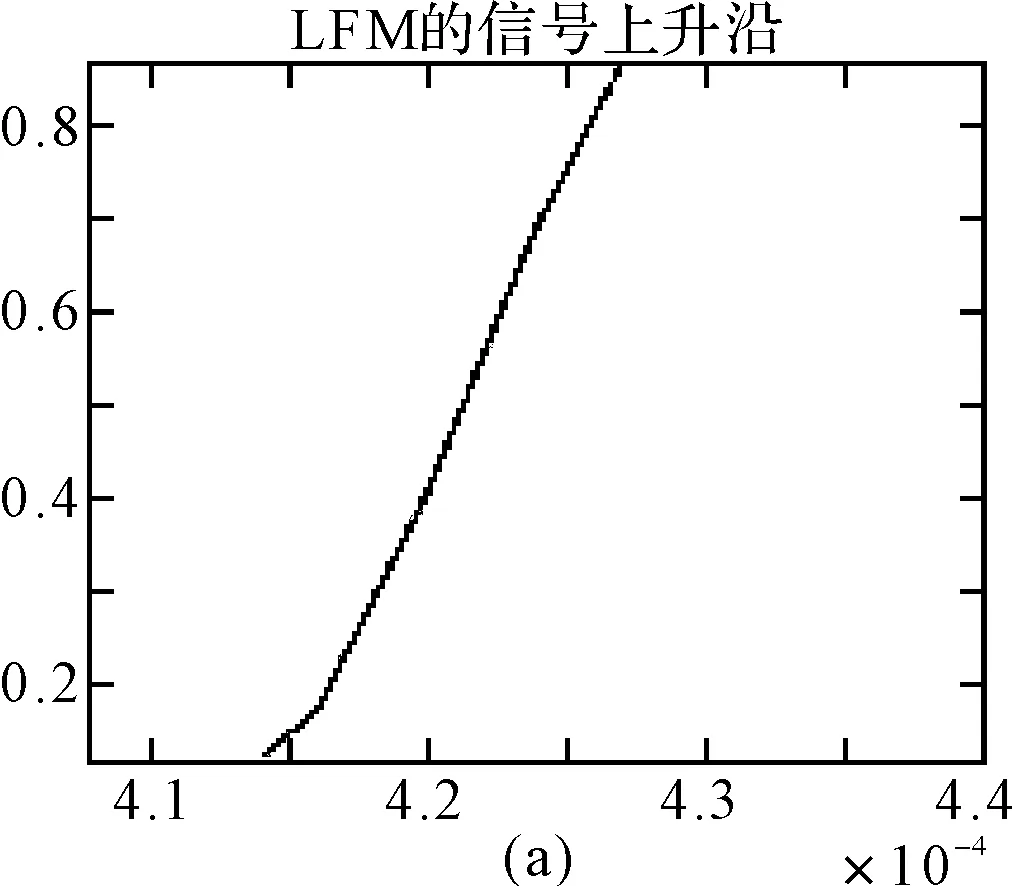
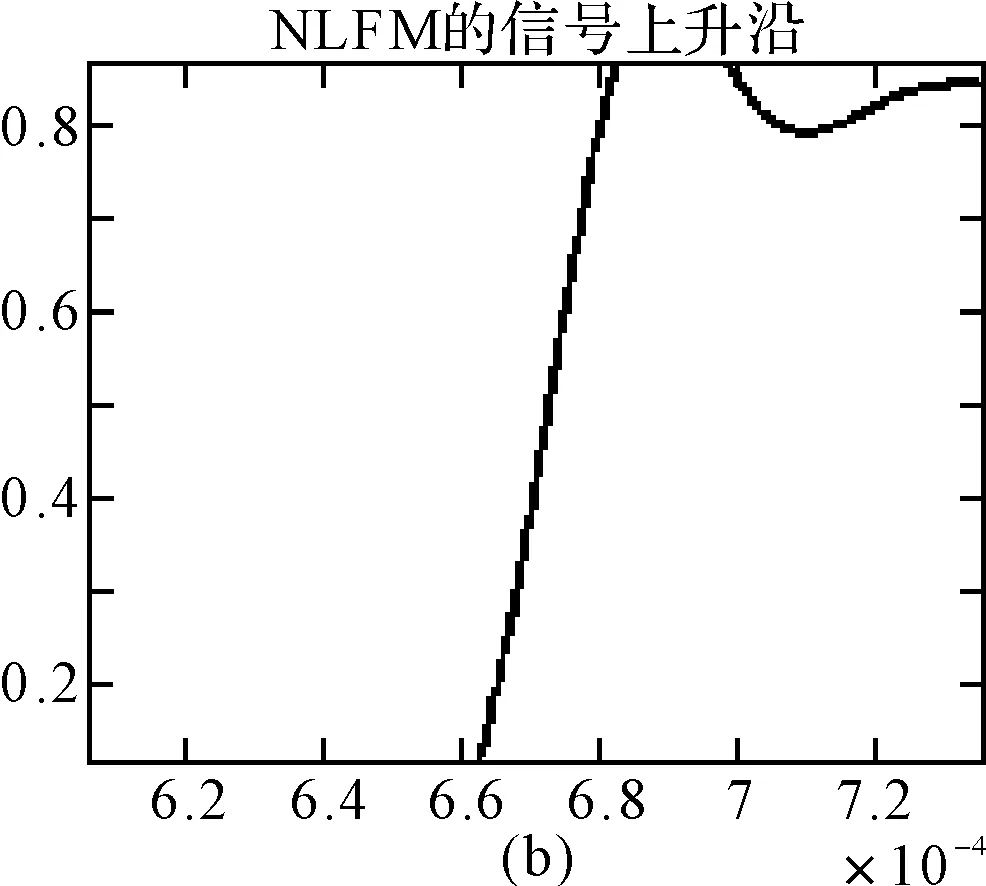

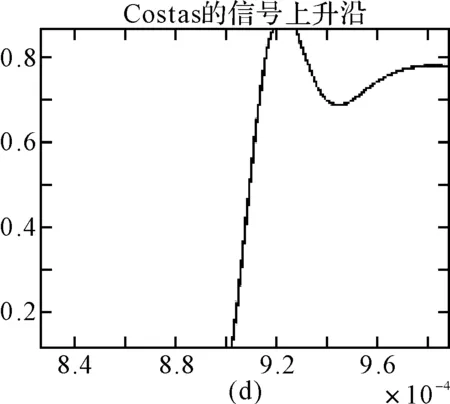

图8 15%~85%的上升沿波形

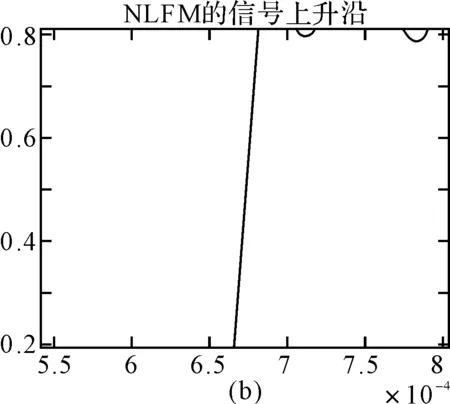



图9 20%~80%的上升沿波形




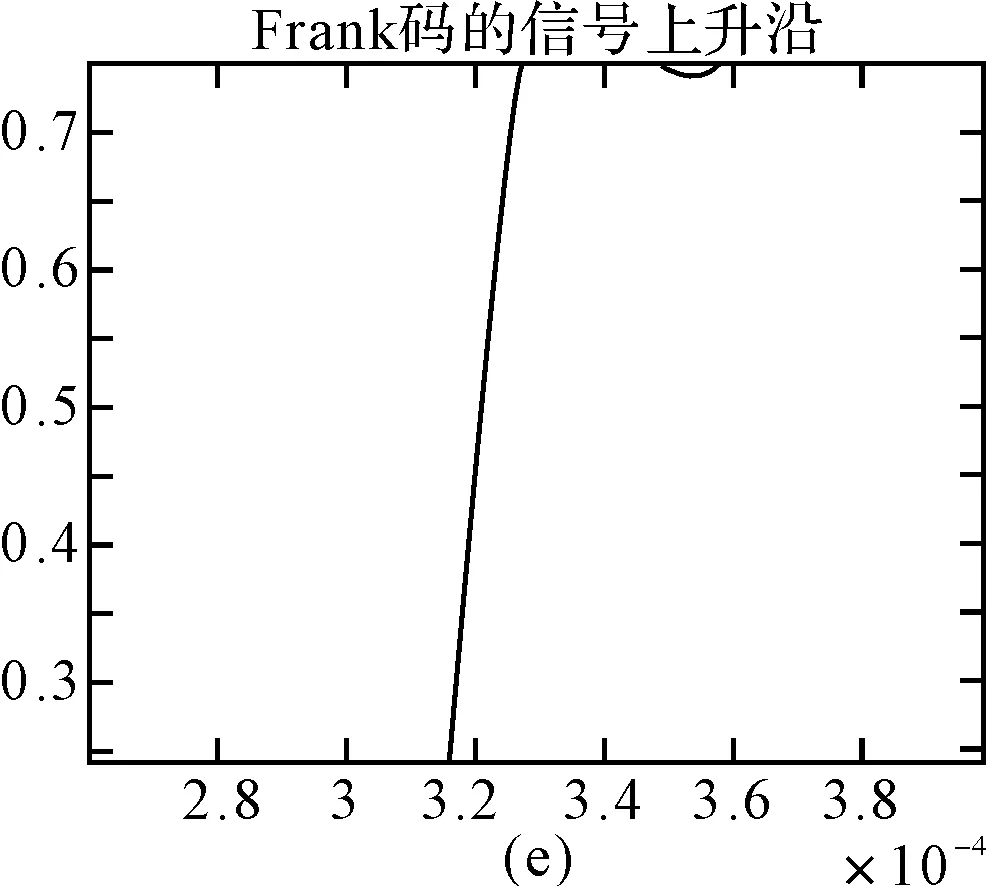
图10 25%~75%的上升沿波形

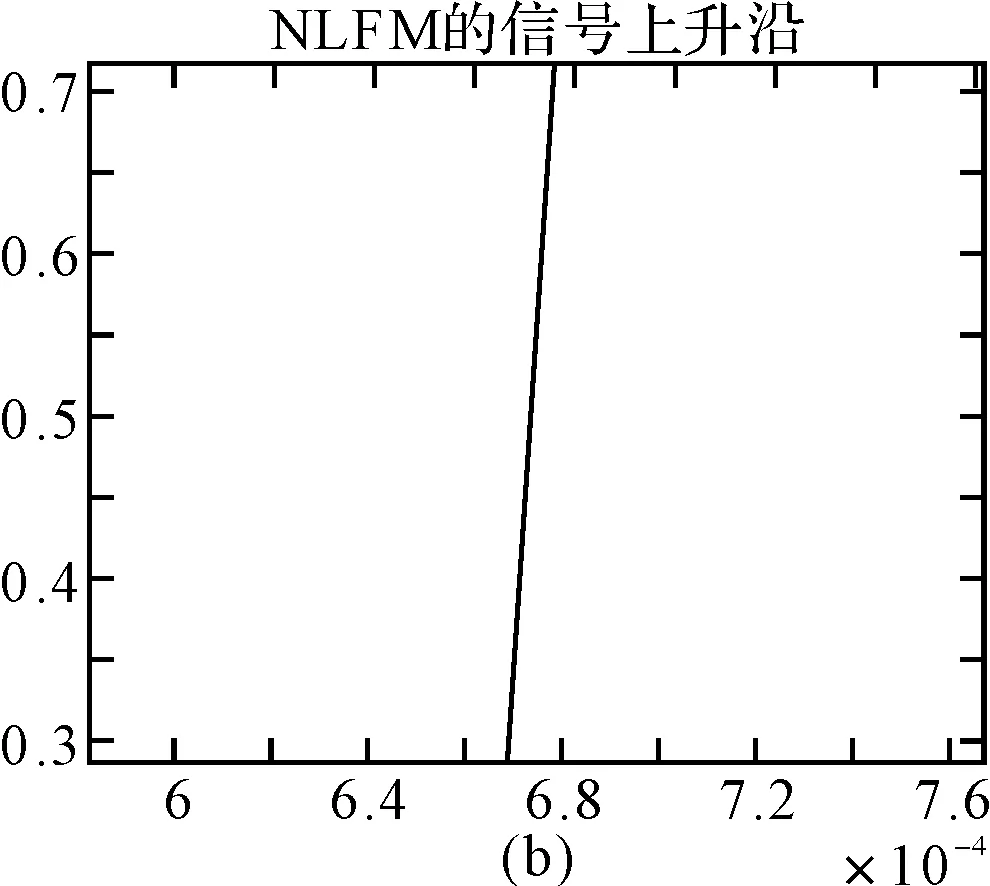


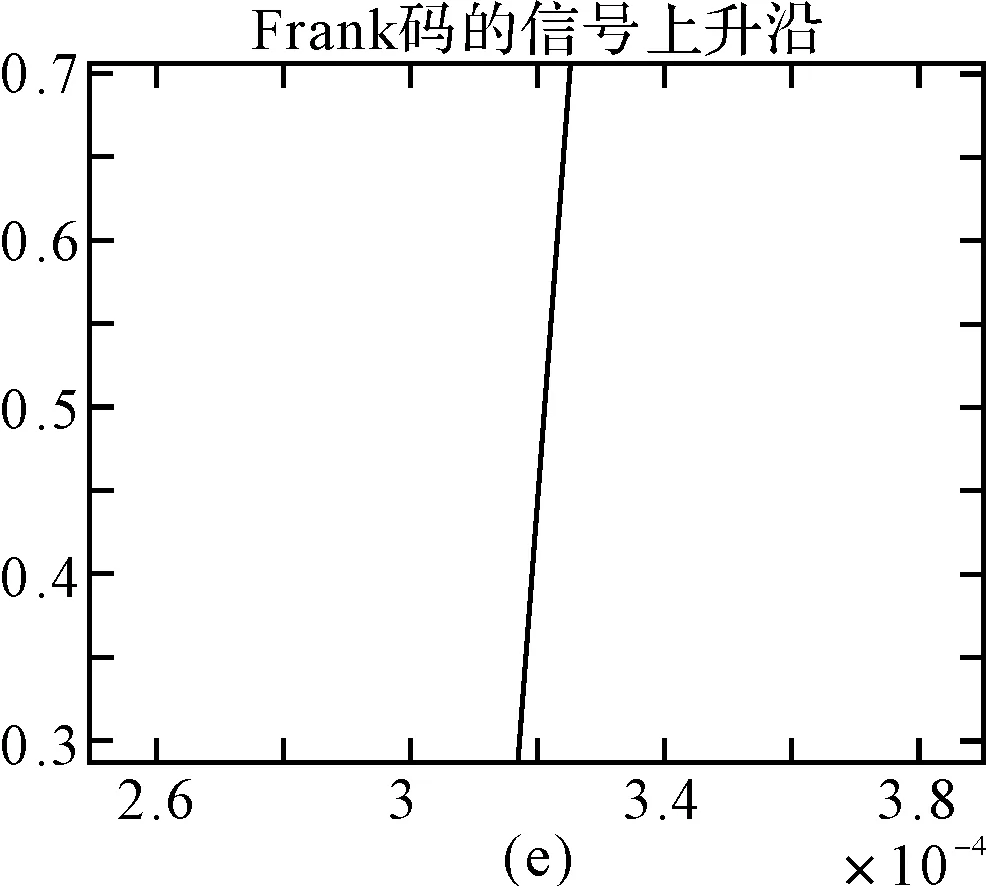
图11 30%~70%的上升沿波形
对于任意两个波形来说,其在几何角度的相似度越高,则两个波形越相关,所以任一信号脉冲包络上升沿波形与某一信号“标准”脉冲包络上升沿波形模板的相似度可以通过某种相似性度量的方法求得。而波形配对需要在相同采样率和理想接收机带宽的条件下,并完成归一化,波形对齐等预处理之后进行。
4 基于上升沿波形配对的信号分选
对于任意两组上升沿波形,其波形的匹配度越高,则说明两段上升沿波形越相似,也即可以判断两波形是来自同一辐射源个体的信号,实现脉冲配对。关于相似性度量的方法,本文采用Hausdorff距离法来计算上升沿波形之间的相似度。
4.1 Hausdorff距离法
Huasdorff是一类定义为两个点集之间的max-min型距离函数[12],它主要用于计算两个点集之间的相似程度,且无需考虑两个点集中的点是否存在某种对应关系,因而可以在没有映射关系的前提下计算两个点集之间的相似程度。
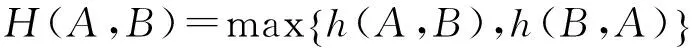
(3)

4.2 仿真实验
由Hausdorff距离函数的定义可知,在仿真实验中,取第一个信号包络的上升沿作为模板波形A,将随后的脉冲包络上升沿看作待配对波形集B,通过计算模板波形A与待配对波形集B中每个样本的Hausdorff距离值并比较,对大量的实验数据进行分析,判断待配对波形集B中的样本与模板波形A是否归属同一辐射源,并通过聚类法实现信号的分选。算法流程图如图12所示。

图12 基于上升沿波形配对分选方法的流程图
在波形配对的思想中,上升沿波形和采样点数(这里的采样点数指的是单个完整包络所有点的个数,下同)的选择对分选方法结果的影响很大,下面做了三组实验。
实验一:验证上升沿波形的指纹特性
实验样本来自三个不同辐射源,其中雷达发射机为辐射源1,Agilent E4438C信号源为辐射源2,某模拟雷达样机为辐射源3。发射类型、参数相近的信号,每个辐射源信号截取10个脉冲,以信号包络幅值从10%~90%的上升沿波形为模板波形A1、A2、A3,待配对波形分别为B1、B2、B3,分别与模板波形A1进行Hausdorff距离的运算,在相同采样的前提下,归一化后结果如表2所示。

表2 10%~90%上升沿的Hausdorff距离值(辐射源1)
通过对比表2中的Hausdorff距离值,发现待配对波形集B1与模板波形A1的Hausdorff距离普遍最小,说明匹配度最高,模板波形A1与B1中的脉冲信号来自同一个辐射源,从而实现脉冲配对。为了进一步验证,再分别计算待配对波形B1、B2、B3与模板波形A2、A3的Hausdorff距离,相同采样下,归一化后结果如表3、表4所示。

表3 10%~90%上升沿的Hausdorff距离值(辐射源2)

表4 10%~90%上升沿的Hausdorff距离值(辐射源3)
比较表3、表4的数据可知,A2与B2,A3与B3中的波形之间的Hausdorff距离值相对最小,匹配度最高,可以判断A2与B2,A3与B3分别归属同一辐射源。证明了上升沿波形具有指纹特性。
因此,可以对每个辐射源提取一个脉冲包络的上升沿作为模板波形,与待配对波形进行Hausdorff距离的计算,对得到的Hausdorff距离值进行聚类分析,完成信号分选。利用三个辐射源发射类型、参数相近的信号,采集1000个脉冲,在采样点数为10000,信噪比为10dB的条件下,基于上升沿波形的分选正确率到达96.76%,验证了上升沿波形作为个体特征用于信号分选的有效性。
实验二:上升沿波形的选择对分选的影响
已经验证了上升沿波形的指纹特性,下面探究上升沿波形的选择对分选结果的影响。仍以实验一中LFM信号的上升沿为模板波形A,其中A1、A2、A3、A4、A5分别代表幅值10%~90%、15%~85%、20%~80%、25%~75%、30%~70%的上升沿波形。而NLFM、Barker码、Costas、Frank码信号的上升沿归属待配对波形集B。其中B1j、B2j、B3j、B4j分别为NLFM、Barker码、Costas、Frank码信号,j=1,2,3,4,5分别表示幅值10%~90%、15%~85%、20%~80%、25%~75%、30%~70%的上升沿波形,采样点数为10000,归一化后计算波形之间的Hausdorff距离,结果如表5所示。

表5 不同上升沿之间的Hausdorff距离值
通过观察表5中数据发现:不同信号样式提取相同段的上升沿波形都相对收敛,且幅值跨度越小的上升沿波形收敛性也越好。为了进一步研究,仍然是同一辐射源,对LFM信号添加频率捷变特性,中心频率在固定范围内随机跳变,截取10个脉冲提取上升沿波形,其中第一个脉冲的上升沿作为模板波形A,剩下9个脉冲为待配对波形为B1∽B9,采样点数为10000,计算Hausdorff距离,结果如表6所示。
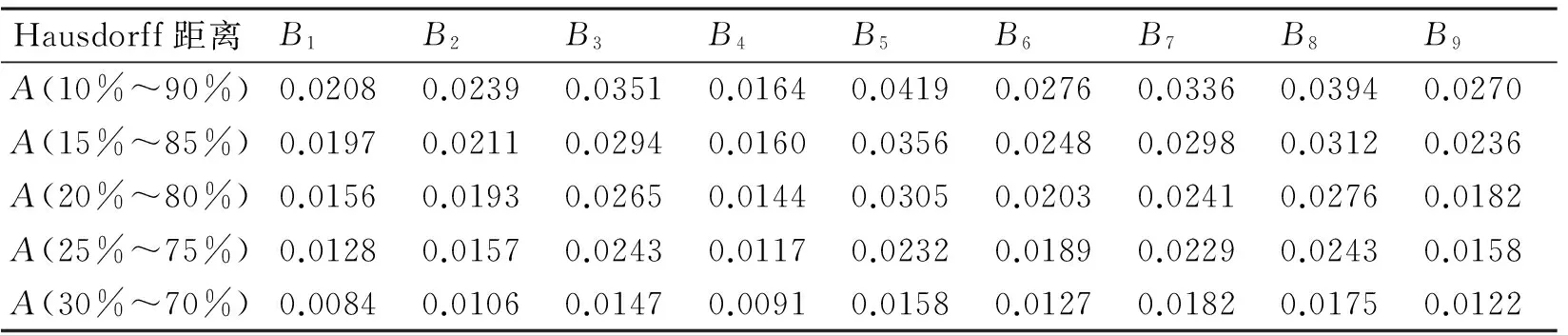
表6 模板波形A与待配对波形B的Hausdorff距离值
观察结果可得:频率捷变的LFM信号上升沿依然具有收敛性,且幅值跨度越小的上升沿波形收敛性也越好。可以初步得出结论:由于提取的上升沿波形的幅值跨度减小,受噪声干扰的影响越小,且波形缩短导致参与计算的点数减少,收敛性自然越好。那么,为了验证上升沿波形选择对分选结果影响,是否收敛性越好就分选正确率就越高,利用实验一中三台不同的辐射源发射信号,采集大量1000个脉冲(此处不考虑脉冲重叠的情况)进行上升沿的波形配对,确保接收机带宽足够,采样率相同且噪声环境相同(信噪比为10dB),得到实验结果如表7所示。
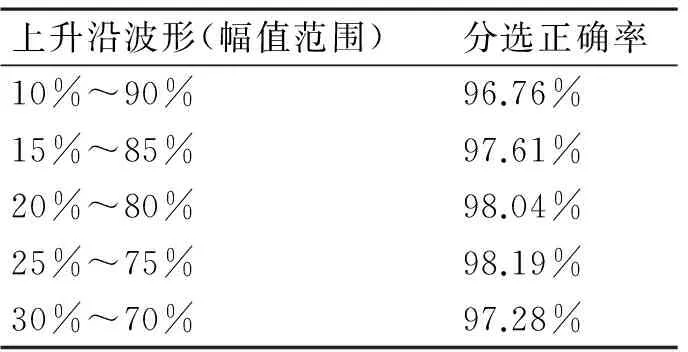
表7 不同上升沿波形的实验结果
由表7可知:幅值跨度的减小与分选正确率的提高并不成正比,因为参与计算的点数过少,求得的Hausdorff距离值不准影响聚类分析的效果,容易造成误匹配,从而影响了分选的结果,幅值从25%~75%的上升沿波形具有最高的分选正确率。即该段上升沿波形具有最好的指纹特性,在减小运算量的情况下,得到最高的分选正确率,提高了分选的效率。
实验三:采样点数对分选的影响
已经证明了选择幅值从25%~75%的上升沿波形具有最高的分选正确率,继续研究采样点数的选择对分选结果的影响,我们知道相同的两段波形,采样点数不同,其相似性度量的结果是不同的,进而影响到分选的结果。且由于采样点数与Hausdorff距离的计算量正相关,所以这里需要考虑运算时间的问题,探究采样点数与分选正确率、计算时间之间的关系。
仍然用实验一中的三个辐射源发射发射类型、参数相近的信号,采集1000个脉冲,信噪比为10dB,提取信号包络幅值从25%~75%的上升沿波形进行配对分选,方法同上,采样点数分别为5000、10000、20000、40000,所采用计算机的处理器为英特尔第四代酷睿 i5-4200H 2.8GHz 双核,内存:8G,64位操作系统。使用Matlab中的tic toc函数,得到如表8所示的结果。

表8 不同采样点数的实验结果
根据表8中的结果可以发现,采样点数的增加有利于分选正确率的提高,因为同一段波形,采样点数越多,对波形的描述就越详细、越准确,配对求得的Hausdorff距离和聚类的结果也越精确,从而提高了分选的正确率,但随之也带来运算量增大的问题。可见,提高正确率是以牺牲实时性为代价的,根据实际情况的要求,在保证一定分选正确率的前提下,采样点数的选择不是越高越好,还需要考虑运算效率的问题。
5 结语
本文通过理论分析、实际数据的实验,验证了信号包络上升沿波形的指纹特性,并利用Hausdorff距离函数计算相似度,采用波形配对的方法进行信号分选。通过三组实验的结果分析,可以得出结论:基于上升沿波形配对的分选方法能够有效的解决当前分选方法中普遍存在的增批、漏批问题,且上升沿波形和采样点数的选择对分选结果都有影响,符合波形相似性度量理论。此外分选正确率可能还跟噪声环境(信噪比),包络提取和拟合的方法,相似性度量的方法,分类的方法等有关,可进一步深入研究。
[1] 黎聪. 雷达的信号分选技术研究[D]. 成都:电子科技大学,2015.
[2] 秦长海,薛景. 基于脉冲上升沿的雷达个体识别方法[J]. 舰船电子对抗,2009,111(06):12-18.
[3] 王宏伟,赵国庆,王玉军. 基于脉冲包络前沿波形的雷达辐射源个体识别[J]. 航天电子对抗,2009,25(02):35-38.
[4] Tao-wei C, Wei-dong J, Jie L. Feature Extraction Using Surrounding-line Integral Bispectrum for Radar Emitter Signal[C]// IEEE International Joint Conference on Neural Networks, 2008.IJCNN 2008. (IEEE World Congress on Computational Intelligence).2008:294-298.
[5] 张国柱,黄可生,姜文利等. 基于信号包络的辐射源细微特征提取方法[J]. 系统工程与电子技术,2006,28(6):741-742.
[6] 刘爱霞,赵国庆. 雷达信号包络特征的检测与分析[J]. 电子对抗技术, 2002, 17(3): 12-16.
[7] 林震鹊,姜秋喜,黄建冲. 雷达脉冲信号上升_下降沿测量影响因素[J]. 四川兵工学报, 2010, 31(1):117-120.
[8] 秦长海,薛景. 基于脉冲上升沿的雷达个体识别方法[J]. 舰船电子对抗, 2009, 32(6): 27-30.
[9] 辛永升,陈玮敏. 发射机调制器脉冲波形问题探讨[J]. 现代雷达, 2002, 24(3): 65-67.
[10] Hahnsl. Hilbert Transforms in Signal Processing[M]. Boston: Artech House, 1996:97-101.
[11] 樊天锁,芮兵. 样条插值的MATLAB实现[J]. 佳木斯大学学报(自然科学版), 2011, 29(2): 238-240.
[12] 曹京京. Hausdorff距离的计算原理及其在二维匹配中的应用[D]. 大连:大连理工大学,2013.
[13] 蒋鹏. 雷达信号细微特征分析与识别[D]. 哈尔滨:哈尔滨工程大学,2012.
Signal Sorting Method Based on Rising Edge Waveform Matching
WU Weicheng1PAN Jifei1LIU Xin2
Aiming at the problem of increasing batch and missing batch in current sorting algorithm, a method based on the matching of rising edge waveform is proposed. By using the method of Hilbert extraction waveform in the envelope of the signal source, radiation, and fitted by cubic spline interpolation method, the method extracts fingerprint characteristics of envelope rise along the waveform characteristics, as the similarity measure method of waveform matching using Hausdorff distance function. Based on three sets of experiments, the effectiveness of the method is verified, and the influence of the selection of the rising edge and the sampling points on the method is verified.
signal sorting, pulse envelope, rising edge waveform, Hausdorff distance
2016年6月17日,
2016年7月21日
国防预研基金项目“基于脉冲流的雷达精确识别技术研究”(编号:41101020207)资助。
吴惟诚,男,硕士研究生,研究方向:雷达辐射源信号分选识别技术。潘继飞,男,博士,副教授,研究方向:雷达对抗。刘鑫,男,博士,博士后,研究方向:雷达对抗。
TN974
10.3969/j.issn.1672-9730.2016.12.021
