引入外速度的激光陀螺罗经水平对准方法*
2017-01-11路君里辛月宽靳碧耀
张 健 路君里 辛月宽 靳碧耀
(中船航海科技有限责任公司 北京 100070)
引入外速度的激光陀螺罗经水平对准方法*
张 健 路君里 辛月宽 靳碧耀
(中船航海科技有限责任公司 北京 100070)
激光陀螺罗经作为一种价格相对低廉、精度适中的导航设备,必将在导航领域受到广泛的重视。文中针对激光陀螺罗经研制与实现关键技术之一水平通道控制技术进行了研究与验证。分析验证了现阶段水平通道控制技术中存在的问题,提出引入外速度补偿的水平对准方法,实现机动环境下的水平对准。
激光陀螺; 平台罗经; 水平对准; 水平阻尼
(CSSC Marine Technology Co., Ltd, Beijing 100070)
Class Number U666.151
1 引言
激光陀螺罗经是一种精密而又复杂的导航仪器,能够连续提供舰船等运载体的航向及横纵摇信息,进而为舰船上的武备、控制等系统提供精确的基准信息[1~2]。相比较于舰船上高精度的主惯性导航设备,激光陀螺罗经虽是配设备,但可以很好地满足各系统需求,而且价格相对较低,其在舰船上的作用是不可替代的。所以一直以来激光陀螺罗经的发展深受各国家青睐[3]。
本文研究分析了传统罗经系统的水平对准方法,针对现存水平对准过程受舰船机动航行及舰船摇摆影响,提出了引入外速的水平对准方法。实现机动环境下的水平对准。
2 二节水平对准方法的研究
激光陀螺罗经属于捷联式平台罗经,其姿态矩阵代替实体平台,起到惯性器件量测基准的作用。在系统工作之前,必须进行初始对准以保证系统精度。初始对准过程一般可分为水平对准和方位对准两步,水平对准是方位对准的基础,因此,水平对准研究的意义十分重大[4]。
传统罗经系统的二阶水平对准回路原理如图1、图2所示,东向和北向的水平对准回路类似,在两个回路中加入的阻尼环节相同。以北向水平回路为例,▽x表示加速度计的零位误差;adx表示加速度计测量到干扰加速度;εy表示陀螺的常值漂移;▽εy表示陀螺仪测量到的干扰信息;ωcx表示控制角速度;φx表示水平北向误差角;k1和k2表示二阶水平对准回路中的参数[5]。
图1、图2所示的水平对准回路特征方程为
(1)
式(1)表明,该系统是一个二阶系统,标准二阶系统的特征方程如式(2)所示:
s2+2ξωns+ωn2=0
(2)
对比式(1)与式(2)两个特征方程,可以得到罗经二阶水平对准回路的参数k1和k2。
(3)
式中,ξ表示阻尼系数,ωn表示没有阻尼情况下的自然频率。
假设水平对准的调节时间为60秒,选取误差带Δ=0.05,由二阶系统动态性能指标可知调整时间为
(4)
实际应用中,常取
(5)
(6)
3 引入外速度补偿的二节水平对准方法
二阶水平对准的实质是在系统中加入阻尼环节,使导航误差中的舒勒震荡分量衰减下来,以达到快速水平对准的目的。但与此同时舒勒调谐条件被破坏,水平对准过程中会受到加速度干扰,影响水平对准[6]。为了克服该影响,在二阶水平对准过程中引入外速度信息,对载体加速度引起的对准误差进行补偿,以达到较高的水平对准精度。
3.1 载体加速度对水平对准的影响
以系统北向水平对准通道为例,假设将通道中加入的阻尼环节等效为Hy(s),则北向水平通道的等效图如图3所示。
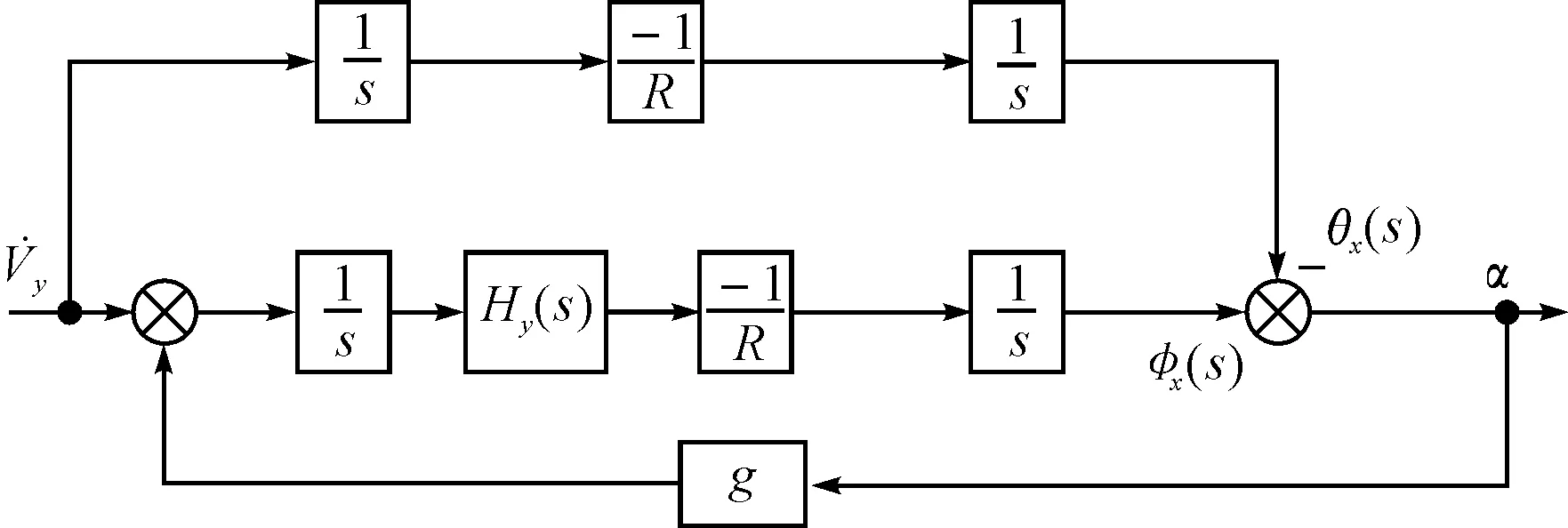
图3 水平对准北向通道方块图
为适当简化分析过程,图3中只考虑载体加速度的作用,未考虑加速度计误差ΔAy,等效陀螺漂移误差εx,初始误差角α0等误差源,假设这些误差源为0。
图3中θx(s)是地理坐标系在惯性空间转动的角度;φx(s)是姿态矩阵解算出的数学平台在惯性空间转动的角度。则水平倾角α为
α(s)=φx(s)-θx(s)
(7)
其中:
(8)
将式(8)代入式(7),整理得:
(9)

一般情况下,对于惯导解算过程,舰船运动加速度并不算太大,其带来的误差不是很大,而且由于阻尼的作用,一次加速度或者速度干扰产生的误差将在一到两个舒勒周期后消失。但一个舒勒周期长达84.4min,而且一般载体在一个周期这么长的时间段内,其机动是经常性的,更严重的是这种干扰所产生的误差角可能是累积的。对于水平对准过程,对准时间短、对准精度高是其最终目标,因此降低载体加速度及速度对水平对准误差角的影响是极为必要的。
3.2 引入外速度的水平对准分析
如果在运载体上有测量外部速度的设备,而且测量精度较高,比如电磁计程仪、多普勒计程仪等,则可以将测得的外速度信息引入水平对准过程中,实现有外速度补偿的水平对准[7]。下面从理论上根本的分析有外速度补偿时,载体加速度及速度对水平误差角的影响。
以北向水平对准通道为例来说明引入外速度补偿的水平对准问题。图4所示为北向水平对准通道方块图,图中通过阻尼网络[1-Hy(s)]将外测速度引入到系统中。

图4 北向水平对准通道方块图
图中外测速度信息Vry是真实速度Vy与外速度误差δVry之和。
从图4可知:
α(s)=φx(s)+Lx(s)-θx(s)
(10)
其中:
(11)
Vry(s)=Vy(s)+δVry(s)
(12)
将式(11)、(12)代入式(10),并整理得:
(13)

从物理意义上讲,引入外速度到水平对准网络,并不能起到阻尼的作用,而是给在系统中加入了一条补偿通道,补偿掉由于加速度引入而带入系统的干扰误差。虽然这一过程又给系统带来了新的外速度误差δVry(s),但外速度误差δVry(s)相比于运载体的速度Vy要小得多,通过对比式(9)与式(13)可知,引入较高精度的外速度信息可以大大提高水平对准精度,而不再产生过大的动态误差。
进一步分析外速度误差对水平对准精度的影响。根据拉氏变换微分定理:
即:
(14)
将式(14)代入式(13)得:
(15)
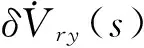
因此,采用引入外速度补偿的水平对准时,不一定要求连续提供外部速度信号,可以只在判明载体处于机动状态的情况下接入。而当载体作等速直线航行时且摇摆不明显的情况下,断开外速度信号,这样可以减少外速度误差变化率造成的误差。
4 实验仿真分析
为了验证水平对准受载体加速度的影响,以及当向系统引入外部速度信息时对该影响的补偿效果,本节设计了两组实验:第一组在不同载体加速度情况下进行水平对准,第二组在第一组的基础上进行外速度补偿,以验证外速度补偿效果。
4.1 实验仿真环境
为验证本章理论分析,分别以下两组实验环境下进行2分钟水平对准。
实验一:载体以[5m/s,5m/s,0m/s]的初始速度航行,在航行过程中分别以[-0.1m/s2,-0.1m/s2,0m/s2]和[-0.5m/s2,-0.5m/s2,0m/s2]的加速度做匀加速直线运动。
实验二:沿用实验一方案的载体机动条件,用加速度计算速度代替外速度引入到系统中,进行外速度补偿的水平对准实验。
舰船在海面上系泊或者航行,受海浪及风等自然条件的影响,不可避免的会产生摇摆加速度,对摇摆基座环境建模如下[10]。
当载体存在摇摆时,模型可以表示为
(16)
当载体存在纵荡、横荡、垂荡引起的线速度时,模型可以表示为
(17)
当载体存在高频振动引起的线速度时,模型可以表示为
(18)
上述各模型中参数的取值如表1所示。

表1 摇摆模型参数取值
惯性测量元件的相关误差参数见表2。

表2 惯性测量元件误差参数
水平对准的时间设置见表3。
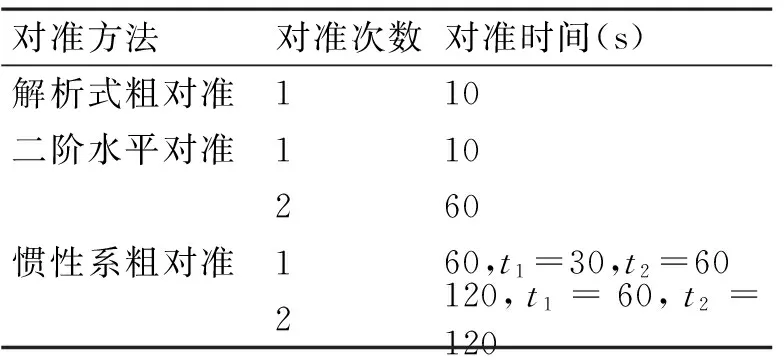
表3 水平对准时间
4.2 实验仿真结果
在实验一条件下分别进行50次水平对准仿真实验,加速度为[-0.1m/s2,-0.1m/s2,0m/s2]的水平对准结果图如图5所示,加速度为[-0.5m/s2,-0.5m/s2,0m/s2]的结果图如图6所示。

图5 50次较小加速度情况下二阶水平对准结果图
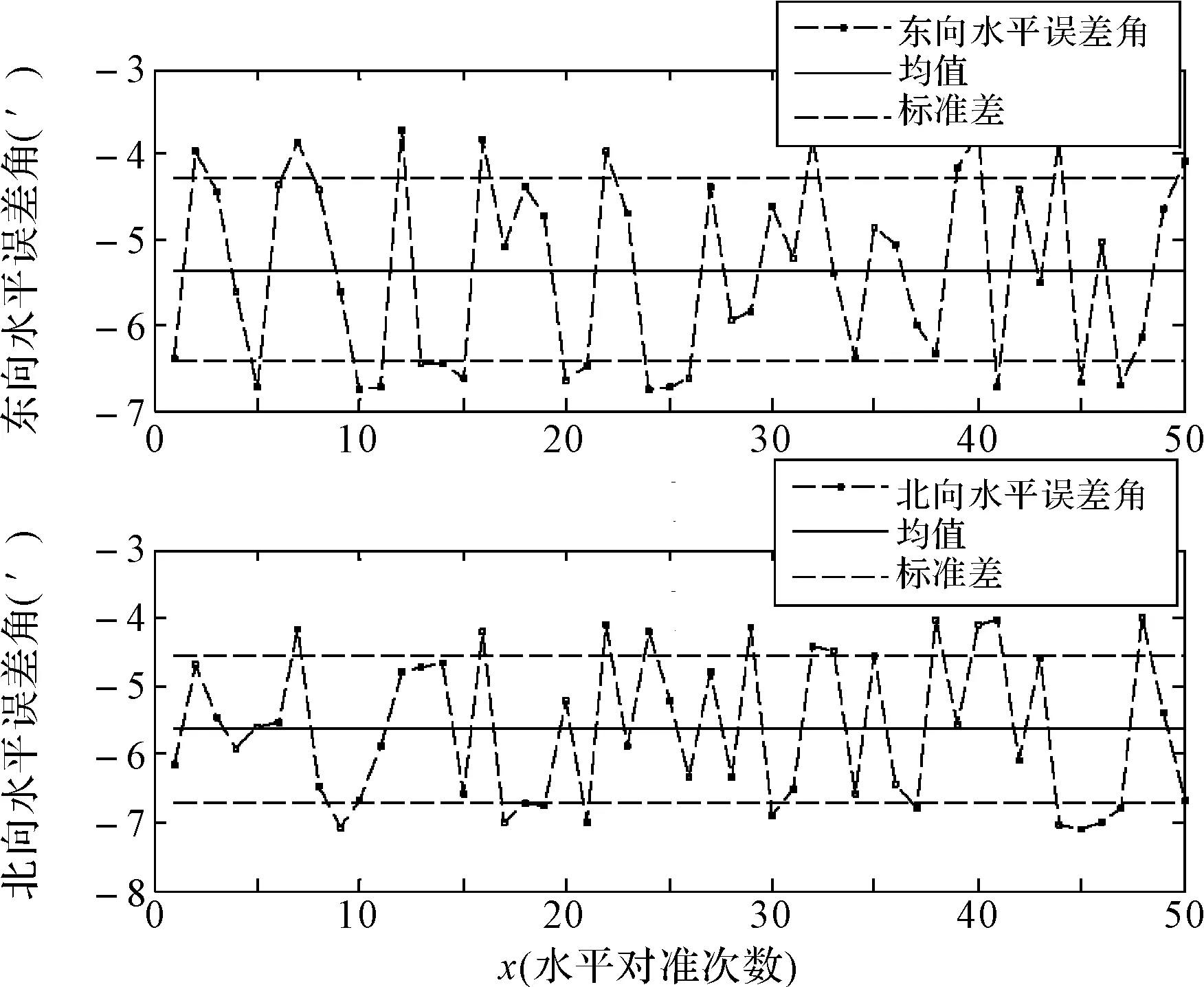
图6 50次较大加速度情况下二阶水平对准结果图
比较两结果图可知,两次实验结果均不能够满足水平对准要求,但较之图5的结果图6的对准结果更差一些,说明当载体加速度越大时其对水平对准的影响越大。
在实验二条件下分别进行50次水平对准仿真实验,经过外速度补偿后加速度为[-0.1m/s2,-0.1m/s2,0m/s2]的水平对准结果图如图7所示,经过外速度补偿后加速度为[-0.5m/s2,-0.5m/s2,0m/s2]的结果图如图8所示。

图7 50次外速度补偿后较小加速度情况下二阶水平对准结果图

图8 50次外速度补偿后较大加速度情况下二阶水平对准结果图
从图7与图8可以很直观的看出,经过外速度补偿后两种机动条件下的水平对准结果均有了很大的改善。两次实验50次外速度补偿后的水平对准结果均值及标准差见表4。

表4 补偿前后水平误差角均值及标准差对比
从表4可知,在实验一中,两种加速度条件下的机动运动均使水平对准精度不能满足要求,而且加速度为[-0.5m/s2,-0.5m/s2,0m/s2]的水平误差角的均值与标准差都要比加速度为[-0.1m/s2,-0.1m/s2,0m/s2]的稍大,机动运动本身影响了敏感器件对地球自转及重力加速度的敏感,同时也加剧了摇摆运动对水平对准的影响,因此在两种加速运动情况下都无法满足对准要求。在实验二中,向系统中引入了外速度信息,可以看到两种加速度条件下的水平对准均已有了很大的改善,水平误差角均值都在1′以内,水平误差角标准差均在0.1′以内。外速度信息的引入相当于在系统回路中加入了一条补偿通道,将加速度引入到系统中的干扰信息补偿掉,以提高水平对准精度。
5 结语
本文从原理上分析了载体加速度对二阶水平对准的影响,同时提出将外速度信息引入到二阶水平对准环路,以补偿载体加速度对水平对准的影响,并在理论上论证了该方法的可行性。同时应用Matlab模拟不同加速度的机动环境,在该环境下对引入加速度信息前后的水平对准进行仿真,实验结果验证了引入外速度补偿方法的可行性。引入外速度补偿水平对准方法的提出对提高舰船机动性有着极其重要的作用。
[1] 经张俊,程向红,王宇.捷联罗经的动基座自对准技术[J].中国惯性技术学报,2009(4):408-412,418.
[2] 龙林川.平台罗经技术的发展[J].航仪通讯,1994,3:44-48.
[3] 陆元九主编.惯性器件[M].北京:中国宇航出版社,1993:5-6.
[4] 孙枫,孙伟.基于单轴转动的捷联系统粗对准技术研究[J].系统工程与电子技术,2010(6):1272-1276.
[5] 吉翠萍,陈勇,雷宏杰等.激光陀螺捷联惯性导航系统误差分析及仿真计算[J].应用光学,2005(3):5-8.
[6] 秦永元,朱新颖,赵长山等.舰载机捷联惯导自对准方案设计与仿真[J].中国惯性技术学报,2008(1):28-33.
[7] Titterton, D. H., Weston, J. L. Strapdown Inertial Navigation Technology[M]. 2nd ed.; IET, London, UK and AIAA, Virginia, USA.:2004.89-90.
[8] 魏国,刘灿,尹洪亮等.二频机抖激光陀螺单轴旋转惯导系统阻尼技术研究[J].导航与控制,2013(3):31-35.
[9] D.H. Titterton, J.L. Weston. Strapdown Inertial Navigation Technology Second Edition[M]. Lexington, Massachusetts: MIT Lincoln Laboratory,2004.56-57.
[10] 万德钧,房建成.惯性导航初始对准[M].南京:东南大学出版社.1998:113-115.
Horizon Alignment Method Introducing External Velocity for Laser Gyro Compass
ZHANG Jian LU Junli XIN Yuekuan JIN Biyao
Laser gyro compass as a relatively inexpensive, moderate precision navigation equipment, receives considerable attention in the field of navigation. The research and verification on horizon channel control technology which was one of the key technologies for development and realization of laser gyro compass had been done in this paper. The research started from the traditional horizon alignment and found some disadvantages of horizon control technology at present. In order to overcome the influence of maneuvering motion on the horizon alignment and the influence of swing acceleration on the horizontal alignment, the horizon alignment methods were proposed, in which external velocity was introduced for compensation.
laser gyro, platform compass, horizon alignment, horizontal damping network
2016年6月7日,
2016年7月26日
张健,男,工程师,研究方向:惯性导航,卫星导航。路君里,男,高级工程师,研究方向:卫星导航,惯性导航。辛月宽,男,工程师,研究方向:惯性导航,卫星导航。靳碧耀,男,工程师,研究方向:惯性导航,卫星导航。
U666.151
10.3969/j.issn.1672-9730.2016.12.015
