运用拓展的三波法求3+1维potential Yu-Toda-Sasa-Fukuyama方程的扭结呼吸波解

江建明

（百色学院 数学与统计学院，广西 百色 533000）

运用拓展的三波法求3+1维potential Yu-Toda-Sasa-Fukuyama方程的扭结呼吸波解

江建明

（百色学院 数学与统计学院，广西 百色 533000）

本文采用拓展的三波法，利用Darvishi的思想将不可积的方程化为Hirota的双线型式，利用Maple软件进行求解，得到了3+1维potentialYu-Toda-Sasa-Fukuyama方程的扭结周期双孤子解.

拓展的三波法；Maple软件；扭结周期双孤子解

1 拓展的三波法

对于一个给定的非线性偏微分方程[1],有如下形式:

步骤1：通过潘勒卫分析,根据变换

步骤2：把(2)代入(1)转化为双线性形式:

这里的D1,D2等为双线性算子的组合.定义为[2]

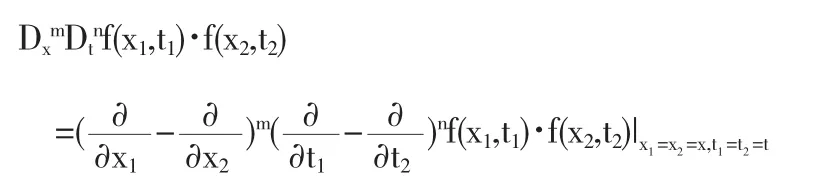
步骤3：对双线性形式再作变换，如作变换[3,4,5,6,]

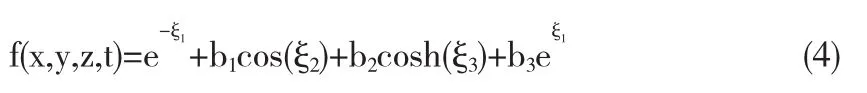
步骤4：把(4)代入(3),化简合并同类项之后,分别令e-ξ1, eξ1,cos(ξ2),sin(ξ2)，sinh(ξ3)，cosh(ξ3)等的系数为零, 可以得到一组关于上述参数的非线性代数方程组.

步骤5：借助于数学符号计算软件Maple,求解上述过程中得到的代数方程组，可求得上述未知参数.

步骤6：将上述得到的解的情况代入到(3)和(4)中,求解出了方程(1)的孤波解.

步骤7：通过作图,分析所得解的动力学特征.

2 求解过程

现在研究(3+1)维potential YTSF方程

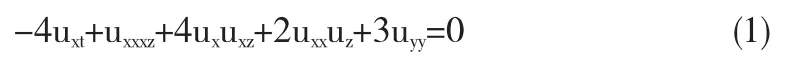
进行以下函数变换

其中f(x,y,z,t)是一个待定未知的函数.

把(2)带入方程（1）,计算化简得

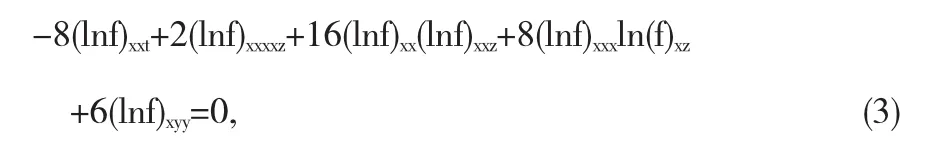
两边同时对x进行一次积分,得

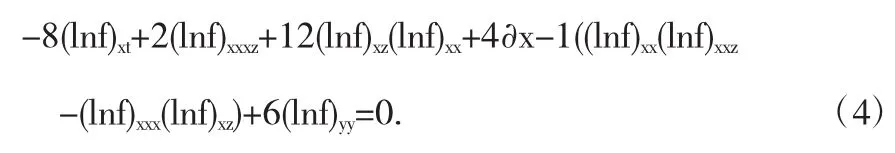
于是,方程（3.4）可以简化成

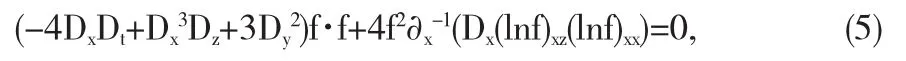
其中,运算符号D的定义为

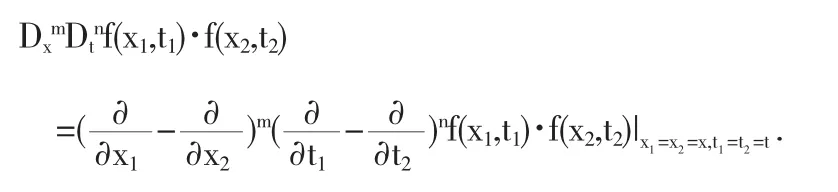
为了使方程（5）的形式更接近Hirota的双线型式[7],我们假设

为了使方程（1）存在解,我们必须将方程（6）考虑进代数系统方程组中[8],因此,方程（5）简化为如下的Hirota的双线型式

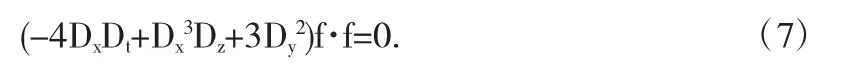
对于方程（7）运用同宿测试法寻找如下形式的解

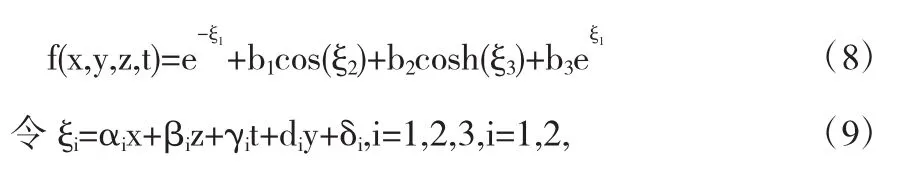
αi,βi,γi,di,bi,δi分别是待定常数.

把方程（9）和（8）替换带入方程（7）和（6）,然后计算合并同类项,令e-ξ1,eξ1,cos(ξ2),sin(ξ2)，sinh(ξ3)，cosh(ξ3)的系数为零[9],可以得到一组代数方程,关于未知数αi,βi,γi,di,bi,(i=1,2).

从方程（7）可以得到如下方程:

通过假设,从方程（6）可以得到如下方程:

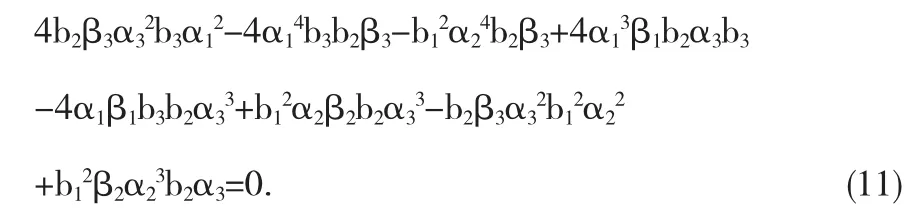
运用数学符号计算软件Maple[10],求解以上方程（10）和（11），得到如下几种解的形式：

情况1：

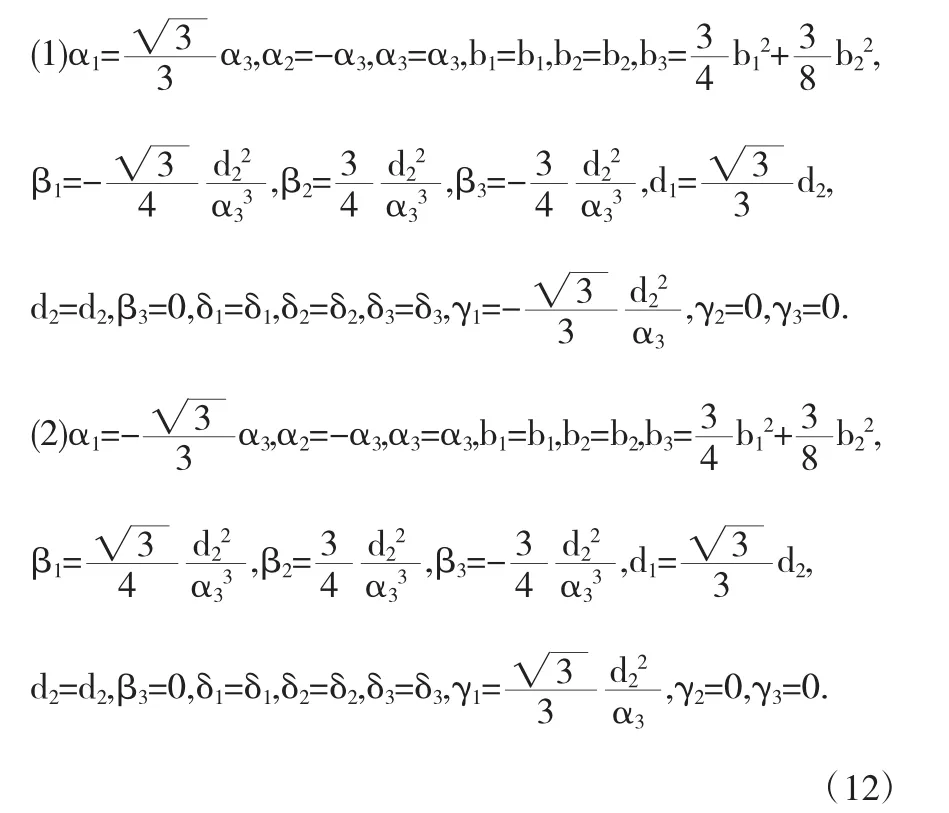
把方程（12）代入方程（2）利用方程（8）,得到的解如下所示

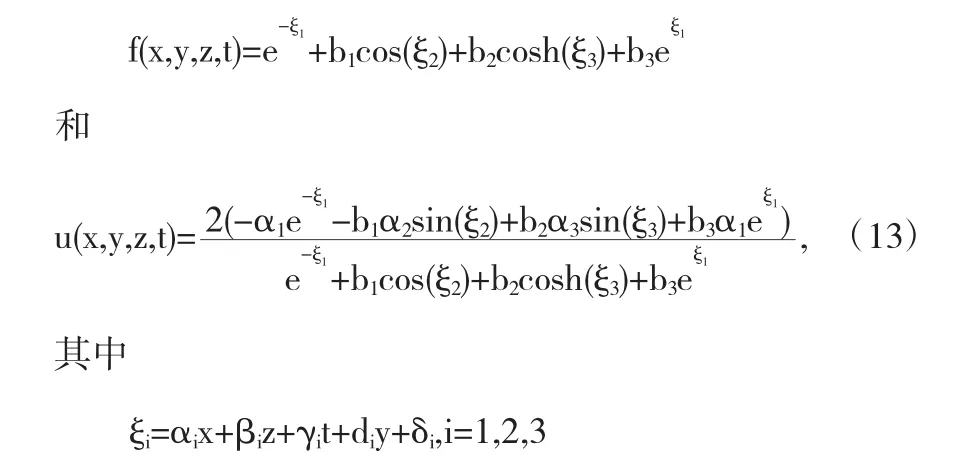
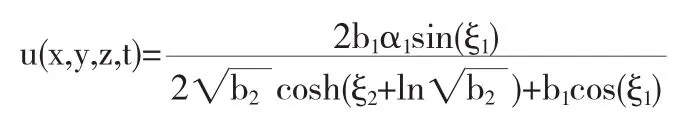
如果3d12＞4d22+4α1γ1b2,得到的扭结周期双孤子解如下所示

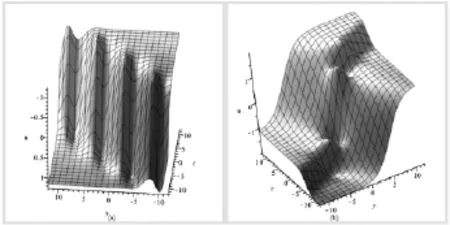
图1 解（12）当α3=b1=b2=d2=1,δ1=δ2=δ3=0.(a),x=z=0,t=x=0

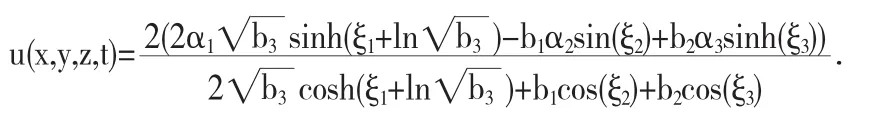
情况2:

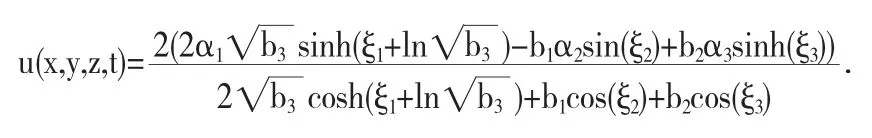
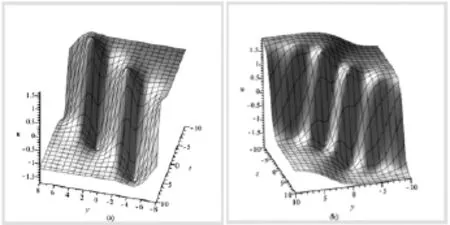
图2 解（14）当α3=b1=b2=d2=1,δ1=0,δ2=0,δ3=0.(a),x=z=0,t=x=0

3 总结

运用同宿测试法，求解出3+1维 potential Yu-Toda-Sasa-Fukuyama方程的扭结波解，可将此方法推广于一般的非线性不可积偏微分方程.

〔1〕Z.D.Dai,J.Liu,D.L.Li,Applications of HTA and EHTA to YTSF Equation,Applied Mathematics and Computation.207(2009)360-364.

〔2〕Ablowitz M J,SegUrH,Solitonsand Inverse Seattering Transform[M].PhiladelPhia,1981.

〔3〕Russell J S.Report on Waves [M].Rep.14th.Meet.Brit.Assoc.Adv.Sic.York,London:John Murray, 1844,311-390.

〔4〕傅海明,戴正德.耦合Klein-Gordon-Schrodinger方程的新精确解[J].西北师范大学学报(自然科学版),2009,45(6): 32-34,42.

〔5〕傅海明,戴正德.(2+1)维Nizhnik-Novikov-Veselov方程的新解[J].石河子大学学报(自然科学版),2009,27(3):376-378.

〔6〕Zhou Yu-bin,Wang Ming-liang,Wang Yue-ming.Periodic wave solutions to a coupled KdVequations with variable coefficients[J].Physics Letters A,2003,308:31-36.

〔7〕Wang Ming-liang,Zhou Yu-bin.The periodic wave solutions for the Klein-Cordon-Schrodingerequations[J].Physics Letters A,2003,318:84-92.

〔8〕郭玉翠.非线性偏微分方程引论[M].北京:清华大学出版社,2008.

〔9〕刘秉正,彭建华.非线性动力学[M].北京：高等教育出版社,2005.

〔10〕王红艳,李春霞,赵俊宵,虞国富.孤子理论中的直接方法[M].北京:清华大学出版社,2008.

O175.29

A

1673-260X（2016）12-0001-03

2016-09-24