压缩感知宽带接收机的电路字典基获取技术
2017-01-10王桂良陆路希
王桂良,陆路希,乐 波,郑 辉
(盲信号处理重点实验室,四川成都 610041)
压缩感知宽带接收机的电路字典基获取技术
王桂良,陆路希,乐 波,郑 辉
(盲信号处理重点实验室,四川成都 610041)
研究压缩感知用于信号采样的工程化问题,给出了MWC(Modulated Wideband Converter)结构压缩感知宽带接收机的具体设计方案,提出了字典基自环测量获取方法和字典基的时延估计补偿算法,有效解决了工程化中因观测电路存在传输时延、通带波纹等与理论观测矩阵不一致,导致压缩感知处理数字调制信号时存在重构畸变的问题.实验测量了接收机的频率覆盖范围,验证了压缩感知的有效性,并以QPSK(Quadrature Phase Shift keying)信号解调误码率为标准量化评估了压缩采样造成的信号质量损失.
压缩感知;字典基;时延差补偿;宽带接收机
1 引言
近年来,压缩感知理论[1]在特定信号的稀疏变换域和稀疏表示方法,压缩观测矩阵设计和重构算法三个方面已取得了大量理论成果,与此同时该理论的工程转化也逐渐受到越来越多的关注.
压缩感知工程化的核心问题是如何在采样前端实现观测矩阵.针对电信号压缩采样,莱斯大学Kirolos提出了一种AIC(Analogy-to-Information Converter)结构[2],以色列理工学院Mishali等人进一步将这种结构推广为多通道的形式,提出了MWC(Modulated Wideband Converter)结构,并设计了压缩采样接收机Xampling[3,4].莱斯大学Davenport等人研究高斯白噪声环境下的模拟信号采样问题,给出了压缩率每降低1/2,因带内噪声放大信号质量至少损失3dB的结论[5,6],Ray Maleh等人的研究成果进一步验证了该结论的正确性[7].
MWC类结构是观测矩阵运算的直接转化,物理意义清晰,组成简单,是目前最具可行性的观测矩阵设计结构,因此本文的接收机采用MWC结构进行设计.文献[3,4]中的MWC结构未考虑实际电路压缩字典基的获取,这样的结构在测试信号为单音或者多音等简单周期性信号时可以正常工作,但对于携带信息的数字调制信号(如MPSK、QAM等),模拟器件延时造成的字典基时延差变化、实际滤波器非理想矩形的频率响应都会带来信号重构畸变.Chen等人针对非理想矩形响应的滤波器提出一种数字滤波补偿算法[8],但该算法并没有考虑实际模拟电路延时影响.杨树树等人仿真分析了时延和非理想滤波器给信号重构带来的影响,并提出一种通道校正方法[9],然而他们的算法建立在观测矩阵为理想MWC结构观测矩阵且精确已知的条件下,这在实际系统实现中难以保证.盖建新[10]提出一种利用正弦响应获取实际电路压缩字典基的方法,该方法要求对压缩字典基的采样从正弦输入的零相位点开始,但在实际接收机中并不能完全保证某个采样时钟精确对准到达信号的零相位点,仍然存在采样时钟周期级的测量误差.此外,上述方法均只对简单单音/多音信号进行了可行性仿真,未对携带信息的数字调制信号进行性能验证.
针对上述问题,本文给出了接收机压缩字典基的获取方法,并完成以QPSK解调误码率为指标的实验验证,量化评估了压缩感知的信号质量损失.
2 系统设计
2.1 理论模型
经典的压缩过程表达式可写成:
yM×1=ΦM×NxN×1=ΦM×NΨN×NαN×1
(1)
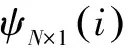
式(1)可视为一个N元一次方程组,方程个数为M,ΦM×NΨN×N和yM×1为已知参数,αN×1是需要求解的N元未知向量.当αN×1中非零元素个数小于等于M且非零元素的位置已知时,方程组超定或正定,可直接求解,否则方程组欠定,没有唯一解.压缩感知即研究αN×1中非零元素较少但位置未知条件下,方程组的求解问题.在众多求解算法中,OMP算法[11]因其较低的运算量,较高的重构精度和较好的通用性得到广泛应用.在稀疏向量位置已知的情况下,OMP算法退化为最小二乘解,是理论上的最优解,因此本文采用OMP算法求解方程重构信号.
以上经典压缩采样过程未考虑噪声影响,但噪声在实际应用中不可避免,根据引入位置噪声可分为输入噪声(信道噪声以及天线和射频端因接收机物理温度高于绝对零度而引入的噪声等)和测量噪声(压缩观测过程引入的额外噪声),输入噪声客观存在且对通信质量影响明显,在压缩感知研究中不应忽略.Davenport等人综合考虑上述噪声影响,建立新的压缩采样噪声模型
yM×1=ΦM×N(xN×1+nN×1)+eM×1
(2)
eM×1代表测量噪声,nN×1代表输入噪声,并从理论上得到了nN×1为高斯白噪声时,压缩率每降低1/2,信号质量至少损失3dB的结论[5,6].
2.2 MWC结构
将压缩感知用于信号采样时,压缩观测的矩阵运算在采样前端完成.典型的随机观测电路有AIC结构和MWC结构,其中MWC结构如图1所示.图中共有Q个采样通道,对应各有一个独立的伪随机序列pi(t),pi(t)周期等于变换域ΨN×N的基向量周期,周期内共有N个码片,码片速率等于Nyquist采样率,每个通道在一个伪随机周期内采样K个样点,共同构成M=QK个压缩采样点.第i个通道采样可表示为:
(3)
离散近似形式为:
(4)
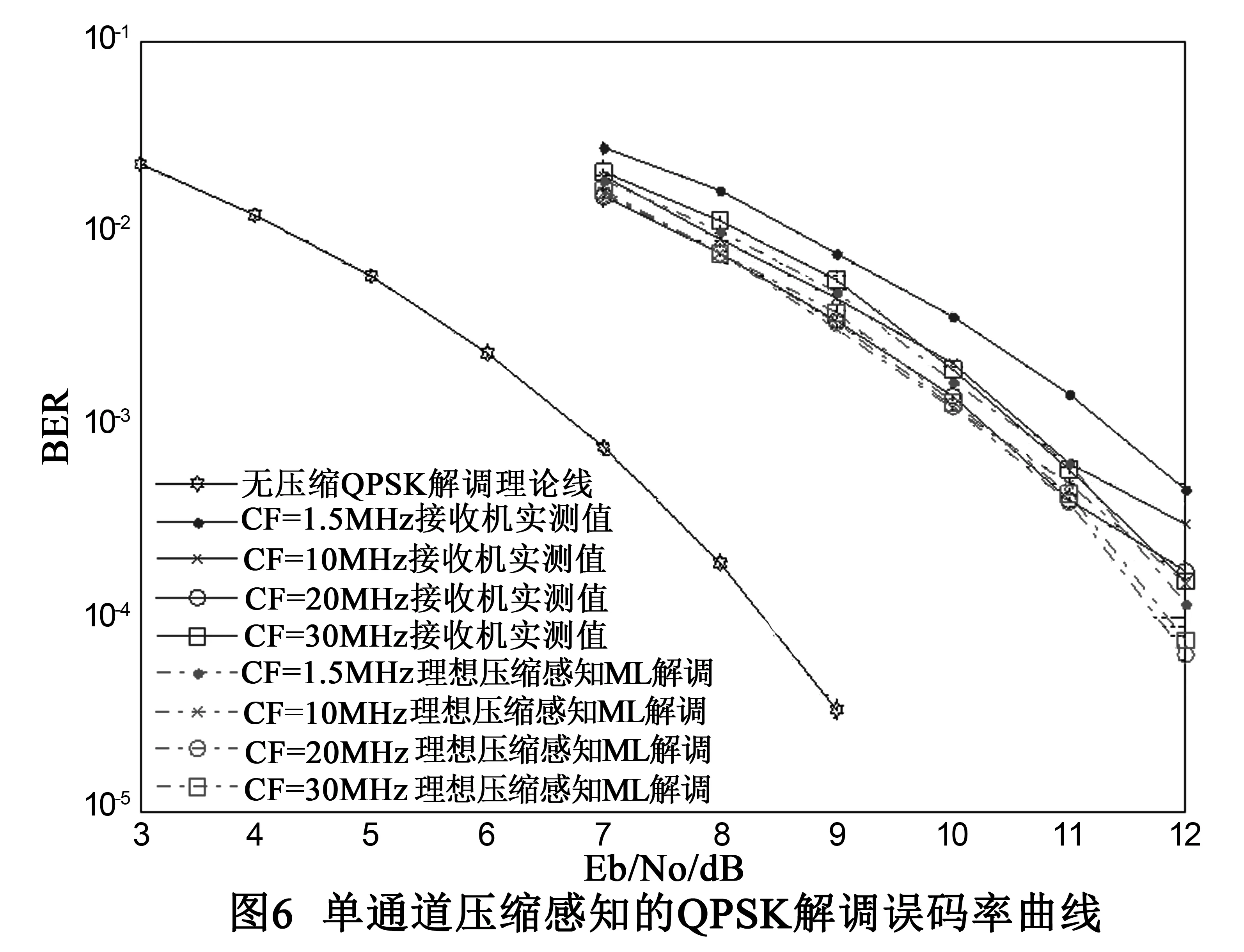
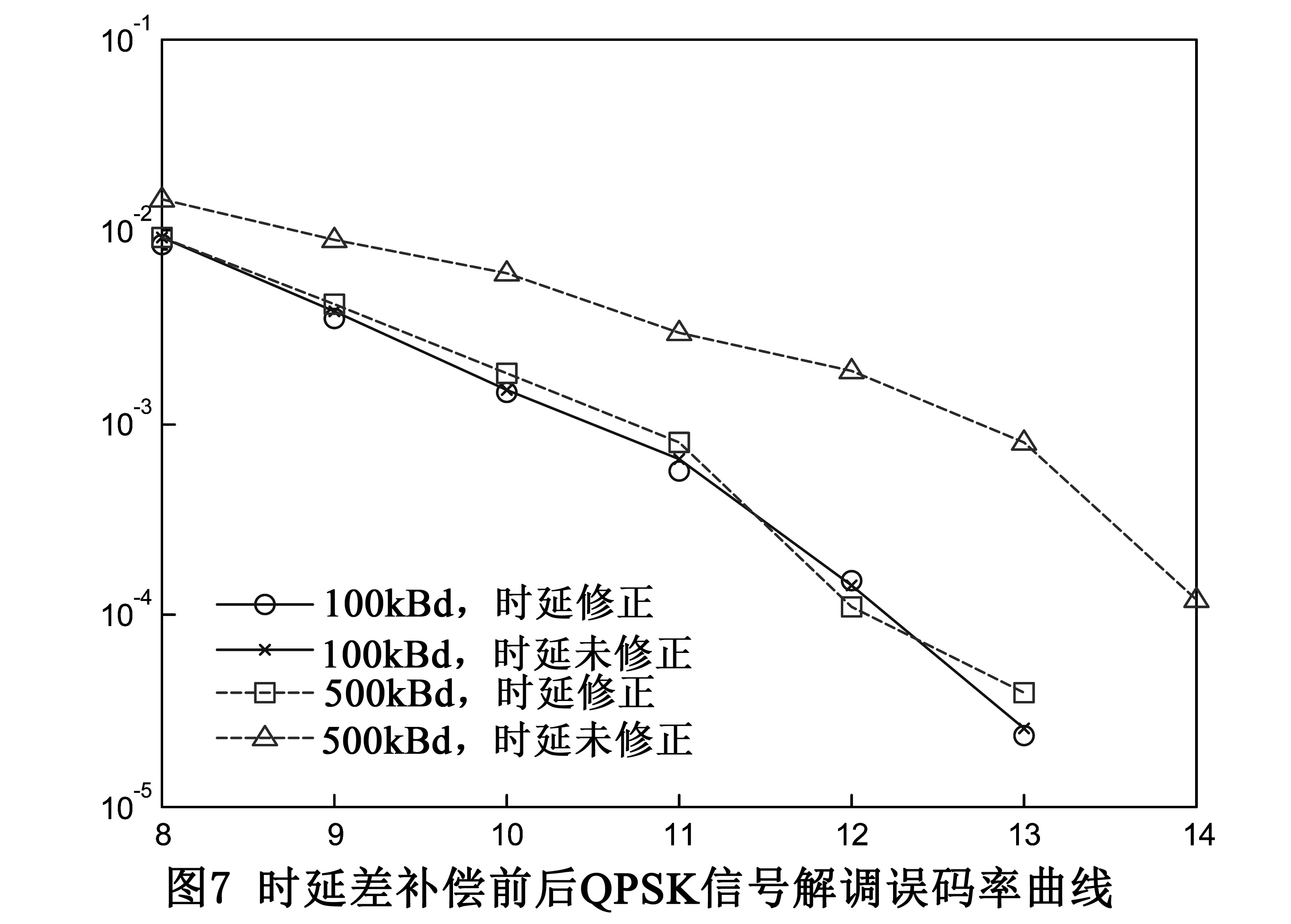
其中等效L+1阶FIR滤波器系数为{hi(0),hi(1),...,hi(L)},由于滤波器的效应,当前采样值与先前L时间内的输入均有关.假设L (5) 其中Φi,K×N为通道i的观测矩阵,其元素值为: k∈{1,2,…,K},τ∈{1,2,…,N} (6) 由于pi(τ)是伪随机的,该观测矩阵具有伪随机性,只是存在部分零项. 伪随机周期序列在频域上表现为梳状谱,谱线频率间隔等于周期的倒数,它与输入模拟信号时域相乘即两者的频域卷积,等效于整个频段乘以不同的系数再经过不同频移叠加在一起,在滤波器通带范围内形成若干个窄带线性叠加副本,采样后不同频段上的信号成分并不丢失,只是被混叠在了一起,具备重新分离重构的可能[6]. 2.3 压缩感知接收机设计 根据MWC结构,我们设计了一套压缩感知接收机,该接收机支持单通道压缩采样和双通道压缩采样,整体采样率固定为40MSps,单通道工作时AD采样速率为40MSps,双通道工作时2个AD的采样速率各为20MSps,对应原始Nyquist速率80MSps,压缩率1/2,目标覆盖频率范围1.5MHz-30MHz,其组成如图2所示. 除了两路AD通道外,该接收机还具有2路伪随机周期序列输出和1路字典基自测信号DA输出.伪随机周期序列采用TTL双电平表示01序列,每个周期6.4μs,含512个符号,符号速率等于目标Nyquist采样率80MSps.字典基自测信号的周期同为6.4μs,具体形式为512组不同频率和初始相位的单音信号,为了保证自测信号具有较好的模拟输出波形(特别是对高频单音信号),DA回放速率为240MSps. 压缩观测电路即观测矩阵的电路实现,包括电平转换器、乘法器和低通滤波器三部分.电平转换器采用TI公司的LVDS驱动芯片SN65LVDS047,用于将单极性(0V、2.5V)TTL伪随机序列电平转换为双极性(-1V、1V)电平.由于伪随机观测序列是80MSps双极性方波,频谱较宽,所以选用ADI公司的四象限宽带乘法器AD835,支持3dB频率范围DC-250MHz的两个信号的相乘运算.低通滤波器采用腔体滤波器,3dB通带范围DC-18MHz. 接收机工作流程如图3所示.上电后首先将DA输出端与信号输入端连接,进行字典基自测.测量完毕后,再将外部输入信号与输入端连接,进行正常的压缩采样.压缩采样的数据先存盘,事后通过软件完成离线波形重构,恢复成等效Nyquist速率(80MSps)的采样数据并再次存盘.二次存盘后的数据即可进行常规信号检测、解调等处理.此外,接收机还支持已知载频和调制速率,且调制速率不超过150kBd的QPSK信号实时解调. 3.1 字典基自测方法 实际电路由于输入信号、伪随机序列的传输时延、滤波器幅频、相频响应、通带波纹、器件驱动时钟时差等因素,无法精确计算压缩观测电路的字典基,为此我们设计了字典基自测功能,通过工控机自环发射测量信号,将其经过压缩观测电路后的采样波形作为当前电路的字典基. 本接收机的稀疏表示变换域选用实数形式的傅里叶变换域,目标Nyquist采样率为80MSps,伪随机周期序列符号数为512,因此字典基自测信号为512组不同频率的正弦(初相为-90°)和余弦(初相为0)信号,频率为80f/512MHz,f=0,1,2,…,255,共同组成一个完备的傅里叶基集合.DA回放速率设为240MSps,一个6.4μs周期共1536个符号,具体形式为 (7) 其中k表示余弦和正弦的切换,取值为0或1.自测时,每个自测信号连续发送若干个周期,将收到的若干个周期的采样序列按位平均得到最终的测量结果.同一频率的正弦和余弦信号组成1个复数形式傅里叶基向量用于稀疏表示和重构波形. 为保证不同时钟速率的DA自测波形和AD测量结果的稳定,采用同源钟(但时钟速率不同)驱动DA和AD,同时每个DA输出周期起始标记1个时标信号,内部传输给AD用于标记AD采样波形的周期起始位置,即每个周期完成一次时间校准,确保自测过程不存在较大的时钟漂移,测量结果稳定没有滑码,如图4所示.实测发现该时延差每次上电并不相等,但上电后保持恒定,因此接收机每次上电均需进行字典基测量. 3.2 字典基时延差重构失真 自测信号和时标的传输路径不同,存在时延差,导致字典基的初相与自测用稀疏表示基向量初相不一致,若仍以0初相为起始的稀疏表示基向量重构波形,会产生重构失真,本节对此进行分析.为便于描述,我们从式(1)出发,自测信号、字典基和稀疏表示基直接采用复数形式. (8) 其中N=1536,f=0,1,2,…,255.该向量周期不间断发送,经过时延τ后,在时标信号驱动下采样得到周期字典基向量为 (9)其中e-j2πfτ/N表示自测信号因时延差产生的相位变化.自测信号功率较大,可忽略噪声影响,但由于伪随机观测的原因,θM×1(f)近似于噪声,无法直接提取时延信息.这里不考虑观测矩阵传输时延的影响,因为观测矩阵时延后,仍然是伪随机观测矩阵,性质没有发生变化.重构用的稀疏表示基向量与发射自测向量相同为ψN×1(f). 假设目标信号到达观测矩阵时的输入为: xN×1=a1ψN×1(f1)+a2ψN×1(f2) (10) 其中a1和a2为该信号在频率f1和f2的复数响应.观测结果为: yM×1=ΦM×N(a1ψN×1(f1)+a2ψN×1(f2)) (11) 则f1的字典基响应为: R(f1) (12) R(f2)≈a2Nej2πf2τ/N/Q (13) (14) 与式(10)原始波形相比,频率f1和f2的响应产生了类似群时延的相位变化,造成重构失真,若调制信号的带宽较宽,需多个基响应表示,则这种失真会造成该信号重构质量损失. 3.3 自测字典基时延差估计和补偿 为避免字典基时延差τ造成的信号重构失真,需要对其进行估计补偿.考虑实际电路实现,我们从式(4)出发,对于通道i,频率f的自测字典基第k个采样值表示为: (15) A(f)e-j2πfη/N表示以下序列在频率f的响应 (16) 其中A(f)和-2πfη/N分别表示其幅度和相位响应,式(15)没有将伪随机周期序列pi(n)的时延列入计算,因为该序列时延后等效于一条没有时延的新的伪随机周期序列,性质没有发生变化.除了传输时延τ外,观测电路也会带来群时延,记为η,根据实测结果,该值在关心的频率范围内基本恒定.对θi(k,f)序列进行本地下变频,并与相邻频率的变频后结果进行对应位置差分即可得到当前时延的估计值: =τ+η (17) (18) (19) 接收机在实验室环境进行测试,在数字域直接产生含噪调制信号用任意波形发生器E4438C转化为模拟信号做信号源.压缩采样后,通过软件离线重构成等效于80M采样率的采样文件,再用后端处理软件进行分析. 首先利用跳频信号验证接收机的频率覆盖范围.为了便于观察,用E4438C产生一个顺序跳频信号,共12个频点,覆盖1MHz~30MHz频率范围,跳速1000跳/秒,QPSK调制,调制速率100kBd,每跳198个比特,两跳间存在0.01ms保护间隔,无噪声.图5给出了该信号的压缩采样文件和重构后的波形文件时频图,受压缩观测的影响,压缩采样波形近似于全带噪声.采用OMP算法重构后生成等效于80MSps Nyquist采样的波形文件,该文件的时频图上清晰可见目标跳频信号,验证了压缩感知接收机可覆盖超过1/2采样率的频率范围的能力.由于跳频信号频率切换可能发生在某些重构周期中间,即该周期包含了前后跳的各一部分,非稀疏响应个数增加而值变小,造成重构出错,导致时频图上出现杂散点. 接下来通过解调误码率测试接收机性能.测试信号为定频QPSK信号,调制速率100kBd,在1.5MHz-30MHz内选取了4个典型载频进行单通道40MSps压缩采样.为了公平评价压缩感知性能,测试中采用频带范围为0.5MHz~31MHz的宽带噪声,略宽于目标覆盖带宽1.5MHz~30MHz.该实验需做3点说明:(1)虽然测试信号是定频信号,但压缩感知理论的前提是稀疏响应位置未知,因此这里采用宽带噪声进行测试,若前端可利用先验载频位置做窄带滤波,则可采用传统的变频和带通采样完成信号无损低速采样,无需压缩感知技术;(2)为避免重构算法不佳带来的额外损失,我们直接设定非零稀疏响应位置并用最小二乘法重构信号,由于宽带噪声的存在,此时最小二乘解是最小均方误差解,是重构可达到的最优解;(3)为避免解调算法不佳带来的额外损失,我们利用测试信号先验信息进行ML(最大似然)解调,经验证该解调方法在普通采样时可达到QPSK的理论性能.因此,实验中的损失可认为主要是压缩感知本身造成的信号质量恶化和硬件实现的损失. 压缩感知宽带接收机解调误码率实测值、理想压缩感知ML解调和无压缩QPSK解调理论线的比较如图6所示.其中仿真得到的理想压缩感知ML解调误码率与接收机实测值的区别在于理想压缩感知接收机无延时和通带波纹,它的压缩字典基和信号传输根据式(1)直接计算得到.在稀疏响应位置已知,解调采用ML解调的情况下,理想压缩感知ML解调即为MWC结构压缩感知所能达到的理论极限性能.图10中接收机实测结果仅比理想压缩感知ML解调差1dB,表明本接收机经过字典基校准后性能接近理想情况,考虑到仿真中的噪声是数字全带AWGN噪声,比实验时的噪声略宽,实际接收机的实现损失略大于1dB.对比无压缩QPSK解调理论线,理想压缩感知ML解调信号质量损失达3.5dB,文献[8,9]指出理论上AWGN噪声下每压缩1/2采样率信号带内噪声放大3dB,多个非零稀疏响应的字典基向量自身非正交还会产生额外的混叠损失,本实验结果与该理论结论相符.进一步的实验和仿真显示,双通道的性能比单通道差约1dB,此外随着信号调制速率的提升,非零稀疏响应的个数增加,也会造成信号自身混叠进一步恶化. 最后验证字典基获取和补偿方法的效果.图7给出了时延差补偿前后,载频15MHz、符号速率分别为100kBd和500kBd的QPSK信号解调误码率实测曲线.图中100kBd信号时延补偿和未补偿的曲线基本重合,时延差补偿对100kBd信号解调影响不大,这是因为系统中一个字典基的频率分辨率为156kHz,与100kBd的QPSK信号带宽接近,因此在一个压缩周期内,100kBd信号仅在1~2个相邻字典基上有较大响应,时延差引起的重构畸变程度较轻.而500kBd信号带宽覆盖5~6个字典基,时延造成的解调性能损失可达2dB,采用本文的时延补偿方法后,500kBd信号的解调性能提升至与100kBd信号基本一致的水平,证实了本文字典基获取和补偿方法对实际观测电路的有效性. 本文根据压缩感知原理研制实现了一套MWC结构的接收机,给出了具体设计方案,针对采样前端观测电路存在传输时延、通带波纹等因素造成实际电路字典基与理论观测矩阵不一致的问题,设计了自环测量的压缩字典基获取方法,理论分析了电路传输时延导致的重构失真,并给出了该时延差的估计和补偿算法.实验验证了接收机以40MSps采样率无混叠覆盖1.5MHz~30MHz频率范围的能力,并以QPSK解调误码率为标准量化评估了压缩采样造成的信噪比损失,验证了压缩感知理论中在AWGN噪声下,压缩率降低1/2,因带内噪声放大信号质量至少损失3dB的结论.本文接收机实验进一步论证了压缩感知应用于信号采样的可行性和代价,对今后此类系统实用具有重要参考价值. [1]E Candès,J Romberg,T Tao. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Trans Inf Theory,2006,52(2):489-509. [2]J Laska,S Kirolos,M Duarte,et al. Theory and implementation of an analog-to-information converter using random demodulation[A]. IEEE Int Symp on Circuits Syst (ISCAS)[C]. New Orleans,Louisiana:IEEE,2007. 1959-1962. [3]M Mishali,Y C Eldar,A J Elron. Xampling:Signal acquisition and processing in union of subspaces[J]. IEEE Trans Signal Process,2011,50(10):4719-4734. [4]T Michaeli,Y C Eldar. Xampling at the rate of innovation[J]. IEEE Trans Signal Process,2012,60(3):1121-1133. [5]J Treichler,M Davenport,R Baraniuk. Application of compressive sensing to the design of wideband signal acquisition receivers[A]. 6th US/Australia Joint Workshop on Defense Appl Signal Process (DASP)[C]. Lihue,Hawaii:DASP,2009. 1-7. [6]M Davenport,J Laska,J Treichler,R Baraniuk. The pros and cons of compressive sensing for wideband signal acquisition:noise folding versus dynamic range[J]. IEEE Trans Signal Process,2012,60(9):4628-4642. [7]R Maleh,G L Fudge,F A Boyle,P E Pace. Analog-to-information and the Nyquist folding receiver[J]. IEEE J Emerging and Sel Topics Circuits Syst,2012,2(3):564-578. [8]Y Chen,M Mishali,Y C Eldar,A O Hero. Modulated wideband converter with non-ideal lowpass filters[A]. IEEE Int Conf on Acoustics Speech and Signal Processing (ICASSP)[C]. IEEE,2010. 3630-3633. [9]杨树树,宁勇. 基于MWC压缩采样系统的通道失配校正研究[J]. 航天电子对抗,2015,31(3):37-39,48. S Yang,Y Ning. Study on channel mismatch correction based on MWC compressive sampling system[J]. Aerospace Electronic Warfare,2015,31(3):37-39,48.( in Chinese) [10]盖建新. 基于MWC的稀疏宽带信号亚奈奎斯特采样技术研究[D]. 黑龙江哈尔滨:哈尔滨工业大学,2013. J Gai. Research on MWC-based Sub-Nyquist Sampling Technology of Sparse Wideband Signals[D]. Harbin,Heilongjiang:Harbin Institute of Technology,2013.(in Chinese) [11]J A Tropp,A C Gilbert. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Trans Inf Theory,2007,53(12):4655-4666. 王桂良 男,1987年9月出生,山东潍坊人. 2009年6月获清华大学工学学士学位,现盲信号处理重点实验室博士研究生,研究方向:稀疏信号处理、辐射源指纹识别. E-mail:wangguiliang05@gmail.com 陆路希(通信作者) 男,1982年9月生于上海.2011年6月获北京大学工学博士学位,现盲信号处理重点实验室工程师,研究方向:跳扩频信号处理、稀疏信号处理. E-mail:luluxi@pku.edu.cn 乐 波 女,1970年9月生于四川绵阳.2009年6月获电子科技大学工学博士学位.现盲信号处理重点实验室高级工程师,研究方向:电磁频谱监测. 郑 辉 男,1957年3月生于重庆.盲信号处理重点实验室高级工程师、博士生导师,研究方向:盲信号处理、信息与通信网络. The Circuit Dictionary Basis Acquisition for the Compressive Sensing Wideband Receiver WANG Gui-liang,LU Lu-xi,YUE Bo,ZHENG Hui (NationalKeyLaboratoryofBlindSignalsProcessing,Chengdu,Sichuan610041,China) The implementation of the compressive sensing was studied in this paper.Because of the transmission delay and the pass band ripple,the measurement matrix in a real compressive sensing receiver was different from that in theory.These differences caused the reconstruction error when digital modulated signals were compressively sensed.A self-loop measuring method of the circuit dictionary basis and an algorithm of time-delay compensation were proposed to solve this problem.The frequency range and the effectiveness of our compressive sensing receiver were verified through experiments.The SNR(Signal Noise Ratio) loss of the compressive sensing was also evaluated through the QPSK(Quadrature Phase Shift keying) demodulation test. compressive sensing; dictionary basis; time-delay compensation; wideband receiver 2015-02-27; 2015-12-25;责任编辑:李勇锋 中国博士后科学基金(No.2013M532238) TN95 A 0372-2112 (2016)12-2939-07 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.12.018
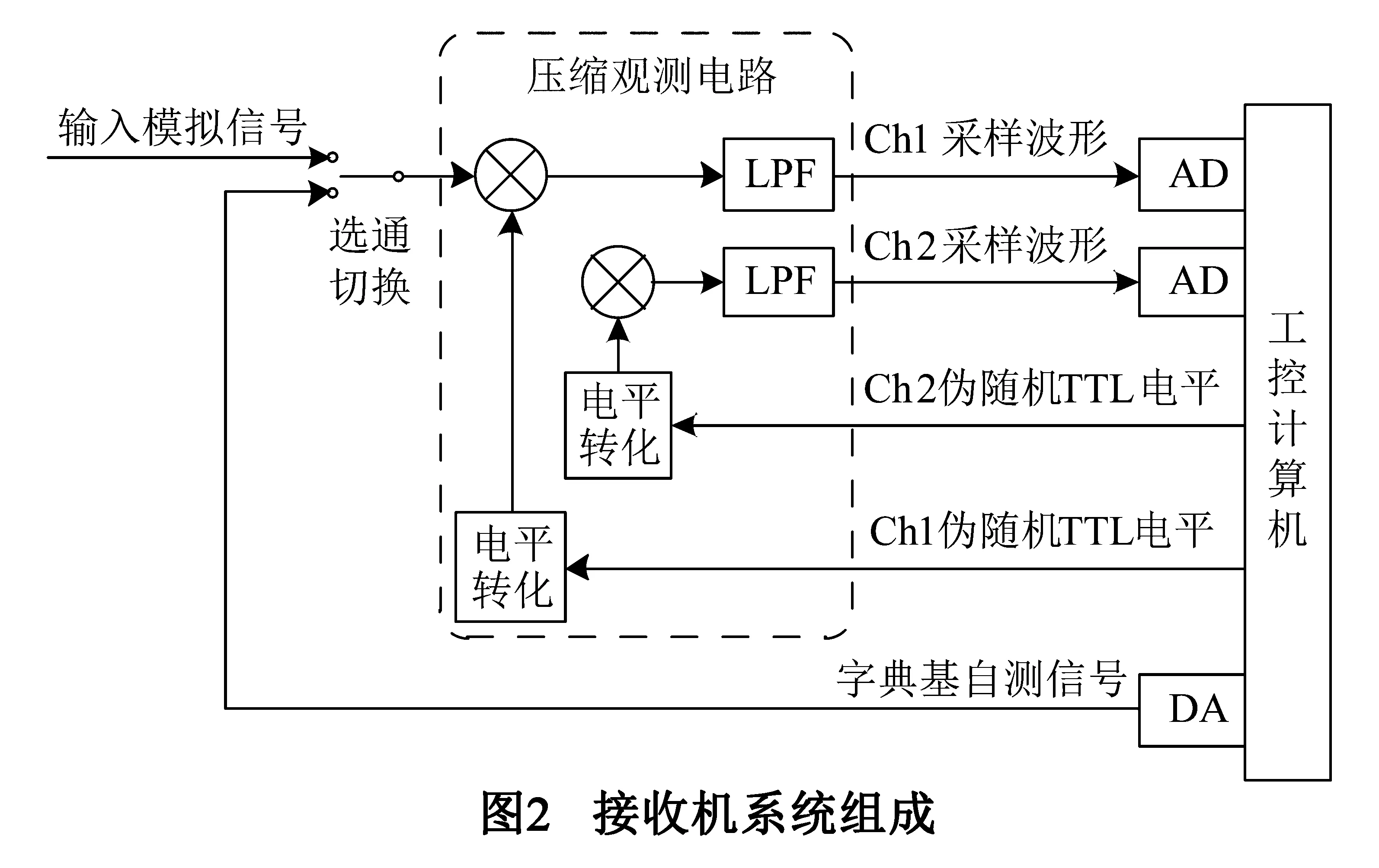

3 实际电路字典基的获取
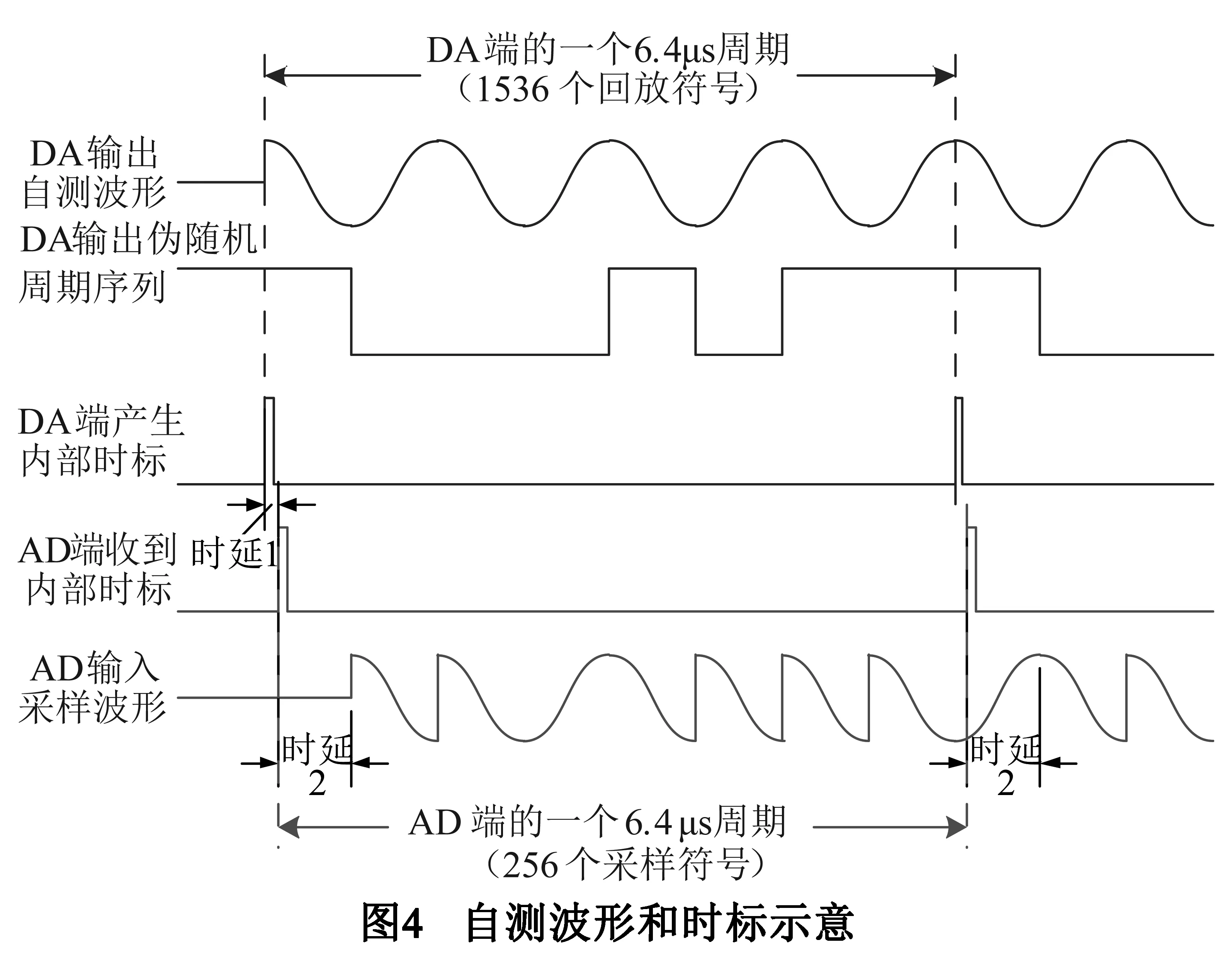
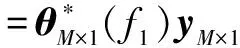
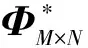
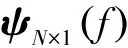
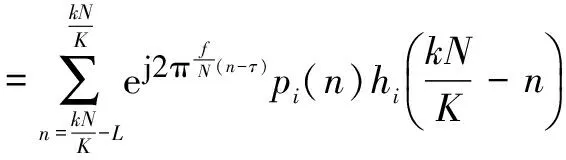
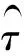
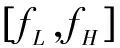
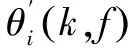
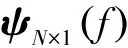
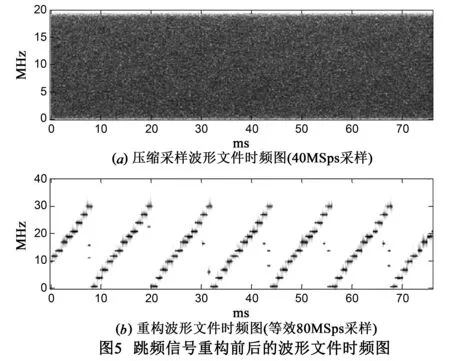
4 实验验证
5 结束语


