基于演化历史信息的自变异协同量子行为粒子群优化算法
2017-01-10赵吉,傅毅,梅娟
赵 吉,傅 毅,梅 娟
(1.无锡环境科学与工程研究中心,江苏无锡 214063; 2.江南大学物联网工程学院,江苏无锡 214122)
基于演化历史信息的自变异协同量子行为粒子群优化算法
赵 吉1,2,傅 毅1,梅 娟1
(1.无锡环境科学与工程研究中心,江苏无锡 214063; 2.江南大学物联网工程学院,江苏无锡 214122)
提出一种基于演化历史信息的自变异协同量子行为粒子群优化算法(ESH-CQPSO ).该算法采用二维空间分割树结构记录群体演化过程中的位置和适应值,借助群体之间的协同机制确保增强搜索能力,提高优化性能,防止过早收敛.通过空间分割机制可以获得一个快速的近似适应度函数.这个近似值可以提高ESH-CQPSO中的变异策略,使得相应的变异操作是一种无参数、多样性的自适应变异.对比其他传统算法,通过对标准测试函数的实验结果表明,ESH-CQPSO算法在处理多峰和单峰测试函数时具有更好的优化性能,收敛精度和收敛速度都得到了提高,证明该算法的有效性.
量子行为粒子群优化;演化历史信息;自适应变异;二维空间分割;协同方式
1 引言
近年来,量子行为粒子群优化算法(Quantum-behaved Particle Swarm Optimization,QPSO)[1]因为其算法简单,优化性能强而受到越来越多关注.类似于其他全局优化算法[2],QPSO也会受制于过早收敛至局部最优的趋势,这也是群体智能优化算法的研究热点,很多文献都是围绕这个问题展开的[3~6].深入研究发现,QPSO找到全局最优解的能力主要取决于两个方面:(1)跳出局部最优点的能力;(2)探索搜索空间的能力.为此本文提出基于演化历史信息的自变异协同量子行为粒子群优化算法(Cooperative QPSO with adaptive mutation based on Entire Search History,ESH-CQPSO )以提高QPSO算法的优化性能.
此前也有相关文献提出了利用记忆的形式使用搜索历史信息自适应地引导搜索目标[7~9],但这些研究仅仅使用了部分搜索历史信息,而未使用的信息则被丢弃了.演化搜索历史信息,包括估计解的位置和解的适应值对于提高群体智能算法的性能都是有价值的信息.从直观上看,它可以用来保持多样性,引导搜索方向或指示有希望的搜索区域.此外,当演化历史信息中出现相同的最优解时,它可以警告该搜索可能陷入局部最优.Yuen和Chow提出的非重复访问机制[10]被应用于遗传算法(Genetic algorithm,GA),从而保证非重复访问遗传算法(Continuous Non-revisiting Genetic Algorithm,cNrGA)中的解不会被重复访问.实验证明cNrGA比大多数GA算法更加优异.但该算法中的非重复访问变异操作由于子空间限制而无法充分进行搜索,为此引入协同进化方法,利用二维空间分割机制,提出基于整个搜索空间带有重叠子区域的自变异协同量子行为粒子群优化算法,进而促进粒子的充分搜索能力以提高算法性能.
2 基于演化历史信息的协同量子行为粒子群优化算法
2.1 演化历史信息方案
定义1 解x的子区域
假设x是搜索空间S中一个解,即x∈S,S被二维空间分割树(Binary Space Portioning,BSP)T划分为一组子区域H=∪ihi.如果x∈h并且h为T的一个叶节点,定义子区域h∈H为x的子区域.
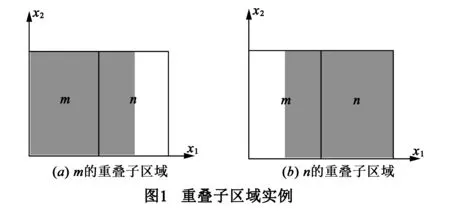
在演化历史信息方案中,所有访问过的解的位置和适应值[xi,f(xi)]都由BSP树来保存.算法迭代过程中,整个搜索空间会被划分为一组区域H.树结构中的每个节点代表了搜索空间的子区域.假设BSP树中一个父节点P有两个子节点m和n.子节点沿着第k维将P的子区域线性分割为两个叠加的子区域,k的选取满足m和n在k维上的距离最大,即k=argmax|m(k)-n(k)|.以这种方式,将QPSO算法之前产生的每个估计解记录在树的节点中.BSP树在整个解过程中就记录了搜索空间中的所有解,利用之前解的演化历史信息对当前解进行分析.随着迭代进行,BSP树会随之增长.因为树结构是依赖于每次迭代的解序列,所以BSP树是一个随机树,每次迭代的拓扑结构都不同.
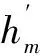
算法1 解x重叠子区域的伪代码
输入:(1)BSP树T,(2)估计解x∈RD(D为维数),(3)搜索空间S
1.h=Πj[lj,uj]:=S
2. Curr-node:=root node ofT
3. While (Curr-node有左右两个子节点m和n)
4. 根据i=argmax|m(i)-n(i)|获得分割维度i,其中i=1,…,D
5. If (|m(i)-x(i)|≤|n(i)-x(i)|)
6. Curr-node:=child nodem
7.ui:=n(i)
8. Else
9. Curr-node:=child noden
10.lj:=m(j)
11.End
12.Loop
输出:解x的重叠子区域h
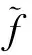
2.2 基于演化历史信息的自适应变异机制
定义2 子区域邻居
如果X⊆Y,节点y的子区域Y是叶子节点x的子区域X邻居.
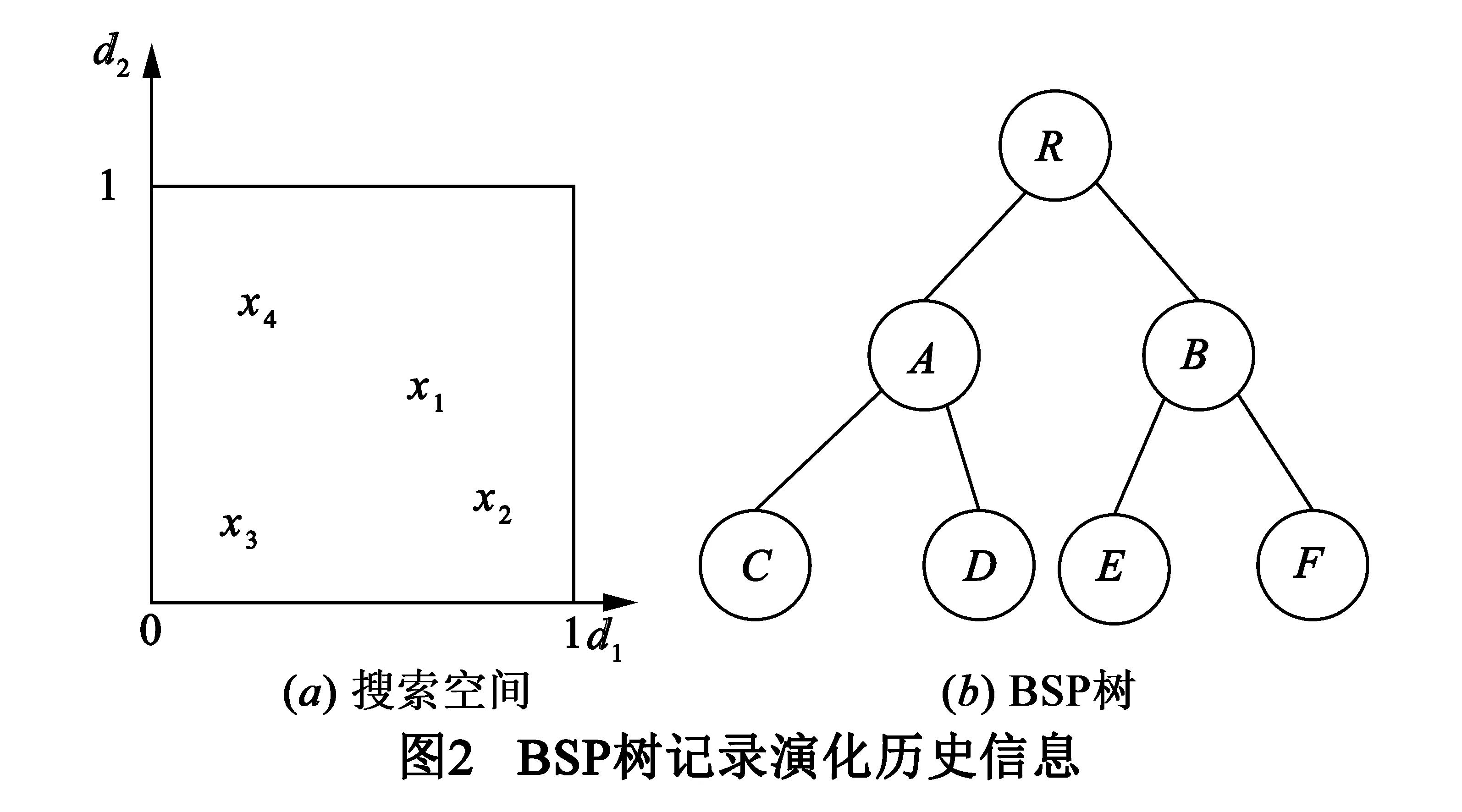
如果节点x的适应值在其子区域X的邻居中值是最小的,那么子区域X是最佳的.每一个子区域可以看作是一定邻居数量的最优值.当找到最优子区域的近似适应度值后,子区域X的变异方向被定义为指向其最近的最优子区域方向.
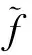
算法2 ESH-CQPSO中的变异算法
输入:(1)需要变异的粒子x,(2)BSP树T
1. {xi}:=在BSP树T中记录的粒子
2.H=∪ihi:=被分割的子区域组,其中hi是xi的子区域 /*搜索x的最近最优子区域y*/
3. 搜索x的子区域h⊆H
4. 找到h的最近最优子区域
5.y:=子区域h中的粒子 /*结束搜索x的最近最优子区域y*/
6.α:=Random(0,1)
7.x′:=αx+(1-α)y
输出:变异后的粒子x′
2.3 协同机制
搜索算法,包括随机性算法(如量子行为粒子群算法和遗传算法等)在解决规模问题的高维数据时都会遭遇“维数灾难”现象.粒子的每一个维度都会影响整体适应值.因此,即使一些粒子某些维度上的值已经非常接近全局最优解的相应维度值,但这些粒子仍然获得较低的适应值.协同运作的重要性就在于,在粒子群中“好”的维度信息得以保存,并且可以防止可能有用的信息被不必要地丢弃;其操作简单易实现,在高维问题中可以有效改善算法性能[5,6].引入动态协同机制[6],可以分别对每一维进行计算,并保存最有用的信息,以加速收敛.动态协同进化算法的程序步骤如算法3所示.
算法3 ESH-CQPSO中的协同进化算法
输入:粒子群P={p1,p2,…,pn}
1. for 粒子群中每个粒子
2. 根据QPSO算法产生5个粒子
3.pi:=pi-b选择5个中最好的粒子
4.pc=plj
5. for 每个粒子pk,k=1,…,5
6.f=f(pk)
7. for 每一维j
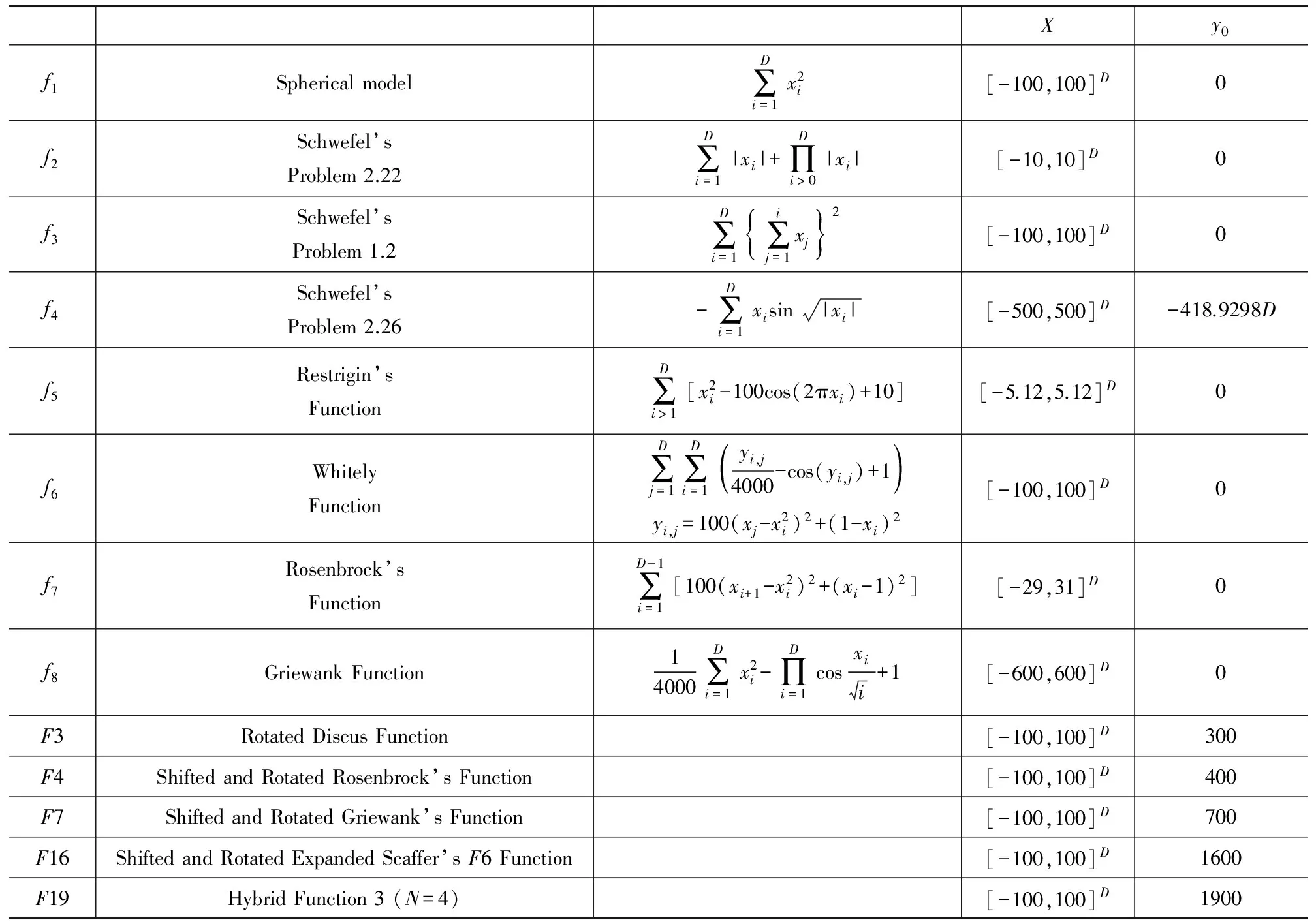
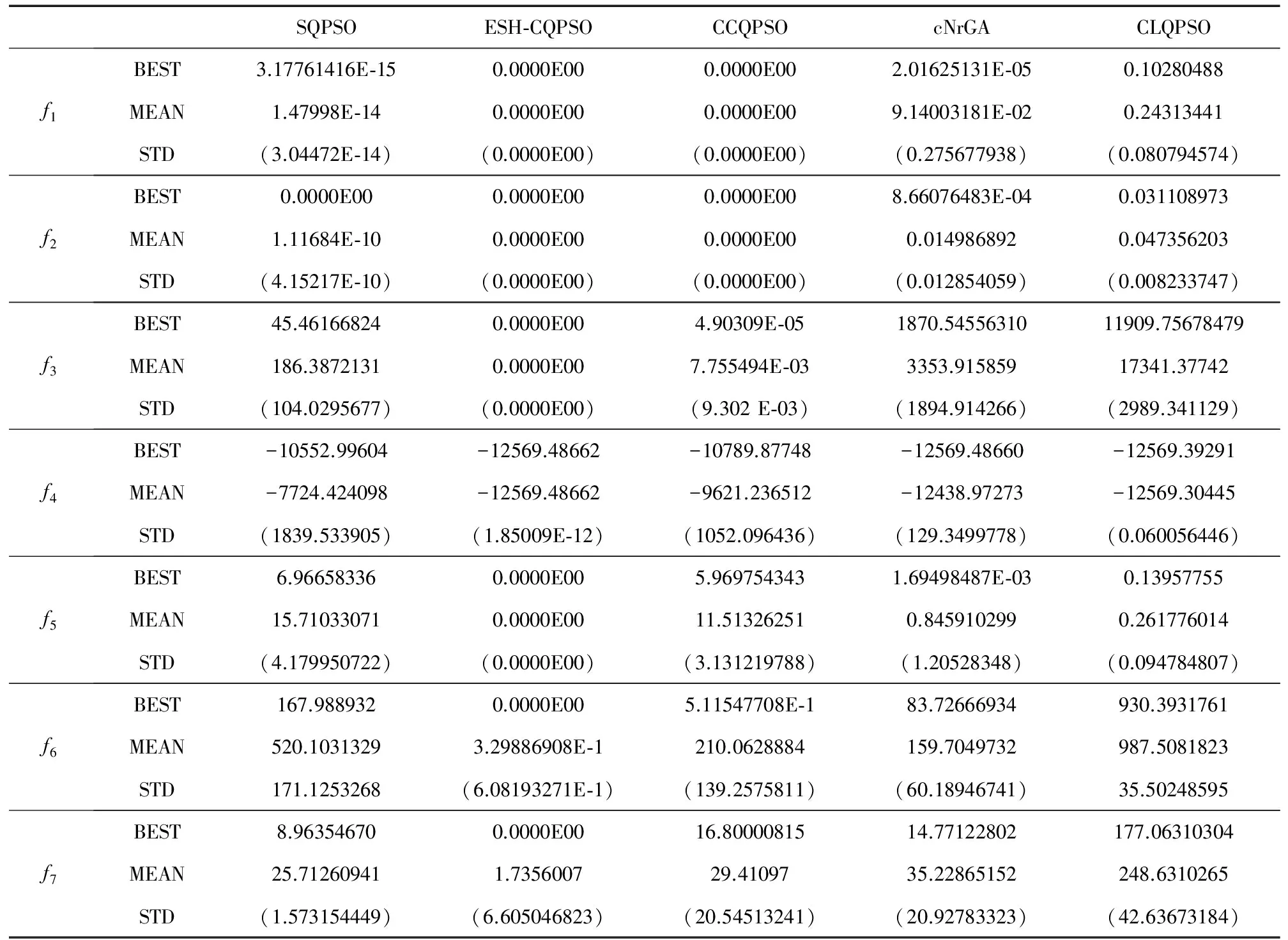
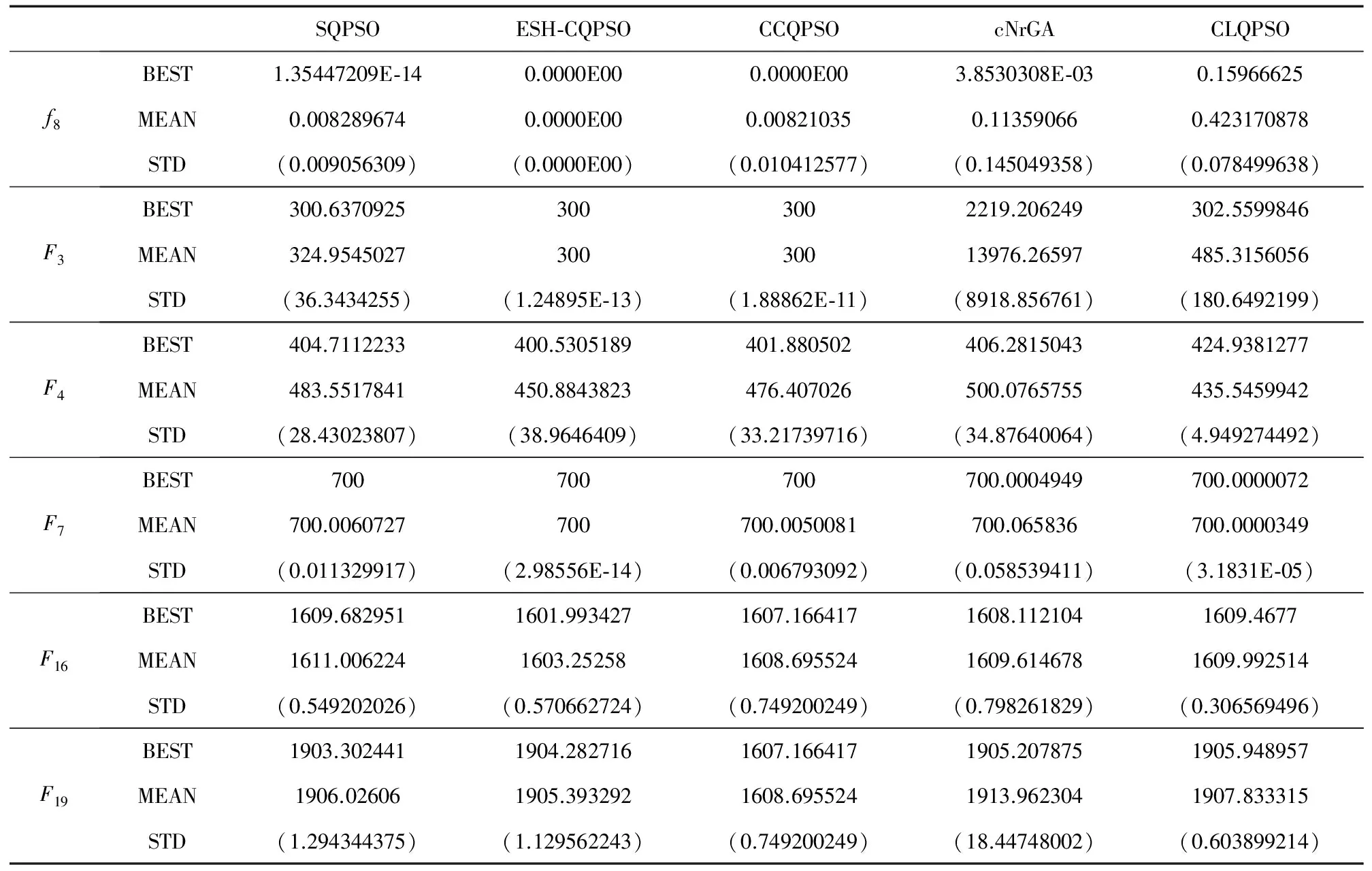
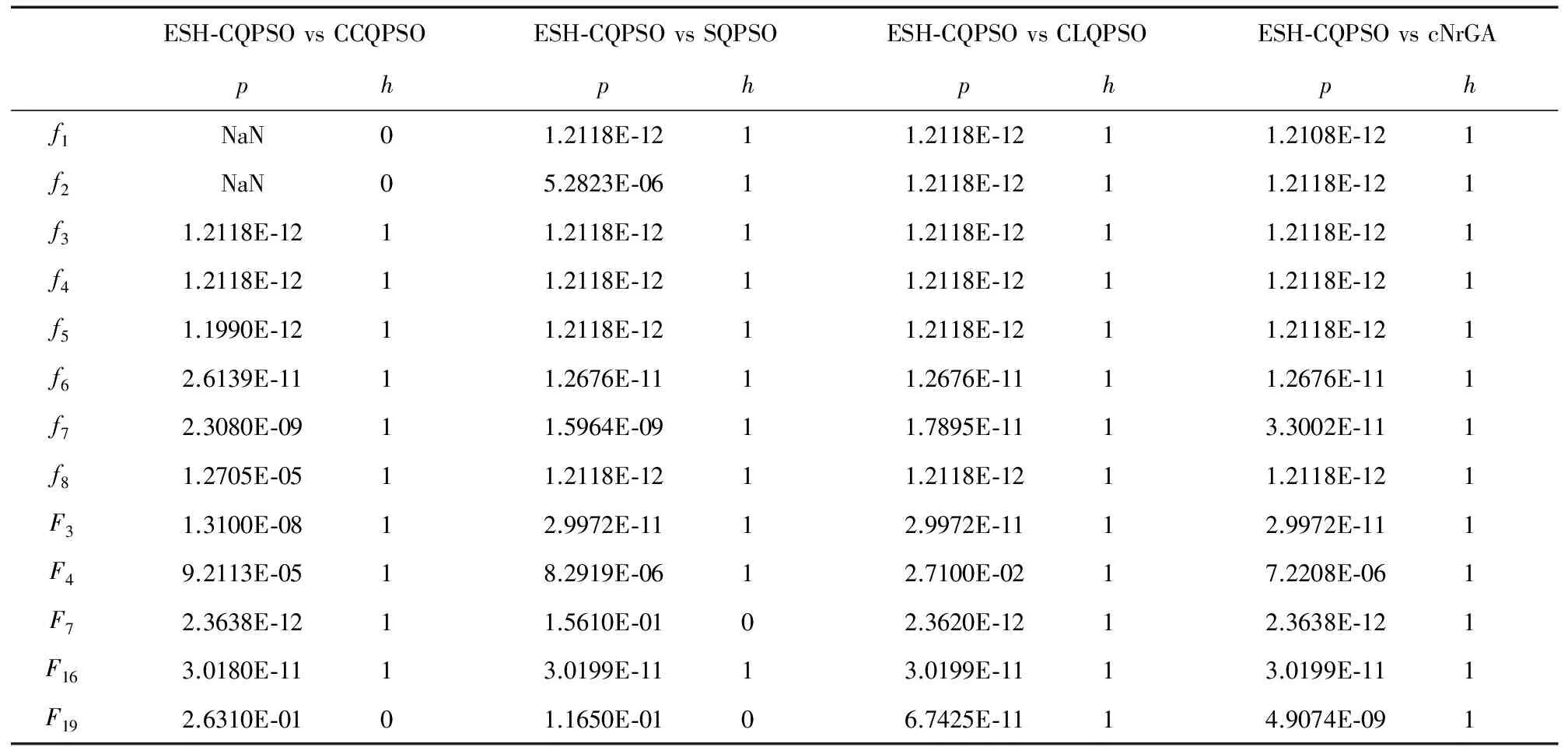
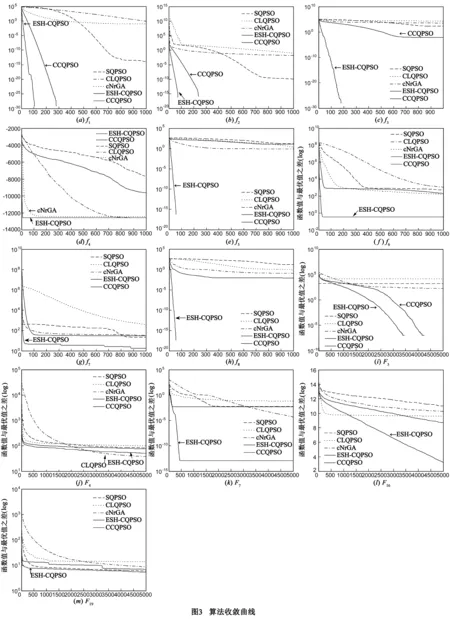
8. iff(pc(j,pkj)) 9.pij=pkj 10.Endif 11.pc=pi-b 12.End 13.pc=pi 14.End 15.End 输出:进化后的粒子群 2.4 基于演化历史信息的自变异协调量子行为粒子群优化算法 基于演化历史信息的自变异协调量子行为粒子群优化算法是一种实数编码进化算法.整个算法主要由四个部分组成,即群体初始化,进化,变异和协同选择.ESH-CQPSO算法的重点在于提高基于整个演化历史信息的自变异操作,并且通过动态协同机制选择出最优粒子. 算法4 ESH-CQPSO算法 输入:(1)给定D维最小化问题F(·);(2)搜索空间S⊂RD;(3)粒子群规模n 1. 初始化粒子群P={p1,p2,…,pn} 2. 计算每个粒子的适应度值:Fi=F(pi) 3.Pbest-i:=pj 4.Gbest:=pj∈Pwherej=argmin{F(pi) } /*BSP树初始化*/ 5. 初始化BSP树T仅包含根节点 6. fori:=1 ton 7. 将[pi,F(pi)]记录到T中 8. Nexti/*BSP树初始化结束*/ 9. While未达到终止条件 10.fori=1,2,…,n 11.pi变异yi 12.利用QPSO更新公式获得{pi1,…,pi4}[1] 13.{yi,pi1,…,pi4}根据动态协同机制产生新的下一代粒子pi 14.Nexti/*BSP树更新*/ 15.fori=1,2,…,n 16.将[pi,F(pi)]记录到T中 17.Nexti/*BSP树更新结束*/ 18.fori=1,2,…,n 19.ifF(pi) 20.Pbest-i=pi 21.Endif 22.Nexti 23.Gbest=pj∈Pwherej=argmin{F(pi) } 24.Loop 输出:最优解Gbest 3.1 测试函数 本文采用一组标准测试函数对提出的算法进行测试,验证其性能,如表1所示.其中f1(x)-f8(x)为经典测试函数.同时引入CEC14中提出的测试函数[11],F3为单峰函数,F4,F6,F7和F16为简单多峰函数,F19为混合函数. 表1 测试函数 3.2 算法设置 将提出的ESH-CQPSO算法与标准QPSO算法(SQPSO),动态协同QPSO算法(CCQPSO)[6],连续非重复访问遗传算法(cNrGA)[10],综合学习QPSO算法(CLQPSO)[12]进行性能比较. 对于SQPSO、ESH-CQPSO、CCQPSO及CLQPSO,收缩扩张因子β从1线性递减到0.5;对于cNrGA按交叉率rx=0.5进行均匀交叉;CCQPSO和CLQPSO分别按文献[6]和文献[12]设置.所有算法种群的规模设置为100,对于f1(x)-f8(x)最大迭代次数设置为1000,CEC14测试函数最大迭代次数为5000.测试函数的维数D=30,每个测试函数独立运行30次,30次实验结束后获得测试函数的最优值、均值和方差. 利用不同算法优化各测试函数30次所得到函数最优、均值和方差如表2所示.从表2可以看出来,ESH-CQPSO对于绝大部分测试函数,不论是寻优精度,还是稳定性上都能获得最佳效果.对于F4函数CLQPSO算法的均值和方差达到最优,但ESH-CQPSO算法也能获得最优值,说明对于F4函数ESH-CQPSO搜索能力还是比较强,但稳定性不够.观察表2中各算法的方差,除了F4、F16和F19以外,ESH-CQPSO算法方差都是最小的,说明对于绝大多数测试函数,ESH-CQPSO算法的稳定性也是最好的.图3(a)~图3(m)分别展示了使用5种算法求解各测试函数的收敛曲线.优化f1~f8函数时ESH-CQPSO都具有最佳寻优精度,而且收敛速度远远快于其他算法.因为ESH-CQPSO算法通过演化历史信息,找到最优子区域值后进行自适应变异操作,可以更快的搜索到最优值,而且利用协同机制可以保留最优信息,因此可以快速收敛到最优值.虽然表2显示对于f1、f2和F3,CCQPSO也能获得最优值,但从收敛曲线可以发现ESH-CQPSO的收敛速度要远快于CCQPSO.在F7和F16优化过程中,ESH-CQPSO的优化性能都要远好于另外4种算法.CLQPSO对于的F4优化较好,虽然ESH-CQPSO算法的收敛速度最快,但在搜索后期的能力稍显不足.从F19的收敛曲线可以看出,虽然各算法的收敛曲线比较相近,但ESH-CQPSO的求解能力还是最好的,收敛速度优于其他算法,表现出了最好的收敛性能,在收敛速度和精度上都获得了最佳结果.综上所述,对比各算法,ESH-CQPSO算法具有更好的收敛性能. 表2 各测试函数的优化结果 续表 为了判断ESH-CQPSO算法与其他4种算法的性能是否存在显著性差异,除了对算法的精度和收敛性进行比较外,本文还进行了Wilcoxon秩和检验[13].表3给出了ESH-CQPSO算法与其他4种算法的Wilcoxon秩和检验结果.从表3可以看出对于f1、f2和F19,ESH-CQPSO和CCQPSO的显著性差异不大,而对于F7,SQPSO也能获得和ESH-CQPSO相近的优化性能.因此对于绝大多数测试函数,ESH-CQPSO算法都能获得h=1,说明对比其他算法,ESH-CQPSO的优化性能有显著提高.由此可以看出不管是在单峰函数还是多峰函数中ESH-CQPSO算法都表现出良好的收敛性和搜索精度,优化性能显著提高. 表3 Wilcoxon秩和检验结果 早熟和多样性是QPSO算法需要解决的问题,为此本文提出了基于演化历史信息的自变异协同量子行为粒子群优化算法(ESH-CQPSO).该算法利用二维空间分割树(BSP)记录演化过程中的估计解和适应值,BSP树将连续搜索空间进行划分为不同子区域,并且产生近似适应值函数,从而获得无参的自适应变异.同时引入动态协同机制,通过更好地利用上下文信息,在协同过程中各个维度上连续动态地进行更新,最大限度地利用任何新的信息,提高变异粒子的性能,防止算法进入局部收敛,阻止早熟发生.通过实验结果表明,提出的ESH-CQPSO算法具有更好的寻优能力,收敛速度和收敛精度都有所提高,是一个可靠的有效的全局优化算法.本文提出的改进算法能在理论上证明具有一定的优越性,但在实际问题中还需要进一步进行测试,因此将ESH-CQPSO算法应用于实际工程问题是今后的研究重点,下一步研究内容就是采用一定的工程问题作为应用,如图像分割、数据聚类、生物代谢途径参数辨识等,进一步验证ESH-CQPSO算法的性能. [1]孙俊,方伟,吴小俊,等.量子行为粒子群优化:原理及其应用[M].北京:清华大学出版社,2011.31-50. [2]Kennedy J,Eberhart R C.Particle swarm optimization[A].Proc of IEEE Int.Conf.on Neural Networks[C].Perth:IEEE Press,1995.1942-1948. [3]刘朝华,李小花,章兢.精英免疫克隆选择的协同进化粒子群算法[J].电子学报,2013,14(11):2167-2173. Liu Zhao-hua,Li Xiao-hua,Zhang Jing.Co-evolutionary particle swarm optimization algorithm based on elite immune clonal selection[J].Acta Electronica Sinica,2013,14(11):2167-2173.(in Chinese) [4]Sun J,Fang W,Wu X J,Palade V,Xu W B.Quantum-behaved particle swarm optimization:analysis of individual particle behavior and parameter selection[J].Evolutionary Computation,2012,20(3):349-393. [5]Li Y,Xiang R,Jiao L,et al.An improved cooperative quantum-behaved particle swarm optimization[J].Soft Computing,2012,16(6):1061-1069. [6]Li Y,Jiao L,Shang R,et al.Dynamic-context cooperative quantum-behaved particle swarm optimization based on multilevel thresholding applied to medical image segmentation[J].Information Sciences,2015,294:408-422. [7]Glover F,Laguna M.Tabu Search[M].New York:Springer,2013.3261-3362. [8]Reynolds R G.An introduction to cultural algorithms[A].Proceedings of the Third Annual Conference on Evolutionary Programming[C].River Edge,NJ,USA :World Scientific Publishing Co,Inc,1994.131-139. [9]Farmer J D,Packard N H,Perelson A S.The immune system,adaptation,and machine learning[J].Physica D:Nonlinear Phenomena,1986,22(1):187-204. [10]Yuen S Y,Chow C K.Continuous non-revisiting genetic algorithm[A].Proceedings of IEEE Conference Evolutionary Computation[C].Trondheim:IEEE,2009.1896-1903. [11]Liang J J,Qu B Y,Suganthan P N.Problem definitions and evaluation criteria for the CEC 2014 special session and competition on single objective real-parameter numerical optimization[R].Singapore:Computational Intelligence Laboratory,Zhengzhou University,2013. [12]陈伟,周頔,孙俊,须文波.一种采用完全学习策略的量子行为粒子群优化算法[J].控制与决策,2012,27(5):719-723. Chen Wei,Zhou Di,Sun Jun,XU Wenbo.Improved quantum-behaved particle swarm optimization algorithm based on comprehensive learning strategy[J].Control and Decision,2012,27(5):719-723.(in Chinese) [13]Li Zhonghua,He Chunhui,Li Jianming,Tan Hongzhou.Adaptive hierarchical artificial immune system and its application in RFID reader collision avoidance[J].Applied Soft Computing,2014(21):119-138. 赵 吉 女,1980年9月生,江苏无锡人,博士,博士后,副教授.主要从事进化智能算法理论与应用等领域研究. E-mail:queenji97@sohu.com 傅 毅 女,1981年11月生,安徽六安人,博士,博士后,副教授.主要从事计算机数值模拟、计算生物学等领域研究. An Improved Cooperative QPSO Algorithm with Adaptive Mutation Based on Entire Search History ZHAO Ji1,2,FU Yi1,MEI Juan1 (1.ResearchCentreofEnvironmentScience&Engineering,Wuxi,Jiangsu214063,China; 2.SchoolofIoTEngineering,JiangnanUniversity,Wuxi,Jiangsu214122,China) An improved cooperative QPSO algorithm with adaptive mutation based on entire search history (ESH-CQPSO) is proposed.The proposed algorithm employs a binary space partitioning tree structure to memorize the positions and the fitness values of the evaluated solution.The cooperation mechanism between the solutions can ensure enhanced search capabilities,improve the optimize performance and prevent premature convergence.Benefiting from the space partitioning scheme,a fast fitness function approximation using the archive is obtained.The approximation is used to improve the mutation strategy in ESH-CQPSO.The resultant mutation is adaptive and parameter-less.Compared with other traditional algorithms,the experiment results on standard testing functions show that the proposed algorithm is superior regarding the optimization of multimodal and unimodal functions,with enhancement in both convergence speed and precision,which demonstrate the effectiveness of the algorithm. quantum-behaved particle swarm optimization(QPSO);entire search history;adaptive mutate;binary space partitioning;cooperative method 2015-05-21; 2015-11-12;责任编辑:梅志强 国家自然科学基金(No.61300149,No.61105128,No.61502203);江苏省青蓝工程资助(No.2012-16);江苏省自然科学基金(No.BK20131106);江南大学自主科研重点计划(No.JUSRP51410B);中国博士后科学基金(No.2014M560390) TP301.6 A 0372-2112 (2016)12-2900-08 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.12.013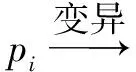
3 实验设置
4 实验结果及分析
5 结论


