基于分数阶梯度驱动的主动Demons算法研究
2017-01-10张桂梅曹红洋陈阳泉刘建新
张桂梅,曹红洋,陈阳泉,刘建新
(1.南昌航空大学航空制造工程学院,江西南昌330063;2.加州大学默塞德分校,加利福尼亚默塞德 CA95343;3.西华大学机械工程学院,四川成都 610039)
基于分数阶梯度驱动的主动Demons算法研究
张桂梅1,曹红洋1,陈阳泉2,刘建新3
(1.南昌航空大学航空制造工程学院,江西南昌330063;2.加州大学默塞德分校,加利福尼亚默塞德 CA95343;3.西华大学机械工程学院,四川成都 610039)
图像非刚性配准在计算机视觉和医学图像有着重要的作用.Demons算法被证明是解决非刚性配准的有效方法,然而存在的Demons非刚性配准算法对灰度均匀和弱纹理区域的图像配准精度低,优化易陷入局部极小导致配准速度缓慢.针对该问题,将R-L(Riemann-Liouville)分数阶微分引入到主动Demons算法中,提出了基于R-L分数阶梯度驱动的主动Demons算法.本文将R-L分数阶梯度代替传统的梯度算子,不但可以增强图像的细节信息,而且可以增强灰度均匀和弱纹理区域的梯度信息,从而提高了图像配准精度和速度.另外,通过实验给出了配准精度与R-L分数阶模板参数之间的关系,从而为模板最佳参数的选取提供了依据.尽管不同类型的图像其最佳参数是不同的,但是其最佳配准阶次一般在0~1之间.理论分析和实验结果均表明,该算法可以用于灰度均匀和弱纹理区域的图像配准,且配准精度和速度都有明显的提高,本文方法是Demons算法应用的一个重要延伸.
Riemann-Liouville;分数阶梯度;主动Demons算法;非刚性配准
1 引言
近年来,国内外不少学者研究发现分数阶微积分理论在信号分析与处理领域有着重要的应用前景.分数阶微积分理论在图像底层处理是在最近几年才引起学者关注的,并应用到图像增强,边缘检测,图像去噪和图像分割.如文献[1]提出对图像信号进行分数阶处理,既能提升信号的高频部分,又能在一定程度上非线性地加强信号的中频部分,并非线性地保留信号的低频部分和直流部分.在图像灰度均匀区域,整数阶灰度梯度必然等于0,导致纹理细节大幅线性衰减,造成图像的轮廓,纹理细节模糊不清,由于图像相邻像素之间有高度的相似性,并以复杂的纹理细节信息作为其表现形式,对图像的灰度均匀区域进行分数阶处理,分数阶微分值由对应奇异跳变处的极大值渐趋于0,其纹理细节在一定程度上得到非线性保留.文献[2]提出四元数分数阶方向微分,并将其应用于图像增强,给出四元数函数的分数阶方向微分的定义和计算方法,继而推导出沿八个方向的四元数分数阶方向导数的数值计算模板.该方法应用于图像增强能使图像边缘明显突出、纹理更加清晰和图像平滑区域信息得以非线性保留.文献[3]提出一种分数阶微分的边缘检测算子:CRONE,详细地分析了0~1和1~2阶次范围的微分算子的边缘检测效果.文献[4]提出基于Riemann-Liouville分数阶微分的边缘检测方法,能够检测到灰度发生急剧变化的非线性边缘,选择适当阶次可以增强图像的边缘和纹理信息,同时保留图像的平滑区域信息,对噪声具有较强的鲁棒性.文献[5]针对常用的边缘梯度检测方法难以有效提取类似于分形纹理结构的复杂图像边缘问题,提出一种基于Grumwald-Letnikov (G-L)分数阶微分的图像边缘检测方法,该算子对被噪声严重污染的具有复杂边缘细节的图像具有较好的边缘细节检测能力,获得了更好的视觉效果.文献[6]将分数阶积分理论引入到图像去噪,通过设定较小的分数阶阶次来构建相应的图像去噪掩模,该方法不仅比传统的去噪方法提高图像信噪比,而且能够更好的保留图像的边缘和纹理等细节.文献[7]将分数阶微分应用到图像分割领域,实验结果表明该方法对纹理丰富的图像获得很好的分割结果.受以上文献的启发,分数阶微分可以增强图像的纹理细节,又能保留图像的平滑区域信息,本文考虑将分数阶微积分理论应用到图像配准领域.
图像的配准[8]是指在不同时段、不同视角和不同传感器下拍摄的两幅或多幅图像间的几何变换关系的处理技术,它是图像处理和计算机视觉领域比较基础的技术,被广泛应用于包括图像融合、目标定位、图像拼接、疾病的精确诊断等方面,因而提高图像配准的精度和效率是十分迫切的.目前,图像的配准技术大致可分为两大类:刚性配准和非刚性配准.刚性配准[9]是假设图像的形变是刚性的,只有旋转,平移运动,刚性配准只适用于不存在变形的配准,但是现实中图像形变大多是非刚性,需要用非刚性的配准算法来解决图像局部或全局变形精确配准问题,如大变形图像的配准和不同个体之间的配准等都需要用到图像非刚性配准方法.目前的非刚性配准方法有基于B样条的弹性配准[10],该方法以三次B样条为弹性形变模型,每一段B样条曲线只和相邻的4个控制点有关,改变任意一个控制点也只会影响与它相关的4个B样条曲线段,因而每一个控制点都对变换有局部性的影响,具有较强的抵御杂点影响的能力,适用于局部形变.文献[11]提出基于扩散理论的Demons的光流场模型,其基本思想是将配准看作是浮动图像像素在参考图像像素灰度梯度信息驱动下向参考图像逐步扩散的过程.但是,以参考图像的梯度信息作为配准驱动力的Demons算法对灰度均匀的区域无效和优化容易陷入极小.文献[12]提出允许参考图像和浮动图像的梯度共同驱动像素点向着对方对应的像素点移动的主动Demons算法,可以处理大变形图像配准问题,即使参考图像的梯度很小时,也能得到较高的配准精度.文献[13]提出了微分同胚Log Demons算法,基本思想是在微分同胚空间(李群)来优化目标能量函数,确保变形场的可逆性,可微性和空间点的一一对应,阻止变形空间的折叠.文献[14]提出新的基于局部互相关相似性测度的微分同胚LCC Demons算法,该算法可以削弱灰度偏差对医学图像配准的影响,具有更高的配准精度.但是文献[11~14]的Demons算法驱动内力来自于图像的灰度梯度,对图像的灰度均匀的区域无效和优化容易陷入极小.针对该问题,本文将R-L分数阶梯度应用到Demons算法中,以提高Demons算法的配准精度和配准速度.
本文的主要内容为:首先详细的介绍了分数阶微积分理论在图像增强,边缘检测,图像去噪和图像分割的研究现状,而且对Demons配准算法的局限性进行了详细的分析.其次回顾了Demons和主动Demons算法的原理.再次介绍R-L分数阶微分掩模的构造,并且用实验去验证R-L分数阶的优势,即R-L分数阶微分不但可增强图像的细节信息,而且可增强灰度均匀和弱纹理区域的梯度.然后通过实验给出了配准精度与模板参数(阶次和模板宽度)之间的关系,从而为模板最佳参数的选取提供了依据,并且从理论和实验两方面分析了分数阶微分最佳阶次的选择区间为0~1.最后用综合图像、标准库图像和真实图像实验证明R-L分数阶微分不但提高了图像配准的精度而且也加快了图像配准速度.
2 基本理论
2.1 原始Demons算法
1998年,Thirion提出Demons[11]算法的灵感源自于19世纪Maxwell为了解决热动力学难题而提出的一种假设.其假设参考图像和浮动图像是连续运动图像序列中的任意两帧图像,要完成两帧图像间的配准,其实就是需要找到驱动力F使得浮动图像M的每一个像素点向着参考图像S对应的像素点移动.整个过程可以看做光流运动,也可以看做位移形变场的移动.光流场理论假设浮动图像的灰度不变,是个常数值C.即
I(x(t),y(t),t)=C
I(x(t0),y(t0),t0)=M
U·▽S=M-S
(1)
由式(1)可知,在t0时刻,一帧图像为浮动图像M,另一帧图像为参考图像S.对I(x(t),y(t),t)微分得:
(2)
将上式化简为:
U·▽S=M-S
(3)
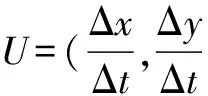
(4)
然而,静态图像有些区域灰度均匀(即这些区域的灰度值相等,导致静态图像的灰度梯度为0,从而造成式(4)的值十分不稳定).为了解决这个问题,在式(4)的分母上再加入一个分量,以减少不稳定现象.
(5)
2.2 主动Demons配准算法
经典Demons算法的缺点是变形力仅仅来自于静态图像的梯度,而文献[12]将变形力来自参考图像和浮动图像,允许像素进行双向扩散,提出了主动Demons算法.该算法允许参考图像和浮动图像的梯度共同驱动像素点向着对方对应的像素点移动,因而可以处理大变形图像配准问题,即使参考图像的梯度很小,也能获得较高的配准精度.主动Demons的驱动力公式为:
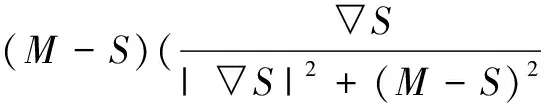
(6)
主动Demons算法不仅能够配准较大形变的图像,而且能够加快配准收敛速度.在式(6)中加入均化系数β,调整驱动力的强度.因而变成:
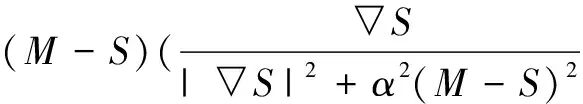
(7)
但是其梯度是gradient函数,为灰度中值差分:
▽Sx(i,j)=[S(i+1,j)-S(i-1,j)]/2 ▽Sy(i,j)=[S(i+1,j)-S(i-1,j)]/2
该梯度算子对灰度均匀和弱纹理区域的图像配准精度低,本文尝试用R-L分数阶梯度代替基于gradient函数的梯度.
3 R-L分数阶梯度驱动的主动Demons算法
常用的分数阶微积分算子有三种,分别为Caputo、R-L和G-L.其中Caputo、R-L都是对G-L的改进,在一定条件下,三种微积分可以相互转换.分数阶微积分Caputo定义适用于分数阶微分方程的初边值的分析,因而多应用在工程领域.而分数阶微积分的R-L定义和G-L定义在数值运算时都可以转化为卷积运算形式,故适合应用在图像处理领域.但是R-L定义具有定义清晰,计算简单的优点,因此本文从R-L定义出发,对主动Demons算法进行改进,用于对图像的非刚性配准.
3.1 R-L分数阶微分掩模的构造
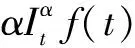
(8)
式中:Γ(α)是gamma函数,其定义为:
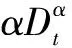
(9)
由卷积定理,式(8)可以重新写成:
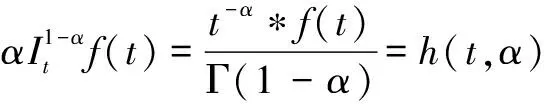
(10)
其中,*是卷积符号.由式(10)将式(9)写成:
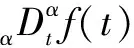
(11)
将式(11)扩展到二维空间,则形成:
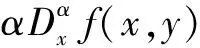
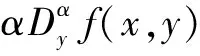
(12)
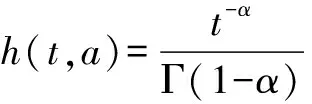
(13)
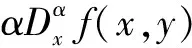
(14)
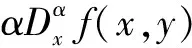
(15)
其中xM=-K,-K+1,…,K,yN=-L,-L+1,…,L.Hx(x,y,α)和Hy(x,y,α)是(2K+1)×(2L+1)的微分掩模算子.当α取0.5时,可得到5×5的掩模分别为:
Hx(x,y,0.5)=

Hy(x,y,0.5)=[Hx(x,y,0.5)]T
(16)
3.2 R-L分数阶微分的实验验证
为了证明R-L分数阶微分算子在图像配准过程中可以增强提取梯度信息,我们选择整个棋盘格图像和其局部小区域(ROI)做验证试验.图1是完整的棋盘格,用gradient函数和R-L分数阶分别计算其梯度,为了便于观察效果,同时放大2.5倍,并矢量化.对比二个梯度矢量场,我们发现基于gradient函数矢量场比R-L分数阶(0.5阶)梯度矢量场稀疏,这说明基于gradient函数没有将某个区域的梯度提取出来.为了清楚哪些区域的梯度没有被提取出来,我们选择感兴趣的局部区域(ROI)做验证,在图2中,我们可以清晰地看出基于0.5阶的分数阶梯度可以将红色方框的梯度提取出来.但是基于gradient的梯度算子,却没有将中间方格的边缘部分的梯度提取出来.这说明R-L分数阶微分能够增强图像灰度变化较大的梯度信息.
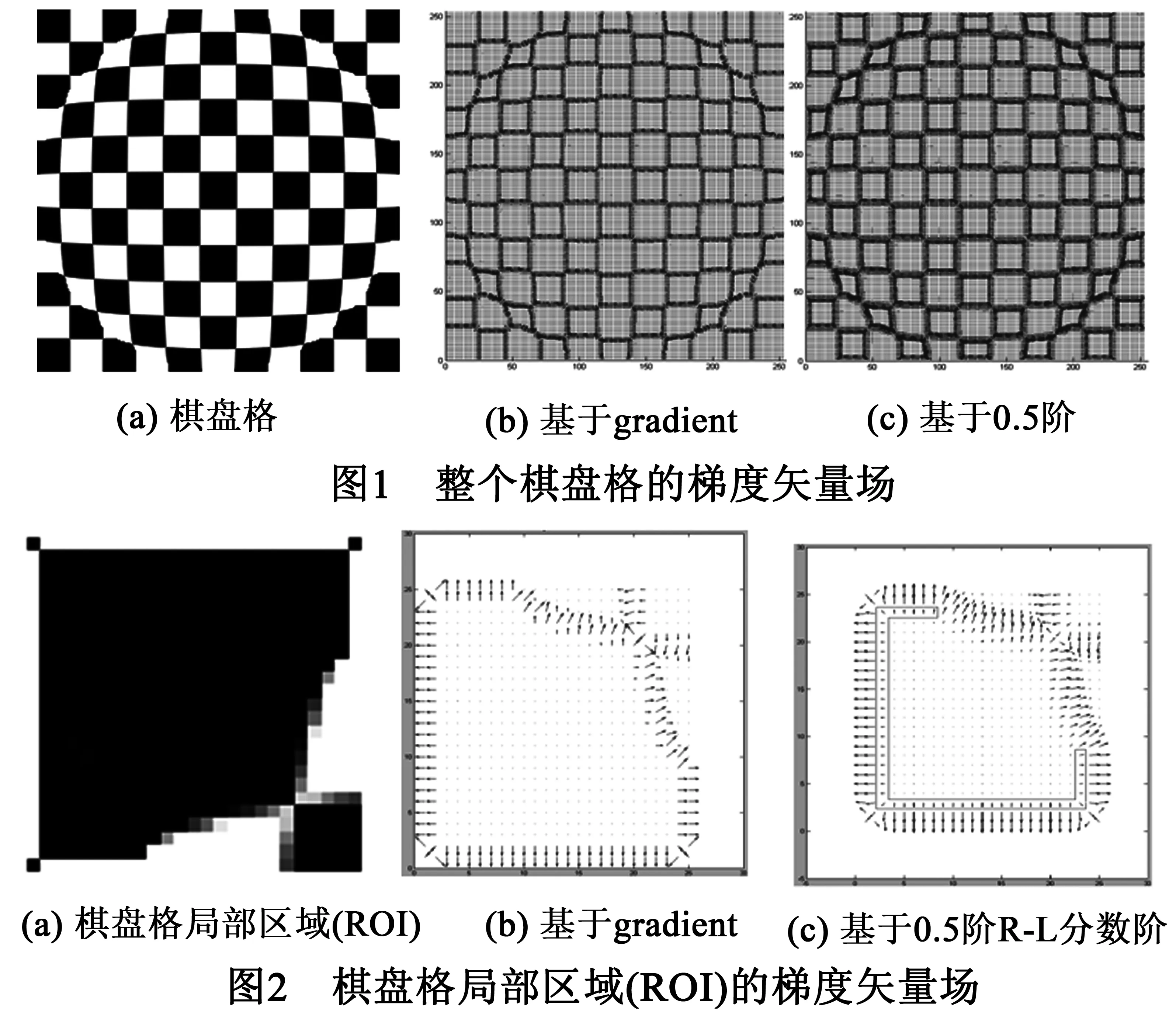
3.3 算法流程
上述实验证明,基于R-L的分数阶梯度可以增强灰度均匀区域的梯度信息,因而将R-L分数阶梯度去代替传统的梯度算子.将式(7)改为:
(17)
在R-L分数阶梯度和图像的灰度差的共同驱动下,完成图像间的配准.该算法的流程如下:
(1)首先计算图像像素每一个像素点i在坐标p位移形变场ui(p),得到该点的位移更新ui(p).
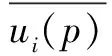
(4)对图像像素点进行线性插值Ti+1,从而完成图像配准.
4 分数阶微分掩模参数的选取
4.1 精度评价准则
图像配准常用的评价标准为客观评价和主观评价.其中主观评价即是我们肉眼观察配准后图像与原始图像的相似程度以及从二者的差值图像黑色区域所占图像的大小.而客观评价为配准后的图像和原始图像的灰度均方误差MSE(Mean Square Error)[15].
基于灰度的均方误差表示如下:
(8)
其中,F是参考图像,F′是配准算法得到的配准图像,n表示像素的个数.该测度最理想情况下应该为零,表示两幅图像同一位置的两个对应像素应该有相同的灰度值.MSE作为相似性测度时,测度最理想情况为零,但在实际过程中,该测度并不为零.
4.2 微分掩模的参数分析
对某一个平方可积的信号s(t)∈L2(R),其α分数阶微积分为:
(9)
则其Fourier变换为
(20)
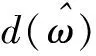
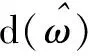
(21)
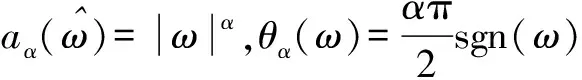
根据式(21)绘制分数阶微积分的幅频特性曲线,如图3所示,当阶次小于0时,为分数阶积分;大于0时,相当于分数阶微分;等于0时,既不积分也不微分.当选用阶次小于0的分数阶积分算子,信号的高频部分被极大的衰减,一般用于图像去噪处理.当选用阶次在1~2之间的分数阶微分算子时,能极大的增强信号的高频部分,且随着阶次和频率的增加呈非线性增加,而且对信号的低频极大地衰减,但也可能获得无关内部纹理细节信息.当选用阶次在0~1之间的分数阶微分算子时,高频信号被增强的程度不如阶次在1~2之间的分数阶微分算子,但是其中频信号得到较大的增强,低频信号没有极大的衰减,反而得到非线性保留.
总之,根据图像处理关注的目标不同,我们选用不同范围的阶次.在图像处理中,低频成分对应图像的平滑区域,中频部分对应图像的纹理细节,高频部分对应图像的轮廓和噪声.而Demons算法对图像灰度均匀区域和弱纹理区域的配准精度低,增强这些区域的梯度信息,需要提高其中频部分和低频部分,因而需要选用0~1的分数阶微分算子配准精度更高.
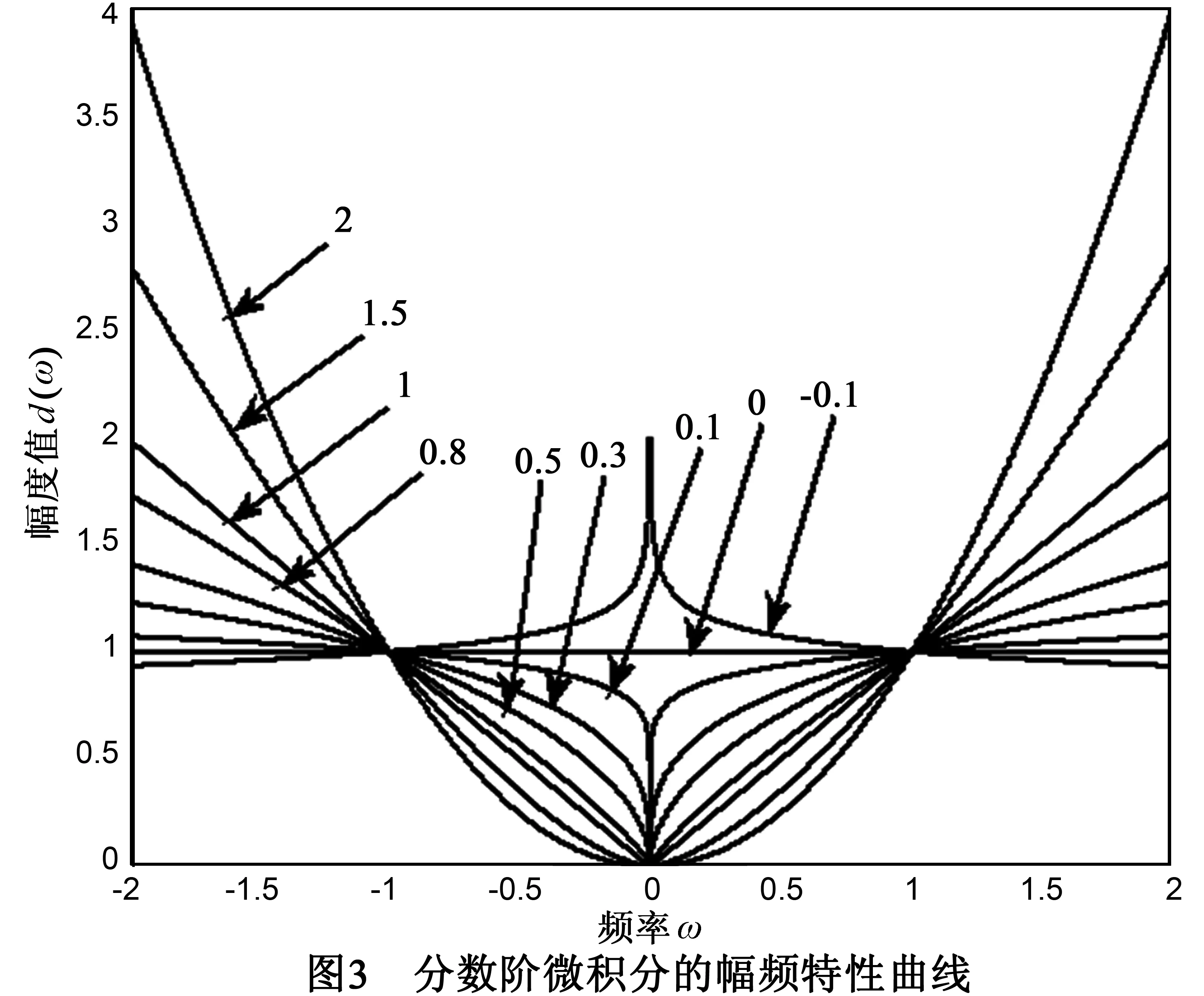
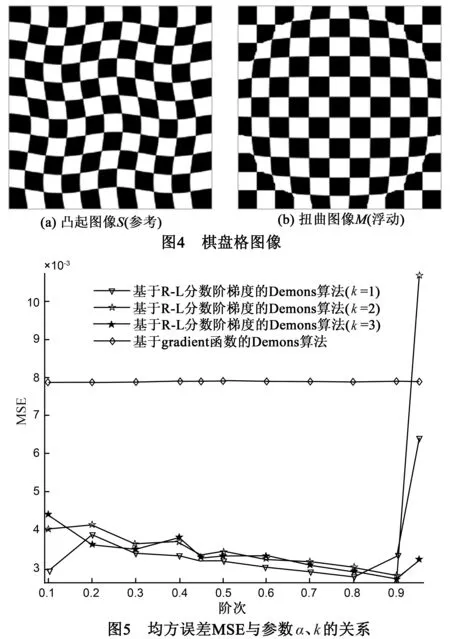
为了得到最佳的模板参数,我们进一步进行实验,依据前面提到的灰度均方误差MSE来分析模板的参数α,K对配准精度的影响.选取如图4所示的棋盘格图像进行实验验证,图4中的S和M图像是程序生成的正常棋盘格分别挤压和扭曲生成凸起和扭曲的棋盘格图像.据上面的分析,分别选取α=(0~1)测试不同阶次下的图像配准精度,Hx(x,y,α)和Hy(x,y,α)同时是(2K+1)×(2L+1)的微分掩模算子,一般情况下K=L,当分别取1,2,3时,对应的微分掩模算子的大小为3×3,5×5,7×7.首先固定模板宽度(K分别取1、2、3),调整不同的阶次进行实验,并与基于gradient函数的主动Demons算法进行比较,得到如图5所示关系曲线图.该图表明基于R-L分数阶梯度驱动的主动Demons算法的配准精度远远超出原始的主动Demons算法.该实验同时也展示了灰度均方差MSE在基于R-L分数梯度的Demons算法中随着不同阶次α和掩模宽度K的配准精度变化关系.即随着α在(0~1)区间不断增加,其配准精度基本上呈上升趋势,当阶次达到0.95后,图像灰度均匀区域的低频信号被极大地衰减,中频信号也被部分削弱,导致图像的纹理细节模糊不清,使得图像配准精度极大的降低.图5中基于R-L分数阶的每条曲线都会出现一个最低点,该点所对应的横坐标即为最佳的阶次α.当α=0.9,K=3时其配准精度为0.0027,达到最佳水准.该实验进一步证明R-L分数阶的最佳阶次范围在0~1之间,但是不同图像的最佳配准精度,是需要不断测试出最佳的α,K参数.
5 实验结果与分析
本文实验所采用的计算机环境为:实验机器配置Intel(R) Core(TM) 2 Quad CPU,Q8400,2.66GHz,3.25GB内存,操作系统为Windows XP,程序采用Matlab2010a实现,图像均为灰色图像,并将灰度归一化.本文选择综合图像,标准库图像和真实图像,即三种不同类型图像进行测试.
5.1 综合图像实验
本次实验选用如图4所示的图像进行配准实验.结果如图6所示,从图6我们可以清晰地发现基于gradient梯度函数的Demons的图像配准生成的配准图像S#的圆圈标注的区域是图像灰度均匀区域的交叉处,此处棋盘格的拐角处依然发生严重变形.而基于0.5阶R-L分数阶梯度的Demons图像配准图像算法生成的图像S&就可以将扭曲的棋盘格大致校正到原始凸起的棋盘格形状,图像S&和凸起的图像S更相似.若是理想的完全配准,其差值图像的灰度值是0,其区域颜色应该完全是黑色的.|S#-S|的差值图像中大部分区域是黑色的,但是有两区域是白色的,那么说明该区域的配准精度较差.而|S&-S|的差值图像整个区域基本是黑色的,那么说明其配准效果很好.其余是配准图像与原始输入图像S的差值图像.从这些差值图像可以得出不同α,K参数的基于R-L分数梯度的Demons算法远远胜于原始的Demons算法.由上节实验结果可知当α=0.9时,K=3时配准精度为0.0027,达到最佳效果.

5.2 标准库图像实验
为了增强算法说服力,本文选用标准库图像(Lena)作为参考图像,并将Lena人工变形,获得变形的浮动图像.经过实验测试其最佳配准参数为:α=0.5,K=3.
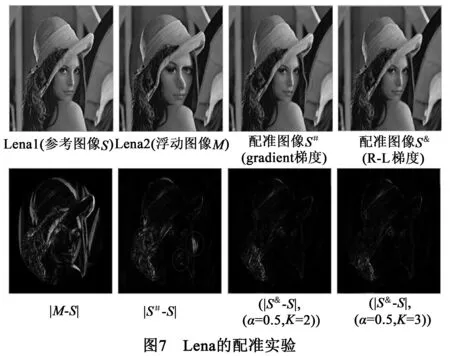
图7中,Lena1和Lena2分别是参考图像和浮动图像,Lena2的鼻子和眼睛发生局部扭曲,而S#是原始Demons算法生成的配准图像,S&是基于R-L分数阶梯度的Demons算法生成的配准图像(α=0.5,K=3).S#图像中明显观察出圆区域发生了明显的突起,而对照Lena1图像的该区域没有突起的形状,对应的S&的该区域也没有突起,则说明了原始的Demons算法的局限性.|M-S|是未配准的差值图像,对比图7第二行的其余三个差值图像,在α=0.5,K=3的差值图像,其黑色区域所占的区域最大,则佐证了基于R-L分数阶梯度的Demons算法可以增强在纹理丰富区域提取梯度的能力,提高驱动图像像素点移动的驱动力,从而提高配准的精度.在α=0.5,K=3生成的图像灰度均方差6.86×10-4,而Demons算法生成的图像灰度均方差为0.0017,提高了59.64%.
5.3 真实图像实验
本文选择真实的颅脑MRI矢状图像(T1加权),图8中的Brain1和Brain2为参考图像和浮动图像,我们肉眼几乎观察不出二幅图像之间的变形,但是我们从未配准图像的差分图像可以清晰看出,还是有轻微的局部变形.原始Demons算法配准后我们发现生成的差值图像的脑垂体区域依然有大量白色区域.而本文算法生成的差值图像(α=0.5,K=2)和差值图像(α=0.5,K=3)的白色区域有很大减少.当α=0.5,K=3时,本文图像配准的灰度均方差是2.89×10-5,而Demons算法配准的灰度均方差为8.16×10-5,提高了64.58%.灰度均方差如表一所示.

表1 灰度均方差
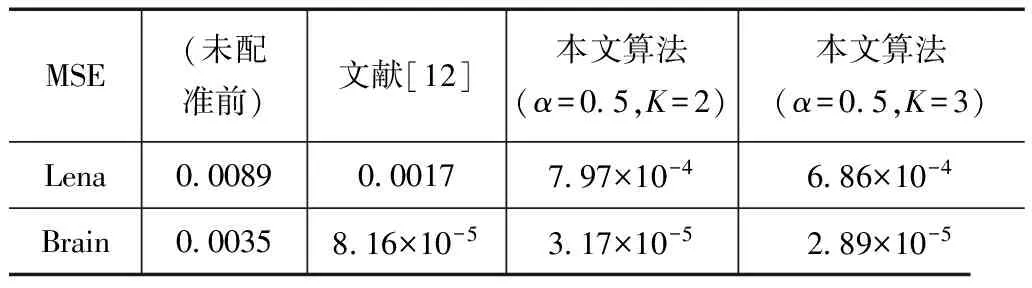
MSE(未配准前)文献[12]本文算法(α=05,K=2)本文算法(α=05,K=3)Lena0008900017797×10-4686×10-4Brain00035816×10-5317×10-5289×10-5
5.4 配准时间
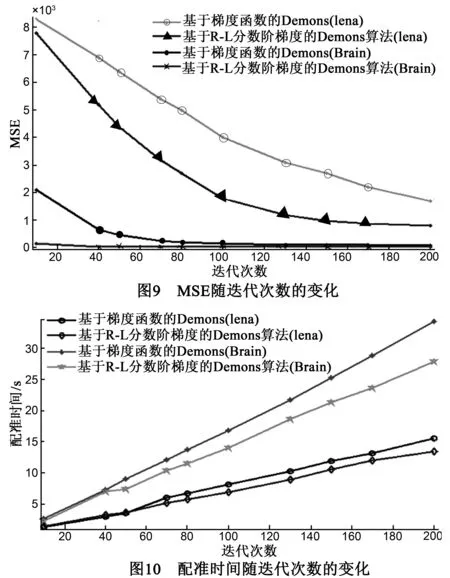
原始Demons算法在灰度均匀区域的梯度接近于零,使得驱动力十分不稳定,优化陷入局部极小,造成收敛速度减缓,从而增长图像配准时间.而基于R-L的Demons算法可以增强灰度均匀和弱纹理区域的梯度,加大梯度驱动力,使得收敛速度更快,从而减少图像配准时间.图9中我们发现原始的Demons算法的Lena灰度灰度均方差在迭代200次的依然没有收敛,Brain在迭代100次收敛,而本文算法Lena的灰度均方差在迭代170次,Brain在迭代40次收敛,本文的收敛速度更快,配准时间更短.图10中,同样迭代200次,多次测试取平均值,原始Demons算法Lena和Brain配准时间为15.55秒,34.35秒,而本文算法的配准时间为13.42秒,27.89秒.
6 结论
将R-L分数阶微分引入到主动Demons算法中,能解决灰度均匀和弱纹理区域的图像配准.一方面,R-L分数阶微分不但可以增强图像的细节信息,而且可以增强灰度均匀和弱纹理区域的梯度信息,因此图像配准的精度能得到提高;另一方面,原始主动Demons算法在灰度均匀区域的梯度接近于0,使得驱动力不稳定,优化易陷入局部极小,造成收敛速度减缓,而新提出的配准算法可以增强灰度均匀和弱纹理区域的梯度,从而加大了梯度驱动力,使得收敛速度更快,因此能提高图像配准的效率.另外,通过实验给出了配准精度与R-L分数阶模板参数之间的关系,从而为模板最佳参数的选取提供了依据.当然不同类型图像的配准,其最佳参数是不同的,但是其最佳配准阶次在0~1之间.理论分析和实验结果均表明,本文的方法可以用于灰度均匀和弱纹理区域的非刚性图像配准,并能提高配准的精度和效率,是主动Demons算法应用的一个重要延伸.
不同图像的最佳配准精度,其阶次是需要不断测试,因而是比较耗时和费力的.今后可以研究自适应R-L分数阶梯度驱动的图像非刚性配准算法.此外本文的分数微分掩模是二维的,要完成三维图像的配准,还需将其扩展到三维空间.
[1]蒲亦非,王卫星.数字图像的分数阶微分掩模及其数值运算规则[J].自动化学报,2008,33(11):1128-1135. Pu Yi-fei,Wang Wei-xing.Fractional differential masks of digital image and their numerical Implementation algorithms[J].Acta Automatica Sinica,2007,33(11):1128-1135.(in Chinese)
[2]高朝邦,周激流.基于四元数分数阶方向微分的图像增强[J].自动化学报,2011,37(2):150-159. Gao Chao-bang,Zhou Ji-liu.Image enhancement based on quaternion fractional directional differentiation[J].Acta Automatica Sinica,2011,37(2):150-159.(in Chinese)
[3]Mathieu B,Melchior P,Oustaloup A,et al.Fractional differentiation for edge detection[J].Signal Processing,2003,83(11):2421-2432.
[4]Chen,Da-li,Xue Ding-yu,Chen Yang-quan.Fractional differentiation-based approach for robust image edge detection[A].Proceedings of 2012 Fractional Derivative and Applications(FDA2012)[C].Nanjing,China:Hehai University Press,2012.5-17.
[5]陈青,刘金平,唐朝晖,等.基于分数阶微分的图像边缘细节检测与提取[J].电子学报,2013,41(10):1873-1880. Chen Qing,Liu Jin-ping,Tang Zhao-hui,et al.Detection and extraction of image edge curves and detailed features using fractional differentiation[J].Acta Electronica Sinica,2013,41(10):1873-1880.(in Chinese)
[6]黄果,蒲亦非,陈庆利,等.基于分数阶积分的图像去噪[J] 系统工程与电子技术,2011,33(4):925-932. Huang Guo,Pu Yi-fei,Chen Qian-li,et al.Research on image denoising based on fractional order integral [J].Systems Engineering and Electronics,2011,33(4):925-932.(in Chinese)
[7]Pu Y-F,Zhou J-L.A novel approach for multi-scale texture segmentation based on fractional differential[J].International Journal of Computer Mathematics,2011,88(1):58-78.
[8]Brown L G.A survey of image registration techniques[J].ACM Computing Surveys (CSUR),1992,24(4):326-376.
[9]张桂梅,江少波,储珺.基于弦高点和遗传算法的仿射配准[J].自动化学报,2013,39(9):1447-1457. Zhang Gui-mei,Jiang Shao-bo,Chu Jun.Affine registration based on chord height point and genetic algorithm[J].Acta Automatica Sinica,2013,39(9):1447-1457.(in Chinese)
[10]彭晓明,陈武凡,马茜.基于 B 样条的弹性点配准方法[J].中国图象图形学报,2007,12(6):1079-1085. Peng Xiao-ming,Chen Wu-fan,Ma Qian.Elastic point registration method based on B-splines[J].Journal of Image and Graphics,2007,12(6):1079?1085.(in Chinese)
[11]Thirion J P.Image match ing as a diffusion process:an analogy with Maxwell′s demons[J].Medical Image Analysis,1998,2(3):243-260.
[12]Wang H,Dong L,O′Daniel J,et al.Validation of an accelerated′demons′ algorithm for deformable image registration in radiation therapy[J].Physics in Medicine and Biology,2005,50(12):2887.
[13]Vercauteren,Tom,et al.Symmetric log-Demons diffeomorphic registration:A demons-based approach[A].Medical Image Computing and Computer-Assisted Intervention-MICCAI 2008[C].New York,USA:Springer Berlin Heidelberg,2008.754-761.
[14]Lorenzi M,Ayache N,Frisoni G B,et al.LCC-Demons:A robust and accurate symmetric diffeomorphic registration algorithm[J].NeuroImage,2013,81(3):470-483.
[15]Vercauteren T,Pennec X,Perchant A,et al.Non-parametric diffeomorphic image registration with the demos algorithm[A].Medical Image Computing and Computer-Assisted Intervention-MICCAI 2007[C].Brisbane,Australia:Springer Berlin Heidelberg,2007.319-326.

张桂梅 女,1970年生于江西临川,2006年获西北工业大学博士学位,现为南昌航空大学航空制造工程学院教授.主要研究方向为图像处理,计算机视觉与模式识别等.
E-mail:guimei.zh@163.com

曹红洋 男,1988年生于安徽合肥,2012年进入南昌航空大学,现为南昌航空大学航空制造工程学院硕士研究生.研究方向为图像配准与目标检测与识别.
E-mail:caohongyang123456@163.com

陈阳泉 男,1966年生于江苏南京,1998年获新加波南洋理工大学博士学位,现为加州大学Merced分校教授.主要研究方向为分数阶理论及其应用等.
E-mail:ychen53@ucmerced.edu

刘建新 男,1969年生于湖北红安,1997年获重庆大学博士学位,现为西华大学机械工程学院教授.主要研究方向为智能控制,机器人技术与视觉伺服等.
E-mail:jamson-liu@163.com
Research on Active Demons Based on Fractional Differentiation Gradient Driving
ZHANG Gui-mei1,CAO Hong-yang1,CHEN Yang-quan2,LIU Jian-xin3
(1.SchoolofAeronauticalManufacturingEngineering,NanchangHangkongUniversity,Nanchang,Jiangxi330063,China; 2.Mechatronics,EmbeddedSystemsandAutomationLab,SchoolofEngineering,UniversityofCalifornia,Merced,CaliforniaCA95343,USA; 3.SchoolofMechanicalEngineering,XihuaUniversity,Chengdu,Sichuan610039,China)
Non-rigid image registration plays an important role in computer vision and medical image.Demons algorithm has been proved to be effective for non-rigid image registration;however,the existing Demons algorithms are limited in registration image for intensity uniformity or weak textile region,which always results in low registration accuracy and efficiency.Aiming at the problem,this paper applies R-L(Riemann-Liouville) fractional differentiation to active Demons,and proposes a new image registration based on fractional differentiation active Demons.In this paper we calculate image gradient using R-L fractional differentiation instead of the traditional gradient function,not only detail feature is strengthened but also image gradient of intensity uniformity and weak textile area is enhanced,thus registration accuracy and efficiency are improved.Additionally,we give the relation curve between registration accuracy and mask parameters,which can guide one to select optimal parameters.Though optimal parameter (order) is different for different images,it is proved the optimal interval is between 0~1.Theoretical analysis and experiment results show the effectiveness of the proposed method.It is a significant extension of Demons algorithm.
Riemann-Liouville;fractional order gradient;active Demons algorithm;non-rigid registration
2015-02-03;
2015-05-17;责任编辑:梅志强
国家自然科学基金(No.61462065);江西省自然科学基金(No.2015BAB207036)
TP391
A
0372-2112 (2016)12-2834-08
��学报URL:http://www.ejournal.org.cn
10.3969/j.issn.0372-2112.2016.12.004
