改进的基于故障特征平面的双星故障识别算法

武永明，李 魁,2，吕妍红，王灵草

(1.北京航空航天大学仪器科学与光电工程学院，北京 100191； 2.北京航空航天大学电子信息工程学院，北京 100191)

改进的基于故障特征平面的双星故障识别算法

武永明1，李 魁1,2，吕妍红1，王灵草1

(1.北京航空航天大学仪器科学与光电工程学院，北京 100191； 2.北京航空航天大学电子信息工程学院，北京 100191)

针对基于识别门限的奇偶矢量法等双星故障识别算法存在较大误警率、漏检率以及故障偏差抵消致使双星故障正确识别率较低的问题，提出了一种改进的用于双星故障识别的接收机自主完好性监测算法.在奇偶矢量法的基础上，构造故障特征平面和改进奇偶矢量，分析二者之间的几何特征与卫星故障的关系，并设计相应算法识别故障卫星.该算法不受识别门限的影响，避免了由识别门限引起的识别率较低的不足.半物理仿真结果显示：改进后的算法故障识别率达到90%以上，与直接利用奇偶矢量法相比，可以显著提高双星故障识别率.

自主完好性监测；奇偶矢量；故障特征平面；故障识别

1 引言

目前卫星完好性监测主要分为系统级完好性监测和用户级完好性监测.系统级监测主要包括星基增强系统(Satellite Based Augmentation System，SBAS)和地基增强系统(Ground Based Augmentation System，GBAS)；用户级监测主要是指卫星接收机完好性监测(Receiver Autonomous Integrity Monitoring，RAIM).用户端自主完好性监测技术利用GNSS卫星的冗余观测信息，对多个导航解进行一致性检验来实现卫星完好性监测，其优点在于自主性强、对卫星故障反应迅速且自动，无需外界干预，因而逐渐成为完好性监测算法的主要研究方向.而如何有效地识别卫星故障一直是RAIM算法中的研究热点之一.早期关于RAIM的研究大多集中在单星故障,随着可用于定位的卫星星座的增多，多颗卫星同时发生故障的概率特别是两颗卫星同时发生故障的概率不能再被忽略[1～3].

RAIM算法包括两大类：一类是基于卡尔曼滤波产生的新息进行故障识别的算法[4～6]，另一类是利用当前伪距观测量的“快照(snapshot)”算法.文献[6]提出利用卡尔曼滤波进行故障监测，该算法通过结合时域与集合一致性检测的互补特性，提高了多故障识别率，但其故障识别性能依赖于先验误差估计的准确性且检测速度较慢.“快照(snapshot)”算法由于反应速度快、容易实现等优点，得到了广泛的使用，这类算法目前主要有奇偶矢量法、最小二乘残差法等[7～10].文献[7]提出了重构奇偶矢量法用于双星故障识别，极大提高了故障识别的性能.但其基于识别门限进行故障识别，且利用了调节系数对识别门限进行调整以防止漏检，当可视卫星数目较多时，调节系数如何设置又成为另一个需要解决的问题；文献[10]提出利用故障特征平面与奇偶矢量的几何关系来进行故障识别，但算法没有考虑故障偏差抵消对双星故障识别率的影响.

本文首先介绍了基于奇偶矢量的双星故障识别算法，分析了传统算法存在的不足，然后提出了一种改进的“快照(snapshot)”算法，即通过改进奇偶矢量以及判断奇偶矢量与构造的故障特征平面之间的几何特征来识别双星故障，有效提高了双星故障的识别能力.

2 双星故障识别算法简介

由卫星定位原理得到的卫星观测方程如下：

y=Hx+b+e

(1)

其中，y是观测伪距与近似计算伪距之差，y∈Rn(n是可观测卫星数)；H是由伪距观测方程线性化得到的系数矩阵，H∈Rn×m；x是待求参数矢量，x∈Rm(单星座定位时m=4，每多1个星座，m加1)；b表示卫星故障向量，当没有卫星故障时b=0，否则b不为0；e是伪距测量噪声向量且e∈Rn，ei是均值为0的高斯白噪声，ei～N(0,σ2),σ2表示伪距测量方差.

对系数矩阵H进行QR分解，得到

y=QRx+b+e

(2)

其中：Q是n×n维正交矩阵，R为n×m维上三角阵.给式(2)两边左乘QT,并将QT和R分别表示为[QxQp]T及[Rx0]T，其中，Qx为QT的前m行，Qp为其余n-m行，Rx为R的前m行，则有

(3)

(4)

由于QpH=0，所以

p=Qpy=Qp(Hx+b+e)=Qp(b+e)

(5)

由式(5)可以看出，奇偶矢量p仅与测量噪声和卫星故障有关[11,12].奇偶矢量法正是根据奇偶矢量p在有故障和无故障情况下表现的不一致性进行故障的检测和识别.

当导航系统正常工作时，伪距噪声向量e中各个分量是相互独立的正态分布随机误差，均值为0，方差为σ2.为方便讨论，暂时忽略观测噪声的影响，首先考虑单星故障的情况.假设第i颗卫星发生故障，则卫星故障向量b中元素bi不为0，由式(5)可以得到

p=Qp(:,i)bi

(6)

从式(6)可以看出，发生单星故障时，奇偶矢量p与故障特征向量Qp(:,i)成比例关系.类似地，不考虑观测噪声，假设卫星i和卫星j发生故障，可以得到

p=Qp(:,i)bi+Qp(:,j)bj

(7)

从式(7)可以看出出现双星故障时，奇偶矢量p不再与Qp的任一列向量成比例，而是两故障特征向量Qp(:,i)和Qp(:,j)的线性组合.将p投影到Qp的每一列并进行归一化，可以得到检测统计量ri为：

(8)

给定误警率α，可以得到故障识别准则：若ri>T1-α/2，当前特定卫星有故障；否则无故障.T1-α/2是正态分布N(0,σ2)的1-α/2分位点.

3 双星故障识别算法的不足

从第2节的分析可以看出，以上双星故障识别算法在利用识别门限进行故障识别时，有以下2个不足.

3.1 存在较大误警和漏检

如图1所示，图中f1和f2、f3和f4代表卫星故障特征向量，T代表识别门限.从图1中可以看出，当两个故障特征向量的模已经达到识别门限时，其和向量M的模还小于识别门限，从而引起漏检；两个故障特征向量的模小于识别门限，但其和向量N的模已经达到识别门限，从而引起误警.

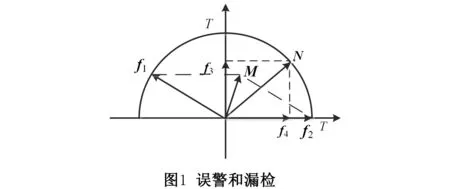
文献[7]分析了产生漏检的原因，并采取了重构奇偶矢量结合符号判断的方法避免漏检.但是其构造的对卫星故障敏感的奇偶矢量以忽略观测噪声为前提，且并非最优，为了补偿观测噪声的影响，其通过调节系数调整识别门限以防止漏检，这使得算法的效率有所降低，调节系数如何选取也成为另一个需要解决的问题.

3.2 存在故障偏差抵消

假设卫星i和卫星j发生故障，即向量b中bi和bj不为0，利用奇偶矢量法得到分别对卫星i和卫星j故障敏感的故障特征向量qi和qj.忽略观测噪声的影响，可以得到对双星故障敏感的奇偶矢量p：

p=qibi+qjbj

(9)

若式(6)中bi·bj<0且qi(n)·qj(n)>0，或bi·bj>0且qi(n)·qj(n)<0，则p(n)有可能为0或接近于0.此时发生了故障偏差抵消的情况，导致有无故障时的奇偶矢量p都可能为0，增大了故障检测和识别的难度.

4 改进的双星故障识别算法

为了减小以上不足带来的影响，本节将基于奇偶矢量法提出改善的用于两颗故障卫星识别的算法.

由式(6)可以看出，发生单星故障时，奇偶矢量p与故障特征向量Qp(:,i)成比例关系，也即两向量之间的夹角为0.若考虑观测噪声的影响，当已经检测到单星故障时，p与Qp各列向量之间的夹角最小的列向量所对应的卫星即可判断为故障卫星.同样的，由式(7)可以看出，p是两故障特征向量Qp(:,i)和Qp(:,j)的线性组合，即p位于Qp(:,i)和Qp(:,j)组成的故障特征平面上.若考虑观测噪声的影响，p与Qp(:,i)和Qp(:,j)组成的故障特征平面有一夹角.由Qp各列向量两两组合可以得到n(n-1)/2个这样的故障特征平面，求出与p夹角最小的故障特征平面，则可以判断构成此故障特征平面的故障特征向量所对应的卫星发生故障.通过这种几何算法，可以有效降低识别门限的影响，从而降低了漏检与误警的发生.

由第2节中分析可知，以上几何算法仍然存在故障偏差抵消的情况，为了解决这一问题，本文构造了与p相对应的另一奇偶矢量p′：

p′=qibi-qjbj

(10)

此时，有以下两种情况：

(1)bi·bj>0且qi(n)·qj(n)>0，或bi·bj<0且qi(n)·qj(n)<0时，p′(n)的值可能为0，

p(n) =qi(n)bi+qj(n)bj

=±(|qi(n)|·|bi|+|qj(n)|·|bj|)

(11)

(2)bi·bj>0且qi(n)·qj(n)<0，或bi·bj<0且qi(n)·qj(n)>0时，p(n)的值可能为0，

p′(n) =qi(n)bi-qj(n)bj

=±(|qi(n)|·|bi|+|qj(n)|·|bj|)

(12)

由式(11)、(12)可以知道，无论以上两种情况发生哪一种，总有p(n)、p′(n)中一个的值不可能为0，进而奇偶矢量p、p′总有一个不为0向量，故障偏差相互抵消的情况也由此得到解决.

由以上分析可知，通过奇偶矢量与故障特征平面之间的几何关系以及构造新的奇偶矢量可以极大提高双星故障识别的能力.为了方便阐述双星故障识别算法，以下用p统一代表p、p′.定义fi为第i颗卫星的归一化的特征向量，即

(13)

定义S为第i、j颗卫星的故障特征向量组成的故障特征平面，即

S=span(fi,fj)

(14)

(15)

(16)

其中

(17)

至此，可将双星故障检测与识别算法总结如下：

(1)对系数矩阵H进行QR分解，得到奇偶空间矩阵Qp；

(2)由式(5)得到奇偶矢量，p对y中的每一个元素分别取反，再应用式(5)得到n个对应的奇偶矢量p′.由给定的误警率指标得到双星故障检测门限TD，比较pTp、(p′)Tp′与TD的大小，若pTp、(p′)Tp′中任意一个的值大于TD，继续下一步，否则结束当前周期；

(3)由式(13)得到n个故障特征向量fi；

5 仿真及验证

为验证本文改进的双星故障识别算法，利用MATLAB对GPS卫星定位系统发生双星故障时算法的性能进行仿真，并与常规奇偶矢量双星故障识别算法、基于故障特征平面双星故障识别算法进行比较.本文所用数据来源于真实的卫星观测数据文件以及星历文件，观测文件数据始于2012年12月13日10点0分15秒，止于2012年12月13日10点41分15秒；给定σ=5m，误警率α=0.00001.

对单颗卫星加入时长为900s、幅值为4σ～10σ的故障偏差，单星故障识别率如图2所示.从图2可以看出，传统单星故障识别算法的识别率在故障幅值小于40m时，故障识别率低于80%；利用奇偶矢量与特征矢量的夹角最小规则来识别单星故障，即使故障幅值为20m时，故障识别率也高于80%，随着故障幅值的增加，故障识别率达到了90%以上.

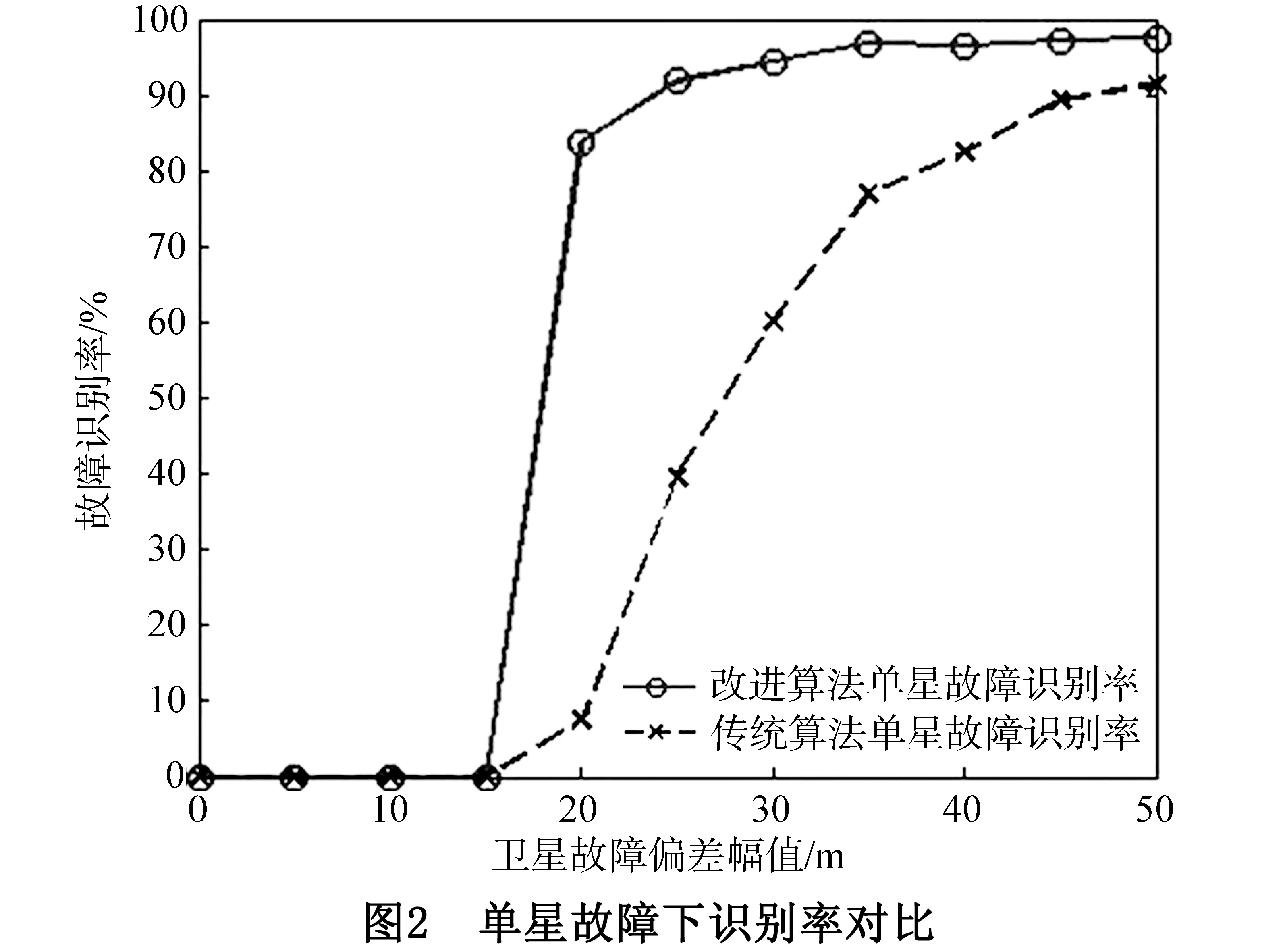
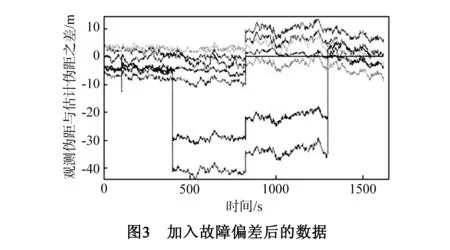
对15、18两颗星在2012年12月13日10点06分55秒时分别加入时长为900s、幅值为5σ和7σ的故障偏差，数据如图3所示.

仿真中对不同的两颗卫星组合分别加入幅值为-10σ～-4σ、4σ～10σ的故障偏差，得到的双星故障识别结果如图4所示.图4中，x、y轴分别表示两颗卫星上故障幅值与σ的比值.从图4(a)可以明显看出，当两颗卫星的故障偏差同号时，故障幅值的增加对故障识别率的影响很小，故障识别率很低，不足40%；故障偏差异号时，故障识别率超过了40%，当故障幅值为-7σ～-4σ、4σ～7σ时，故障识别率均在50%以下，随着故障幅值的增大，故障识别率有所提高，但仍低于80%.由图4(b)可以看出，相比于常规奇偶矢量双星故障识别算法，该算法可以明显提高双星故障识别率，但由于没有考虑故障偏差抵消的情况，当两颗卫星故障偏差同号且故障幅值较低时时，故障识别率在70%左右，随着故障幅值的增加，故障识别率提高到80%.由图4(c)可以看出，采用改进的故障识别算法以后，在两颗星故障偏差同号的情况下，故障识别率大于90%，特别地，当故障幅值在-10σ～-7σ、7σ～10σ时，故障识别率达到95%以上；在两颗星故障偏差异号时，故障识别率均大于90%甚至95%以上.

6 计算量比较

在可见星为8颗时，取100次正确识别故障时间的均值作为单次故障识别时间.3种算法计算量比较结果如表1所示.仿真所使用的计算机主频为3.0GHz.

从表1可以看出，由于本文提出的改进算法与常规算法和文献[10]算法相比，奇偶矢量个数或故障特征平面数有所增加，导致计算量有所增加，但故障识别性能却大大高于传统算法，在两颗卫星故障偏差同号识别率上也大于文献[10]算法.这里用计算量的增加换取了识别率的提高，而增加的计算量对故障识别的影响较小.因此本文提出的算法实用性较好.

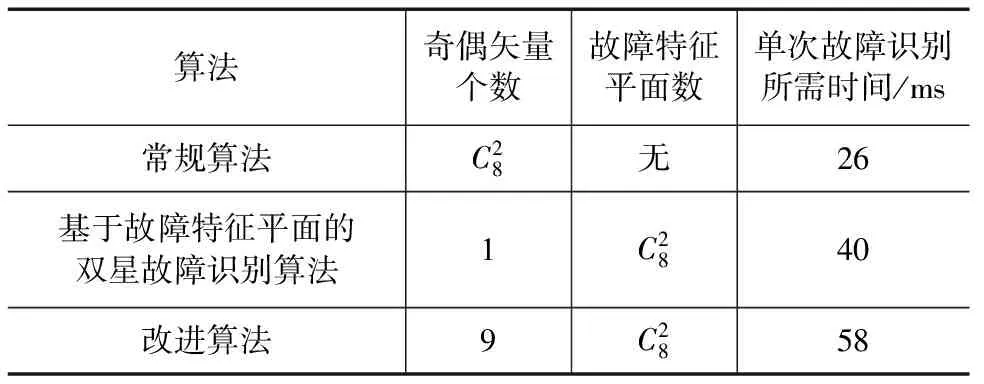
表1 各算法计算量比较

7 结论

理论分析和半物理仿真结果表明，利用传统双星故障识别算法进行故障识别时，由于其存在误警、漏检以及故障偏差抵消等不足，故障识别率不高，尤其在两颗卫星故障偏差同号时，故障识别率不足40%.采用基于故障特征平面的双星故障识别算法进行故障识别时，对两颗卫星故障偏差同号的识别率不足80%.本文在传统双星故障识别算法的基础上构造故障特征平面和改进奇偶矢量，通过二者之间的几何特征与卫星故障的关系来识别故障卫星，该方法可避免误警、漏检及故障偏差抵消造成的识别率较低的问题.仿真结果表明，当故障幅值在-10σ～-4σ、4σ～10σ时，改进的双星故障识别算法无论两颗星故障偏差是否同号，故障识别率都可以达到90%以上.这为双星故障识别算法提供了一种新的思路和方法.

[1]Lee Y C.Performance of receiver autonomous integrity monitoring (RAIM) in the presence of simultaneous multiple satellite faults[A].Proceedings of the 60th Annual Meeting of the Institute of Navigation[C].Dayton,Ohio,USA:ACM,2004.687-697.

[2]Liu J,Lu M,Cui X,et al.Theoretical analysis of RAIM in the occurrence of simultaneous two-satellite faults[J].Radar,Sonar & Navigation,IET,2007,1(2):92-97.

[3]Blanch J,Walker T,Enge P,et al.Baseline advanced RAIM user algorithm and possible improvements[J].Aerospace and Electronic Systems,2015,51(1):713-732.

[4]Tmazirte N A,Najjar M E E,Hage J A,et al.Fast multi fault detection & exclusion approach for GNSS integrity monitoring[A].2014 17th IEEE International Conference on Information Fusion (FUSION)[C].Salamanca,Spain:IEEE,2014.1-6.

[5]侯彦东,文成林,陈志国.多传感器故障检测与隔离的残差产生器设计方法研究[J].电子学报,2011,39(2):429-434. Hou Yan-dong,Wen Cheng-lin,Chen Zhi-guo.Designing method of residual generator for multi-sensor fault detection and isolation[J].Acta Electronica Sinica,2011,39(2):429-434.(in Chinese)

[6]孙国良,孙明茜,陈金平.时-集综合的接收机自主完好性监测方法研究[J].航空学报,2006,27(6):1171-1175. Sun Guo-liang,Sun Ming-xi,Chen Jin-ping.A study on time and set combined method for receiver integrity[J].Acta Aeronautica et Astronautica Sinica,2006,27(6):1171-1175.(in Chinese)

[7]张强,张晓林,常啸鸣.用于两颗故障卫星的RAIM算法[J].北京航空航天大学学报,2008,34(7):773-777. Zhang Qiang,Zhang Xiao-lin,Chang Xiao-ming.RAIM algorithm for identifying simultaneous two-faulty satellites[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(7):773-777.(in Chinese)

[8]Cao K,Hu Y,Xu J,et al.Research on improved RAIM algorithm based on parity vector method[A].2013 IEEE International Conference on Information Technology and Applications (ITA)[C].Chengdu,China:IEEE,2013.221-224.

[9]Salgueiro F,Sanguino J,Rodrigues A,et al.Weighted total least squares RAIM algorithm using carrier phase measurements[A].2012 6th IEEE ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing[C].Noordwijk,Holland:IEEE,2012.1-6.

[10]赵琳,李亮,程建华,等.用于识别双星故障的RAIM算法[J].北京航空航天大学学报,2010,36(11):1261-1265. Zhao Lin,Li Liang,Cheng Jian-hua,et al.New RAIM algorithm for identifying simultaneous double-faulty satellites[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(11):1261-1265.(in Chinese)

[11]刘海颖,王惠南,陈志明.卫星导航原理与应用[M].北京:国防工业出版社,2013.199-200.

[12]Wang E,Cai M,Pang T.A simple and effective GPS receiver autonomous integrity monitoring and fault isolation approach[A].Proceedings of the 2012 International Conference on Control Engineering and Communication Technology[C].Liaoning,China:IEEE Computer Society,2012.657-660.

[13]Pervan B S,Lawrence D G,Parkinson B W.Autonomous fault detection and removal using GPS carrier phase[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(3):897-906.

武永明 男,1990年出生于甘肃省天水市.现为北京航空航天大学仪器科学与光电工程学院硕士研究生.主要研究方向为组合导航和GNSS完好性监测技术.

E-mail:jiazoun@163.com

李 魁 男,1985年出生于陕西省西安市.2012年毕业于北京航空航天大学仪器科学与光电工程学院.现为北京航空航天大学电子信息工程学院博士后.主要研究方向为惯性/卫星/多源组合导航相关技术.

E-mail:eric.lee-buaa@buaa.edu.cn

Improved RAIM Algorithm for Identifying Simultaneous Two-faulty Satellites Based on Faulty Feature Plane

WU Yong-ming1，LI Kui1,2，LÜ Yan-hong1，WANG Ling-cao1

(1.CollegeofInstrumentationScienceandOpto-ElectronicsEngineering,BeihangUniversity,Beijing100191,China; 2.CollegeofElectronicandInformationEngineering,BeihangUniversity,Beijing100191,China)

Traditionally,the receiver autonomous integrity monitoring (RAIM) algorithm such as parity vector method for identifying two-faulty satellites based on identification threshold led to not only higher missed detection rate but also higher false alarm rate and fault counteraction,which decreased the correct identifying ratio.Therefore,an improved RAIM algorithm was proposed.On the basis of parity vector method,the improved algorithm constructed a faulty feature plane,and faulty satellites were identified by the geometry relationships between the plane and the proposed parity vector.These made the algorithm immune to the problem of high identifying threshold and improved the identifying ratio.Semi-physical simulation results indicated that the correct identifying ratio of the proposed algorithm reached 90%,and the performance was improved compared with the traditional algorithm.

receiver autonomous integrity monitoring (RAIM) algorithm;parity vector;faulty feature plane;fault identification

2015-04-27；

2015-08-31；责任编辑：覃怀银

国家自然科学基金(No.L142200032)；中国工程科技中长期发展战略研究基金(No.2014zcq01)

V474.2；TN967.1

A

0372-2112 (2016)12-2829-05

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.12.003