基于局部分布的k-最近邻分类方法
2017-01-10叶建龙
叶建龙
(陇南师范高等专科学校数信学院,甘肃成县 742500)
基于局部分布的k-最近邻分类方法
叶建龙
(陇南师范高等专科学校数信学院,甘肃成县 742500)
k-最近邻分类算法通过对待测样本的邻近样本进行分析来预测待测样本的类标号,是一种简单有效的分类方法.传统的k-最近邻算法通常使用邻近样本的多数投票规则来确定类标号.本文提出一种改进的k-最近邻算法,从邻域的局部分布来分析待测样本的类别.我们分析了局部分布特征对分类的影响,通过局部分布特征估计样本对每个类的隶属度,待测样本被分到最大的隶属度的类中.实验结果表明改进的方法能一定程度上提高分类准确率.
近邻分类;数据挖掘;算法
1 引言
分类问题是数据挖掘领域一个重要的研究方向,而近邻分类算法是研究分类问题的一个重要并广泛使用的方法.近邻分类算法的基本思想是根据待测样本在训练集中的近邻样本对该待测样本进行分类.k-最近邻算法(kNN)最初是由Cover和Hart[1]提出的,他们先从训练样本集中找到与待测样本最近的k个样本,称为待测样本的k个最近邻,然后将待测样本分到其k个最近邻所代表的多数类中.近几十年来,k-最近邻分类方法以其算法简单有效而广泛应用于模式识别和数据挖掘的各个领域[2,3,4],并被评为数据挖掘领域影响最大的十种算法之一[5].
如果一个数据集中同类的样本点近似度比不同类的样本点高,这个样本点的邻近样本就较远的样本比更能表现这个样本的性质,k最近邻算法在这种情况下就非常有效.实际上,被分为同类的样本通常会有某些相似性,因此,如果给定的特征足够,kNN算法通常能表现良好的分类效果.
传统的kNN算法是以待测样本的k个最近邻投票的形式确定类标号的,这种投票方法的缺点是没有考虑k个最近邻之间的差异,把这k个最近邻等同对待.虽然当邻域很小时,这种差异可以忽略不计,但是实际上由于数据集的不同,我们并不能保证所有样本的k个最近邻都在很小的区域内.因此,传统的kNN算法对某些样本的分类会出现误分情况.
文献中针对这个问题对kNN的改进方法主要有两类,第一类是通过对k个最近邻进行加权的方法来区分对待测样本分类的贡献,这种方法称为加权k最近邻方法(Weighted-kNN,WkNN)[6,7,8].第二类方法是将这k个近邻按类别规约为几个局部中心,根据中心到待测样本的距离来确定类标号,这类方法有类平均模式(Categorical Average Patterns,CAP)[9]和局部概率中心(Local Probabilistic Center,LPC)[10]等.
本文从局部分布的角度来研究分类问题并提出基于局部分布的k最近邻分类方法(Local Distribution based kNN,LD-kNN).一个样本的类标号与它周围样本的分布是密切相关的,我们可以根据待测样本的k个最近邻的分布特征计算出该样本对各个类的隶属度,然后将待测样本分到最高隶属度的类中.在UCI数据集上的实验结果表明该方法的有效性.
2 相关算法
给定一个样本X和它在训练集中的的k个最近邻,第i个最近邻记为(xi,Li),xi为特征描述,Li为类标号,其到X的距离记为di.K最近邻算法的任务就是组织这些信息对待测样本X进行分类.常用的方法有投票方法(V-kNN),距离加权方法(DW-kNN)和局部中心方法(LC-kNN).
2.1 V-kNN
V-kNN是最基础的k最近邻分类方法,它是从k个最近邻的投票来产生分类结果,V-kNN分类可以表示成如下公式

I(c)是指示函数,当条件c为真时返回1,否则返回0.Nc表示k个最近邻中类标号是C类的个数.
2.2 DW-kNN
DW-kNN是对传统V-kNN的一种改进,它通过对k个最近邻样本进行加权来区分不同近邻样本对分类的贡献,距离较近的样本更能反映待测样本的特征,因此DW-kNN会给较近的样本一个较大的权重进行投票.如果给第i个样本的权重是,DW-kNN可以表示为
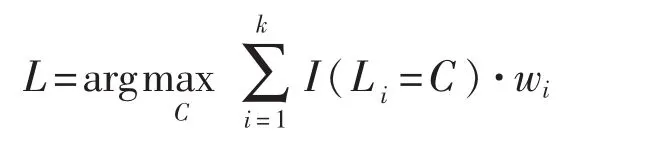
权重wi和该近邻到待测样本的距离di是密切相关,距离越大,该近邻对待测样本的影响越小,权重就越小.很多文献[6,7,8]都提出了不同的加权方法.最典型的就是Dudani[6]提出的加权方法,表示如下
2.3 LC-kNN
LC-kNN提取待测样本周围每个类的局部中心信息,然后将待测样本分到局部中心最近的类中.这种方法将待测样本的k个最近邻按类标号分组整体考虑,有效降低了k个最近邻中噪声点的影响.LC-kNN可以表示如下

其中d()表示两个样本点的距离.XC表示C类的局部中心.通常估计如下

由于每个类选取不同数据的近邻会对局部中心的估算造成偏差,CAP方法通过对每个类选择相等数量的最近邻来优化LC-kNN.假设对每个类都选k个最近邻,表示C类的第i个最近邻,CAP的局部中心就可以表示为

LPC方法对训练集的每个样本计算一个概率p表示它真正属于指定类的概率,即pi表示Xi属于Li的概率.通过这个概率来对训练集的噪声样本进行处理.这样,LPC的局部概率中心就表示为

3 本文的算法
我们通过每个类在待测样本周围的局部分布信息来估计待测样本对各个类的隶属度.本文用到的局部分布信息包括分布的中心和分布的离散程度两个指标.对单变量来说,变量的均值是其中心,标准差代表了其离散程度.对分类问题来说,一个样本通常是有多个变量表示,变量的分布就是多为分布.因此需要将均值和标准差扩展到多变量.n个样本X1,……Xn的中心和离散程度可以表示如下:
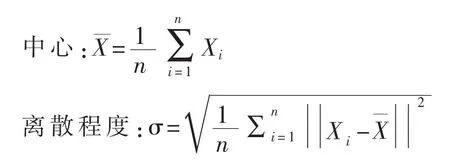
对于给定训练集T和待测样本q,LD-kNN的分类过程如下:
1.从训练集T中找出样本q的k个最近邻组成近邻集合Nk(q).即
Nk(q)={x|d(x;q)≤d(Xk;q);x∈T}
其中Xk表示第k个最近邻,d()为距离函数,表示两个样本之间的距离,本文选用欧氏距离.
2.根据类标号将k最近邻集合Nk(q)划分为Nc个小集合Si(i=1,……,Nc),使得每个集合中所有样本都属于同一个类,而不同集合中的样本属于不同的类.即

其中NC代表k个最近邻中类的总个数,Nj表示第j个类中包含在k个最近邻中的样本数.

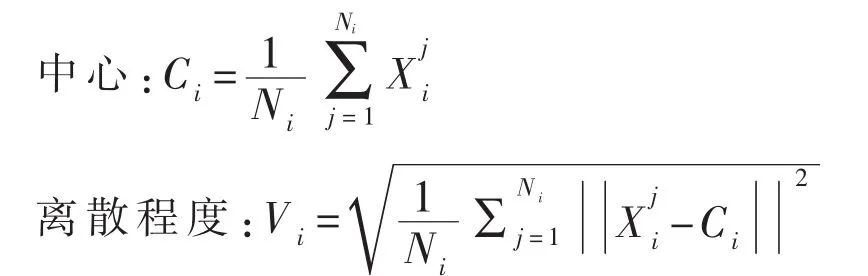
4.根据中心和离散程度来估计该样本对该类的隶属度MDi(q).直观来看,类的局部分布对隶属度的影响如下:1.类的离散程度相同的情况下,样本到类中心的距离越近,该样本对该类的隶属度越大.2.类的离散程度越大,即类越分散,它覆盖一个样本的可能性就越大,换句话说,一个样本到几个类中心距离相等时,该样本更可能属于离散程度较大的类.另外,3.由于Ni/k代表了待测样本q周围第i类分布的先验概率,Ni越大,q对第i类的隶属度就越大.因此,我们假设有如下关系:


表1 摇实验数据集

4 实验结果及分析
5.将待测样本q分到MDi(q)最大的类中,即
4.1 实验数据
本文用UCI的4个学习文算法进行了实验验证[11],选用的数据集信息如表1.
4.2 实验设置
对每个数据集我们进行如下实验设置:
1.交叉验证:我们使用5折交叉验证进行测试.对每个数据集均匀划分成5份,其中4份作为训练集,剩余一份作为测试集,分类精度为所有测试集中正确分类的样本数除以总的测试样本数.由于训练集和测试集是独立的,交叉验证能有效避免过拟合的问题.
2.规范化:对数据集的每个特征,我们使用z-score规范化将训练集中的特征转换为均值为0,标准差为1,测试集用相同的均值和标准差进行变化.变换公式如下:

3.评价指标:我们执行10次5折交叉验证,每次的划分是随机划分的,我们将10次5折交叉验证的平均分类精度作为评价指标.平均分类精度越高,分类效果越好.
4.参数选择:kNN分类器中的参数k表示搜索的近邻的个数.在我们的实验中,我们搜索近邻的个数为k*NC,NC为类的数目,即在待测样本周围平均每个类有k个近邻.我们将k从1到30变化,得出最高的分类精度作为该分类器在该数据集上的评价指标.
4.3 实验结果及分析
在实验数据集上不同kNN分类方法的比较结果如下表所示

表2 摇不同分类方法在不同数据集上的分类精度
从表2可以看出,在这四个数据集上,LD-kNN的分类精度都要高于其他方法,验证了LD-kNN的有效性.
参数k是一个能影响LD-kNN分类器分类效果的重要因素.如果k选择太小,对局部分布特征的估计会不很稳定,当k=1时,LD-kNN就变成了传统的最近邻分类方法.如果k的选择过大,那么有的近邻样本就会离待测样本较远,无法反映待测样本特性,反而对分类有负影响.因此,针对不同数据集要选择合适的参数k以提高分类精度.
5 结语
基于局部分布的思想,我们提出以一种新的k最近邻分类方法.这种方法将待测样本周围的样本按类别整体考虑,计算各类的局部分布特征,然后根据局部分布特征计算待测样本对于各个类的隶属度,样本被分到具有最大隶属度的类中.由于对局部近邻的整体考虑,该方法表现出比传统kNN方法更好的分类效果.
[1]T.Cover and P.Hart,“Nearest neighbor pattern classification,”Information Theory,IEEE Transactions on,vol.13, no.1,pp.21-27,1967.
[2]D.Hand,H.Mannila,and P.Smyth,Principles of data mining.MIT press,2001.
[3]Y.Zhou,Y.Li,and S.Xia,“An improved knn text classification algorithm based on clustering,”Journal of computers, vol.4,no.3,pp.230-237,2009.
[4]J.Bromley and E.Sackinger,“Neural-network and k-nearest-neighbor classifiers,”Rapport technique,pp.11 359-910 819,1991.
[5]X.Wu,V.Kumar,J.R.Quinlan,J.Ghosh,Q.Yang,H. Motoda,G.J.McLachlan,A.Ng,B.Liu,S.Y.Philip et al.,“Top 10 algorithms in data mining,”Knowledge and Information Systems,vol.14,no.1,pp.1-37,2008.
[6]S.Dudani,“The distance-weighted k-nearest-neighbor rule,”Systems,Man and Cybernetics,IEEE Transactions on, no.4,pp.325-327,1976.
[责任编辑:王晓军]
O 176.3
A
1672-402X(2016)11-0013-04
2016-08-10
叶建龙(1981-),男,甘肃西和人,陇南师范高等专科学校讲师,研究方向:数据挖掘、算法.
