一类广义Lorenz-Stenflo超混沌系统的局部稳定性及fold分岔研究

陈玉明

（广东技术师范学院计算机科学学院，广东广州 510665）

一类广义Lorenz-Stenflo超混沌系统的局部稳定性及fold分岔研究

陈玉明

（广东技术师范学院计算机科学学院，广东广州 510665）

针对一类广义的Lorenz-Stenflo四维超混沌系统，基于Routh-Hurwitz准则，分别研究了该系统的原点平衡点及非原点平衡点为双曲平衡点时的局部稳定性，并利用含参中心流形方法，对该系统在原点平衡点处的fold分岔进行了研究，从而获得了原点平衡点为非双曲时的稳定性行为.

Lorenz型系统；超混沌；稳定性；fold分岔

1 引言

在1963年，Lorenz在研究气象模型时提出了第一个混沌数理模型，即Lorenz系统.从那以后，来自于不同领域的数学家、物理学家及工程师们便对混沌的起源、混沌系统的特征与分岔行为、通向混沌的路径等各个方面，都展开了深入地研究.超混沌，作为另一种复杂动力学行为，它比混沌行为具有更强的复杂性以及更强的应用潜力.由于在自治常微分方程系统中要产生超混沌行为，必须要求系统维数至少为四维，因此，对四维超混沌系统的研究，尤其是对四维Lorenz型超混沌系统的研究，将显得尤为重要.

在对于混沌系统的研究中，系统局部稳定性及分岔行为的研究是非常重要的一部分.随着系统平衡点稳定性的改变，即发生分岔行为，系统的局部动力学行为也会随之改变，甚至会引发系统全局动力学行为的变化.在稳定性的研究方面，针对经典的Lorenz系统，文献［5］给出了Lorenz系统零平衡点Lyapunov意义下全局指数稳定、全局渐近稳定以及不稳定的简洁的代数充分条件，也给出了两个非零平衡点局部指数稳定、不稳定及线性化系统稳定而非渐近稳定的代数充分条件.在fold分岔的研究方面，文献［6］利用间接法对一典型的电压稳定模型进行计算并确定了系统负荷的fold分岔值，而文献［7］则首次利用了含参中心流形的方法对电力系统中与电压崩溃相关联的fold分岔进行了简化分析.针对三维统一Lorenz型系统及一类四维Lorenz型超混沌系统，文献［8，9］分别对它们原点平衡点处的fold分岔进行了仔细地研究.

在1996年，Stenflo沿着Lorenz模型的方向，提出了描述大气扰动的一个简单模型，其被称为Lorenz-Stenflo系统［10］.该系统考虑了地球的旋转，黏度效应及热扩散效应等因素，该系统的方程为

基于上述的Lorenz-Stenflo系统，通过将该系统的参数可选取范围进行推广，本文考虑了如下的广义Lorenz-Stenflo系统

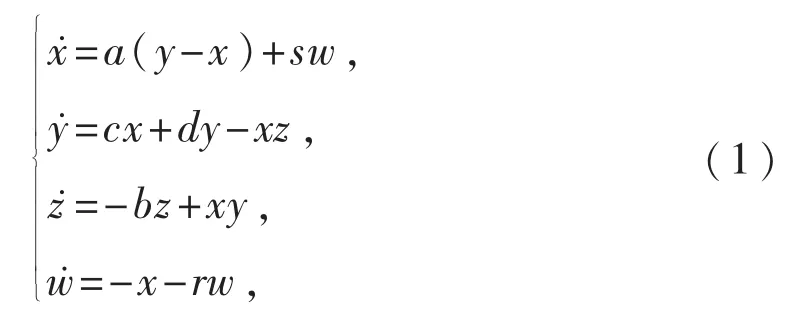
其中参数满足a>0，b>0，cdrs≠0.当系统参数选取a=19.42，b=1.91，c=29.45，d=-2.86，r= 0.23及s=9.64时，系统（1）具有超混沌吸引子，该吸引子所对应的Lyapunov指数为

λLE1=0.0696，λLE2=0.0359，

λLE3=0.0002，λLE4=-24.5176.

该超混沌吸引子在x-y-w空间的投影相图如图1所示.

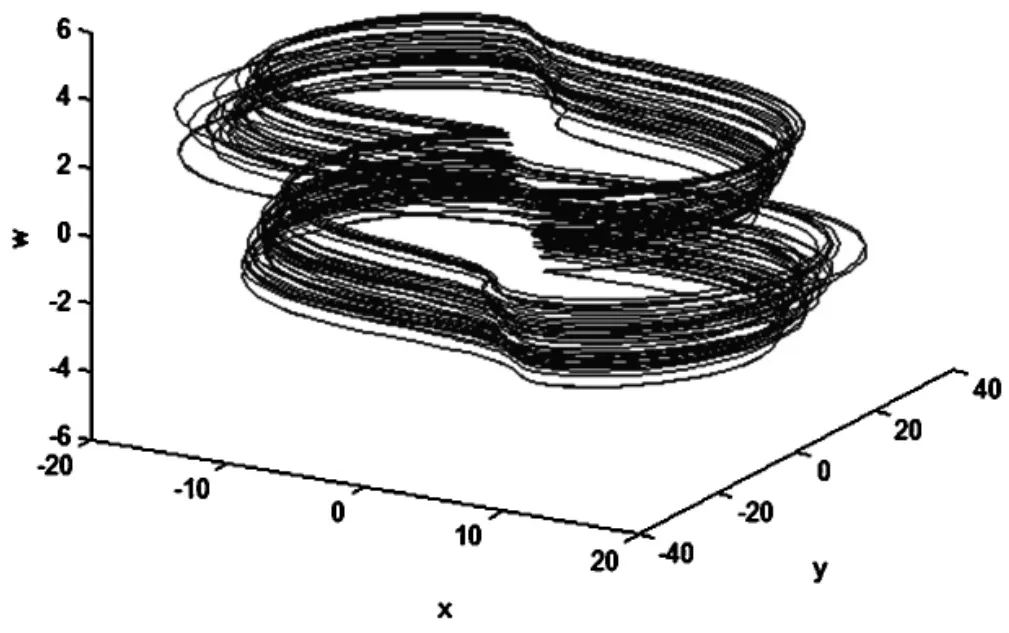
图1 系统（1）的超混沌吸引子在x-y-w空间的投影相图

当系统参数满足（ar+s）（ar（c+d）+ds）≤0时，系统（1）只具有唯一平衡点E0(0,0,0,0).而当（ar+ s）（ar（c+d）+ds）>0时，系统（1）除了具有原点平衡点E0之外，还将具有另外两个关于z轴对称的非原点平衡点

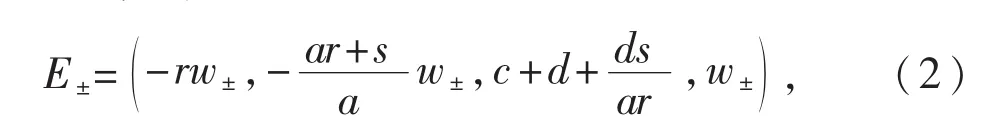
针对四维广义Lorenz-Stenflo超混沌系统（1），本文将研究该系统的原点平衡点E0及非原点平衡点E±为双曲平衡点时的稳定性，并且通过对原点平衡点E0的fold分岔研究，还将进一步得到原点平衡点E0为非双曲平衡点时的稳定性性质.

2 平衡点的局部稳定性

根据系统（1）的代数方程，可算得平衡点（x*，y*，z*，w*）处的Jacobian矩阵为

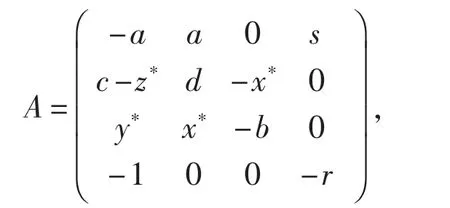
如下的两个定理分别研究了系统（1）的平衡点E0及E±为双曲平衡点时的稳定性性质.

定理1.当下述条件集合成立时，

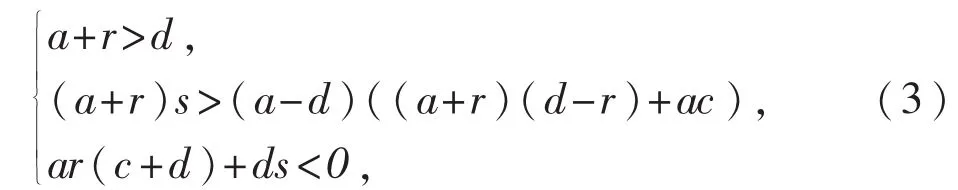
平衡点为双曲平衡点，并且是局部渐近稳定的.

证明.容易算得Jacobian矩阵A在平衡点E0处的特征方程为

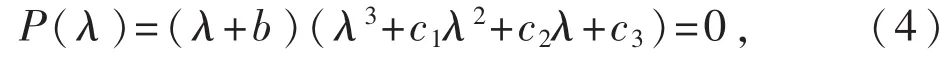
其中c1=a-d+r，c2=-ac-ad+ar-dr+s，c3=-acr-adr-ds.

计算如下的几个行列式：

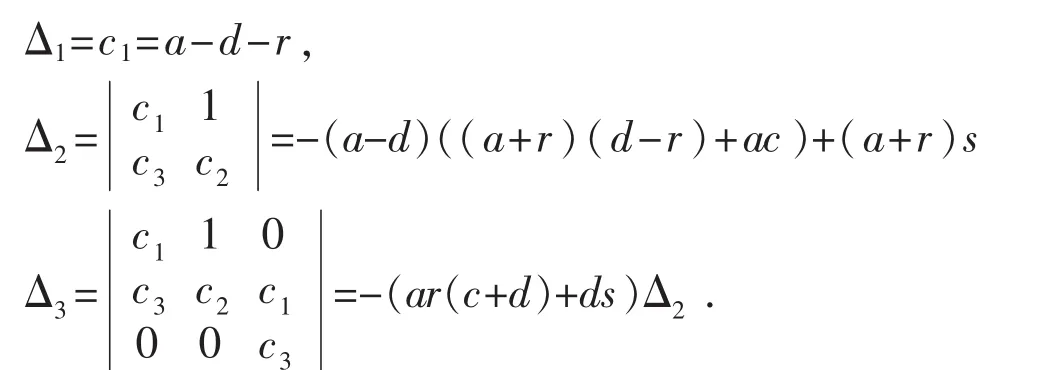
如果条件集合（3）成立，则可推得Δ1>0，Δ2>0及Δ3>0同时成立，而根据Routh-Hurwitz准则，可知特征方程（4）所有的根都将具有负实部，从而平衡点E0为双曲平衡点，并且为局部渐近稳定的.

由于系统（1）在坐标变换（x，y，z，w）→（-x，-y，z，-w）的作用下是保持不变的，于是平衡点E+及E-的稳定性性质将完全相同.因此，在下述定理中只需要研究平衡点E+的局部稳定性即可.

定理2.当参数满足（ar+s）（ar（c+d）+ds）>0时，且有如下的条件集合成立

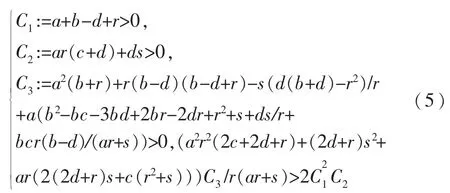
则系统（1）的非原点平衡点E+为双曲平衡点，并且是局部渐近稳定的.否则，平衡点为非双曲或不稳定的平衡点.

证明.如果参数条件（ar+s）（ar（c+d）+ds）>0成立，则系统（1）将具有一对对称的非原点平衡点E±，如表达式（2）所示.Jacobian矩阵A在平衡点E+处的特征多项式为

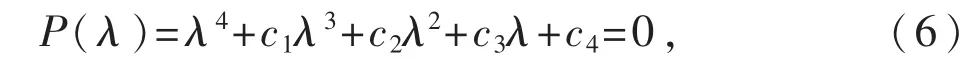
其中

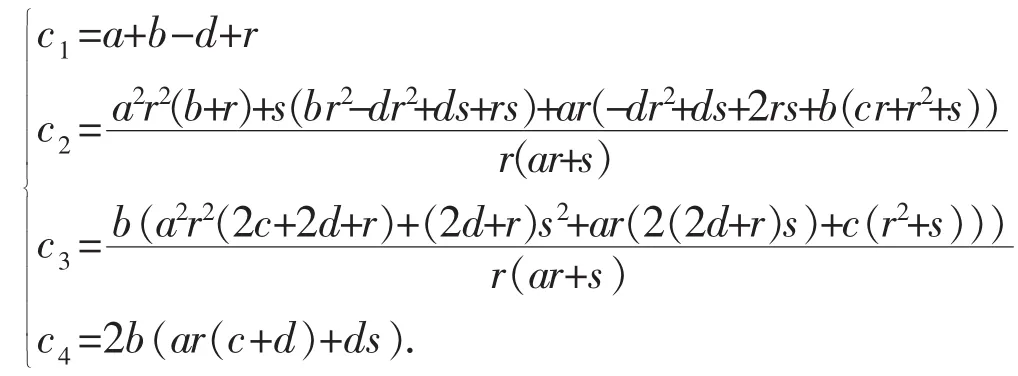
基于条件集合（5），可算得如下几个行列式

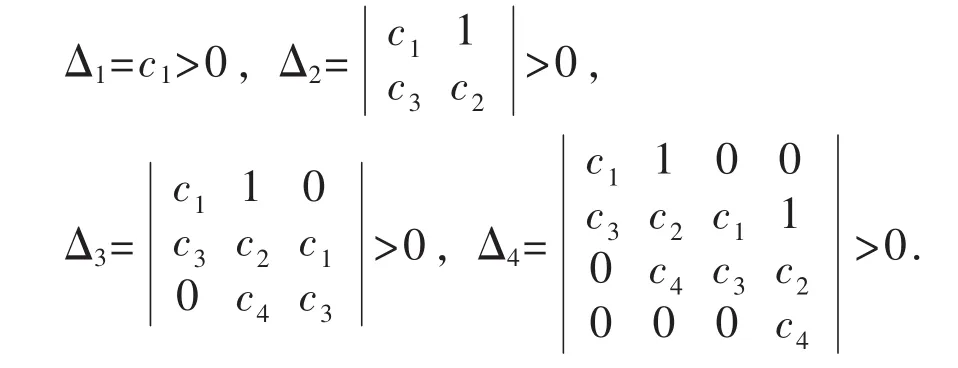
从而根据Routh-Hurwitz准则，可得特征多项式（6）的所有根都将具有负实部，于是系统（1）的非原点平衡点E+为双曲平衡点，并且是局部渐近稳定的.否则，如果条件集合（5）不成立，则特征多项式（6）的某些根将会具有非负实部，即零实部或正实部，从而使得平衡点E+为非双曲或不稳定的平衡点.

3 Fold分岔

通过使用含参中心留形理论以及规范形理论，本节将仔细地研究系统（1）在原点平衡点E0处的fold分岔，进而得到fold分岔临界状态下非双曲平衡点E0的稳定性性质，如下述定理所示.

定理3.令（a+r）d2+ac（d+r）≠0及d≠0，当参数s穿过临界值s0=-ar（c+d）/d时，系统（1）在平衡点E0处发生fold分岔，并且在fold分岔临界状态下，非双曲平衡点E0处的动力学性质如表1所示.

证明.由定理1的证明部分可知，系统（1）在平衡点E0处的特征方程如（4）所示.因此，当s=-ar（c+d）/d及（a+r）d2+ac（d+s）≠0时，特征方程（4）具有一个零根，以及三个具有非零实部的其它特征根.

为了确定在临界参数s=-ar（c+d）/d之下，非双曲平衡点E0的稳定性性质，考虑系统（1）的如下等价变换:

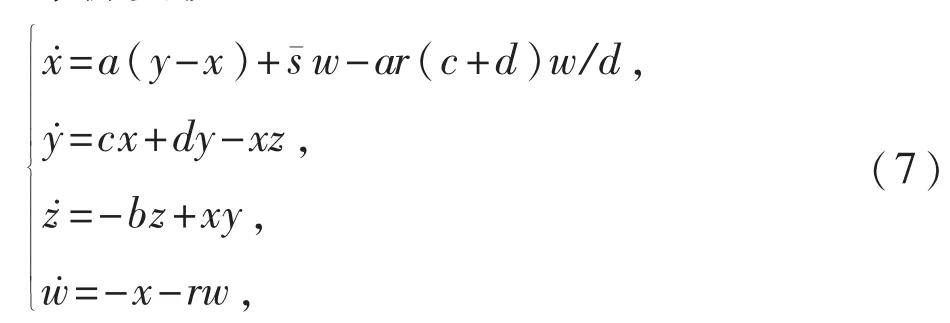
其中a，b，c，d及r被看成固定常数，而s¯= s+ar（c+d）/d则被当成变化参数.值得注意的是，在含参中心流形的讨论中，系统（7）中的项s¯w应该被看成是非线性项，并且原点E0也还是系统（7）的平衡点.在平衡点E0处将系统（7）进行线性化，可得对应的Jacobian矩阵为

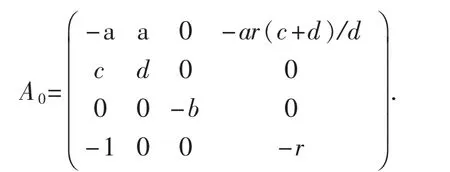
通过简单计算，可得矩阵A0的特征值为

在变换（x，y，z，w）T=（ξ3，ξ4，ξ1，ξ2）（u，v，p，q）T的作用下，系统（7）将变换成为如下形式的新系统：

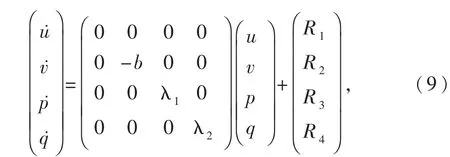
其中

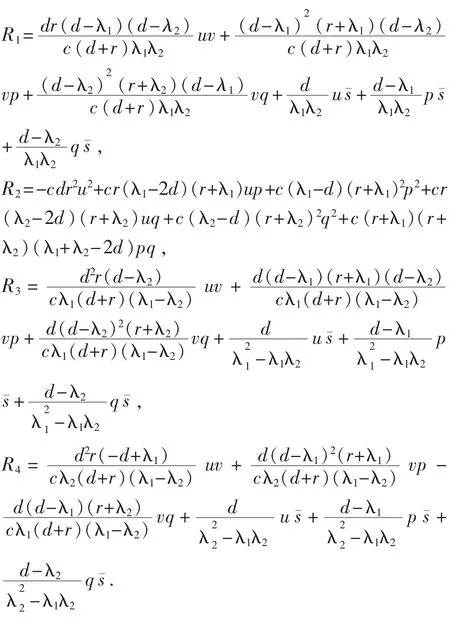
根据含参中心流形理论，平衡点E0在¯=0附近的稳定性可以通过研究一阶常微分方程在其中心流行上的双参数族来得到.这个中心流行可表示成为变量u及¯的一个图形，即

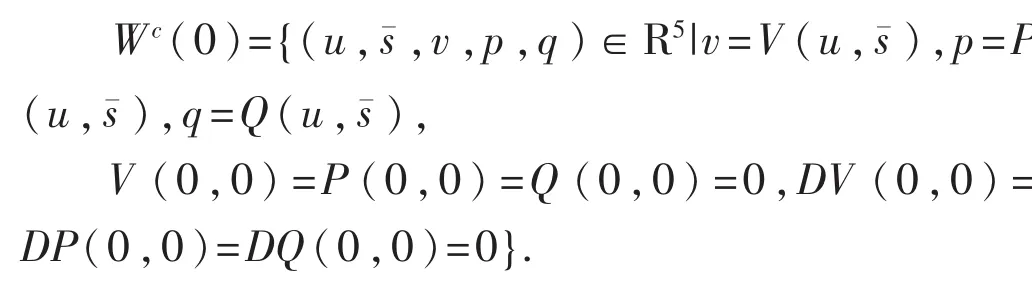
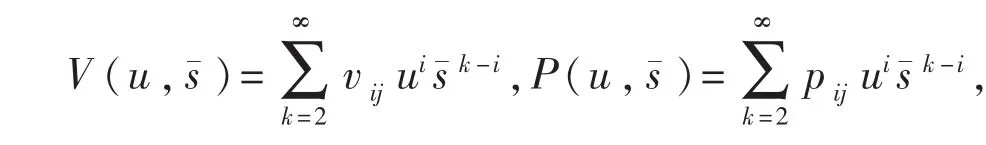
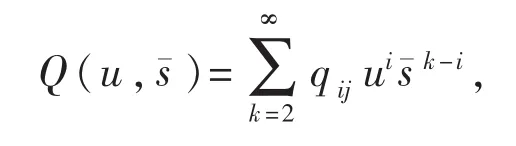
于是可计算得

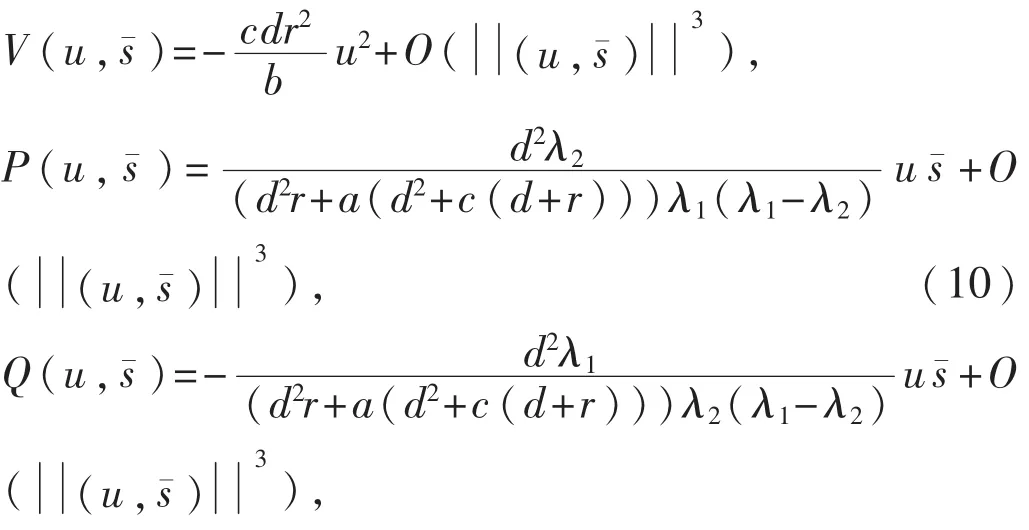
根据fold分岔的相关理论可知，当参数s穿过临界值s0=-ar（c+d）/d时，系统（1）在平衡点E0处发生叉形分岔.

考虑到系统（7）在平衡点E0处的特征值如（8）所示，由中心流形理论可知，系统（1）在非双曲平衡点E0处的如下动力学行为，见表1.

表1 摇系统（1）在fold分岔平衡点处的局部动力学行为

［1］E.N.Lorenz.Deterministic non-periodic flow［J］.J.Stmos. Sci.1963.20.130-141.

［2］M.W.Hirsh,S.Smale,R.L.Devaney.Differential Equations,Dynamical Systems,and an Introduction to Chaos［M］. New York:Elsevier Academic Press.2007.

［3］L.P.Shilnikov,A.L.Shilnikov,D.V.Turaev,et al.Methods of Qualitative Theory in Nonlinear Dynamics［M］.Singapore: World Scientific.2001.

［4］S.Wiggins.Introduction to Applied Nonlinear Dynamical Systems and Chaos.Second Edit［M］.NewYork: Springer-Verlag.1990.

［5］廖晓昕,罗琦.Lorenz混沌系统Lyapunov稳定性简洁的代数充要条件及其应用［J］.中国科学:信息科学,2010,40(8):1086-1095.

［6］曹国云,陈陈.间接法计算非线性电压稳定模型的平衡点分岔值［J］.电力系统自动化,1999,23(21): 17-20.

［7］曹国云,王冲,陈陈.中心流形方法降维分析电压崩溃中的Fold分岔［J］.中国电机工程学报,2002, 22(7):40-43.

［8］Q.Yang,Y.Chen.Complex dynamics in the unified Lorenz-typesystems［J］.Int.J.Bifurcat.Chaos. 2014.24.1450055(30 pages).

［9］Y.Chen,Q.Yang.Dynamics of a hyperchaotic Lorenz-type system［J］,Nonlinear Dynam.2014.77.569-581.

［10］Stenflo L.Generalized Lorenz equations for acousticgravity waves in the atmosphere［J］.Phys.Scr.1996;53: 83-84.

［责任编辑：刘向红］

Local Stability and Fold Bifurcation of a Generalized Lorenz-Stenflo Hyperchaotic System

CHEN Yuming

(School of Computer Science,Guangdong Polytechnic Normal University,Guangzhou 510665,China)

This paper approaches a generalized Lorenz-Stenflo hyperchaotic system.Basing on the Routh-Hurwitz principle,the stabilities of hyperbolic origin equilibrium and hyperbolic non-origin equilibria are investigated.Furthermore,with the help of the parameter-dependent center manifold theory,the fold bifurcation of this hyperchaotic system at origin equilibrium is investigated.Thus,the stability of the non-hyperbolic origin equilibrium is obtained.

Lorenz-type system;Hyperchaos;Stability;Fold bifurcation.

O 415

A

1672-402X（2016）11-0001-05

2016-04-22

广东省自然科学基金（主持人：陈玉明，No.2015A030310424）

陈玉明（1987-），男，江西赣州人，博士，广东技术师范学院讲师.研究方向：微分方程及动力系统.