大跨斜拉桥桩基础模拟方法分析

陈香杰， 曹 旭

(长安大学 公路学院， 陕西 西安 710064)

大跨斜拉桥桩基础模拟方法分析

陈香杰， 曹 旭

(长安大学 公路学院， 陕西 西安 710064)

以广州某中央双索面混凝土斜拉桥为工程背景，运用Midas Civil软件建立有限元模型，分析主塔桩基础模拟的3种方法：直接固结法、六弹簧模拟法和m法对主梁沉降、临时限位挡块受力和主塔沉降的影响。通过分析对比，得出结论：直接固结法模型计算的结构整体刚度偏大且对结构位移估计不足，计算出的主梁沉降较小，且临时限位挡块受力过大，主塔沉降不符合实际；六弹簧模拟法能够较合理地模拟塔底的约束情况，主梁沉降和临时挡块受力较合理，主塔沉降符合实际；m法模型能较详细地考虑桩基与桥梁结构的共同作用，并且能够反映桩土的共同作用，计算结果与六弹簧模拟法相近。因此，对于常规设计和计算，建议采用六弹簧模拟法。

斜拉桥； 桩基础； 直接固结法； 六弹簧模拟法； m法

0 引言

斜拉桥作为一个高次超静定的柔性结构，控制参数对其影响比较大。许多学者做了很多考虑桩土作用对大跨径斜拉桥特性影响的研究。文献[1，2]分析了考虑桩-土-结构相互作用对大跨度斜拉桥随机地震动响应的影响，指出建立在柔性地基上的大跨度斜拉桥应当合理考虑基础刚度效应和桩-土-结构动力相互作用，不能简单地把基础直接考虑为固结模式；文献[3，4]分析了考虑桩-土-结构相互作用对斜拉桥动力特性的影响，指出考虑桩土效应使得结构刚度降低，自震周期变长，对于大跨度斜拉桥的动力分析，需要考虑基础的桩土效应；文献[5]分析了考虑桩土水耦合效应下对斜拉桥非线性的影响，指出大跨度斜拉桥需要考虑几何非线性和材料非线性的作用。目前国内对考虑桩土效应对斜拉桥主梁沉降、临时限位挡块受力和主塔沉降影响的研究并不多见。本文旨在就主塔是否考虑桩土效应，建立3种斜拉桥桩基础模拟模型，分析其对大跨径斜拉桥主梁沉降、临时限位挡块受力和主塔沉降的影响。

1 桩基础分析方法

目前对桥梁桩基础常用的简化分析方法有直接固结法、等效嵌固法、弹性嵌固法、六弹簧模拟法和Winkler地基梁模拟法[6]等。本文只分析直接固结法、六弹簧模拟法和Winkler地基梁模拟法3种分析方法。分别建立有限元模型，命名为模型1、模型2和模型3。

1.1 直接固结法

直接固结法忽略了桩基的影响，采用简化的方法在主塔底部直接固结。这对于模拟一些小跨径桥梁是可行的。

1.2 六弹簧模拟法

六弹簧模拟法是在桥墩底部承台施加6个方向的弹簧来模拟群桩的作用，也就是在模型中输入6个方向的刚度来简化模拟群桩。这6个弹簧刚度分别是竖向刚度、顺桥向刚度、横桥向刚度的抗推刚度、绕竖轴的抗扭刚度和绕两个水平轴的抗弯刚度。各弹簧刚度是基于弹性地基梁法计算出沿桩长分布的土弹簧，并根据静力刚度等效原理，将其集中等效为承台底部的土弹簧刚度。

1.3 Winkler地基梁模拟法(m法)

Winkler地基梁模拟法将桩看成处于土体中的梁，将桩周围的土体对桩的动力阻抗用一系列连续分布又相互独立的弹簧以及阻尼器来代替，常用的分析方法有m法。m法指将桥梁结构与群桩基础共同考虑，将周围土体对群桩的作用模拟为沿桩深度变化的土弹簧，弹簧刚度根据《公路桥涵地基与基础设计规范》JTG D63 — 2007附录P计算。

3种模拟方法对比见表1。

表1 3种模拟方法对比桩基础模拟方法优点缺点使用条件直接固结法建模简单，运行速度快无法考虑桩土效应，分析结果与实际不符小跨径桥梁六弹簧模拟法建模简单，计算量小，与实际较相符无法考虑桩基础质量的惯性作用，对于高桩承台，忽略了桩的自由段大跨径桥梁、需进行动力分析的桥梁m法能准确反映桩土相互作用建模复杂，不能模拟弹塑性状态，水平荷载较大时，计算误差较大大跨径桥梁、需进行动力分析的桥梁

2 有限元模型

2.1 工程背景

某半漂浮体系双塔中央索面预应力混凝土斜拉桥，采用柱式索塔，斜拉索采用准辐射型布置，跨径布置为(60+150+380+150+60)m=800 m。主梁采用大悬臂单箱五室预应力混凝土箱梁。箱梁顶面宽40.8 m，底面宽21.6 m，梁高4 m，横隔板厚0.4 m。塔柱两侧分别设29对斜拉索，主梁索距6 m。整体布置如图1所示。

索塔基础采用20根直径3.0 m的钻孔灌注桩，横桥向桩间净距3.8 m，顺桥向桩间净距3.3 m。主梁采用复合式牵索挂篮悬臂浇筑施工，主梁通过主梁与索塔间的临时限位挡块和临时钢管桩临时固结。待施工至29#块时(主梁共分为29个块段，辅助墩顶处为23#块)，将主梁23#块横隔板加厚至2.4 m，并浇筑中央护栏间宽8 m，厚0.35 m，长度为56 m的压重混凝土，使主梁落在辅助墩顶支座处。待中跨合龙后拆除临时限位挡块和临时钢管桩，施工桥面铺装，完成施工。

图1 整体布置图(单位： cm)

2.2 模型建立

2.2.1 直接固结法(模型1)

将主塔、辅助墩和过渡墩墩底节点直接固结，模型见图2。

2.2.2 六弹簧模拟法(模型2)

主塔、辅助墩和过渡墩墩底节点采用一般弹性支撑模拟，在刚度矩阵中分别输入6个方向的刚度，如表2所示，模型见图3。

2.2.3 m法(模型3)

建立主塔群桩基础，主塔和群桩基础均采用梁单元模拟，由于桩顶处附近土体对桩基础的力学行为影响较大，土体弹簧的设置应采用“上密下疏”的原则，群桩基础距桩顶10 m内每2 m划分一个单元，10 m以下每4 m划分一个单元。本模型每

根桩基础共划分为16个节点和15个梁单元，如图4所示。各层土弹簧刚度如表3所示。

图2 直接固结法模型

表2 六弹簧模型中的弹簧刚度位置SDx/(kN·m-1)SDy/(kN·m-1)SDz/(kN·m-1)SRx/(kN·m·rad-1)SRy/(kN·m·rad-1)SRz/(kN·m·rad-1)主塔611×106628×106695×107389×109687×109100×1012辅助墩、过渡墩115×106115×106800×106957×107957×107100×1012

图3 六弹簧模拟法模型

图4 m法模型

表3 各层土弹簧刚度距桩顶位置/m弹簧刚度/(kN·m-1)距桩顶位置/m弹簧刚度/(kN·m-1)2138×1054399×1056701×1058985×10510129×10614460×10618938×10622108×10726129×10730159×10734455×10738850×10742934×10746996×10750243×108

3 结果分析

3.1 3种模拟方法对主梁线型的影响

因边跨合龙过程采用混凝土压重工艺，使梁落到辅助墩顶处与支座接触，完成合龙，因此该桥的立模标高应精确考虑。立模标高过大，造成后期边跨主梁支座脱空现象，影响桥梁的正常使用；立模标高过小，将会影响支座的安装，悬臂施工时主梁无法通过辅助墩。该桥主梁立模标高取值为：梁底设计标高+10 a收缩徐变+1/2汽车活载+累积位移。主梁的沉降和立模标高关系紧密，只有准确地模拟塔底桩基础的效应，确定立模标高，才能使施工更加安全、顺利。

由表4、图5可知，模型1的累积沉降值最小，由此得出的主梁立模标高也最小；模型2和模型3累积沉降值基本一致；在边跨23#块处模型1和模型2的累积沉降值相差14.9 mm，模型1和模型3相差15.3 mm，块段编号越大，两者的值相差越大。

表4 各模型主梁10a累积沉降值m位置模型1模型2模型3B290．37580．39260．3929B230．36530．38020．3806B170．28250．29450．2953B110．19410．20310．2043B060．12550．13230．1337B010．03460．03950．0409 注：限于篇幅，本文只提取边跨关键节点的沉降值，B29表示边跨29#块。

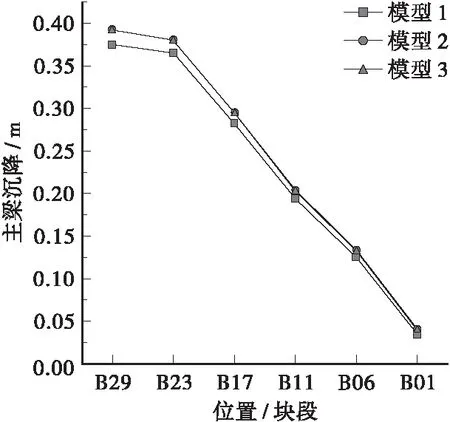
图5 主梁各节段沉降

3.2 3种模拟方法对临时限位挡块受力的影响

随着悬臂施工的进行，主梁和主塔之间的临时限位挡块受力越来越大，本文考虑中跨合龙预应力钢束张拉前、后和整体升、降温10 ℃时，临时限位挡块的受力情况，如表5、图6所示。

表5 各工况临时限位挡块受力情况kN模型中跨合龙束张拉前中跨合龙束张拉后整体升温10℃整体降温10℃模型1267×103246×104-532×104595×104模型2246×103129×104-261×104295×104模型3253×103117×104-259×104275×104 注：受力方向往中跨侧为正，往边跨侧为负。

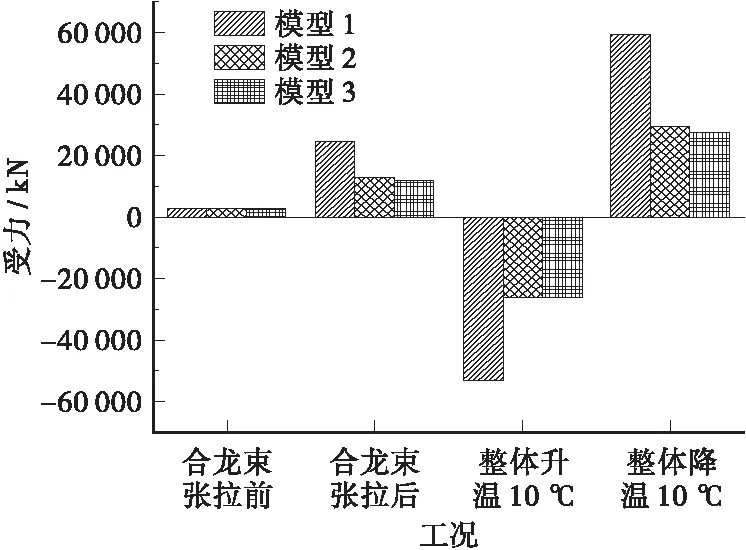
图6 各工况临时限位挡块受力

由表5可知，模型1各工况下临时限位挡块受力最大，特别是在整体升、降温10 ℃工况下，模型1和模型2分别相差2.71×104kN和3.00×104kN，相差率为103.9%和112.1%，模型1和模型3分别相差2.73×104kN和3.20×104kN，相差率为105.5%和115.9%。

3.3 3种模拟方法对主塔沉降的影响

将主塔顶部(高程117.762 m)定义成A截面，主塔与主梁相接处(高程33.147 m)定义成B截面，主塔底部(高程6.574 m)定义成C截面，将承台底部(高程-2.426 m)定义成D截面，计算各截面在成桥10 a后的沉降值。对比分析3种塔底模拟方式对主塔沉降的影响，结果如表6、图7所示。

由表6可知，塔底按固结模拟，主塔各截面10 a沉降值最小，D截面的沉降值为0，这与实际不相符；塔底按六弹簧模拟和按m法模拟，主塔10 a沉降值基本一致，最大相差2 mm，按六弹簧模拟和按m法模拟能够得到相似的结果；塔顶A截面处模型1和模型2最大相差6 mm，模型1和模型3相差8 mm；由表7、图8可知，塔底桩基础按m法模拟时，桩基距离桩顶位置越远，沉降值越小，当距离桩顶30 m时，沉降值仅为0.37 mm，距离超过30 m时，沉降值可忽略不计。

表6 主塔各截面10a沉降值m模型A截面B截面C截面D截面模型1-0055-0013-00010000模型2-0061-0019-0007-0006模型3-0063-0021-0008-0007

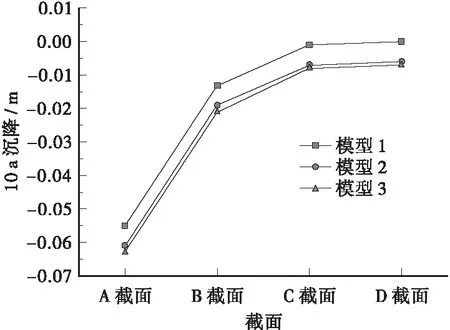
图7 主塔各截面沉降

表7 桩基各位置10a沉降值m距桩顶位置10a沉降距桩顶位置10a沉降2-745×10-34-665×10-36-581×10-38-500×10-310-424×10-314-324×10-318-227×10-322-131×10-326-710×10-430-370×10-434-180×10-438-600×10-542-200×10-546-100×10-550000

图8 桩基各位置沉降

4 结论

以某斜拉桥为工程背景，分析比较了几种常用的桩基础模拟方法，得到以下几个结论：

1) 对于无边跨压重和辅助墩的斜拉桥，塔底按3种方法模拟都能得到较准确的预拱度值；但是对于有边跨压重和辅助墩的大跨径斜拉桥，必须考虑塔底桩基础的桩土作用，塔底按固结模拟将产生较大偏差，在实际应用中应引起重视。

2) 塔底按固结模拟，使得结构的计算刚度较实际刚度大，在计算塔梁临时限位挡块受力时出现偏大现象；按六弹簧模拟法和m法得到的临时限位挡块受力较符合实际。

3) 按m法模拟桩基，当桩基埋深超过一定深度后，其沉降值非常小。建议当桩基埋深超过30 m后，可不必按实际桩长模拟桩基，以节约建模和计算时间。

4) 塔底固结法对结构实际的位移估计不足，实际桥梁不建议采取此简化方法模拟；m法能够更加真实地模拟桩土的相互作用，但建模工作量大，且须按规范计算出各层土体的土弹簧刚度，增加了计算工作量；六弹簧模拟法建模工作量小，且可得出与m法相似的结果，适于常规设计使用。

[1] 武芳文，薛成凤.桩 — 土 — 结构相互作用对超大跨度斜拉桥随机地震动响应影响研究[J].四川建筑科学研究，2010(2)：177-180.

[2] 段浪，金波.桩 — 土 — 结构相互作用对大跨度斜拉桥地震响应的影响[J].力学季刊，2011(1)：81-90.

[3] 陈永健，张超，许莉，等.考虑桩土效应的大跨度斜拉桥动力特性分析[A].第21届全国结构工程学术会议论文集第Ⅱ册[C]，2012.

[4] 雷坚，祝兵.考虑桩 — 土 — 结构相互作用的斜拉桥动力特性分析[J].广东公路交通，2008(4)：29-37.

[5] 陈文元.考虑桩土水耦合的大跨斜拉桥地震响应与可靠度研究[D].成都：西南交通大学，2006.

[6] 孔德森.桩土相互作用分析中的动力Winkler模型研究评述[J].世界地震工程，2005(1)：12-17.

1008-844X(2016)04-0071-05

U 448.27

A