快速成型技术中适应性分层方法

范孝良, 王进峰, 李传帅

(华北电力大学 能源动力与机械工程学院, 河北 保定 071003)

快速成型技术中适应性分层方法

范孝良, 王进峰, 李传帅

(华北电力大学 能源动力与机械工程学院, 河北 保定 071003)

熔融沉积制造工艺中, 三维模型的分层处理是造成台阶效应的直接原因.台阶效应会降低零件的表面质量.减小台阶误差的传统方法是减小分层厚度和选择合理的分层方向.为了解决传统方法中成型精度与成型效率难以协调的问题, 介绍了一种适应性分层方法, 首先求出能够反映模型表面形状的参考曲线, 然后根据参考曲线上曲率变化情况确定分层厚度.该方法适用于截面轮廓线为抛物线形状的零件, 在保证成型精度的前提下极大地缩短了成型时间, 同时建立成型时间的评价模型, 分析了成型时间的影响因素.

快速成型; 台阶效应; 适应性分层; 参考曲线

3D打印(3D printing)是一种快速成型技术, 按照ASTM F42标准的定义[1], 3D打印是采用打印头、喷嘴或其他打印机技术, 通过材料沉积来制造物体的技术.熔融沉积制造(FDM)工艺作为3D打印技术的一种, 将丝状热熔性材料熔化后从喷头内挤压而出, 并逐层沉积、固化成形[2].FDM工艺具有成型材料广泛、成本低、体积小等优点, 但也存在成型精度不高的问题.

三维模型的分层处理是快速成型技术中的一个关键环节[3], 快速成型技术中分层制造流程如图1所示.从数学原理上看, 分层切片是将三维几何模型分解为一定厚度的二维几何数据, 再将二维数据按层厚叠加成形.简单地说, 切片处理是一个分解与叠加的过程, 是用截面轮廓线对几何模型的近似表达[4 - 5], 从而产生一种不可避免的原理性误差, 即台阶效应[6]( staircase effect).

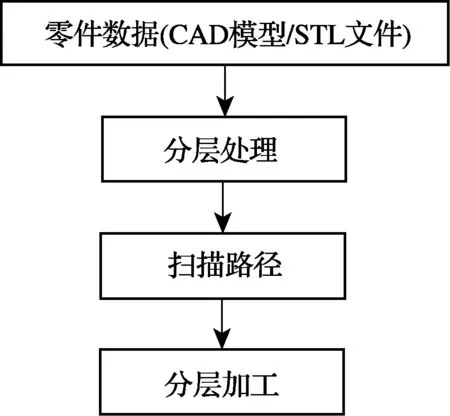
图1 快速成型分层制造流程Fig.1 Flow chart of rapid prototyping manufacturing

通过分层厚度的合理设定、分层方向的合理选择, 只能在一定程度上减小台阶效应对表面质量的影响.等层厚分层算法简单, 但台阶效应明显.兼顾制造精度和制造成本的适应性分层算法是目前研究的热点, 其原理是根据零件不同的轮廓特征而采用不同的分层厚度.分层厚度的确定是适应性分层算法的关键, 准确而快速地确定分层厚度是适应性分层算法中亟待解决的问题.为提高快速成型数据处理的精度和速度, 本文针对特定的轮廓特征, 提出了一种改进的适应性分层方法.

1 台阶效应

1.1 台阶效应的产生及影响

快速成型是一种分层制造技术[7], 当模型表面与零件的制作方向有一定角度时就会出现台阶效应, 如图2所示.台阶误差的评价指标为尖角高度δ, 表示沿模型表面法向量的方向, 曲边三角形的顶点到CAD模型表面的距离[8], 如图3所示.

(a) 三维CAD模型 (b) 层形件仿真模型图2 台阶效应Fig.2 Staircase effect

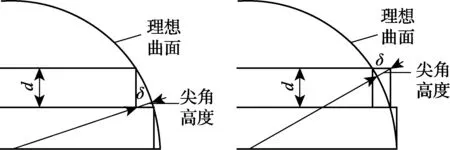
图3 分层制造的尖角高度Fig.3 Cusp height in layered manufacturing

台阶效应对成型精度的影响体现在下述3个方面.

(1) 台阶效应增加表面的粗糙度, 这表现为表面的阶梯状纹理.图4所示为设计的鼠标模型的成型件, 当层厚为0.2 mm时产生了明显的台阶效应.

图4 鼠标模型Fig.4 Computer mouse model

(2) 台阶效应会引起成型件的体积与三维CAD模型的体积误差, 表现为有些零件的体积减小, 而有些零件的体积增大, 如图5所示.

(a) 体积减小 (b) 体积增加图5 台阶效应造成的体积改变Fig.5 Volume change caused by staircase effect

(3) 台阶效应也会带来表面尺寸误差, 导致零件形状的畸变.当零件表面的局部特征尺寸小于分层厚度时, 该零件表面特征可能无法成形, 如图6所示.

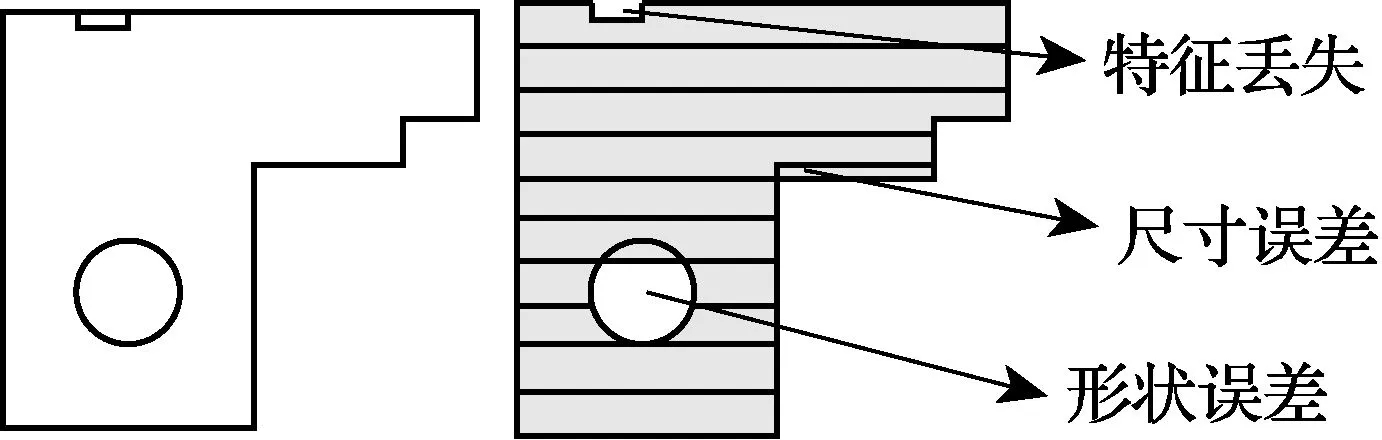
图6 台阶效应引起的零件特征改变Fig.6 Characteristics change of part from staircase effect

1.2 减小台阶效应的方法

台阶误差只与分层厚度、法线方向和模型的曲率有关[9], 如要减小这种误差, 传统的方法是减小分层厚度, 以及选择合理的分层方向[10].

(1) 合理的分层厚度.目前, 大部分快速成型系统采用等层厚分层方法.鼠标模型的分层效果如图7所示.由图7可知, 采用0.3 mm的层厚则台阶效应明显, 而采用0.1 mm的层厚则台阶效应减小, 但后者成型时间是前者的3倍.

(a) 层厚0.3 mm, 成型时间41 min

(b) 层厚0.1 mm, 成型时间120 min图7 鼠标模型分层效果图Fig.7 Delamination effect of the computer mouse model

(2) 合理的分层方向.在快速成型技术中, 与分层方向平行或垂直的零件表面不会出现台阶效应[11], 所以, 成形时应合理地选择分层方向.如图8中所示的哨子模型应按右图中位置摆放, 而左图中主要圆柱表面台阶效应明显, 圆柱直径尺寸误差和形状误差较大.显然此种方法无法照顾到复杂零件的各个表面.

图8 不同摆放位置时零件的台阶效应Fig.8 Staircase effect of part in different positions

2 改进的适应性分层方法

适应性分层方法是根据零件不同的表面轮廓特征而采用不同的分层厚度, 也称为自适应分层方法.在零件轮廓截面变化较小时采用较大的分层厚度, 在零件轮廓截面变化较大时采用较小的分层厚度.适应性分层方法的特点在于对零件成型成本和成型精度的权衡与协调.通过适应性分层可以明显地减小台阶效应, 提高零件的成型精度, 降低制造成本[12].

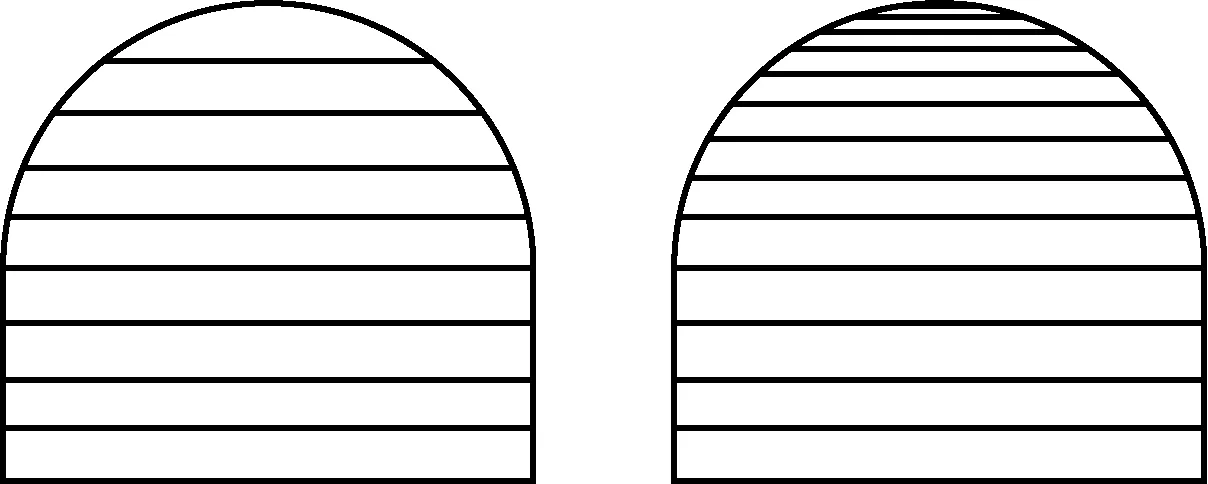
(a) 定层厚切片 (b) 适应性切片图9 适应性分层示意图Fig.9 The schematic diagram of adaptive slicing

2.1 适应性分层的原理和研究现状

分层厚度的确定是适应性分层的关键[13].层厚确定以后, 其他数据处理方法与等层厚切片时基本相同.在适应性分层切片时, 需要确定一种法则来判别分层厚度是否满足要求.根据判别法则的不同, 适应性分层方法主要分为法向量法、面积比较法和曲率法等.

Dolenc等[14]最早进行了基于STL(standard template library)模型的适应性分层方法的研究, 提出了尖角高度的概念, 具有启发性的意义.分层厚度根据上一层轮廓上各个点的法向量求出, 使尖角高度小于指定的表面误差， 如式(1)所示.

(1)

式中:d为分层厚度;Cmax为指定的表面误差;nz为模型法向量沿z轴的分量.

文献[15]提出了“面积比较法”, 通过计算相邻两层面积的变化率来确定分层厚度.根据判别公式, 判断层厚是否符合条件, 直至确定最终的分层厚度.但是该方法对于上下层面积相同的情况是不适应的.面积变化率的判别式为

(2)

式中:S1为上层切片截面面积;S2为当层切片截面面积;c为允许的面积变化系数,c可定义为5%[16].

文献[17]通过计算模型表面曲率的方法来优化分层厚度.层厚应满足规定的零件表面误差, 表面误差的大小用尖角高度δ表示.根据分层轮廓处采样点处的曲率, 用球面拟合零件表面的曲面, 从而计算分层厚度.采样点处的曲面拟合分为图10所示的4种情况, 分层厚度的计算式分别为

(3)

(4)

(5)

(6)

式中：r为曲率半径；θ为表面法线与水平线的夹角；δ为尖角高度；d为分层厚度.

(a) (b)

(c) (d)图10 参数曲面模型的适应性分层的层厚计算方法Fig.10 Calculation of adaptive slicing layer thickness based on parametric surface model

2.2 改进的适应性分层方法

目前, 大多数的适应性分层方法都是曲率计算法的衍生与改进[18].本文以尖角高度为控制参数, 对CAD模型直接切片.以图4中的鼠标模型为例, 介绍一种新的计算适应性分层切片厚度的方法, 适用于截面具有抛物线形状的零件.该方法不需要在分层轮廓处采样多个点处的曲率确定分层厚度, 也不需要根据采样点处的曲率用球面拟合零件表面的曲面, 从而简化计算.

根据理论分析和试验验证可知, 该鼠标模型两端的台阶效应最明显, 如图4所示.所以, 用过z轴且通过模型中轴线的平面与模型表面相交, 得到能够反映模型表面形状特征的且具有近似抛物线形状的参考曲线.根据该轮廓线曲率变化情况确定的分层厚度, 可以保证台阶误差最小.

首先考虑轮廓截面为半圆形的情况, 如图11所示, 分别推导出层厚的计算式为

(7)

(8)

式中:a为上一层的层厚;b为下一层的层厚;δ为尖角高度;r为曲率半径.

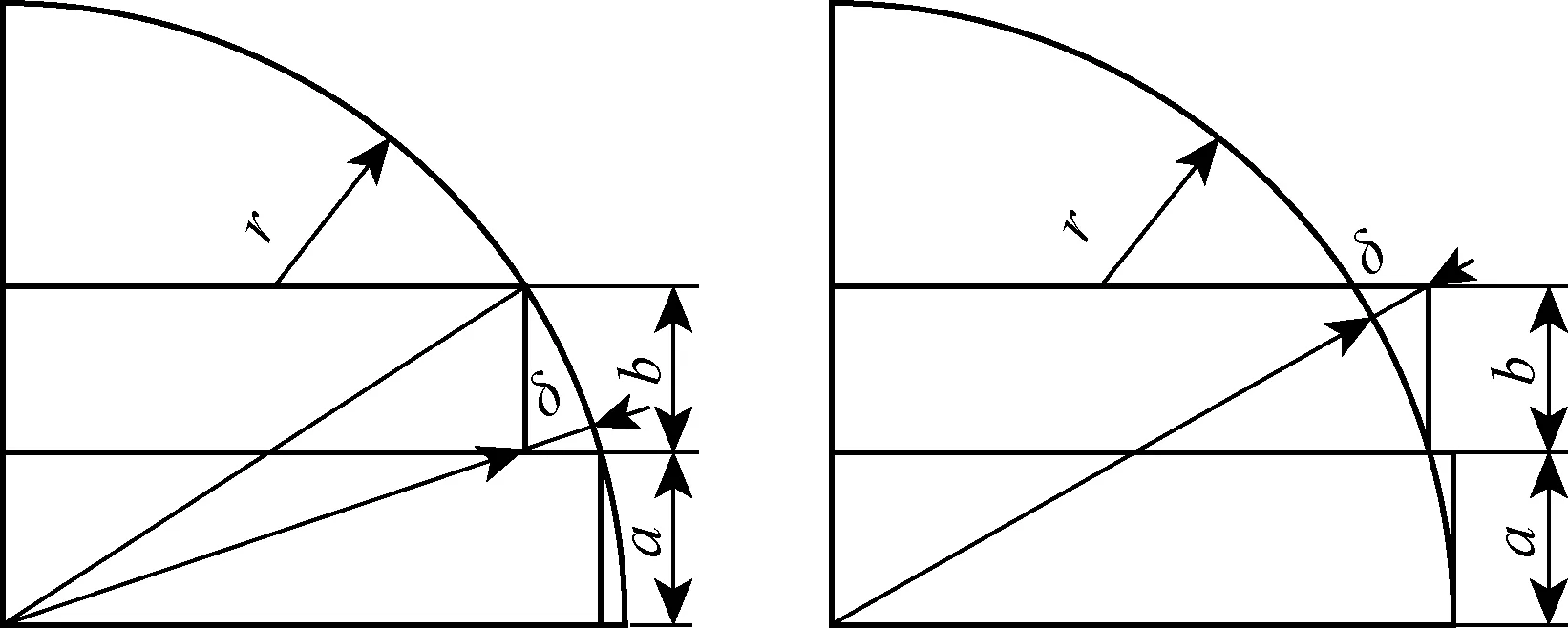
(a) (b)图11 半圆形截面轮廓层厚计算方法 Fig.11 Calculation of layer thickness based on semicircular cross-section contour

当截面轮廓为抛物线时, 如图12所示, 将台阶误差分为图12(a)所示的负偏差和图12(b)所示的正偏差两种情况.此时应该考虑轮廓各点处的曲率变化情况.

(a)

(b)图12 截面轮廓为抛物线时的层厚计算方法Fig.12 Calculation of layer thickness based on parabolic cross-section contour

根据图12所示, 由几何关系可分别推导出层厚b的计算式为

(9)

(10)

式中:R1与R2分别为对应点到原点O的距离;δ为尖角高度;a为上一层的层厚;b为下一层的层厚.

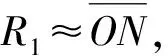
这样, 以尖角距离δ为控制参数, 给定一个切片厚度的取值范围, 便可以确定适应性分层的分层厚度.

3 适应性分层成型效率评价方法

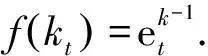
3.1 丝宽的计算模型[9, 20]

(11)

(a) (b)图13 FDM工艺的丝宽计算模型Fig.13 Calculation model of filament width in FDM process

由于从喷嘴中挤出丝的体积与堆积在已加工层上的丝的体积相等, 即

(12)

因此可近似求得丝宽计算式为

(13)

式中:ve为挤出速度;vf为填充速度;D为喷嘴孔直径;d为分层厚度;B为丝截面矩形区域的宽度;w为丝宽.

3.2 成型时间评价模型

根据体积相等的原则, 有

(14)

可推导出表示成型时间的数学模型为

(15)

式中:V体为成型件体积;m为出丝质量;ρ为丝材密度;B为丝截面矩形区域的宽度;d为分层厚度;vf为填充速度.

由式(15)可以看出, 成型时间与分层厚度、填充速度、丝宽和打印物体本身有关.层厚越小, 成型时间越长; 丝宽越大, 成型时间越短.所以, 在适应性分层时, 应考虑时间因素, 确定合理的分层厚度.

4 结 语

传统的曲率计算法需要在分层轮廓处采样多个点处的曲率, 然后用球面拟合零件表面.本文针对鼠标模型, 介绍了一种改进的分层厚度的计算方法, 即用通过模型中轴线的平面与模型表面相交, 得到能够反映模型表面形状的参考曲线, 根据参考曲线上曲率的变化情况确定分层厚度.该方法计算简单, 易于实现, 有效地减小了台阶效应对成型件表面质量的影响. 另外, 适应性分层方法不能忽视时间因素的影响.建立的成型时间的评价模型对快速成型制造具有一定的指导意义.

[1] ASTM International. F2792-12a Standard terminology for additive manufacturing technologies [S]. Pennsylvania: ASTM International, 2009.

[2] 骆锐, 吴沁. 基于三维CAD软件的快速成型制造技术及其精度控制[J]. 机床与液压, 2010, 38(4): 96-97.

[3] 赵吉宾, 刘伟军. 快速成型技术中分层算法的研究与进展[J]. 计算机集成制造系统, 2009, 15(2): 209-219.

[4] 郭新贵, 汪德才, 刘亚东, 等. 快速成型的切片数据优化[J]. 制造技术与机床, 2002(3): 30-32.

[5] 周惠群, 吴建军. 快速成型的STL模型切片轮廓优化新方法[J]. 制造业自动化, 2015, 37(6): 25-17.

[6] 刘伟军. 快速成型技术及应用[M]. 北京: 机械工业出版社, 2015: 36-38, 123.

[7] 吴晟, 罗宏保, 孙正烈. 快速成型的自适应分层研究[J]. 制造业自动化, 2007, 29(3): 93-95.

[8] 穆存远, 宋祥波. 快速成型台阶误差分析及其降低措施[J]. 机械设计与制造, 2011(4): 228-229.

[9] 张媛. 熔融沉积快速成型精度及工艺研究[D]. 大连: 大连理工大学机械工程学院, 2009.

[10] 王春香, 赵强. 快速成型中基于零件制造精度的分层算法优化[J]. 制造技术与机床, 2015(3): 22-25.

[11] 韩霞, 杨恩源. 快速成型技术与应用[M]. 北京: 机械工业出版社, 2012: 168-169.

[12] 张嘉易, 刘伟军, 王天然. 三维模型的适应性切片方法研究[J]. 中国机械工程, 2003, 14(9): 750-752.

[13] 胡汝霞. 基于RE/RP直接集成的模型切片处理方法研究[D]. 镇江: 江苏大学机械工程学院, 2005.

[14] DOLENC A, MAKELA I. Slicing procedures for layered manufacturing techniques [J]. Computer-Aided Design, 1994, 26(2): 119-126.

[15] 毕晓亮, 朱昌明, 侯丽雅. 快速成型中的自适应切片方法研究[J]. 计算机应用研究, 2002(4): 21-22.

[16] JAMIESON R, HACKER H. Direct slicing of CAD models for rapid prototyping[J]. Rapid Prototyping Journal, 1995, 1(2): 4-12.

[17] KULKARNI P, DUTTA D. An accurate slicing procedure for layered manufacturing [J]. Computer-Aided Design, 1996, 28(9) : 683-697.

[18] 蔡道生, 史玉升, 黄树槐. 快速成形技术中基于切片轮廓信息的自适应分层算法[J]. 机械科学与技术, 2004, 23(7): 849-851.

[19] 王雷, 钦兰云, 佟明, 等. 快速成型制造台阶效应及误差评价方法[J]. 沈阳工业大学学报, 2008, 30(3): 318-321.

[20] 邹国林. 熔融沉积制造精度及快速模具制造技术的研究[D]. 大连: 大连理工大学机械工程学院, 2001.

Adaptive Slicing Procedure for Rapid Prototyping Technology

FANXiao-liang,WANGJin-feng,LIChuan-shuai

(School of Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China)

In the fused deposition modeling process, staircase effect is directly caused by slicing procedure of 3D modeling. The staircase effect can reduce the surface quality of the parts. To reduce the step error, traditional method is to reduce the layer thickness and choose a reasonable slicing direction. It is hard that molding precision coordinates with molding efficiency in the traditional method. In order to solve the problem, an adaptive slicing procedure is introduced. The procedure firstly determines reference curves that can express surface shape of the model, and then select slicing thickness according to the changes of curvature in reference curve. The method is applicable to the parts that the contour line is of parabolic shape. And the method can insure molding precision and reduce the molding time. The evaluation model of the molding time are established, and the influence factors of the molding time are analyzed.

rapid prototyping; staircase effect; adaptive slicing; reference curve

1671-0444 (2016)04-0485-05

2016-03-31

国家自然科学基金资助项目(51301068)；教育部高等学校“专业综合改革试点”资助项目；河北省教育厅资助项目(Z2015127)；华北电力大学本科教育教学改革研究资助项目(13001403)

范孝良(1962—)，男，河北承德人，教授，硕士，研究方向为计算机集成技术、现代制造信息系统、工业工程等. E-mail: wcx803@163.com.

TH 16

A