基于灰色关联度的河南省高校创新人才多阶段综合评价权重优化

王洁方

(华北水利水电大学 管理与经济学院，河南 郑州 450046)

基于灰色关联度的河南省高校创新人才多阶段综合评价权重优化

王洁方

(华北水利水电大学 管理与经济学院，河南 郑州 450046)

河南省高校创新人才支持计划评价包括自评、网评和会评3个阶段，各阶段的评价结果通过权重进行集结，综合体现成果积分、网评专家、会评专家等的群决策结果。文章基于灰色关联分析方法分析阶段评价结果与综合评价结果的关联性，以及阶段权重设置对评价结果的影响，提出河南省高校创新人才多阶段评价的权重优化模型，并对2016年河南省高校创新人才多阶段评价数据进行了实证分析。

权重；创新人才；多阶段评价；优化

多阶段综合评价模型被广泛应用于创新项目、人才、团队等的评选。基于权重进行信息集结是多阶段综合评价模型协调各阶段群决策结果矛盾性的主要方法[1-3]。多阶段综合评价的权重确定方法包括专家赋权法等主观赋权法[4-5]，层次分析法、熵权法等客观赋权法[6-7]。

主观赋权法和客观赋权法各有优点，许多文献尝试将主观赋权法和客观赋权法相结合[9-11]。万俊等在得到决策者主观权重的基础上,提出一种权重调整算法，通过计算专家个体决策结果与群体决策结果的偏差量并结合熵理论，求得专家的客观权重,将其作为权重调整值[12]。笔者借鉴这些思想，结合河南省高校创新人才遴选评价的实际情况，用阶段评价排名与综合评价排名的灰色关联度方差最小化作为阶段评价权重的优化目标，提出多阶段综合评价的新型权重设置方法。

一、灰色关联度

设X0=(x0(1),x0(2),…,x0(n))为系统特征序列，X1=(x1(1),x1(2),…,x1(n))，…，Xi=(xi(1),xi(2),…,xi(n))，…,Xm=(xm(1),xm(2),…,xm(n))为相关因素序列。

式中：ξ为分辨系数，0<ξ<1，ξ取0.5；γ(X0,Xi)为X0与Xi的灰色关联度，反映系统特征序列与相关因素序列之间的接近程度。

二、河南省高校创新人才多阶段评价权重优化模型

为进一步加强高等学校学术带头人队伍建设，培养造就一大批拔尖创新人才，大力增强高等学校原始创新能力，持续提升高等学校的学术水平和人才培养质量，河南省教育厅、财政厅为加大“人才强校”工程建设力度，共同实施《河南省高校科技创新人才支持计划》。河南省高校创新人才按照自评、网评、会评3阶段顺次展开。3个阶段均按百分制计分，自评得分基于申请人的科研成果和数量累计得到，网评得分为若干名网络评审专家评分的均值，会评得分为会议评审专家现场评分的均值。最终依据3阶段评价结果的综合排名进行定额遴选。

记有n个申请人，自评、会评、网评3阶段得分分别为：

Y1=(y1(1),y1(2),…,y1(n))，

Y2=(y2(1),y2(2),…,y2(n))，

Y3=(y3(1),y3(2),…,y3(n))。

各阶段的初始权重向量

则n个申请人的综合评价得分

根据各阶段得分和综合得分，易得自评、会评、网评3阶段以及综合评价结果的排名向量分别为：

Z1=(z1(1),z1(2),…,z1(n))，

Z2=(z2(1),z2(2),…,z2(n))，

Z3=(z3(1),z3(2),…,z3(n))，

Z0=(z0(1),z0(2),…,z0(n))。

将Z0作为系统特征序列，Z1、Z2、Z3作为相关因素序列，灰色关联度γ1(Z0,Z1),γ2(Z0,Z2),γ3(Z0,Z3)反映综合评价结果与阶段评价结果的一致性。理想情况下，Z1、Z2、Z3高度一致，γ1(Z0,Z1),γ2(Z0,Z2),γ3(Z0,Z3)均趋近于1。实际上，各阶段评价的侧重点不同，成果积分、网评专家评分、会评专家评分可能发生矛盾。此时，若初始权重设置不合理，计算出的综合评价结果可能受某个阶段排名的影响过大，甚至出现被某阶段独裁的情况。体现在灰色关联度上，即该阶段评价结果排名与综合评价结果排名的灰色关联度过高，而与另外一些阶段的灰色关联度较低，3个阶段对应的灰色关联度计算结果的离散程度较大。

基于上述分析，应尽量调整自评、网评、会评3阶段的权重，使集结后的综合评价结果排名全面反映各阶段的评价排名。因此，记W=(w1,w2,w3)为调整后的权重，Δ1，Δ2，Δ3为权重调整量，则有

Δ1+Δ2+Δ3=0。

Δ1，Δ2，Δ3的取值应尽可能使3个阶段评价结果排名与综合评价结果排名的灰色关联度差异程度越小越好。方差反映灰色关联度的差异化程度。构建如下规划模型用于河南省高校创新人才阶段评估结果集结的权重优化。

X0=w1X1+w2X2+w3X3，

Δ1+Δ2+Δ3=0，

三、实证分析

对河南省2016年创新人才支持计划人口健康、数学管理信息、物理电子制造等3个大类6个组别的排名结果进行分析，测算出3个阶段评价结果排名顺序与综合评价结果排名顺序的灰色关联度见表1。

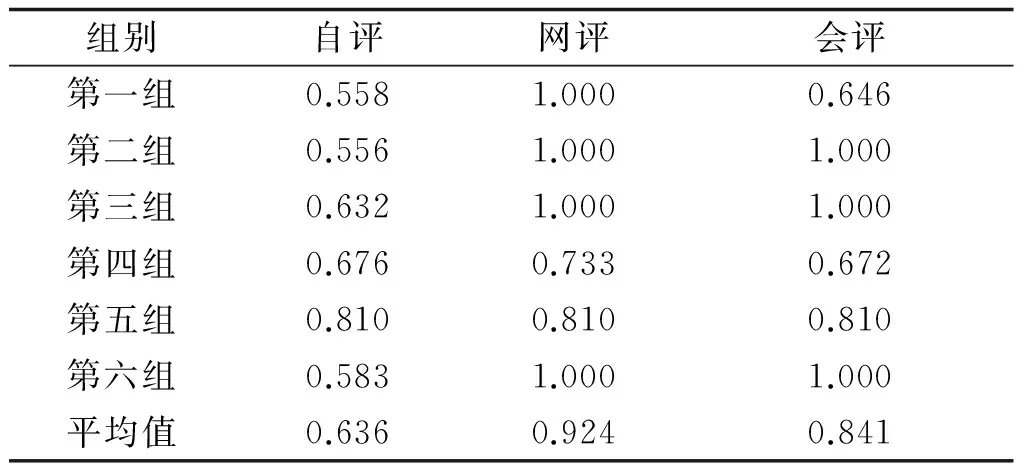
表1 2016河南省创新人才阶段排名与综合排名的灰色关联度

从表1可以得到，网评、会评、自评的排名与综合评价结果的灰色关联度依次降低。网评评价结果排名与综合评价结果排名的灰色关联度最高，为0.924，6组中有4组的灰色关联度达到1.000,综合排名被网评排名“独裁”的比例为66.7%，网评排名很大程度上决定了综合评价结果的排名。而自评排名与综合排名的灰色关联度平均值为0.636，作为一个唯一以客观定量积分形式的评价阶段，与综合排名的相关性最小，一定程度上降低了河南省高校科技创新人才评价的客观性。

2016年创新人才支持计划评审过程中，自评、网评、会评3阶段评价权重分别为5%、50%、45%。因此，记初始权重为W(0)=(5%,50%,45%)，由于表1中γ2(Z0,Z2)>γ3(Z0,Z3)>γ1(Z0,Z1)，设定权重调整方向应为Δ1>0,Δ2<0。而从适用性的角度考虑，权重变化Δ的量级可设置为1%。Δ1从0%到20%逐渐增加，目标函数的变化趋势如图1所示。

显然，综合评价结果排名随Δ1变化的规律是近似阶跃式的。

图1 权重优化目标函数随权重调整变化趋势

从图1可以看出，当9%≤Δ1≤13%时，3个阶段与综合评价结果的灰色关联度方差最小，综合评价结果有效体现了自评、网评、会评3个阶段的得分。基于尊重现状的原则，尽量保证评价政策的连续性，权重优化值应尽可能接近目标函数最小化的临界值(9%)，结合实用性原则，可取Δ1=10%，即w1=15%，此时w2=40%。因此，优化后的权重值为W=(15%,35%,45%)。

四、结语

在多阶段综合评价模式中，各阶段的评价内容具有不同的侧重点，综合评价结果应充分、公正地反映阶段评价结果。对于用于“排名优选”的多阶段评价模型，某个阶段排名不应独裁决定综合评价结果排名。笔者建立了以各阶段排名与综合阶段排名的灰色关联度方差最小化为目标的规划模型，用于权重优化。该模型应用于河南省高校创新人才3阶段评价权重优化，使创新人才的综合评价结果全面体现成果量化得分和专家意见。

[1] 周延年,朱怡安. 基于灰色系统理论的多属性群决策专家权重的调整算法[J]. 控制与决策,2012(7):1113-1116.

[2] 万树平. 基于Vague集的多属性群决策专家权重的确定[J].应用数学与计算数学学报, 2010(1):45-52.

[3] 梁樑,熊立,王国华. 一种群决策中专家客观权重的确定方法[J]. 系统工程与电子技术,2005(4):652-655.

[4] 蒋文能.群组决策中专家权重确定的思路和方法[J]. 统计与决策,2013(2):24-28.

[5] 周伟,何建敏,余德建. 直觉模糊群决策中专家权重确定的一种精确方法[J]. 控制与决策, 2013(5):716-720，725.

[6] 彭国甫,李树丞,盛明科. 应用层次分析法确定政府绩效评估指标权重研究[J]. 中国软科学,2004(6):136-139.

[7] 杨力,刘程程,宋利,等. 基于熵权法的煤矿应急救援能力评价[J]. 中国软科学,2013(11):185-192.

[8] 许叶军,达庆利. 基于理想点的多属性决策主客观赋权法[J]. 工业工程与管理,2005(4):45-47.

[9] 查奇芬,董洁,陈祖功. 主客观组合赋权法在科技成果转化评价分析中的应用[J]. 统计与决策,2009(16):152-154.

[10] 陈洪,赵建忠,刘勇,等. 基于集对论和主客观综合赋权法的装备保障能力评估研究[J]. 装备环境工程,2016(1):151-155，160.

[11] 万俊,邢焕革,张晓晖. 基于熵理论的多属性群决策专家权重的调整算法[J]. 控制与决策,2010(6):907-910.

(责任编辑：蔡洪涛)

Weight Optimization of Multi Stage Comprehensive Evaluation of University Innovative Talents in Henan Based on Grey Correlation Degree

WANG Jiefang

(School of Management and Economics, North China University of Water Resources and Electric Power, Zhengzhou 450046,China)

Innovation Talents in Universities of Henan Province support plan evaluation including three separate stages, such as self-assessment, network assessment and meeting review. Each stage evaluation results through the weights for the aggregation, which comprehensively reflect the achievement score, network and meeting assessment experts’ decision results. Based on grey relational analysis method, stage evaluation results and the comprehensive evaluation results of the correlation analysis, and the phase weights setting influence on the evaluation results are researched. The weight optimization model of multi stage comprehensive evaluationof university innovative talents in Henan is put forward. An empirical analysis of the multi stage evaluation data of university innovation talents in Henan province in 2016 is carried out.

weight; innovative talents; multi stage evaluation; optimization

2016-10-08

河南省高等学校重点科研项目“高等学校科技人才绩效管理研究”(15A630040)、“高等学校科技成果管理模式研究”(15A630073)、“高等学校科技管理创新模式研究”(15A630005)、“河南省高等学校科研经费配置评价及优化系统构建”(15A910003)；河南省科技厅重点科技攻关项目“河南省高校协同创新平台管理模式研究”(142102310123)

王洁方(1982—)，女，河南洛阳人，华北水利水电大学管理与经济学院副教授，博士，研究方向为系统评价方法与科技管理。

G526.3

A

1008—4444(2016)06—0015—03