动态代谢组学数据分析方法介绍*

哈尔滨医科大学公共卫生学院卫生统计学教研室（150081） 王文佶 张秋菊 曲思杨 谢彪 高兵 孙琳 刘美娜

动态代谢组学数据分析方法介绍*

哈尔滨医科大学公共卫生学院卫生统计学教研室（150081） 王文佶 张秋菊 曲思杨 谢彪 高兵 孙琳 刘美娜△

近年来，代谢组学发展迅速并广泛应用于营养学、毒理学、疾病诊断等各个领域［1］。随着研究的深入，代谢组学所获得的数据集因研究设计的不同而日益复杂，产生了有时间间隔的动态代谢组学数据。然而目前分析此类数据的方法十分有限，并且在大多数情况下，这种动态数据所带来的因时间因素产生的变异直接被忽略。据此，本文回顾了现有的动态代谢组学数据的分析方法并对其研究进展进行介绍。

常用代谢组学数据分析方法

代谢组学数据最大特点是变量数远远大于观测数，且变量之间存在着高度相关性。目前，最常用于代谢组学数据分析的方法有：无监督学习方法的主成分分析（PCA）［2］、有监督学习方法的偏最小二乘判别分析（PLS-DA）［3］、正交偏最小二乘判别分析（OPLSDA）等［4］。这些方法可以提取原始信息的最大变异或在此基础上的最佳解释变异，将高维数据映射到低维空间，并给出降维后数据的可视化展示。随着研究深入，代谢组学不再拘泥于横断面研究，包含时间因素的动态代谢组数据被越来越多的研究所获得，这使得传统分析方法不再适用［5］。以PCA为例，来说明传统分析方法不再适用动态代谢组学数据分析的原因。

在动态代谢组学研究中，其数据特点不止是小样本大变量所带来的高维性，数据中还存在与时间有关的变异。例如：研究某种干预（药物，毒物等）随着时间改变对不同处理组产生的效应是否有差别，并感兴趣于找出随时间改变的差异代谢物。若以矩阵每一行代表代谢组学数据每一个样本的观测时间点，列代表代谢产物进行PCA，在不断进行行间打乱后，会发现原始得分矩阵Z始终等同于打乱后的得分矩阵Zr，原始载荷矩阵P0始终等同于打乱后的载荷矩阵这说明PCA盲于观测之间因时间因素产生的自相关变异，若生硬地把所有时间点的数据同时进行主成分分析，只是一味地提取原始信息的最大变异进行降维而忽视变异的来源，将导致与时间相关的变异成为混杂因素而混淆处理因素带来的差异。这就是传统PCA、PLS-DA、OPLS-DA不能解决动态代谢组学的关键。此时，迫切需要一类代谢组学数据的分析方法，可以在降维的同时捕捉到时间趋势产生的变异，更真实地揭示数据之间内部结构——动态代谢组学数据分析方法。

动态代谢组学数据分析方法

本文主要从降维的角度对动态代谢组学数据分析方法进行归纳介绍，包括以下方法：动态主成分分析、动态偏最小二乘法、方差同步主成分分析以及动态概率主成分分析方法等。从模型的发展来源、基本原理、适用情况及优缺点等方面介绍。

1．动态主成分分析

动态PCA模型包括两种形式，第一种是由Ku等人1995年提出的动态PCA［7］，第二种由Timmerman等人在2001年提出的滞后PCA［8］，区别在于前者是对X矩阵进行二次变换，后者是对得分矩阵进行二次变换。其基本思想是：每个观测在每一个时间点所测得的代谢物浓度（位移）不仅由本时间点的测量所决定，还受之前时间点影响。所以动态PCA可以看成是自回归滑动平均外生（ARMAX）的时间序列模型与PCA模型的结合［9］。定义二次变换矩阵Bl＝［0T×（L－l）｜IT｜0T×l］，l＝0，…，L代表时间滞后，X为（（T+L）×J）的矩阵。下面以L＝2来阐述动态PCA的工作原理。

新矩阵实质上是一个三维矩阵，包含三种变异：不同变量（代谢产物）之间的变异；相同变量不同时间点间的变异；不同时间点以及不同变量间的变异［10］。因此对矩阵进行PCA分析后，得到的是这三种变异的混合得分。

动态PCA的一个局限是：由于把X矩阵分割成了各个部分，降低了在时间方向上样本的数量，导致随着时间点增多丢失的信息随之增加。另一种可选择的三维矩阵分析方法是PARAFAC或Tucker3模型［10］，这两类模型没有对变量进行滞后变换，一定程度上解决了动态PCA因多次滞后变换导致信息丢失的问题。Rubingh等人利用PARAFAC和N-PLS对微生物发酵过程中细胞代谢产物进行动态分析，得到了发酵的两个不同的阶段，识别出随着时间变化，诱导大肠杆菌产生苯丙氨酸的代谢物［11］。

此外，PCA的扩展模型还包括2004年Jansen等人提出的加权PCA［12］，其基本思想是：根据代谢物同一时间点测量值的变异大小匹配不同的权重，除去了测量误差的影响，凸显代谢物在时间上的波动性。2009年Jansen等人在一篇关于植物代谢组学研究中［13］，提出局部PCA模型：先对所有时间点进行整体的PCA分析，再把每个时间点的变量应用局部PCA模型，最后利用交叉适应分析（cross fit analysis）将几个模型不同时间点联系起来作为动态分析结果解释。

2．动态偏最小二乘法

这里介绍三种动态偏最小二乘法：

第一种方法是有限脉冲序列模型，1987年Ljung等人在系统识别应用中提出［14］。该方法首先对X矩阵进行时间滞后变换，然后将滞后的x变量作为一个新矩阵与表型y进行偏最小二乘分析（PLS）。以此模型为基础，1996年Qin等人在滞后变量x的基础上同时滞后变量y，再进行建模分析，对该模型进行了扩展［15］。然而，基于代谢组学数据小样本多变量的特点，这两种方法使得原本已经庞大的X矩阵，在不断被滞后变量扩展后变得更为庞大，导致低样本量带来的问题进一步加剧，且增大的载荷矩阵让模型很难解释，无法挖掘潜在的数据结构［16］。此时PLS虽有着较好的降维能力，但与其带来的缺点相比，此方法并不可行［16］。

第二种方法于1993年由Kaspar和Ray等人在过程控制中提出［17］。该方法的核心是利用先验的动态信息定义了一个动态“过滤器”，将滤过的X矩阵与y建立PLS模型。这种方法不存在上述X维度突长的问题，但在代谢组学中，对这样敏感的“过滤器”的调节是一件艰巨而又复杂的任务。

第三种方法为批次建模（batchmodeling），于1998年由Wold等人提出。此方法最早应用在化工领域来监视批次生产过程［18］。方法的基本思想是把时间当做一个额外的变量参与建模，所研究数据往往是三个维度，各个维度分别代表：观测对象、变量、样本的时间点。Antti等人用该方法在小鼠尿液核磁共振组学的研究中［19］，得到肝毒素动物模型中与时间有关的代谢变化。该方法的缺点是所有的研究对象必须有类似的代谢变化和反应速率。此外，2008年Rantalainen等人提出了另一种处理代谢组学时间序列数据的新方法——分段多元建模［20］，该方法保留了正交偏最小二乘的特点，并且可以描述相邻时间点的差异，但若两个相邻时间点代谢物的差异较小，或取样的频率较高时，该方法变得不再适用。

3．方差同步主成分分析（ANOVA-simultaneous component analysis，ASCA）

处理动态数据时也可选用方差分析（ANOVA）模型，模型中时间因素可以以定性或定量的方式来估计［21］。定性分析是指时间因素被当成一个定性变量拟合至模型中，从而得到时间效应。定量分析是指时间因素被当成一个定量变量以线性、二次方或曲线的形式拟合到模型中。在有关基因表达的文献中，我们可以看到时间因素被定性和定量拟合的实例［22－23］。

由于ANOVA只适合单一的生物反应，在面对代谢组学的高通量数据时，忽略了代谢产物之间的高相关性，因此不再适用。关于ANOVA方法的扩展层出不穷，1979年Mardia等人提出多元方差分析模型（multivariate-ANOVA，MANOVA）［24］，但因代谢组学数据协方差矩阵的奇异性使得该方法步履维艰。2004年Smilde等人提出方差同步主成分分析（ANOVA-simultaneous component analysis，ASCA）［25］，把数据集分解成效应矩阵同时进行降维分析。以基于实验设计、考虑时间因素的代谢数据为例，ASCA首先将总变异分解成三个来源：时间因素，时间因素与处理因素的交互效应，以及不同个体间的变异。分别对这三部分矩阵进行主成分分析，得到随着时间的改变各部分效应的得分变化趋势图，从而给出合理的生物学解释。Smilde等人在一篇关于代谢组学干预研究中利用ASCA模型检验了维生素C对几内亚猪骨关节炎进展中的作用［25］。此外，ASCA模型已成功应用到心理测量学［26］、蛋白质组学［27］、以及化学计量学［28］。

ASCA模型还可以与平行因子分析（PARAFAC）相结合，即PARAFASCA模型，与ASCA相比，PARAFASCA模型在描述因实验设计带来的交互效应时更加简洁易懂［29］。此外，ASCA没有限定时间因素必须为线性，Sm ilde等人用其扩展的方法捕捉非线性时间的变化［30］。需要注意的是我们这里说ASCA是一种动态的方法，其前提是时间因素被定量地拟合到模型中［6］。

4．动态概率主成分分析（dynamic probabilistic principal components analysis，DPPCA）

在代谢组学的数据分析中，不论是适合横断面分析的传统PCA，还是基于代谢组学实验设计，考虑时间因素所扩展的动态PCA模型、加权PCA、局部PCA、ASCA模型，从方法的角度来说，它们都不是一个相应的生成概率模型，因此很难评价在拟合模型估计时的不确定性；从应用的角度来说，纵向代谢组学研究更关注的是处理因素对代谢物在时间效应上的影响，找出真正随时间变化有显著意义的代谢产物，从而挖掘出更多的生物学信息，给出更科学合理的生物学解释，而上述方法都在模型的解释性上略显贫乏。据此，2013年Nyamundanda等人提出动态概率主成分分析（DPPCA），并结合线性混合模型（linearm ixed model，LMM）［31］完美解决了上述问题［1］。

DPPCA模型实质上是概率主成分分析（probabilistic principal components analysis，PPCA）［32］与随机波动模型（stochastic volatility，SV）［33］的结合。前者主要用于数据降维和分析数据中变量的变异，后者假设变量在各时间点间存在一阶自回归过程，分析由于重复测量而产生的时间变异。PPCA由Tipping和Bishop在1999年基于高斯潜变量模型提出［32］，模型表达式为：xi＝W ui+εi（W是载荷矩阵，ui是潜变量，εi是误差项）。它将主成分分析理论放在概率框架中进行讨论，给出了数据信息在主子空间表达时所对应的概率密度估计。

DPPCA模型的构建原理为：假设PPCA模型中潜变量ui和误差εi满足随机波动模型，观测在时间点m的p个观测变量xim的DPPCA模型表达式如下所示：

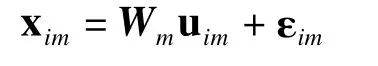
Wm为载荷矩阵为潜在得分，且Wm和随着时间而变化。然后分别对DPPCA的潜变量uim和误差εim建立SV模型，得到个体i（i＝1，…，n），主成分j（j＝1，…，q），时间点m（m＝1，…，M），潜变量uijm的SV模型以及观测i在时间点m的p维向量的误差项的SV模型。

纵向代谢组学数据利用DPPCA模型，实现了以下至关重要的几点：首先在数据可视化上，DPPCA在降维的空间里给出不同处理组的主成分随时间改变的轨迹。其次，DPPCA可以评价不同处理组的时间效应，通过后验分布的载荷大小得到不同处理组最具影响力的代谢物清单。最后利用线性混合模型在这些最具影响力的代谢产物中，识别浓度随时间变化而变化显著的物质。2013年Nyamundanda等人利用DPPCA模型找到了在给药组和对照组随着时间的改变，代谢趋势相反的代谢产物［32］。

5．其他方法：

除上述降维的方法外，2006年Tai和Speed提出多元贝叶斯时间序列分析法应用于基因芯片的时间序列分析中［34］，Metaboanalyst网站（http：//www．metaboanalyst．ca）基于该方法的改进给出了时间序列代谢组学的实现途径［35］，模型按照随着时间改变，组间差异最大的顺序得到代谢产物的排名清单。2011年Berker等人构建了一个适合短时间序列的代谢组学数据分析框架［36］，通过平滑样条混合效应（smoothing splinem ixed effects，SME）模型，使观测的每个时间序列被视为潜在的随机分布或平滑曲线被估计，最后用一个函数统计量来检验两组曲线的差别，从而找出随时间改变不同组间的差异代谢物。此外，聚类算法也被应用于时间序列数据分析中［37－38］，实现通过动态变化来进行特征分组，读者有兴趣可以自行查阅。

小 结

动态代谢组学数据不同于横断面研究数据，其数据集的变异来源更加复杂。传统PCA只能提取数据集的最大变异而无视变异的来源，与时间有关的变异会成为一个混杂因素混淆处理因素的作用，因此选择一种动态代谢组学数据的分析方法尤为必要。本文主要从降维的角度对动态代谢组学数据分析方法进行回顾与介绍，揭示时间效应对生物代谢的影响。

在选择一种动态分析模型时应考虑实验设计所涉及的时间点的个数、时间的间隔、所测得的代谢物的数量。可以根据研究设计和目的不同选用加权PCA，局部PCA批次模型从不同角度解释时间带来的变异性。若想检验数据不同来源的变异随时间的变化趋势可选用ASCA模型；若研究关注随时间改变不同处理组的差异代谢产物可选用DPPCA和混合线性模型；另外，多时点的动态代谢组学数据慎重选用动态PCA避免因时间点增多丢失的信息逐渐增加。

由于此类方法在降维的同时需要考虑时间因素的变异，使得模型难构建且可能涉及多个模型的结合问题，导致分析方法和分析技术的复杂性增加，限制了该类方法的广泛应用。一种简洁而有效的模型亟待开发，值得更多的生物统计学者的研究与关注。一个合适的动态代谢组学数据分析方法可以挖掘出数据潜在的更真实、有价值的信息，对健康、疾病有关的生物节律的探索有着重要意义。

［1］Nyamundanda G，Gorm ley IC，Brennan L．A dynam ic probabilistic principal componentsmodel for the analysis of longitudinalmetabolom ics data．Journal of the Royal Statistical Society：Series C（Applied Statistics），2014，63（5）：763-782．

［2］Bro R，Sm ilde AK．Principal component analysis．Analytical Methods，2014，6（9）：2812-2831．

［3］Westerhuis JA，Hoefsloot HCJ，Sm it S，et al．Assessment of PLSDA cross validation．Metabolom ics，2008，4（1）：81-89．

［4］Boccard J，Rutledge DN．A consensus orthogonal partial least squares discrim inant analysis（OPLS-DA）strategy formultiblock Om ics data fusion．Anal Chim Acta，2013，769：30-39．

［5］Sm ilde A．Analysis of High-dimensional Data from Designed Metabolom ics Studies．Metabolic Profiling：Disease and Xenobiotics，2014，21：117．

［6］Sm ilde AK，Westerhuis JA，Hoefsloot HC，et al．Dynam ic metabolom ic data analysis：a tutorial review．Metabolom ics，2010，6（1）：3-17．

［7］Ku W，Storer RH，Georgakis C．Disturbance detection and isolation by dynam ic principal component analysis．Chemometrics and intelligent laboratory systems，1995，30（1）：179-196．

［8］Timmerman ME．Component analysis of multisubject multivariate longitudinal data．Ph D thesis，University of Groningen，2001．

［9］Chen J，Liu K．On-line batch processmonitoring using dynam ic PCA and dynam ic PLS models．Chem ical Engineering Science，2002，57（1）：63-75．

［10］Sm ilde AK，Hendriks MM，Westerhuis JA，et al．Data Processing in Metabolom ics．Metabolom ics in Practice：Successful Strategies to Generate and Analyze Metabolic Data，2013：261-284．

［11］Rubingh CM，Bijlsma S，Jellema RH，et al．Analyzing longitudinal microbialmetabolomics data．J Proteome Res，2009，8（9）：4319-4327．

［12］Jansen JJ，Hoefsloot HCJ，Boelens HFM，et al．Analysis of longitudinalmetabolomics data．Bioinformatics，2004，20（15）：2438-2446．

［13］Jansen JJ，van Dam NM，Hoefsloot HCJ，etal．Crossfitanalysis：a novelmethod to characterize the dynamics of induced plant responses．BMC Bioinformatics，2009，10（1）：1．

［14］Ljung L．System identification．New Yersey：Prentice Hall，1987，163-173．

［15］Qin SJ，McAvoy TJ．Nonlinear FIR modeling via a neural net PLS approach．Comput Chem Eng，1996，20（2）：147-159．

［16］Dong Y，Qin SJ．Dynamic-Inner Partial Least Squares for Dynamic Data Modeling．IFAC-PapersOnLine，2015，48（8）：117-122．

［17］Kaspar MH，Ray WH．Dynamic PLSmodelling for process control．Chemical Engineering Science，1993，48（20）：3447-3461．

［18］Wold S，Kettaneh N，Fridén H，et al．Modelling and diagnostics of batch processesand analogous kinetic experiments．Chemometricsand intelligent laboratory systems，1998，44（1）：331-340．

［19］Antti H，Bollard ME，Ebbels T，et al．Batch statistical processing of 1H NMR-derived urinary spectral data．JChemom，2002，16（8-10）：461-468．

［20］Rantalainen M，Cloarec O，Ebbels TMD，et al．Piecewisemultivariate modelling of sequentialmetabolic profiling data．BMC Bioinformatics，2008，9（1）：105．

［21］Searle SR．Linear Models．New York：JW iley＆Sons，1971．

［22］Storey JD，Xiao W，Leek JT，et al．Significance analysis of time coursem icroarray experiments．Proc Natl Acad Sci USA，2005，102（36）：12837-12842．

［23］Conesa A，Nueda M J，Ferrer A，et al．maSigPro：amethod to identify significantly differential expression profiles in time-coursem icroarray experiments．Bioinformatics，2006，22（9）：1096-1102．

［24］Mardia KV，Kent JT，Bibby JM．Multivariate analysis．New York：Academ ic Press，1980．

［25］Sm ilde AK，Jansen JJ，Hoefsloot HCJ，et al．ANOVA-simultaneous component analysis（ASCA）：a new tool for analyzing designed metabolom ics data．Bioinformatics，2005，21（13）：3043-3048．

［26］Timmerman ME，Kiers HAL．Four simultaneous componentmodels for the analysis ofmultivariate time series from more than one subject to model intraindividual and interindividual differences．Psychometrika，2003，68（1）：105-121．

［27］Harrington PdB，Vieira NE，Espinoza J，et al．Analysis of varianceprincipal component analysis：A soft tool for proteom ic discovery．A-nal Chim Acta，2005，544（1）：118-127．

［28］de Noord OE，Theobald EH．Multilevel component analysis and multilevel PLS of chem ical process data．J Chemom，2005，19（5-7）：301-307．

［29］Jansen JJ，Bro R，Hoefsloot HCJ，et al．PARAFASCA：ASCA combined w ith PARAFAC for the analysis ofmetabolic fingerprinting data．JChemom，2008，22（2）：114-121．

［30］Sm ilde AK，Hoefsloot H，Westerhuis J．The geometry of ASCA．J Chemom，2008，22（8）：464-471．

［31］Mei Y，Kim SB，Tsui K．Linear-mixed effectsmodels for feature selection in high-dimensionalNMR spectra．Expert Systemswith Applications，2009，36（3）：4703-4708．

［32］Tipping ME，Bishop CM．Probabilistic principal component analysis．Journal of the Royal Statistical Society：Series B（Statistical Methodology），1999，61（3）：611-622．

［33］Jacquier E，Polson NG，Rossi PE．Bayesian analysis of stochastic volatility models．Journal of Business＆Economic Statistics，2002，20（1）：69-87．

［34］Tai YC，Speed TP．A multivariate empirical Bayes statistic for replicated microarray time course data．The Annals of Statistics，2006，34（5）：2387-2412．

［35］Xia J，Mandal R，Sinelnikov IV，et al．MetaboAnalyst2．0-a comprehensive server for metabolomic data analysis．Nucleic Acids Res，2012，40（W1）：W127-W133．

［36］Berk M，Ebbels T，Montana G．A statistical framework for biomarker discovery in metabolomic time course data．Bioinformatics，2011，27（14）：1979-1985．

［37］Wang J，Liu P，She MFH，et al．Biomedical time series clustering based on non-negative sparse coding and probabilistic topic model．ComputMethods Programs Biomed，2013，111（3）：629-641．

［38］Wang K，Ng SK，M cLachlan GJ．Clustering of time-course gene expression profiles using normal mixture models with autoregressive random effects．BMC Bioinformatics，2012，13（1）：1．

（责任编辑：郭海强）

*国家自然基金（81502889）；黑龙江省自然基金重点项目（ZD201314）

△通信作者：刘美娜，E-mail：liumeina369＠163．com