竞争风险型数据统计分析理论研究进展

国家癌症中心/中国医学科学院北京协和医学院肿瘤医院（100021） 杨 召 王少明 梁 赫 乔友林 范金虎

·综述·

竞争风险型数据统计分析理论研究进展

国家癌症中心/中国医学科学院北京协和医学院肿瘤医院（100021） 杨 召 王少明 梁 赫 乔友林 范金虎△

在医学随访研究中，受试者在观察期间常常由于出现其他结局事件而阻碍目标结局事件的发生或改变目标结局事件发生的概率。例如，在人群原因别死亡率的研究中目标结局事件为肿瘤相关死亡，但随访过程中常出现心脑血管相关死亡而阻止了肿瘤相关死亡事件的发生，即竞争风险（competing risk）［1］。在此理论框架下可能出现：（1）目标结局事件（event of interest）；（2）竞争事件（competing event）；（3）删失事件（cersored）。竞争风险在医学研究中十分普遍［2－5］，其最早可以追溯到1760年伯努利接种“疫苗”根除天花对人群死亡率的影响［6］。

本研究系统性地回顾竞争风险型数据的分析方法，主要从下面几个方面对其研究进展进行系统性的描述：（1）竞争风险（competing risk）的定义；（2）常见竞争风险型数据分析方法的简介：原因别风险模型（cause－specific hazard model）、累积风险模型（subdistribution hazard model）、加性模型（additivemodel）、基于虚拟观测的回归模型、混合模型（mixture）和纵向模型（verticalmodel）；（3）竞争风险型数据统计分析的研究进展。

竞争风险型数据

在随访研究中，目标结局事件短时间内可能无法确定，因此为了评价研究因素对特定人群中目标结局事件的影响，所有受试者从基线开始随访，到发生目标结局事件或试验结束。若随访期间未观察到受试者出现目标结局事件则被定义为删失（censored），如失访（lost to follow－up），且在经典的生存分析中假设删失为“非信息性删失（non－informative censored）”，即相同条件下受试者在某时刻发生删失事件的概率和发生结局事件的概率相等［7］。若随访期间，受试者只出现目标结局事件，则可以通过经典的分析方法，如KM法［8］和Cox等比例风险模型［7］进行分析，详见图1a。若随访期间出现多个结局事件，则为竞争风险［1］，其根据对目标结局事件的影响程度分为两类：

1.经典竞争风险（classical competing risk）

经典的竞争风险，指随访期间受试者出现多种互斥结局事件，即某一结局事件的发生常阻止其他结局事件的发生，详见图1b。譬如，在人群死亡研究中，若受试者出现肿瘤相关的死亡，则不会出现心脑血管疾病相关的死亡；反之亦然。

2.半式竞争风险（semi-competing risk）

半式竞争风险，也叫状态转移风险，指随访期间受试者由于出现其他结局事件而导致目标结局事件出现的概率发生改变，详见图1c。例如，在乳腺癌预后研究中，若目标结局事件为死亡，则受试者可能会因为出现复发转移而使其死亡的风险发生改变。

图1 竞争风险型数据模式图（λi为风险函数）

与经典的生存分析方法相同，竞争风险模型数据的分析主要从以下三个方面：（1）时间效应，即目标结局事件的发病率如累积发病率（cumulative incidence）或发病密度（incidence densities）；（2）干预效应，即不同干预措施对目标结局事件发病率的影响；（3）存在混杂因素时，干预因素对目标结局事件的累积发病率的影响。

竞争风险型数据的常用统计分析方法

为了能够更加清晰明了地介绍下述常见竞争风险型数据的统计分析方法，做出以下假设：随访过程中会出现2个竞争事件（J，J＝1提示发生结局事件1；J＝2提示发生结局事件2），则该研究中所收集得到的竞争风险型数据为｛ti，εi，εi×J，Xi｝，其中：ti为第i名受试者的最短观察时间ti＝min（TiJ＝1，TiJ＝2，Ci）；εi为第i名受试者是否出现结局事件（εi＝1，发生结局事件；εi＝0，未发生结局事件）；εi×J为第i名受试者发生结局事件的类型（εi×J＝1，发生结局事件1；εi×J＝2，发生结局事件2）；Xi为第i名受试者协变量的状态。那么，受试者发生结局事件的风险函数（hazard function）为λ（t）；生存函数（survival function）为S（t）；累积发病率函数（cumulative incidence function，CIF）为F（t）。

在经典的生存分析中，统计学家将干预因素对目标结局事件发病率/死亡率的影响，通过Kaplan-Meier经验估计法转化为干预因素对目标结局事件发生风险的影响，即：将原始无效假设H0：F（g＝1）（t）＝F（g＝2）（t）转化为H0′：λ（g＝1）（t）＝λ（g＝2）（t）或H0′：S（g＝1）（t）＝S（g＝2）（t）。这种转化在竞争风险理论中却不是等价的［9］。下文将着重从风险函数、生存函数和累积发病率函数的角度介绍几种常见的竞争风险型数据分析方法：

1.风险函数为基础的分析方法

（1）原因别风险模型（cause-specific hazard model）

原因别风险模型，作为Cox等比例风险模型的衍生模型，最早由Prentice［10］引进到竞争风险型数据的分析中，随后在争议中迅速发展并得到广泛的应用［1］。该理论直接将竞争结局事件定义为删失事件，然后依次对每个结局事件轮流拟合经典的Cox等比例风险模型。此时，t时刻发生目标结局事件j风险函数

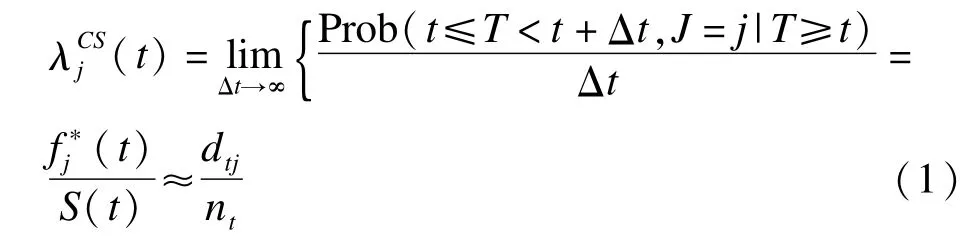
则t时刻的总体生存函数SCS（t）和t时间内累积发病率函数分别为：

当存在干预因素时，该模型与经典分析方法一样需要做出以下假设：（1）干预因素对目标结局事件的影响不随时间的变化而改变，即满足等比例风险假设（proportional hazard assumption，PHA）；（2）各结局事件之间的发生互不影响，即独立性。根据经典Cox等比例风险模型［7］的定义，则原因别风险模型即为：

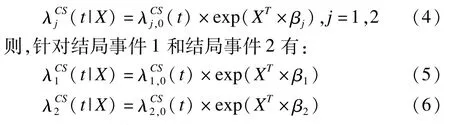
为了能够直观形象地描述协变量与目标结局事件发生风险，exp（βj）＝HRCS表示协变量每改变1个单位结局事件j发生风险的变化。此时，该模型不能直接评价协变量对目标结局事件累积发病率影响，究其原因主要是因为：结局事件1的累积发病率函数不仅仅与结局事件1的原因别风险函数有关系，而且与结局事件2的原因别风险函数有关系。当结局事件1的原因别风险函数增加时，其累积发病率函数不一定增加；反之亦然［9］。因此，原因别风险模型不能直接用来评价竞争风险型数据中目标结局事件的累积发病率；当利用HRCS描述协变量与目标结局事件发生风险之间的关联时，需谨慎下结果。此外，该模型中回归系数的估计采用部分似然函数（partial likelihood function）用最大似然估计方法得到，对模型的假设检验常采用似然比检验（maximum likelihood ratio test），其拟合过程可以借助标准统计分析软件包如SAS、R或SPSS实现。当存在时依性协变量时，该模型和Cox模型一样可拓展为时依性协变量的原因别风险模型（time－dependent causespecific hazard model），具体理论介绍详见［11］。

（2）累积风险模型（subdistribution hazard model）

考虑到原因别风险模型存在前提假设严格且不能直接估计竞争风险型数据中目标结局事件累积发病率等缺点，Fine和Cray［12］提出利用累积风险模型直接估计协变量对目标结局事件累积发病率的影响。该理论充分考虑了竞争风险事件对目标结局事件的影响，其定义t时刻目标结局事件j的风险函数

则，t时间内目标结局时间j的累积风险函数与经典生存分析相同：

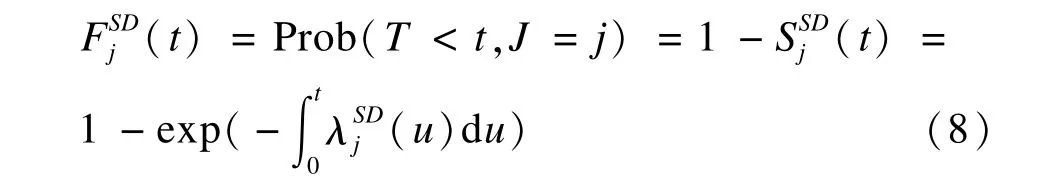
当存在干预因素或协变量时，该模型也需要满足等比例风险假设和非信息性删失。此时，累积风险模型为：

（3）加性模型（additivemodel）

在经典的竞争风险理论假设中，结局事件之间的发生是互斥事件。Klein［13］参照Aalen加性模型提出各结局事件之间的累积发病率具有可加性，则在累积风险模型中，定义t时间内结局事件j＝｛1，2｝的累积发病率（详见公式（8））分别为：

根据加性模型理论，结局事件j＝｛1，2｝在t时间内的累积发病率函数为：

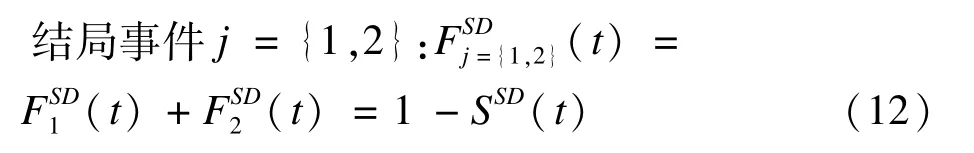
当存在协变量时，根据累积风险模型理论：

式中，g（·）为转换函数。若进一步将公式（14）代入（12）：

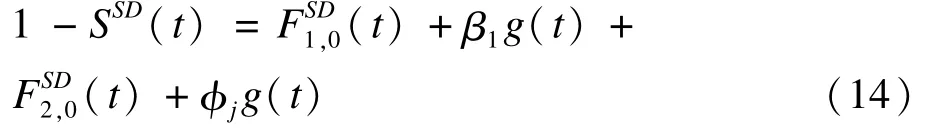
此时，在公式（14）中出现了悖论，即在t＝0时刻，公式两侧是不相等的。但是，该加性模型同时将各个竞争事件纳入同一个模型中进行研究，可以直观地比较协变量同时对多个结局事件的影响。该模型多采用偏似然估计法（partial likelihood approach）进行拟合，且可以在R中“survival”软件包实现。此外，实际应用中研究者更注重协变量对目标结局事件远期的影响［1］。

2.虚拟观测（pseudo－observations）为基础的分析方法

Andersen［14－15］认为竞争风险本质上为多状态模型的一种特殊形式，其将原因别风险看作为转移风险，并引入潜在失效时间的分析方法。其主要思想是构造虚拟观测替换删失个案，然后通过广义线性模型拟合协变量对目标结局事件的影响。该理论定义t时间内目标结局事件j累积发病率函数为

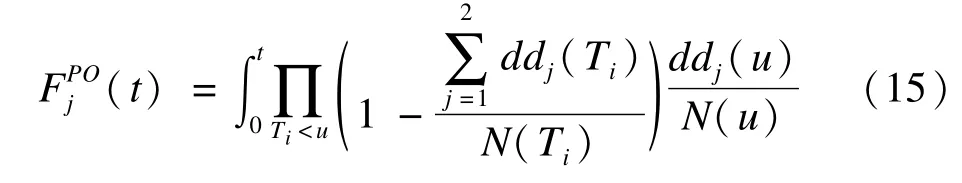
若假设随访期间有i＝｛1，2，…，n｝个删失观测，随访时间点为τt＝｛τ1，τ2，…，τT｝，则虚拟观测定义为：

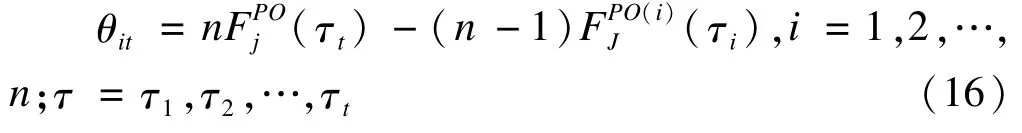
其中，θit为τt时刻第i个删失的虚拟观测值，则分别为τt时间内结局事件j的累积发病率函数、剔除删失事件i之后τt时间内结局事件j的累积发病率函数。当不存在删失事件时，可以按照经典广义线性模型的方式分析各个协变量对目标结局事件的影响。定义连接函数g（·）为logit函数，则在协变量X存在情况下，虚拟观测是否发生结局事件的拟合过程即为多元logistic回归分析的过程：

此时，针对各协变量对结局事件影响的解释与logistic回归分析相同。此外，Klein［16］发表了基于该理论的SAS和R统计分析代码，通过案例研究证实该模型的拟合结果与累积风险模型的拟合效果相近。

3.联合分布函数为基础的分析方法

考虑到竞争风险型数据包含多结局事件及其对应的观测时间，前者构成结局事件的分布函数，后者构成观测时间的分布函数。Larson和Dinse［17］提出利用联合分布P（J，T）的来拟合目标结局事件P（J）的边际分布及其观测时间P（T｜J）的条件分布，即混合模型（mixturemodel）：

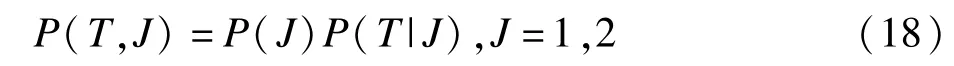
该联合分布函数要求随访已经结束，且需要利用EM（expectation-maximization）法修复删失观测，最后通过广义线性模型进行估计。鉴于混合模型理论过于复杂且要求研究已经完成，Nicolaie［18］提出使用观测时间分布P（T）和观察期内结局事件J的条件分布P（J｜T）拟合联合分布P（T，J），即纵向模型（vertical model）：

该理论定义结局事件J发生的条件概率P（J＝j｜T＝t）为相对原因别风险（relative cause-specific hazards，csRH），则在上述原因别风险模型的基础上csRH（t）可描述为：

值得注意的是，csRH与风险比（hzarad ratio，HR）是相同的，其也要求删失为非信息性删失，即：

式中，P（J＝j｜T＝t，C≥t）和P（J＝j｜T＝t，T≤t）分别表示t时刻受试者发生右删失和左删失的概率。若假设任意结局事件发生的时间为τt＝｛τ1，τ2，…，τT，根据公式（1）和公式（20）csRHj（τt）可以表达为：

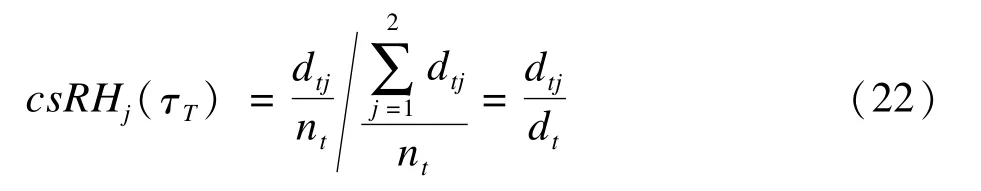
若假定csRHj（τt）为连续变量，则需要引入平滑函数B（τt）拟合每个时间点的csRHj（τt），此时通过多元logistic模型建立csRHj（τt）和B（τt）之间的关联，即为：

此外，在原因别风险模型的理论框架下，建立csRHj（τt）与结局事件j在t时间内累积发病率的关系如下：

式中，f′为全部结局事件发生时间的密度函数。此时，csRHj（t）可以描述为全部结局时间的分布密度函数在累积发病率函数中的比例。当存在协变量时，该模型可以进一步拓展，考虑到其拟合过程较为复杂，因此此处不再详述［18］。

竞争风险型数据统计分析研究进展及其应用

纵观竞争风险型数据统计分析发展史，我们不难发现竞争风险的本质是将删失事件进行更细致的归类和处理，其主要的理论分析框架仍为生存分析。然而，传统的生存分析，没有充分地认识到竞争事件对目标结局事件的影响或直接将竞争事件视为删失事件，导致结局事件的风险函数λ（t）出现有偏估计，继而引起生存函数S（t）和累积发病率函数F（t）出现有偏估计。现有竞争风险型数据分析方法，在考虑竞争事件的同时，直接研究干预因素对目标结局事件发生率的影响，改变了经典生存分析中将目标结局事件发生率的研究转换为发生风险研究的思路，更加直观、真实地评价干预对目标结局事件发生率的应用。但是，复杂的理论研究基础导致其缺少标准的统计分析软件包，进而阻碍了其在实际研究中的应用。值得庆幸的是，近年来国内越来越多的研究也开始关注竞争风险型数据的分析［19－20］。

［1］Lau B，Cole SR，Gange SJ．Competing risk regressionmodels for epidem iologic data．Am JEpidem iol，2009，170：244-256．

［2］Austin PC，Lee DS，Fine JP．Introduction to the Analysis of Survival Data in the Presence of Competing Risks．Circulation，2016，133：601-609．

［3］de Glas NA，Kiderlen M，Vandenbroucke JP，et al．Perform ing Survival Analyses in the Presence of Competing Risks：A Clinical Example in Older Breast Cancer Patients．JNatl Cancer Inst，2016：108．

［4］Suri RM，ClavelMA，Schaff HV，etal．Effectof RecurrentM itral Regurgitation Follow ing Degenerative M itral Valve Repair：Long－Term Analysis of Competing Outcomes．J Am Coll Cardiol，2016，67：488-498．

［5］Ryser MD，Worni M，Turner EL，et al．Outcomes of Active Surveillance for Ductal Carcinoma in Situ：A Computational Risk Analysis．J Natl Cancer Inst，2016：108．

［6］Chiang CL．Competing risks in mortality analysis．Annu Rev Public Health，1991，12：281-307．

［7］David CR．Regression models and life tables（w ith discussion）．Journal of the Royal Statistical Society，1972，34：187-220．

［8］Kaplan EL，Meier P．Nonparametric estimation from incomplete observations．Journal of the American statistical association，1958，53：457-481．

［9］Gray RJ．A class of K-sample tests for comparing the cumulative incidence of a competing risk．The Annals of statistics，1988：1141-1154．

［10］Prentice RL，Kalbfleisch JD，Peterson AV，Jr．，et al．The analysis of failure times in the presence of competing risks．Biometrics，1978，34：541-554．

［11］Sun Y，Hyun S，Gilbert P．Testing and estimation of time-varying cause-specific hazard ratios w ith covariate adjustment．Biometrics，2008，64：1070-1079．

［12］Fine JP，Gray RJ．A proportional hazardsmodel for the subdistribution of a competing risk．Journal of the American statistical association，1999，94：496-509．

［13］Klein JP．Modelling competing risks in cancer studies．Stat Med，2006，25：1015-1034．

［14］Andersen PK，Abildstrom SZ，Rosthφj S．Competing risks as a multistatemodel．Statisticalmethods inmedical research，2002，11：203-215．

［15］Andersen PK，Klein JP，Rosthφj S．Generalised linearmodels for correlated pseudo-observations，with applications to multi-state models．Biometrika，2003，90：15-27．

［16］Klein JP，Gerster M，Andersen PK，et al．SAS and R functions to compute pseudo-values for censored data regression．Comput Methods Programs Biomed，2008，89：289-300．

［17］Larson MG，Dinse GE．A mixturemodel for the regression analysisof competing risks data．Applied statistics，1985：201-211．

［18］Nicolaie MA，van Houwelingen HC，Putter H．Vertical modeling：a pattern mixture approach for competing risks modeling．Stat Med，2010，29：1190-1205．

［19］江一涛，胡海兰，魏巧玲，等．竞争风险模型的发展与应用．中国卫生统计，2009，26：445-447．

［20］肖媛媛，许传志，赵耐青．常用生存分析模型及其对时依性协变量效应的估计方法．中国卫生统计，2016：543-547+552．

（责任编辑：刘 壮）

△通信作者：范金虎，E-mail：fanjh＠cicams.ac.cn