随机误差对线性回归相关系数的影响

南京医科大学康达学院理学部数学与计算机教研室（222000） 丁 勇

·学术讨论·

随机误差对线性回归相关系数的影响

南京医科大学康达学院理学部数学与计算机教研室（222000） 丁 勇△

相关系数是统计分析的一个重要指标。由于研究对象的不同，相关系数的定义也不同。最常用的相关系数为简单相关系数或Pearson积差相关系数［1－3］。在实际问题中，如果两个变量存在线性关系，但由于观察或测量数据不可避免带有误差，这些误差必然对相关系数的计算产生一定的干扰，这些干扰会受到什么因素的影响，本文对此进行探讨。

方 法

1．相关系数公式

显然，如果没有随机误差，则x、y的相关系数的绝对值为1；当观察或测量数据有随机误差时，相关系数将发生变化。记x、y*的相关系数为r，则有［1－3］

根据公式（5）可得到｜r1｜与lεε、b2和lxx的关系图（图1），理论分析得到的结果与图是一致的。

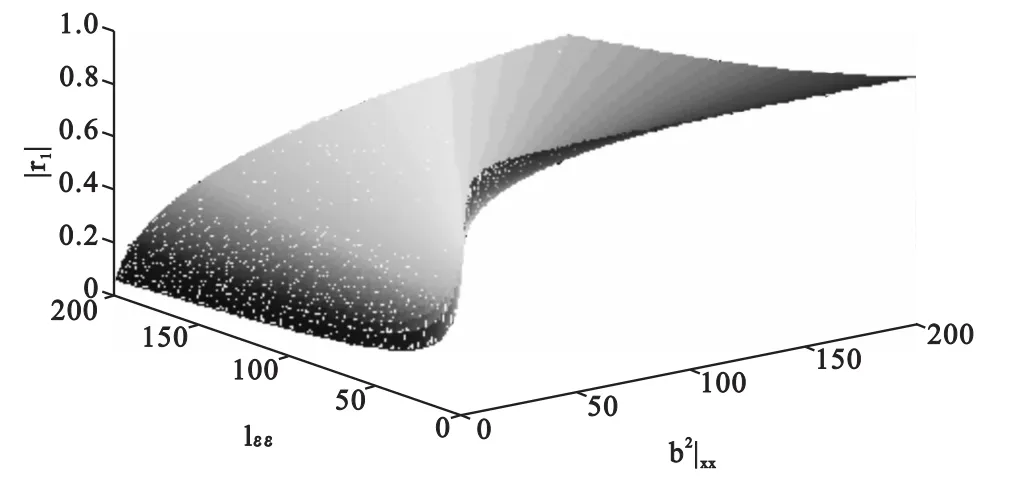
图1 ｜r1｜与b2lxx、lεε关系图

在实际应用中，样本量n一般不会很大，此时，｜r1｜上述这些性质是否对r成立？下面进行讨论。

由（1）式可知，r大小与直线的截距a无关，这与r1的性质是相同的。

由于b为直线的斜率，故当b＞0时，y随x的增大而增大，即y与x是正相关，当b＜0时，y随x的增大而减少，即y与x是负相关，所以r的符号应该与b相同。但由于误差的影响，由公式（1）可知，r的符号可能与b不相同，下面讨论发生这种情况的概率。

由于εi～N（0，σ2），且εi相互独立，所以lxε的方差为

计算机模拟

自蒙特卡罗方法于20世纪40年代作为一种独立的统计模拟方法被提出以来，已在多个研究领域得到了广泛的应用［5－6］。下面通过计算机模拟，对公式（6）～（9）进行验证。

先随机抽取［0．5，10］区间内均匀分布的18个数据，包括端点共20个数据作为x：0．5000 1．07401．4131 3．4909 4．0350 4．2566 4．4100 4．51215．1895 5．2536 5．3097 5．3989 5．4168 5．8319 6．7223 6．8272 7．3483 7．5297 8．1950 10．0000；这批数据的lxx＝107．1562。

再设直线方程为y＝2+bx，并分别考虑b＝± 0．1，±0．5，±1，±3，±5和σ＝1，2，3，5的各种情况。

每次模拟用计算机产生20个服从N（0，σ2）分布的随机数εi作为随机误差，再取yi＝2+bxi+εi（i＝1，2，…，20）。

每种情况共进行10000次模拟，统计结果见表1，其中p1表示b和r同号的概率，根据公式（6）或（7）计算；p2表示的概率，根据公式（8）或（9）计算；f1和f2分别表示10000次模拟中，b和r同号的频率和的频率。由于b＝－0．1，－0．5，－1，－3，－5结果与b＝0．1，0．5，1，3，5的结果几乎相同，故从略。

由表1可知，当b较大或误差较小时，b和r同号的概率很大。

表1 b和r同号和的概率、频率统计表（10000次模拟，lxx＝107．1562）

表1 b和r同号和的概率、频率统计表（10000次模拟，lxx＝107．1562）

b σ＝1p1f1p2f2σ＝2p1f1p2f2 0．1 0．8497 0．8472 0．8262 0．8258 0．6976 0．70310．6928 0．6890 0．5 1 1 0．9892 0．9930 0．9952 0．9951 0．9601 0．9608 1 1 1 0．9959 0．9985 1 1 0．9892 0．9923 3 0．9977 0．9991 1 1 0．9970 0．9990 5 1 1 0．9979 0．9996 1 1 0．9976 0．9993 1 1bσ＝3p1f1p2f2σ＝5p1f1p2f2 0．1 0．6350 0．6291 0．6334 0．6402 0．5820 0．58590．5816 0．5757 0．5 0．9578 0．9579 0．9161 0．9148 0．8497 08502 0．8262 0．8262 1 0．9997 0．9991 0．9772 0．9815 0．9808 0．9822 0．9392 0．9375 3 1 1 0．9959 0．9981 1 1 0．9920 0．9953 5 1 1 0．9972 0．9988 1 1 0．9959 0．9988

讨 论

在实际问题应用中，如果计算得到两个变量之间相关性不大，可能的原因是两者之间真的相关性不大；根据本文分析，也可能是测量的随机误差所造成，此时，提高测量精度和数据质量，可以提高相关性。

两个或多个变量的相关分析有着广泛的应用，相关系数是相关分析的一个重要指标，相关系数的大小直接影响统计推断的结论。因此，分析对相关系数的影响因素，具有重要的应用价值。本文推导了直线回归中有误差数据的相关系数公式（1）和大样本的较简单的近似公式（3），并分析了影响相关系数的因素。由（1）式和（4）式可知，相关系数的大小与直线的截距无关，这与我们的直观理解是一致的，截距的作用体现在散点图的数据点向上或向下平移的距离，不影响自变量和因变量的相关性。

公式（3）比较简单，通过理论分析即可得到相关系数绝对值与｜b｜、σ和lxx的关系，公式（1）相对复杂一些，我们用计算机模拟验证了理论分析结果的准确性。由本文的讨论可知，随机误差对相关系数的计算产生直接的干扰，随机误差越大，相关系数绝对值越小，｜b｜和x的离差平方和lxx在一定程度上对数据误差的干扰又有一定的影响，｜b｜和lxx越大，会减少随机误差的干扰。实际问题中，两变量之间存在线性关系是客观存在的，我们无法改变｜b｜，但通过本文的分析，我们知道较大的｜b｜对误差有一定的抗干扰作用；另一方面，在科研设计中，我们可以确定自变量的取值，通过加大自变量的离差来控制或减少误差的影响。

对误差性质进行分析，减少误差的影响，有助于提高研究问题的精确度和准确度［7］。本文是在x为非随机变量的情况下得到的结果，如果x为随机变量，问题的分析要复杂得多，但在实际应用中，往往将x作为非随机的情况来处理，对此做法有两点解释：一是可以把分析推断作为“条件化”的结论，二是如果（x，y）联合分布为正态，则x是否被看成随机的都无关紧要，有关研究可参看文献［8］。

［1］孙振球，徐勇勇．医学统计学．第4版．北京：人民卫生出版社，2014：314-351，131-154．

［2］徐维超．相关系数研究综述．广东工业大学学报，2012，29（3）：12-17．

［3］徐晓岭，王蓉华．概率论与数理统计．上海：上海交通大学出版社，2013：513-521．

［4］苏勇，熊斌．不等式的解题方法与技巧．上海：华东师范大学出版社，2012：30．

［5］李剑龙，陈方尧，李丹玲，等．具有相关关系的灵敏度和特异度的Monte Carlo模拟方法研究．中国卫生统计，2015，32（3）：417-420．

［6］刘成友，丁勇．相对误差直线回归模型两种参数估计方法的比较．中国卫生统计，2012，29（5）：1-3．

［7］丁勇．误差绝对值的统计特征和应用．数理统计与管理，2016：39-46

［8］陈希孺，王松桂．近代回归分析．合肥：安徽教育出版社，1987．

（责任编辑：邓 妍）

△通信作者：丁勇，E-mail：yding＠nimu．edu．cn