大质量中子星内部中微子辐射的相对论效应研究

丁文波,戚湛强

(渤海大学 数理学院，辽宁 锦州 121013)



大质量中子星内部中微子辐射的相对论效应研究

丁文波*,戚湛强

(渤海大学 数理学院，辽宁 锦州 121013)

通过相对论平均场理论和相关冷却理论，我们采用四组常用的核物质参数组(GL85, GM1,GPS250，GPS300)研究含有相对论效应和不含相对论效应两种情况下的大质量中子星冷却性质.结果表明，中微子辐射的相对论效应在大质量中子星(比如脉冲星PSR J1614 -2230)内部表现得较为显著.四组参数组中，GPS300参数组导致中微子发射率下降的幅度最大，而GM1参数组使得冷却速度降幅最明显.

中子星；相对论的中微子发射率；冷却

0 引言

中子星是宇宙中体积较小的一类星体，其半径约为10 km，但是它们的质量却能达到～2Msol(Msol表示太阳质量)，这些特性使其成为人们研究引力和致密物质性质的理想实验室〔1-2〕.在中子星诞生之初的106年里，冷却过程主要通过发射中微子来实现.在中微子主导的冷却过程中，效率最高的冷却过程当属核子的直接Urca过程(本文简称dUrca过程)〔3〕.

中子星的冷却速度主要由中微子发射率、中子星的结构和热导率决定.到目前为止，关于中微子发射率的表达形式主要有两种：一种是非相对论形式的，由Prakash和Lattimer于1991年首次给出〔4〕；另一种是相对论的表达式，由Leinson于2001年提出〔5〕.我们知道，dUrca过程发生的临界密度为～2n0(n0表示饱和核密度)，如此高的密度导致参与dUrca过程的粒子也都是相对论的，所以，为了保证所得数值结果更自洽，使用相对论公式去计算中微子发射率是十分必要的.

本文的主要目的是得出使用相对论和非相对论公式计算中微子发射率后，大质量中子星冷却性质的差异.在相对论平均场理论中，不同参数给出的中子星结构差异较大.为了得到较为全面的结果，本文的计算采用四组典型参数：GL85, GM1,GPS250和GPS300参数组.以前(尤其是2003年以前)关于中微子辐射的讨论多数都采用不含相对论效应的公式，若重新计算则工作量较大，因此，详尽地给出不同参数下、不同质量中子星的冷却性质在考虑相对论效应下的修正值将有助于前人科研成果的应用.

近年的观测数据显示中子星的质量可能比从前人们认为的还要大，尤其是2010年Demorest等人通过Shapiro延迟精确算得中子星PSR J1614-2230 的质量为(1.97±0.04)Msol〔6〕之后，关于大质量中子星的讨论便日趋热烈.本文主要研究大质量中子星内部中微子辐射的相对论效应，一方面是为了与观测数据相符，另一方面是因为相对论效应在大质量中子星内部较为显著.因此本文主要以1.60Msol和1.97Msol的中子星为研究对象(其中1.97Msol对应PSR J1614-2230)，争取尽可能全面地给出中微子辐射的相对论修正对其产生的影响.

1 理论模型和计算方法

本文我们采用相对论平均场理论(RMFT)的σ-ρ-ω标准模型〔7-8〕去描述中子星物质的特性〔9〕.拉格朗日密度L由三部分组成，分别是重子部分LB，介子部分Lm和轻子部分Ll.其中，重子部分包括质子p和中子n，轻子包括电子e和μ子.因此，体系的拉氏密度取以下形式(详见文献〔10〕)，

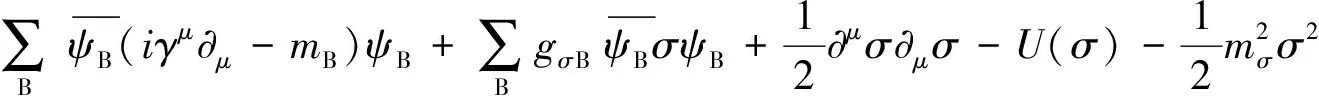
(1)

通过解欧拉-拉格朗日方程，获得三个介子场方程.解由场方程、化学平衡、重子数守恒、电中性条件等构成的非线性方程组〔11〕，可得中子星物质的性质，包括粒子化学势、数密度和体系EoS等，然后，将EoS作为输入量再通过求解TOV方程来获得中子星质量与半径之间的关系.

本文中，我们主要考虑最有效的冷却机制，核子的dUrca过程.核子的dUrca过程由两个连续反应组成，β衰变和轻子俘获，

(2)

相对论的中微子发射率为〔5〕

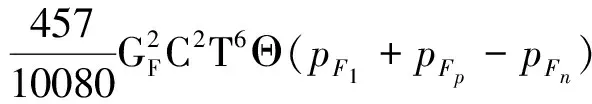
(3)

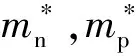
(4)

其中i代表核子，mi为核子裸质量,giσ表示核子和σ介子间的耦合常数.GF=1.436×10-49erg cm-3代表弱耦合常数，C=cosθc=0.973是Cabibbo因子.Cv=1和CA=1.26是矢量和同位旋矢量常量.非相对论的中微子发射率表达式(4)为

(5)

另外，阶跃函数Θ给出的是dUrca过程的发生条件，

pFl+pFp≥pFn

(6)

通过解冷却方程

(7)

可以获得其冷却曲线，其中，T和Cv分别表示中子星的内部温度和热容.Lv和Lγ代表中微子和光子的发光度.

中微子的发光度是通过中微子发射率按星体体积分计算得到的，而Lγ是光子的发光度，我们在这里采用经验公式

(8)

来进行近似计算，上式中Te,7=Te×10-7，而Te代表星体的表面有效温度，它与星体内部温度T的关系为

Te=10-2αT,0.1≤α≤1

(9)

2 讨论与结果

本文的计算中我们选择了最具代表性的传统中子星物质，粒子组分包括中子、质子、电子和μ子.所选用的四组参数组是：GL85、GM1、GPS250和GPS300.计算涉及的中子星主要为1.60Msol和1.97Msol的大质量星.

在图1中，我们展示了四组参数下，1.60Msol和1.97Msol质量中子星的中微子发射率在星体内部不同位置的变化曲线.总体来看，中微子发射率(相对论和非相对论)随着径向距离的增加而减小，且对于相同的径向距离，星体质量越大，中微子发射率越高(对照图1(a),(b)).这主要是因为1.97Msol质量中子星内部的密度高于1.60Msol中子星，使得中微子发射率的相关因子(见公式(3)和(5))在1.97Msol中子星明显偏高.而且对照图1(a),(b)可以发现质量越大的中子星dUrca过程发生的范围也越广.值得指出的是，考虑相对论效应后四组参数的中微子发射率普遍降低.对比图1(a)、(b)中四组参数的对应曲线，我们发现GPS250参数组的相对论的中微子发射率受到质量变化影响的幅度最大.而GPS300参数组则具有相对论和非相对论中微子发射率间的最大差距，这意味着GPS300是四组中对中微子发射率相对论效应最为敏感的参数组.

图1 四组参数下，1.60Msol(a)和1.97Msol(b)中子星由dUrca过程所导致的相对论(实线)和非相对论(虚线)的中微子发射率随半径的变化关系图

通过求解冷却方程，我们获得了不同质量中子星的冷却曲线，并呈现于图2中.图2看出，含相对论效应的冷却曲线(实线)高于对应的非相对论曲线(虚线)，这意味着相对论效应对中子星的冷却起抑制作用.为了更细致地研究相对论效应在各参数下对中子星冷却所产生的影响，我们对星体从初始温度冷却到4×108K的时间都做了统计，发现GM1数组所对应的中子星的冷却速度受相对论效应的抑制影响最为严重，在中子星取1.60Msol和1.97Msol时，非相对论对应的冷却时间为322年和352年，含相对论对应时冷却时间为502年和545年.GM1参数下中子星受相对论效应影响最严重，这一结论似乎与图1结论不一致，但事实上，除了中微子发射率外，热容和中微子发光度也是影响中子星冷却速率的复杂因素.对比图2(a)和(b)，可以发现与1.60Msol相比，1.97Msol中子星的冷却速度对参数的敏感度减弱，而对相对论效应的敏感度几乎不变.也就是说，对于中子星PSR J1614-2230，或者质量更大的中子星，其冷却性质的理论计算应考虑中微子辐射的相对论效应.

3 总结

本文对四组经典参数下的中子星在相对论和非相对论情况下的中微子发射率和冷却特性进行了研究.结果表明，中微子辐射的相对论效应在大质量中子星内部表现得较为显著，对于中子星PSRJ1614-2230或者质量更大的中子星，相对论效应不可忽略.相对论效应使中微子发射率和冷却速率均降低.在中微子发射率方面，对相对论效应最敏感的是GPS300参数组；而在冷却速率方面，受相对论效应影响最大的是GM1数组.

〔1〕KAMINKERAD,HAENSELP,YAKOVLEVDG.Nucleonsuperfluidityvsobservationsofcoolingneutronstars〔J〕.Astronomy&Astrophysics, 2001, 373(2):L17-L20.

〔2〕YAKOVLEV D G, LEVENFISH K P, POTEKHIN A Y, et al. Thermal states of coldest and hottest neutron stars in soft X-ray transients〔J〕. Astronomy & Astrophysics, 2004, 417(1): 169-179.

〔3〕COELHO E L, CHIAPPARINI M, BRACCO M E, et al. Neutrino emissivity, strong magnetic fields and cooling of neutron stars〔J〕. Astronomische Nachrichten, 2014, 335(6-7): 630-634.

〔4〕LATTIMER J M, PETHICK C J, PRAKASH M, et al. Direct URCA process in neutron stars〔J〕. Physical Review Letters, 1991, 66(21): 2701-2704.

〔5〕LEINSON L B, PEREZ A. Relativistic direct Urca processes in cooling neutron stars〔J〕. Physics Letters B, 2001, 518(1): 15-22.

〔6〕DEMOREST P B, PENNUCCI T, RANSOM S M, et al. A two-solar-mass neutron star measured using Shapiro delay〔J〕, Nature, 2010, 467(7319): 1081-1083.

〔7〕GLENDENNING N K. The hyperon composition of neutron stars〔J〕. Physics Letters B, 1982, 114(6): 392-396.

〔8〕GLENDENNING N K. Phase transitions and crystalline structures in neutron star cores〔J〕. Physics Reports, 2001, 342(6): 393-447.

〔9〕GLENDENNING N K, MOSZKOWSKI S A. Reconciliation of neutron-star masses and binding of the in hypernuclei〔J〕. Physical Review Letters, 1991, 67(18): 2414-2417.

〔10〕DING W B, LIU G Z, ZHU M F, et al. The influence of antikaon condensations on neutrino emissivity from neutron stars〔J〕. Astronomy & Astrophysics, 2009, 506(2): L13-L16.

〔11〕刘玉会，丁文波. 中子星中的超子相〔J〕, 渤海大学学报(自然科学版)， 2010, 31(3): 277-280．

Studies on relativistic effect on neutrino emission in neutron stars with large masses

DING Wen-bo，QI Zhan-qiang

(College of Mathematics and Physics, Bohai University, Jinzhou 121013, China)

In the relativistic mean field theory and cooling theories, we study cooling properties of neutron stars in both relativistic and non-relativistic ways in the four classical parameter sets, GL85, GM1, GPS250 and GPS300. The results indicate that relativistic effect on neutrino emission is obviously in massive neutron stars. GPS300 set leads to the biggest fall in neutrino emissivity between relativistic and non-relativistic cases in the four sets. Relativistic effect makes the neutron star cool more slowly, and we find that GM1 set leads to the largest disparity in cooling rate between relativistic and non-relativistic cases.

neutron star; relativistic neutrino emissivity; cooling

2016-03-15.

辽宁省教育厅一般项目(No:L2015005); 国家自然科学基金项目(No:11271055,No:11265009,No:11175077).

丁文波(1980-)，女，博士，副教授，主要从事理论物理方面的研究.

dingwenbo1980@163.com.

P145. 6

A

1673-0569(2016)04-0308-05