积分边值条件下一类发展包含的可解性

程 毅，康 悦，吴 睿

(1. 渤海大学 数理学院, 辽宁 锦州 121013; 2. 空军航空大学 基础部, 长春 130022 )



积分边值条件下一类发展包含的可解性

程 毅*,1，康 悦1，吴 睿2

(1. 渤海大学 数理学院, 辽宁 锦州 121013; 2. 空军航空大学 基础部, 长春 130022 )

本文讨论了一类发展包含y′(t)+By∈F(t,y)在积分边值条件下解的存在性问题，这里B为有界线性算子，F(t,y)是一个集值函数. 本文分别运用连续选择定理和Leray-Schauder定理证明了当F(t,y)在凸与非凸两种情况下解的存在性.

发展方程；集值函数；连续

0 引言和预备知识

近年来，关于积分边值条件下发展方程的可解性问题一直是国内外研究的热点内容之一，并且产生了许多优秀的研究成果〔1-4，7-10〕. 然而对于积分边值条件下发展包含的可解性问题,相关结果却很少. 因此，本文研究了在积分边值条件下一类发展包含y′(t)+By∈F(t,y)的可解性问题，其中B为有界线性算子，F(t,y)是一个集值函数. 下面介绍本文中需要的符号及基本概念.

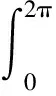
记

这里y′表示y的导数.C2π,V1,2(L,RN)是Banach空间，其范数分别为

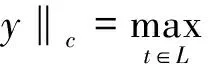
设[L,∑]是可度量的Lebesgue空间，Y是可分的Banach空间.

令M⊂Y的闭集,y∈Y,则y到集合M的距离定义为

d(y,M)=inf{|y-m|:m∈M}.

定义 Pf(Y)={M⊂Y:非空闭集}，令F:L→Pf(Y)是一个集值函数. 对于任意的z∈Y,当且仅当t→d(z,F(t))=inf{‖z-y‖:y∈F(t)}是可测的，F是可测的. 对于集值函数G:L→2Y{φ}，如果GrG={t,y}:y∈(t)}∈∑×N(Y),这里N(Y)是Y的Borel σ-域，则称函数G:L→2Y{φ}的图像是可测的. 对于∀M,N∈Pf(Y).(Pf(Y),h) 是完备的度量空间. 在Pf(Y)上定义广义度量为“Hausdorff度量”，记作

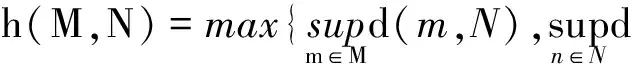
令X,Z是Hausdorff拓扑空间，G:X→2Z{φ}.G(·)为上半连续，若对于任意的C⊆Z是闭的且是非空的，那么G-(C)={x∈X:G(x)∩C≠φ}(G+(C)={x∈X:G(x)⊆C}在X内是闭的.

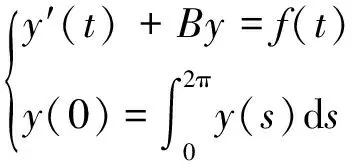
证明:首先考虑下面的柯西问题：

(1)

其中λ∈RN. 易知，问题(1)有唯一解，可表示为

(2)

对(2)两边同时取积分得

(3)

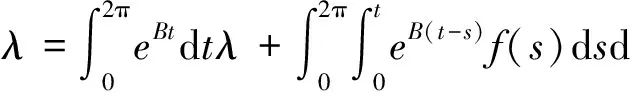
(4)

存在. 故将(4)代入(2)可得唯一解为

(5)

在(5)两边同时取范数得

其中M1,M2为某一常数. 故存在一个常数C>0使得‖y‖2≤C‖f‖2，即证明完毕.

1 主要研究结果

考虑下面微分包含问题：

(6)

这里B是从RN→RN的有界线性算子，F:L×RN→2RN是一个集值函数.

定义 1.1如果函数y∈V1,2(L,RN)，对于∀w∈RN和几乎所有的t∈L,并且存在函数f(t)∈F(t,y(t))满足：〈y′(t),w〉+〈By,w〉=〈f(t),w〉，则称y是问题(6)的解.

接下来证明当F是非凸值函数时问题(6)解的存在性. 需要如下假设：

G1:F:L×RN→RN是一个集值函数且是紧值的，并满足：

(i)(t,y)→F(t,y)是图像可测的；

(ii)对于几乎所有的t∈L,y→F(t,y)是下半连续的；

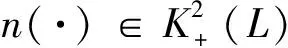
定理1.1 假设G1成立，则问题(6)存在解y∈V1,2(L,RN).

证明：对于∀y∈V1,2(L,RN)，记Ky=y′+By，则K:V1,2(L,RN)→K2(L,RN)是一个线性算子. 通过引理1.1，解的先验估计以及V1,2(L,RN)→K2(L,RN)是紧嵌入， 得到K:V1,2(L,RN)→K2(L,RN)是一一映射，又K是线性连续算子，因此我们有K-1:K2(L,RN)→V1,2(L,RN)是一个连续算子. 由于V1,2(L,RN)是紧嵌入K2(L,RN)，故K-1:K2(L,RN)→K2(L,RN)是全连续的.

接下来，设Q:K2(L,RN)→2K2(L,RN)是一个多值Nemitsky算子. 其定义为Q(y)={w∈K2(L,RN):w(t)∈F(t,y(t))}. 由文献〔5〕定理3.1得，Q(·)是可分解非空闭集，且下半连续.

根据文献〔6〕中连续选择定理，对于集值函数F存在一个连续映射f:K2(L,RN)→K2(L,RN),使得f(y)∈F(t,y). 故可以将原问题转化为如下不动点问题：y=K-1° f(y).我们利用Leray-Schauder替换定理证明这个不动点问题. 等价于考察集合W={y∈K2(L,RN):y=σK-1f(y),σ∈(0.1)}是有界集. 令y∈W，于是y=σK-1° f(y). 通过假设G1(iii)，得到

|f(y)|≤n(t)+c1|y|β.

即

由引理1.1，则存在常数c2>0，使得

‖y‖2≤c2‖f‖2.

故，我们有

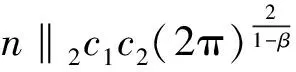
(7)

由于0<β<1，则一定存在一个常数M>0，使得‖y‖2≤M.假设不存在，由(7)，得到

(8)

当‖y‖2充分大时，(8)的右端小于1，故假设不成立. 因此W在K2(L,RN)内是有界集. 由于B是有界线性算子，从而存在一个常数c3>0，使得‖y‖1,2≤c3.根据Leray-Schauder替换定理，存在y∈V1,2(L,RN)，使y=K-1° f(y).，即y是问题(6)的解.

G2:F:L×RN→RN是集值函数且是紧凸值的，并满足：

(i)(t,y)→F(t,y)是图像可测的；

(ii)对于几乎所有的t∈L,y→F(t,y)是闭图像的；

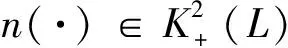
定理1.2 如果假设G2成立，那么问题(6)存在解y∈V1,2(L,RN),而且解集在V1,2(L,RN)中是弱紧的.

证明：根据定理2.1，K-1:K2(L,RN)→K2(L,RN)全连续，多值Nemitsky算子Q:K2(L,RN)→2K2(L,RN)是非空闭凸的.

下面证明Q(·)从V1,2(L,RN)到K2(L,RN)w是上半连续的. 设Qα是K2(L,RN)的非空弱闭子集,则等价于证明集合Q-1(Qα)={y∈E(K):Q(y)∩Qα≠φ}是闭的. 假设在V1,2(L,RN)中,存在函数列{yn}n≥1⊆Q-1(Qα)，使得yn→y. 故存在收敛子序列，不防设为本身yn(t)→y(t). 设fn∈Q(yn)∩Qα,n≥1. 由假设G2(iii)和Dunford-Pettis定理，则在K2(L,RN)中fn弱收敛f. 因此，又对于几乎所有的t∈L,得到

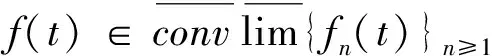
问题(6)等价如下不动点问题：

y∈K-1°Q(y).

由于K-1:K2(L,RN)→K2(L,RN)是全连续的，K-1°Q:K2(L,RN)→K2(L,RN)是上半连续的，且映有界集为相对紧集. 类似于定理2.1的证明

Γ1{y∈K-1(L,RN):y∈σK-1°Q(y),σ∈(0,1)}

是有界的. 根据集值Leray-Schauder替换定理，存在y∈V1,2(L,RN),使得y∈K-1°Q(y).显然，y是问题(6)的解.

令SP是问题(6)的解集. 类似定理2.1的证明得到解的先验估计. 故存在常数M>0,使|SP|=sup{‖u‖1,2:u∈SP}≤M. 由假设G2(iii)和Dunford-Pettis定理,假设在V1,2(L,RN)中yn→y. 故对几乎所有的t∈L，有

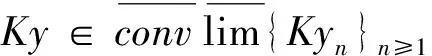
从而y∈SP,因此SP在V1,2(L,RN)中是弱紧集. 证毕.

2 结论

对于微分发展包含y′(t)+By∈F(t,y)在积分边值条件下解的存在性问题，本文证明了凸与非凸两种情况下解的存在性. 当F是集值函数且是紧值时，假设G1成立，主要利用连续选择定理和Leray-Schauder替换定理证明了微分包含(6)存在解y∈V1,2(L,RN)；当F是集值函数且是紧凸值时，假设G2成立，主要利用Dunford-Pettis定理证明了问题(6)存在解y∈V1,2(L,RN)且解集在V1,2(L,RN)中是弱紧的.

〔1〕HUA H, CONG F, CHENG Y. Notes on Existence and uniqueness of solutions for second order periodic-integrable boundary value problems〔J〕. Applied Mathematics Letters, 2012, 25(12): 2423-2428.

〔2〕LIU X L, SHI X Y. Existence of solutions for secondorder periodic-integrable boundary value problems〔J〕. Applied Mathematics Letters, 2014, 37(11): 91-94.

〔3〕XU Y S, MU J R, LIU X L. Numerical solution for secondorder periodic-integrable boundary value problems〔J〕. Far East Journal of Applied Mathematics, 2015, 92(2): 153.

〔4〕CABADA A, WANG G. Positive solutions of nonlinear fractional differential equations with integral boundary value conditions〔J〕. Journal of Mathematical Analysis and Applications, 2012, 389(1): 403-411.

〔5〕CHENG Y, CONG F, HUA H. Anti-periodic solutions for nonlinear evolution equations〔J〕. Advances in Difference Equations , 2012,165(12):1-12.

〔6〕DUGUNDJI J, GRANAS A. Fixed point theory monogr〔M〕. Springer Monographs in Mathematics, 2003.

〔7〕WANG Y, SHI Y. Eigenvalues of second-order difference equations with periodic and anti periodic boundary conditions〔J〕. Math. Anal. Appl,2005,309(12):56-69.

〔8〕ALSAEDI A, NTOUYAS S K, AGARWAL R P, et al. On Caputo-type sequential fractional differential equations with nonlocal integral boundary conditions〔J〕. Advances in Difference Equations, 2015, 2015(1): 1-12.

〔9〕AGARWAL R P, BALEANU D, HEDAYATI V, et al. Two fractional derivative inclusion problems via integral boundary condition〔J〕. Applied Mathematics and Computation, 2015, 257(4): 205-212.

〔10〕AHMAD B, NTOUYAS S K. Existence results for a coupled system of caputo type sequential fractional differential equations with nonlocal integral boundary conditions〔J〕. Applied Mathematics and Computation, 2015, 266(12): 615-622.

Solvability for integral boundary value conditions of a class of evolution inclusions

CHENG Yi1, KANG Yue1, WU Rui2

(1. College of Mathematics and Physics, Bohai University, Jinzhou 121013, China; 2. Department of Foundation, Aviation University of Air Force, Changchun 130022, China)

This paper discusses the existence of solutions of evolution inclusionsy′(t)+B(y) ∈F(t,y), whereBis a bounded linear operater andF(t) is a multifunction under integral boundary value conditions. We apply continuous selection theorem and Leray-Schauder′s theorem respectively to prove the existence of solutions for the convex cases and nonconvex cases onF(t,y).

evolution equation; multifunction; continuous

2016-08-28.

国家自然科学基金项目(No:11401042, 11301541).

程毅(1981-),男,博士，副教授,主要从事微分动力系统方面的研究.

chengyi407@126.com.

O175. 14

A

1673-0569(2016)04-0299-05