活泼灵动 感悟智慧

谢立光

在全国第九届“卡西欧杯”初中青年教师数学优质课展示与研讨活动中，江西省赣州市章源中学许萍老师执教了一节数学活动展示课——“从月历到数阵初步”，获得了在场评委及观摩教师的一致好评，被组委会评定为全国一等奖。许老师从“有框”到“无框”，从月历到数阵初步，设计了一系列数学活动，通过学生动手操作、观察、猜想、交流、反思、验证、运用数学规律，启发、引导学生从数学的角度发现和提出问题，运用已有的知识和经验解决问题。整节课活泼灵动，引领学生从活动经验中感悟数学智慧，彰显了数学活动课的魅力。现撷取部分教学片段与大家共赏。

【片段1】创设情境，引入课题

师：今天，我们从大家熟悉的月历中，开展一次数学活动。首先，我们一起来做一个“你说我猜”游戏。

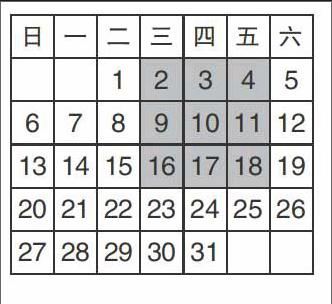
活动1：请你用一个学具“十字框”在2015年10月的月历表中框出5个数，然后告诉老师这5个数的和，让老师猜猜你框出的是哪5个数。

生1：我用“十字框”框出的5个数之和为100。

师： 见证奇迹的时刻到了，框出的中间的数是20，20的左、右、上、下对应的数分别是19，21，13，27。

生（齐声）：啊！老师猜对了。

生2：生1可能是老师的“托”，我来试一试。 我框出的5个数之和为60。

师：框出的中间的数是12，12的左右上下对应的数分别是11，13，5，19。

生：老师真厉害！

师：同学们想知道其中的奥秘吗？让我们一起来揭示其中的数学奥秘。

【赏析】许老师从学生熟悉的月历入手，游戏激趣，开展了“你说我猜”的数学游戏活动，设置了悬念，创设了一个宽松活泼的活动氛围，学生踊跃参与其中，有效地激发了学生参与活动的浓厚兴趣与探究数学问题的强烈动机。同时，让学生再一次深切地感受到“数学植根于生活，生活中处处有数学”。

【片段2】互动合作，探究规律

活动2：如图是2015年10月的月历。

（1）请你在该月历中用1×3（行×列）的“横条框”框出三个数，这三个数有什么规律？它们的和与中间这个数有什么关系？移动方框再试一试。

（2）再用3×1（行×列）的“竖条框”框出三个数，你能得出什么结论？

（3）设其中一个数为a，你能证明（1）、（2）中的结论吗？

（学生纷纷利用学具“条形框”框数，观察思考，寻找规律；计算所框3个数的和与中间这个数的数量关系；利用含a的式子验证规律。而后小组交流学习活动成果，学生展示探究过程与结论。）

活动小组1：我们的“横条框”所框1×3（行×列）的数是：5，6，7。发现这3个数从左到右依次大1，它们是一组连续正整数，它们的和是中间这个数的3倍。移动方框后，发现规律也是一样的，也就是“同行3个数从左到右依次大1” “同行3个数的和是中间这个数的3倍”。

活动小组2：我们的“竖条框”所框3×1（行×列）的数是：9，16，23。发现这3个数从上到下依次大7，我们认为其中的原因是由于月历中“一个星期有7天”周期性排列造成的。它们的和是中间这个数的3倍。移动方框后，发现规律也是一样的。也就是“同列3个数从上到下依次大7” “同列3个数的和是中间这个数的3倍”。

师：同学们真棒！观察仔细，思考严密，对规律归纳得很好！

活动小组3：证明“同列3个数的和是中间这个数的3倍”的思路也有3种，其中最简便的是：设中间的数为a，可得（a-7）+ a +（a+7）=3a。

师：同学们利用字母代表数，运用整式的有关知识，对结论进行了证明，思路清晰，方法多样，老师为你们点赞！

【赏析】学生兴趣盎然地利用学具“横条框”“竖条框”，分别对月历中的1×3（行×列）、3×1（行×列）中的3个数蕴含的数字规律、数量关系，进行动手操作、观察实验、分析归纳、概括总结、推理论证，积累了数学活动经验，体会了“用字母代表数更具一般性”的事实，体验了解决问题方法的个性化、多样化、简单化，同时增强了学生用语言、符号表示数学规律的意识与能力。

活动3：如图，在2015年9月的月历中用3×3（行×列）的“方形框”框出9个数，请思考下列问题：

（1）方框中这9个数的和与方框正中心的数有什么关系？

（2）移动方框，（1）中的结论还成立吗？你能证明这个结论吗？

（3）这个结论对任何一个月的月历都成立吗？

（根据活动2的经验，问题得到快速的解决，学生跃跃欲试，纷纷展示自己的探究活动成果。）

生1：我发现方框中这9个数的和是方框正中心数的9倍。移动方框，只要框中是9个数，结论仍然成立。

生2：可设方框正中心数为a，则（a-8）+（a-7）+（a-6）+（a-1）+a+（a+1）+（a+6）+（a+7）+（a+8）=9a。通过证明，说明该结论是正确的。

生3：这个结论对任何一个月的月历都成立，因为每个月的月历的数字排列规律是一样的。

师：说得真好！我们通过“观察—猜想—验证”发现了不少月历中隐含的数学问题及规律。接下来，我们运用所发现的规律，来解决一些数学问题。

【赏析】从“条形框”到“方形框”探究月历中的数字规律，通过知识的正迁移进行相关的数学活动。启迪学生的数学智慧，鼓励学生从不同的角度发现规律，从数学的角度发现问题，提出问题，解决问题。学生运用所学的“整式”知识对发现的规律进行解释、验证，从特殊到一般，推广到每个月的月历均蕴含其中规律，体现了结论的一般性。

【片段3】拓展应用，能力提升

活动4：如图的10×5（行×列）的数阵，是由一些连续奇数组成的。

（1）请你选择手中的学具方框框出几个数，你发现有类似于月历中的规律吗？

（2）若用如图所示的“平行四边形框”框出四个数：

①若设框中的第一行第一个数为x，用含x的代数式表示另外三个数；

②若这样框出的四个数的和是200，求出这四个数；

③能否框出这样的四个数，它们的和为256，为什么？

（学生读题、审题，运用学具“横条框”“竖条框”“十字框”“方形框”框数，自主探究，合作交流，揭示连续奇数数阵隐含的规律，展示活动成果。）

生1：我用的是“横条框”，发现所框3个数从左到右依次大2，3个数的和是中间这个数的3倍。

生2：我用的是“竖条框”，发现所框3个数从上到下依次大10，3个数的和是中间这个数的3倍。

生3：我用的是“十字框”， 发现所框5个数的和是中间这个数的5倍。

生4：我用的是“方形框”， 发现所框9个数的和是中间这个数的9倍。

生5（补充）：上述规律与月历中的规律类似。

生6：设框中的第一行第一个数为x，“平行四边形框”框出的另外三个数可表示为：x+2，x+8，x+10。列方程可得：x+（x+2）+（x+8）+（x+10）=200，解得x=45，这4个数分别是：45，47，53，55。

师：不错，根据规律，列方程求解。

生7（解法同生6）：可得和为256的4个数分别是：59，61，67，69，能框出这4个数。

（学生们各抒己见，争论不休，而后恍然大悟。）

生：“平行四边形框”不能框出这样的4个数，因为59与61，67，69在数阵的两端。

师：看来，解得的结果要回归到数阵中去检验它的存在性。

【赏析】教学中，许老师从“月历”到“连续奇数数阵”，从“横条框”“竖条框”“十字框”“方形框”到“平行四边形框”，从简单到复杂，引导学生发现数阵的数字排列规律。由于有前面的数学活动经验的积累，学生能快速、敏锐地发现数阵隐含的数字规律，问题迎刃而解，学生进一步感受到运用数学活动经验解决数学问题带来的成功愉悦。学生动手操作，质疑反思，合作交流，展示汇报，将实际问题转化为数学模型求解，展示了学生的聪明才智、独特个性与创新成果，积累了活动经验，提炼了思想方法，使学生在活动中理解数学本质，感悟数学智慧。

（作者单位：江西省赣县教育局教研室）