浅谈中学数学恒成立问题的解决策略与方法
2017-01-09赵志鸿
赵志鸿●
江苏省南京市湖滨高级中学(210000)
浅谈中学数学恒成立问题的解决策略与方法
赵志鸿●
江苏省南京市湖滨高级中学(210000)
在中学数学学习过程中经常遇到“恒成立”的问题,由于解析该种问题具有很强的抽象性与逻辑思维性,因此“恒成立”问题就是学习数学的重点,也是难点.很多学生对该知识点的掌握不是很完善,为了帮助学生掌握“恒成立”问题的解决要点,首相要将“恒”字作为突破口,主要是考察学生转换以及知识的灵活运用程度,对于学生的综合能力的培养是非常有意义的.
一、函数最值法
在“恒成立”问题中,函数最值法是最常用也是基本的解题方法.
例如:已知函数f(x)=(x+1)lnx-x+1,若xf′(x)≤x2+ax+1恒成立,求a的取值范围.

由以上题目可以看出,函数最值法是解决恒成立问题的简单而有效的方法,但关键是对题目的恰当变形处理.
二、分离参数法
“恒成立”问题类型多样,在面对不同类型的问题时,解题方法也不同.例如,面对函数不等式类型的“恒成立”问题时应该采用分离参数法.和函数最值法类似在采用分离参数法时首先要将函数进行变形处理,经过变形处理的函数其参数被分离出来,当函数变成只含有一段的解析式,这样函数变得更加简单、明了.有助于快速解决“恒成立问题”
例如:已知2a-3b=1,证明ax+by=5这条直线恒过定点.在这道题中已知2a-3b=1,便可以得出a=1/2(3b+1),把其代入直线方程式后,分离参数b可以出(x-10)+b(3x+2y)=0.又由x-10=0与3x+2y=0得到x=10,y=-15.所以(x-10)+b(3x+2y)=0表示经过x-10=0与3x+2y=0这两条直线的交点(10,-15)的直线系方程.因此当2a-3b=1的时候,坐标(10,-15)是直线ax+by=5的恒过定点.该例题采用分离参数法来解决“恒成立”问题时,主要将含参数的项集中到一起,不含参数的项另集中到一起,再用恒等式的方法加以解决.
三、把不等式恒成立问题转化为函数图象问题
对于不等式恒成立问题,这类题目可能一开始束手无策,很难用初等数学的知识去解这个不等式,但如果想到数形结合的方法就可以很快解决.
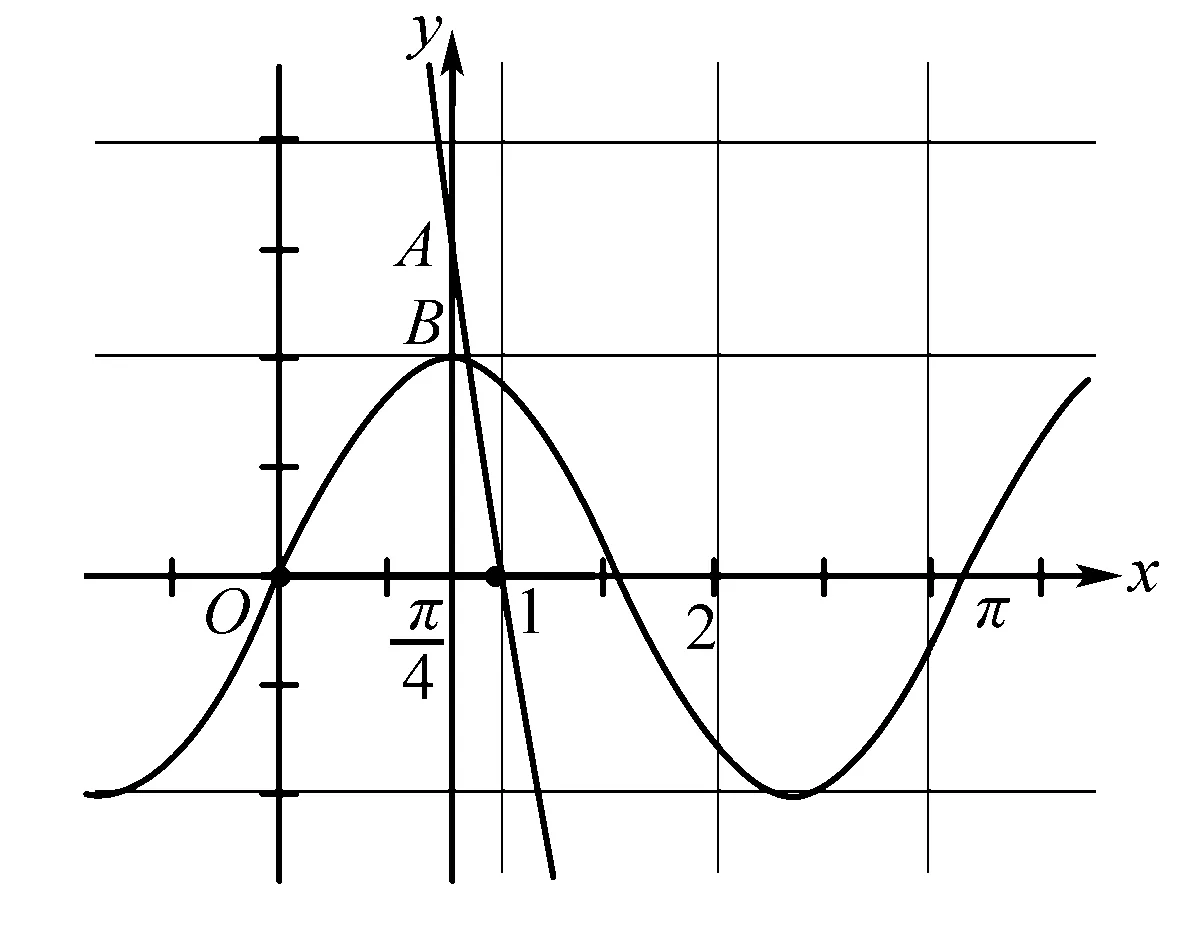
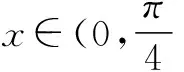
四、采用逆向思维,使用反证法
如果恒定问题,不能从正面解决,那么就从反面进行考虑,所以可以考虑反证法,会带来一些帮助解决的思绪.

解决恒成立问题的方法主要是将复杂的问题转化为一个简单易解决的问题.而要让学生做到正确的、灵活的转化,就要求我们在中学数学的教学过程中,经常引导学生对典型问题的典型解法加以研究并自觉地疏理知识,形成知识板块结构和方法体系,不断提高在数学学习过程中的解题问题的能力,提高信心.
G632
B
1008-0333(2016)34-0034-01
