三角函数最值问题的解题技巧

谭春林●

江苏省南京市秦淮中学(211100)

三角函数最值问题的解题技巧

谭春林●

江苏省南京市秦淮中学(211100)

三角函数最值问题一般涉足的范围比较广，因此对此类问题要力争做到吃透.本文将通过一些实例，对三角函数最值问题的解题技巧进行深入的研究.

1.利用三角函数的有界性

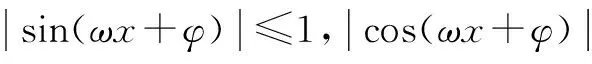
解析 先经过三角恒等变形，得

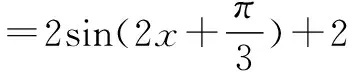
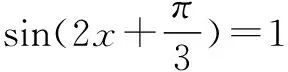
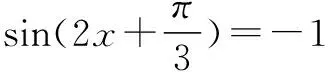
点拨 通过例题可知，利用三角函数的有界性，一般需要把三角函数式作适当的变形，化为含有某一个三角函数式以后，再根据性质来判断所给出三角函数的最值.

2.不等式法

所谓不等式法就是利用不等式求最值的知识进行解题.利用此方法，只需要我们能找出一个目标函数以及与题设条件都有关的不等式即可.但是需要我们特别注意的是在利用此方法求三角函数的最值时，使函数达到极值的自变量x必须在允许值的范围之内，否则就会发生错误，这时就要重新考虑运用其他方法进行解题.

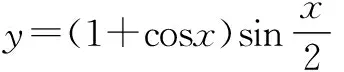
点拨 通过例题可以看出利用不等式法进行解题，即就是根据代数不等式a2+b2≥2ab(a>0,b>0)来解，但是在有些题目中仅仅运用此不等式是错误的，其原因在于当且仅当时未取等.此外除了应用一般不等式及定和、定积定理外，有时还需要结合函数的有界性、解二次不等式等知识进行解题.

3.换元法

换元法作为高中数学的最为经典的方法，其应用范围很广，其在解答三角函数的最值问题中也有很大的应用.换元法在三角函数的最值问题中的使用一般都是将三角函数的表达式中的函数进行整体代换，从而运用代数函数如二次函数等知识求最值.

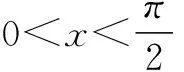
点拨 从例题中可看出，应用换元法解题，其在解题过程中依旧蕴含其他的解题方法，因此学生对其他的解题方法也要深入了解.此外需要特别注意的是，换元不仅将变量换掉，也要将其对应的定义域换掉，这往往是学生最容易忽视的，也是使用换元法解题的易错点.

综上所述，在平常的学习或做题中无论是遇到求比较简单三角函数式的最值，还是复杂的三角函数式，只要选择正确的解题方法和技巧，并在解题过程中多加细心，就一定能实现高效的解题.

G632

B

1008-0333(2016)34-0020-01