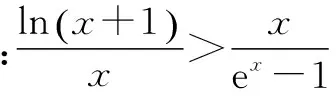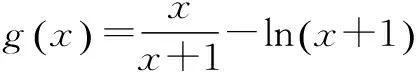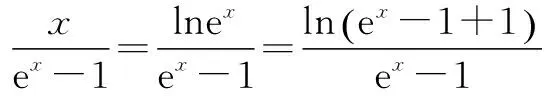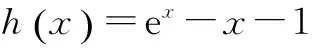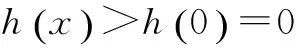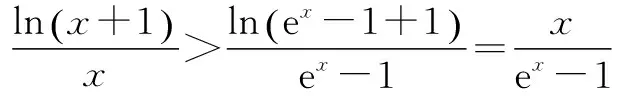一元函数不等式的证明方法
2017-01-09朱东海
朱东海●
云南省蒙自市蒙自一中新校区(661199)
一元函数不等式的证明方法
朱东海●
云南省蒙自市蒙自一中新校区(661199)
一元函数不等式的证明是高考中常考的问题,处理的方法一般有以下几种.
一、利用不等式两边之差构造函数
1.对于不等式两边的函数比较简单时,可直接做差构造函数
例1 (2015黑龙江省哈六中高三上学期期中考试数学文22题改编)已知函数f(x)=ex-x2+a,x∈R的图象在点x=0处的切线为y=bx.
(1)求函数f(x)的解析式;
(2)当x∈R时,求证f(x)≥-x2+x;
解 (1)∵f(x)=ex-x2+a,∴f′(x)=ex-2x

(2)设g(x)=f(x)+x2-x=ex-x-1,则g′(x)=ex-1. 令g′(x)>0得x>0,令g′(x)<0得x<0,所以g(x)在(-∞,0)上单调递减;在(0,+∞)上单调递增.从而g(x)min=g(0)=0,故f(x)≥-x2+x.
2.若不等式可以进行等价变换,则变形(代换、比商等)后再作差构造函数
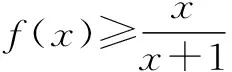
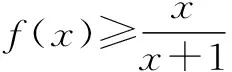
令g(x)=ex-x-1,则g′(x)=ex-1.
∴当x>0时,g(x)在区间(-1,0)上是增函数;
当x<0时,g(x)在区间(0,+∞)上是减函数.
因此当x=0时g(x)取得最小值,而g(0)=0,
故当x>-1时g(x)≥0,也就是ex≥x+1.
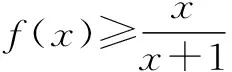
3.对“隐零点”处理
例1和例2中的导数的零点是可以求出的,对导函数的零点,根据其数值计算上的差异,我们可以分为两类:一类是数值上能精确求解的,我们不妨称为“显零点”;另一类是能判断其存在但数值上无法精确求解的,我们不妨称为“隐零点”;对“隐零点”处理的基本方法为“虚设及代换”.
例3 (2015届四川省德阳市高三第一次诊断考试数学理21题改编)已知函数f(x)=ax+lnx,函数g(x)=ex,其中e为自然对数的底数.
(1)讨论f(x)的单调性;
(2)当a=0时,对于∀x∈(0,+∞),求证:f(x) ①当a≥0时,f′(x)>0,∴f(x)在(0,+∞)上为增函数. 综上所述,当a≥0时,f(x)在(0,+∞)上为增函数. (2)当a=0时,f(x)=lnx,令φ(x)=g(x)-f(x)-2,则φ(x)=ex-lnx-2, ∵当x∈(0,t)时,φ′(x)<0,φ(x)在(0,t)上为减函数;当x∈(t,+∞)时,φ′(x)>0,φ(x)在(t,+∞)上为增函数, ∴φ(x)min=φ(t)=et-lnt-2=et-lne-t-2=et+t-2. ∴f(x) 对f(x)>g(x)型的不等式,若函数h(x)=f(x)-g(x)的最小值不易求出,则可考虑用f(x)min>g(x)max来证明f(x)>g(x)型的不等式,在证明之前,尽可能将不等式等价变形,使f(x)min和g(x)max容易求出. (1)若f(x)在(m,m+1)上存在极值,求实数m的取值范围; 因此当x∈(0,1)时,f′(x)>0,f(x)为增函数; 当x∈(1,+∞)时,f′(x)<0,f(x)为减函数; 所以x=1是f(x)的极大值点. 而f(x)在(m,m+1)上存在极值, ∴m<1 故实数m的取值范围是(0,1). ∵x>1,∴t′(x)>0,从而t(x)在(1,+∞)上是单调递增函数. ∴t(x)>t(1)=1>0,也就是g′(x)>0, 因此g(x)在(1,+∞)上是单调递增函数. ∵x>1,∴1-ex<0.因此h′(x)<0,即h(x)在(1,+∞)上是单调递减函数. 若不等式两边有相同“结构”,则利用其“结构”的特征构造函数. 故要证原不等式成立,只需证明:当x>0时,x G632 B 1008-0333(2016)34-0016-02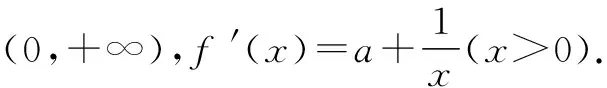
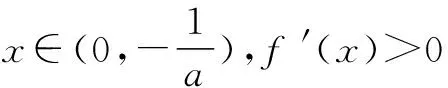




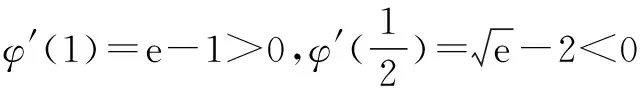
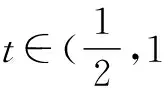
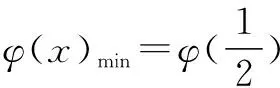
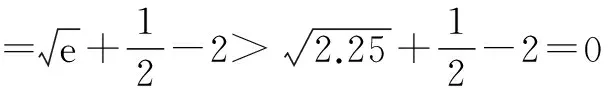
二、利用f(x)min>g(x)max来证明f(x)>g(x)型的不等式
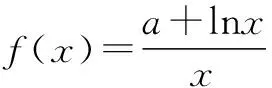
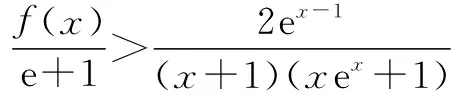

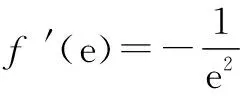
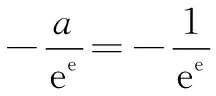
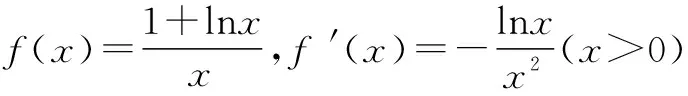



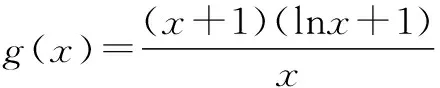

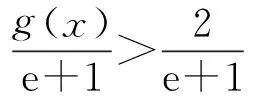
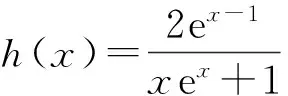

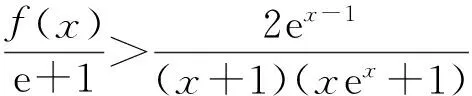
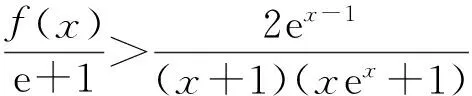
三、 利用不等式两边相同“结构”的特征构造辅助函数