高考函数命题的新动向——函数中的五点

张德文● 陈 亮●

湖南省浏阳市第一中学(410300)

高考函数命题的新动向
——函数中的五点

张德文● 陈 亮●

湖南省浏阳市第一中学(410300)

函数是贯穿中学数学的一条主线，是学好高等数学的基础，每年的高考对函数问题的考查所占的比例都很大，可以说是常考常新.其中涉及函数的零点、极值点、拐点、不动点、稳定点的问题，是高考命题的新动向；是考查函数知识的一个新“亮点”.下面举例说明，旨在总结这部分试题的考题类型，并揭示解决此类问题的方法与规律.

一、函数的零点

函数零点的定义：对于函数y=f(x)，把f(x)=0的实数x叫做函数y=f(x)的零点.函数零点的判定的常用方法有:(1)零点存在定理;(2)数形结合;(3)解方程f(x)=0.

例1 (2016年全国高考压轴题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.(Ⅰ)求a的取值范围；(Ⅱ)设x1，x2是f(x)的两个零点，证明：x1+x2<2.

解 (Ⅰ)f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).(ⅰ)设a=0,则f(x)=(x-2)ex,f(x)只有一个零点.

(ⅲ)设a<0,由f′(x)=0得x=1或x=ln(-2a).

综上，a的取值范围为(0,+∞).

(Ⅱ)不妨设x1f(2-x2),即f(2-x2)<0.

由于f(2-x2)=-x2e2-x2+a(x2-1)2,而f(x2)=(x2-2)ex2+a(x2-1)2=0,所以f(2-x2)=-x2e2-x2-(x2-2)ex2.设g(x)=-xe2-x-(x-2)ex,则g′(x)=(x-1)(e2-x-ex).所以当x>1时，g′(x)<0,而g(1)=0,故当x>1时，g(x)<0.从而g(x2)=f(2-x2)<0,故x1+x2<2.

二、函数的极值点

定义 设函数y=f(x)在点x0附近有定义，如果对x0附近的所有的点都有f(x)f(x0)则称f(x0)为y=f(x)的一个极小值，点(x0，f(x0))为y=f(x)的一个极小值点.极大值点和极小值点统称极值点.对于可导函数，若x0为极值点，则f′(x0)=0

例2 设x=1和x=2是函数f(x)=x5+ax3+bx+1的两个极值点.(Ⅰ)求a、b的值； (Ⅱ)求f(x)的单调区间.

解 (Ⅰ)f′(x)=5x4+3ax2+b,由假设知f′(1)=5+3a+b=0,f′(2)=24×5+22×3a+b=0.

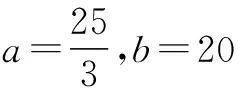
(Ⅱ)由(Ⅰ)知f′(x)=5x4-25x2+20=5(x2-1)(x2-4)=5(x+1)(x+2)(x-1)(x-2).

当x∈(-∞,-2)∪(-1,1)∪(2,+∞)时，f′(x)>0，当x∈(-2,-1)∪(1,2)时，f′(x)<0.

因此f(x)的单调增区间是(-∞,-2),(-1,1),(2,+∞),f(x)的单调减区间是(-2,-1),(1,2).

三、函数的拐点

对于函数y=f(x)，做如下定义：设f″(x)是函数y=f(x)的导数y=f′(x)的导数，若方程f″(x)=0有实数解x0，则称点(x0，f(x0))为函数y=f(x)的“拐点”.

例3 已知三次函数y=ax3+bx2+cx+d的图象过点(0，2)，在x=1处的切线方程为：y=10x-3，且f″(1)=12.请解答以下问题：

(1)求函数y=f(x)的解析式及“拐点”P的坐标；

(2)检验y=f(x)的图象是否关于“拐点”P对称；

(3)证明：①任何一个三次函数y=ax3+bx2+cx+d(a≠0)均存在拐点.②猜测：任何一个三次函数是否一定存在对称中心？若存在，请写出对称中心的坐标，不需证明；若不存在，请举一反例.

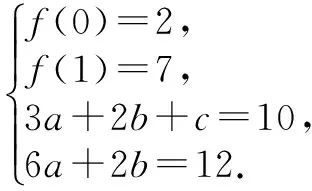
∴y=x3+3x2+x+2.再由f″(x0)=0得6x0+6=0，∴x0=-1.故P(-1，3).

(2)设A(x，y)为y=f(x)图象上一点，则A关于P对称点的坐标是(-2-x，6-y)，只需验证f(-2-x)+f(x)=6即可.由f(-2-x)+f(x)=(-2-x)3+3(-2-x)2+(-2-x)+2+x3+3x2+x+2=6，故y=f(x)图象关于P对称.

评注 本例实际上是把高等数学中的函数图象的“拐点”，用中学生能够理解的形式表述出来，这体现着在知识的接合点命题的思想.

四、函数的不动点

例4 (北京大学理科实验班入学考试题)f(x)的定义域是R，若c∈R使f(c)=c，则称c是f(x)的一个不动点.设f(x)的不动点数目是有限多个，下述命题是否正确？若正确，请给予证明；若不正确，请举一个例子说明.

▶▶ (1)f(x)是奇函数，则f(x)的不动点数目是奇数；(2)f(x)是偶函数，则f(x)的不动点数目是偶数.

解析 由新定义可知，函数f(x)的不动点个数就是函数y=f(x)与y=x的图象交点的个数.由于情境比较陌生，不妨先考虑两个特殊函数(如y=x3及y=1)的情形，显然y=x3与y=x的图象有三个交点，因而猜想(1)正确，进而考虑证明它正确；而y=1与y=x的图象仅有一个交点，故(2)不正确.

(1)正确.证明如下：∵f(x)为奇函数，且x∈R,∴f(-0)=-f(0)，即f(0)=0.因此0是f(x)的一个不动点.假设c≠0是f(x)的不动点，则由定义知f(c)=c.又因为f(x)是奇函数，所以f(-c)=-f(c)=-c,因此-c也是f(x)的不动点.显然c≠-c，这表明f(x)的非0不动点如果存在，则必成对.又根据题设知f(x)只有有限个不动点，因此f(x)的不动点数目为奇数.

(2)不正确.例如，f(x)=1是偶函数，设c是f(x)=1的不动点，则一方面f(c)=c，另一方面f(c)=1，由此得c=1.因此f(x)=1有且只有一个不动点.故命题不正确.

五、函数的稳定点

例5 对于函数f(x)，若f(x)=x，则称x是f(x)的“不动点”;若f(f(x))=x，则称x是f(x)的“稳定点”.函数f(x)的“不动点”和“稳定点”的集合分别记为A和B，即A={x|f(x)=x}，B={x|f(f(x))=x}.

(1)求证：A⊆B;(2)若f(x)=ax2-1(a∈R，x∈R)，且A=B≠Ø，求实数a的取值范围.

证明 (1)若A=Ø，则A⊆B，显然成立；

若A≠Ø，设t∈A，则f(t)=t，f(f(t))=f(t)=t,

即t∈B，从而A⊆B.

(2)A中元素是方程f(x)=x即ax2-1=x的实根.

B中元素是方程a(ax2-1)2-1=x，即a3x4-2a2x2-x+a-1=0的实根.

由A⊆B知，上述方程左边含有一个因式ax2-x-1，即方程可化为(ax2-x-1)(a2x2+ax-a+1)=0

因此要A=B，则方程a2x2+ax-a+1=0①要么没有实根，要么实根是方程ax2-x-1=0②的根.

若①没有实根，则Δ=a2-4a2(1-a)<0，由此解得a<3/4,若①有实根，则①的实根是②的实根，由②有a2x2=ax+a,代入①，有2ax+1=0，由此解得x=-1/2a.

故a的取值范围是[-1/4，3/4].

C.电容器的电容为kmgd/U2

D.将极板N向下缓慢移动一小段距离，油滴将向上运动

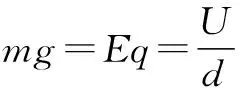
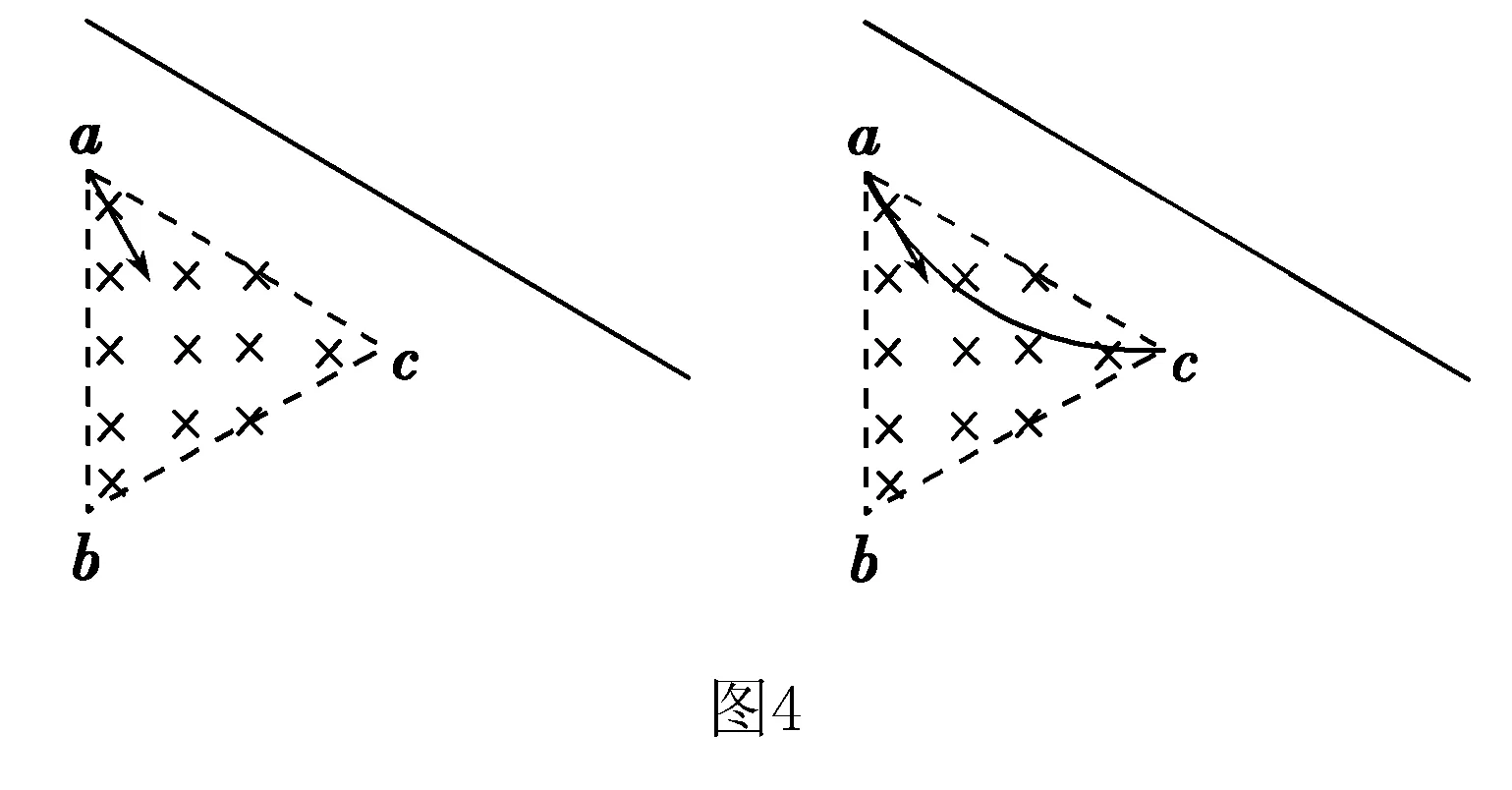
例4 如图4所示，正三角形abc区域内有匀强磁场，方向垂直于纸面向里，在斜上方有一与边ac平行的屏.正三角形边长为L，且ab边竖直.质量为m、电荷量为+q的粒子，以大小为v0的速度与ab边成30°角垂直射入磁场后从ac穿出，并以与屏成30°角方向打在屏上，不计粒子所受的重力.则关于磁场的磁感应强度的可能值为( ).

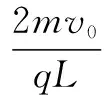
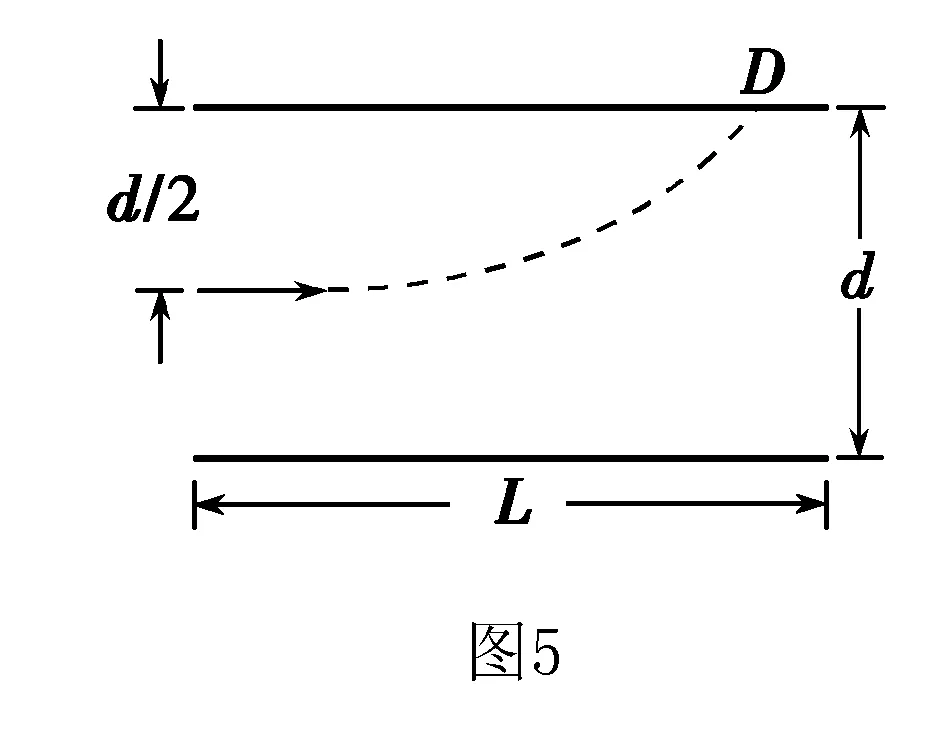
例5 有一平行板电容器，内部为真空，两个极板的间距为d，极板长为L，极板间有一匀强电场，U为两极板间的电压，电子从极板左端的正中央以初速度v0射入，其方向平行于极板，并打在极板上的D点，如图5所示.电子的电荷量用e表示，质量用m表示，重力不计.求：(1)电子打到D点时的动能；(2)D点与电子出发点间的水平距离；(3)电子的初速度必须满足什么条件，电子才能飞出极板.

解析 (1)设电子打到D点时的动能为Ek，

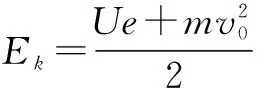
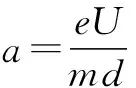
(3)设电子刚好能打到极板边缘时的入射初速度为v，L=vt， ⑥

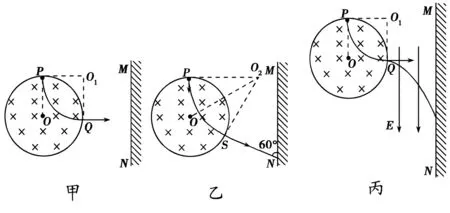
例6 如图6所示，在半径为R的圆形区域内有水平向里的匀强磁场，圆形区域右侧距离圆形区域右边缘距离为d处有一竖直感光板.圆形区域上侧有两块平行金属极板，金属极板上侧有一粒子源，粒子源中可以发射速度很小的质量为m的2价阳离子(带电荷量为+2e)，离子重力不计.(1)若离子从圆弧顶点P以速率v0平行于纸面进入磁场，求在两块平行金属极板间所加的电压U；(2)若离子从圆弧顶点P以速率v0对准圆心射入，若它刚好从圆形区域右侧射出，垂直打在竖直感光板上，求圆形区域内磁场的磁感应强度B；(3)若圆形区域内磁场的磁感应强度为B，离子以某一速度对准圆心射入，若它从圆形区域右侧射出，以与竖直感光板成60°角的速度打在竖直感光板上，求它打到感光板上时的速度v的大小；(4)若在圆形区域右侧加上竖直向下的匀强电场，电场强度为E，粒子从圆弧顶点P以速率v0对准圆心射入，运动一段时间后水平射出磁场，求离子打在MN上的位置距离圆形区域圆心O的竖直高度h.

G632

B

1008-0333(2016)34-0023-02