大跨管道悬索桥抗风特性试验研究
2017-01-09张光举曹平辉四川省铁路产业投资集团有限责任公司四川成都610041
王 凯,张光举,曹平辉(四川省铁路产业投资集团有限责任公司, 四川成都 610041)
大跨管道悬索桥抗风特性试验研究
王 凯,张光举,曹平辉
(四川省铁路产业投资集团有限责任公司, 四川成都 610041)
大跨度管道悬索桥,由于没有桥面板,其抗风特性与普通悬索桥具有一定的差异,目前没有专门的管道桥抗风规范,抗风问题已成为管道桥设计中的重要考虑因素。文章以某大跨度管道悬索桥为工程背景,总结山区峡谷管道桥设计风参数的选取方法,得到管道桥桥面高度处的设计风速。通过节段模型风洞试验,获取了管道桥的气动力系数,为桥梁的抗风设计提供重要参数。通过节段段模型动力试验,详细研究了该桥的气动性能。最后给出了管道桥的全桥气弹模型试验的风致响应特性。研究结果表明,跨度不超过300 m的管道悬索桥具有很好的抗风安全性,为以后管道桥抗风规范的编写等提供参考和依据。
管道桥;悬索桥;节段模型;气弹模型;风洞试验
在我们西南山区管道的修建过程中,经常需要跨越河流、湖泊、沼泽、冲沟、山谷等障碍物,这时就需要建设管道跨越结构[1]。当河谷的宽度比较大时,管道悬索桥就成为了跨越结构的首选桥型[2]。
大跨度悬索桥由于其结构轻柔、阻尼较小、自振频率低,对风的作用比较敏感,结构的抗风性能已成为大跨悬索桥设计中必须考虑的重要方面。颤振作为一种发散性的运动,在大跨桥梁抗风稳定性设计中是重点考虑的一环[3]。
由于管道悬索桥都是桁架结构,桁架梁是大跨度悬索桥较常采用的一种断面形式,桁架断面具有抗扭刚度大、透风率高及方便在运输困难地区施工等优点。但是桁架梁也有它特有的一些特性,如颤振性能较差等,因此对于管道悬索桥,有必要研究清楚大跨管道悬索桥可能出现的空气动力特性、大跨管道桥的风振等问题。
本文研究对象为西南山区一座主跨280 m钢桁梁管道悬索桥(图1),主梁为桁梁式结构,宽10 m,大缆采用双索面,垂跨比为1/10,桥面结构主要采用槽钢,由高强螺栓连接(图2)。桥塔采用钢箱式桥塔,每隔2 m设置一道横隔板,并设置检修通道。该桥处于深切峡谷地区,气象条件复杂。通过风参数计算、风洞试验等详细研究了大跨管道桥的抗风性能和抗风安全性。
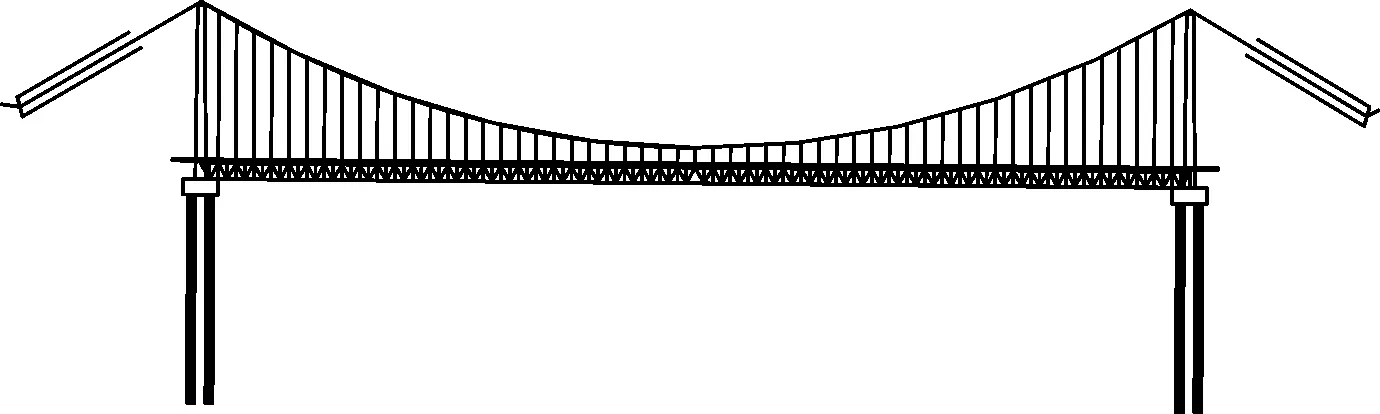
图1 桥型布置
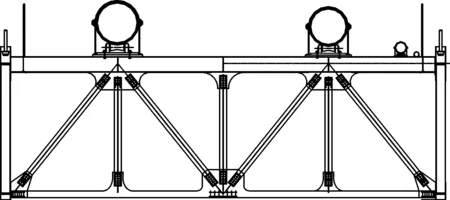
图2 主梁断面
1 桥位风参数
大桥桥址处为典型的峡谷地貌。为了准确把握桥址处的实际风环境,从《公路桥梁抗风设计规范》[4]中取得桥位200 km范围内三个地区的最大风速和对应的百年风速,应用统计学中Gumbel Type I 极值分布计算得到桥位处基本风速[5]为25.6 m/s。
由于大桥位于山区峡谷,桥面高度处设计基准风速的确定还需要考虑山区峡谷的影响,即山区峡谷对基本风速的修正。假设大桥桥址处“虚拟”标准气象站的基本风速为峡谷进口风速,对于建于峡谷处的桥梁,可以借用以下经验关系式获得设计基准风速[6]:
(1)
式中:ud为建于峡谷上口处桥梁的设计基准风速;u10为桥位虚拟气象站的基本风速,即设为峡谷进口风速;H为峡谷深度,当桥梁建于峡谷上口处,可取桥面至峡谷下底面的高度;B1为峡谷上口处宽度,一般为桥梁桥面长度;B2为峡谷下底面宽度;κ为山谷效应修正系数。由式(1)计算出大桥设计基准风速见表1。
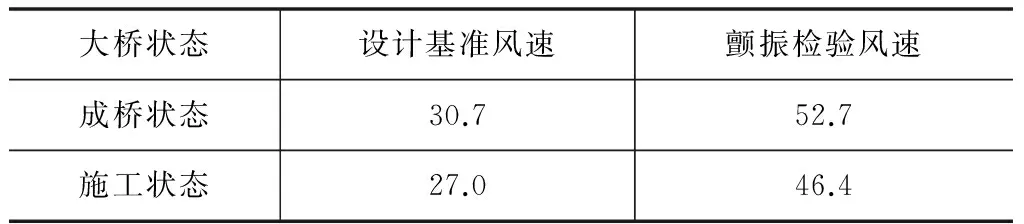
表1 设计风参数 m/s
2 有限元计算分析
根据前面的设计资料,采用通用的有限元软件对桥梁结构的动力特性进行计算分析,当有荷载作用在桥梁结构上时,桥梁结构会发生一定的几何变形,因此在进行模态分析前必须对结构进行恒载作用下静力分析,然后更新结构的几何刚度矩阵。在有限元计算中,大桥在成桥状态时,其约束条件为:桥塔底部按照实际条件设置固定约束,6个自由度全部限定;两个主塔处的墩柱在竖向、横向及顺桥向的扭转3个自由度与主梁进行耦合限定;主缆于锚碇处固定。计算出的桥梁结构成桥态下的振动频率和振动质量见表2。桥梁成桥态时的部分振型见图3。

表2 成桥状态结构动力特性
注:表格中—表示数值较大,即在该方向没有振动;振动特点中V表示竖向,L表示横向,T表示扭转,A表示正对称,S表示反对称,数字表示阶次。
3 节段模型试验
在进行阶段模型设计时,按照主梁的设计方案,主梁每个节间长1.25 m,考虑到制作模型时,模型的桁架节间为整数,模型采用1∶19.5的几何缩尺比。模型弦杆采用优质木材制作,其余杆件、桥面防撞护栏、人行道护栏、检修轨道等均采用塑料板雕刻而成[7]。
3.1 静力试验
静力试验主要是测量主梁的静力三分力系数。静力三分力系数反映了风对桥梁结构的定常气动作用,是表征在平均风作用下各类结构断面受力情况的无量纲系数。通过测试主梁在不同攻角下的三分力系数,可以为主梁的静风稳定性计算、抖振计算等提供必要的计算参数,从而可评价主梁发生静风失稳的可能性和抖振力的大小。

(a) 第2阶振型(对称横弯0.25 Hz)
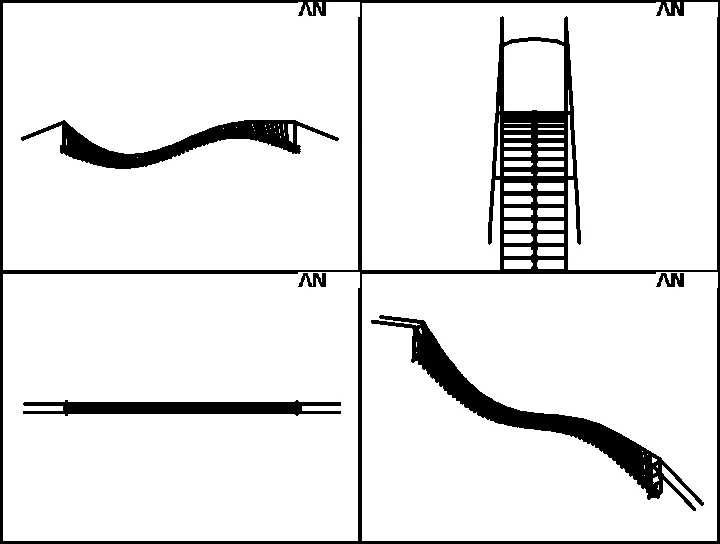
(b) 第3阶振型(反对称竖弯0.36 Hz)
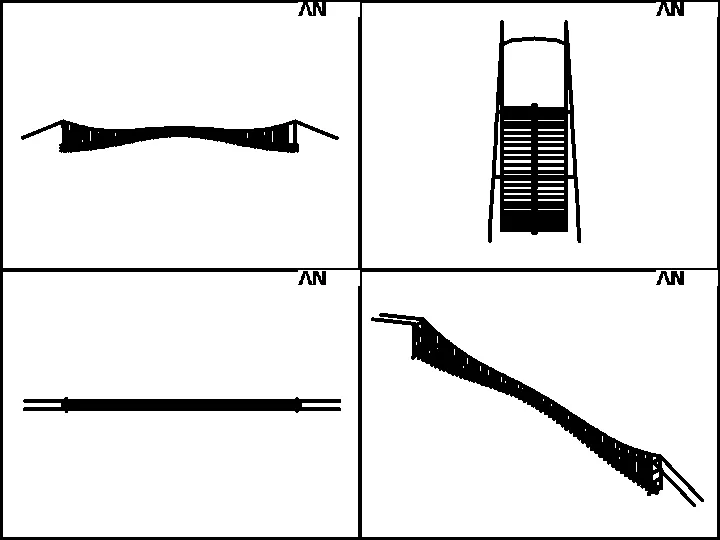
(c) 第4阶振型(对称竖弯0.43 Hz)
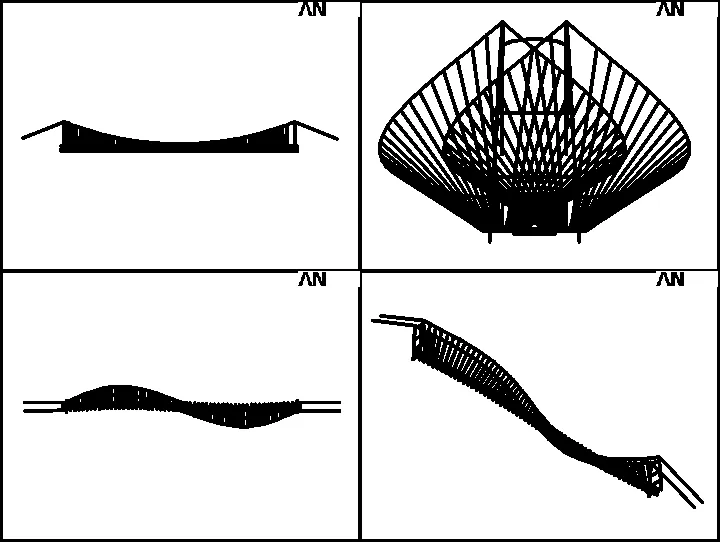
(d) 第8阶振型(反对称横弯0.89 Hz)图3 部分振型
试验在均匀流条件下进行,试验攻角为:α=-12°~+12°,Δα=1°。对管道悬索桥主跨标准梁段在成桥状态时进行试验,测试整体主梁在不同攻角下的三分力系数,测试风速15 m/s,试验结果分别以体轴和风轴系下的静力三分力系数曲线及数据列表的形式给出。静力试验的模型见图4,试验结果见图5。
3.2 动力试验
动力节段模型是用弹簧(模拟桥梁的等效刚度和弹性约束)将刚性节段模型悬挂在风洞中,通过直接测量随风速和攻角变化的振动信息,评价主梁的颤振和涡振性能的常用试验方法[8-9]。试验模型采用和静力试验相同的模型,表3为动力试验模型的参数。图6为安装在风洞中的动力试验模型。

图4 静力试验的节段模型
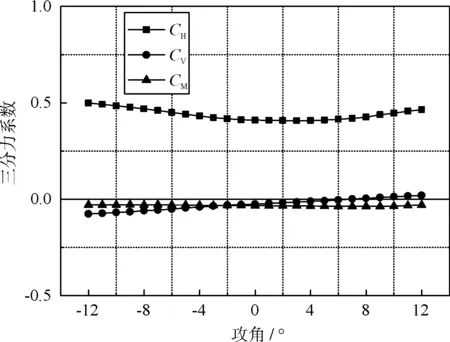
(a) 体轴系
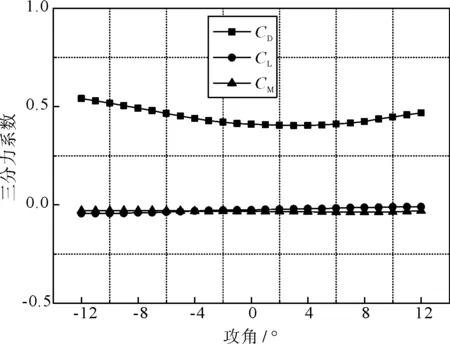
(b) 风轴系图5 主梁三分力系数曲线
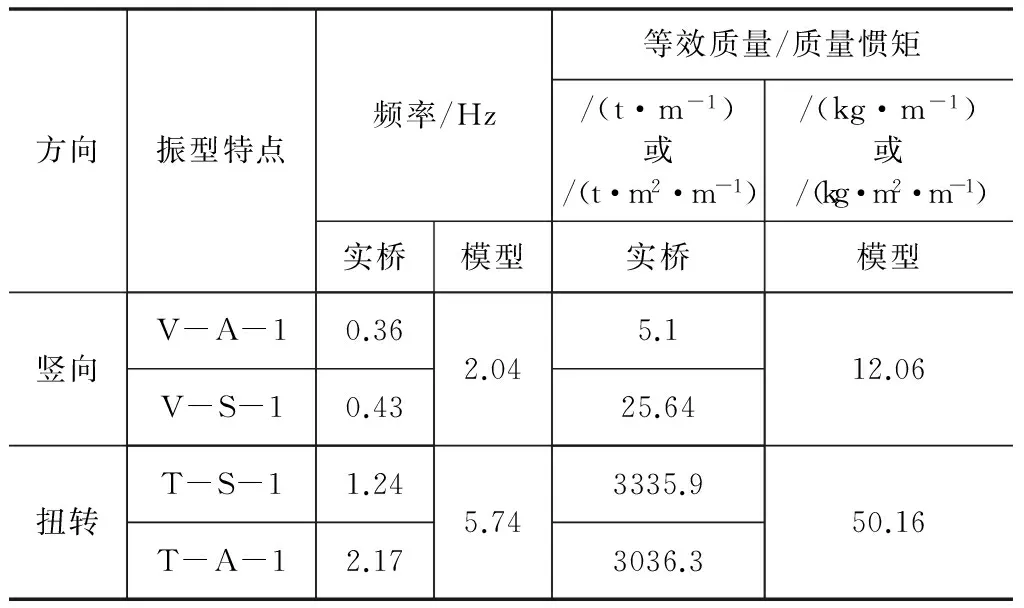
表3 节段模型主要试验参数
注:表3中数字意义同表2。

图6 动力试验的节段模型
试验在均匀流中进行,模型系统的阻尼比取为0.5 %,试验风速比为4.4。分别进行了-3°、0°、+3° 三种攻角情况下的试验。在试验风速和攻角范围内,主梁成桥阶段和施工阶段都没有发生颤振失稳,也没有发现竖向和扭转涡激振动。
从表4中可以看出大桥主梁在-3°、0°和3° 三个攻角下颤振临界风速均高于颤振检验风速,主梁具有很好的颤振安全性。
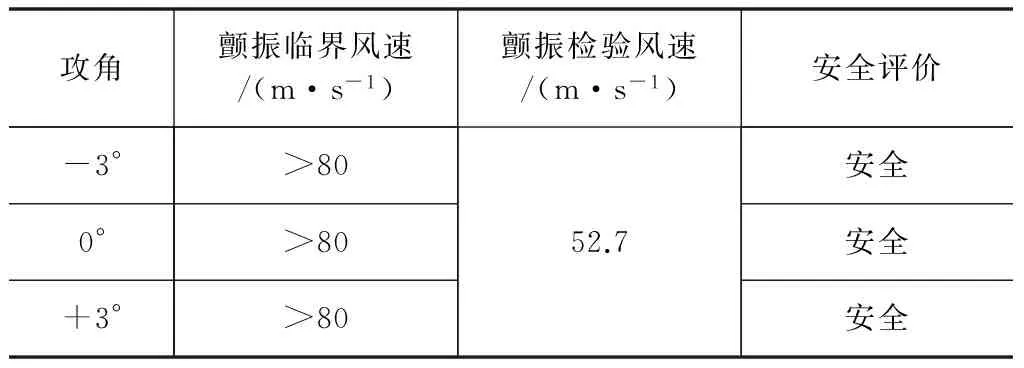
表4 主梁的颤振临界风速
4 全桥气弹模型试验
全桥气动弹性模型能较真实地模拟结构的动力特性,较准确地反映结构与空气的动力相互作用,主要用于检验桥梁结构在均匀来流下的静风稳定、涡振、颤振、驰振等气动性能,以及在紊流条件下的抖振性能等[10]。
考虑到大桥主梁全长以及风洞试验段的尺寸及桥梁结构的规模,将全桥气弹模型的几何缩尺比定为CL=1/20,则气弹模型主跨长14 m,桥塔高1.65 m。安装气弹模型后,风洞中的空气阻塞度小于3 %(一般情况,风洞试验模型在风洞中的空气阻塞度应小于5 %)。
风洞试验中气弹模型由很多段桁架组成,每段桁架之间由弹簧扣来连接,不足的重量由铅块等重物配在石油和天然气管道内。在试验中,利用位移计来测量模型主梁的位移响应,利用贴在桥塔芯梁上的应变片来检测模型桥塔的内力。
根据力学相似理论,用于风洞试验的全桥气动弹性模型应遵循一定的相似准则进行设计,即在原型(实桥)和模型之间保持无量纲参数的一致性,相似准则见表5。
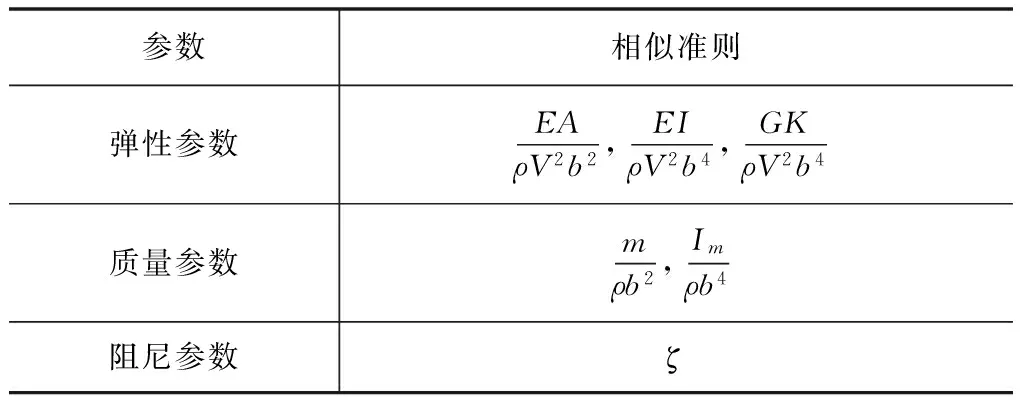
表5 模型设计的相似准则
其中:ρ为空气密度;V为风速;b为结构特征尺度;EA、EI和GK分别为拉压刚度、弯曲刚度和自由扭转刚度;m和Im分别为单位长度的质量和质量惯矩;ζ为结构模态阻尼比。
全桥气动弹性模型由主梁、桥塔、大缆、吊索及支座等构成。其中主梁由很多小段桁架梁段和弹簧扣组成;桥塔部件由芯梁和气动外形组成;大缆由钢绞线提供其刚度并由铁块套在外面控制重量;吊索由没有剪切刚度但拉伸刚度很大的钢丝组成;石油和天然气管道由塑料管里面加铅块配重组成;桥面栏杆用高级塑料板模拟气动外型。安装在实验室中的模型如图7所示。

图7 全桥气弹模型
在进行试验前,首先要进行气弹模型的模态测试,模态测试的目的是检验全桥模型的结构动力特性是否与原型理论计算值之间满足相似关系。模型的动力特性(振型、频率、阻尼)采用用强迫振动法测量。利用激光位移传感器传感器用来获取模型的振动信号。测试所得成桥状态气弹模型的模态结果见表6。从表中可以看出,模型几个重要模态的频率测试值与要求值吻合良好,结构阻尼比也在合理范围内,从而保证了模型结构动力特性与原型相似。全桥气弹模型试验结果见表7。
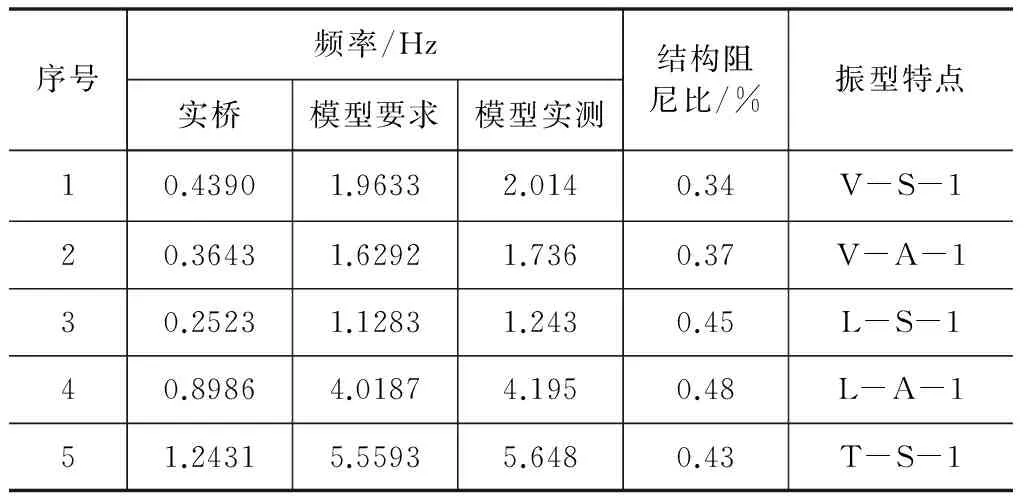
表6 模态测试结果
从表7中可以看出,无论是在均匀流还是紊流中,模型的位移都基本小于50 mm,远小于规范允许的范围,桥梁结构具有很好的抗风安全性。
5 结论
通过桥位风参数计算、节段模型风洞试验、全桥气弹模型风洞试验及结果分析,可得到以下主要结论:
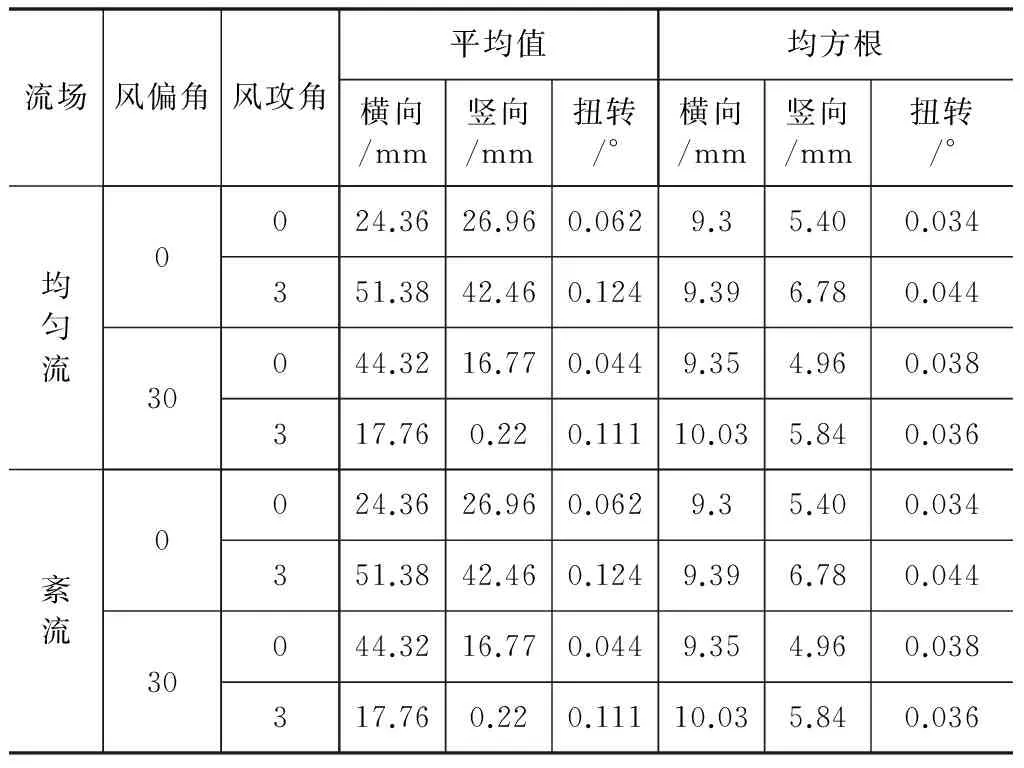
表7 设计风速下的位移响应
(1)大跨管道悬索桥,虽然没有桥面板系统,但是其具有与普通桁架梁悬索桥类似的气动特性,结构动力特性与窄桥类似。
(2)大跨管道悬索桥不同于普通的桁架悬索桥,具有很好的颤振稳定性,不用进行气动外形的优化。
(3)大跨管道悬索桥在设计风速下的位移很小,远小于规范允许值,具有很好的抗风安全性。
(4)管道悬索桥不同于普通的悬索桥,目前没有专门的规范可以采样,在应用于工程实际时,还需通过试验确定桥梁的抗风安全性。
[1] 梁翕章.管道建设的基本规律[J].油气储运, 2003, 22(12):1-9.
[2] 李世荣, 宋艾玲, 张树军.我国油气管道现状与发展趋势[J].油气田地面工程, 2006, 25(6):7-8.
[3] Scanlan R H.Problematic in formulation of wind.force model for bridge decks[J].J Struct.Engrg.ASCE, 1993, 119(7):1433-1446.
[4] JTG/T D60-01-2004 公路桥梁抗风设计规范[S].
[5] 王凯, 廖海黎, 李明水.山区峡谷桥梁设计基准风速的确定方法[J].西南交通大学学报,2013,48(1): 29-36.
[6] 徐洪涛.山区峡谷风特性参数及大跨度桁梁桥风致振动研究[D].成都: 西南交通大学,2009.
[7] 徐洪涛, 廖海黎, 李明水.坝陵河大桥节段模型风洞试验研究[J].世界桥梁, 2009(4): 83-89.
[8] 许福友, 陈艾荣, 张哲.确定桥梁模型颤振临界风速的实用方法[J].振动与冲击, 2008, 27(12) : 97-102.
[9] 胡峰强.山区风特性参数及钢桁架悬索桥颤振稳定性研究[D].上海: 同济大学, 2006.
[10] 王凯, 廖海黎, 刘君.山区峡谷大跨钢桁梁桥抗风特性试验研究[J].振动与冲击,2014,33(19): 169-174.
国家自然科学基金(51278435)
U441.3
A
[定稿日期]2016-01-25
[作者信息]王凯(1988~),男,博士,主要从事桥梁工程研究。
