ABAQUS在闸坝三维渗流计算中的应用

2017-01-09夏俊江

四川水利 2016年2期

关键词：闸坝防渗墙水头

夏俊江

(四川省清源工程咨询有限公司，成都，610072)

水力计算

ABAQUS在闸坝三维渗流计算中的应用

夏俊江

(四川省清源工程咨询有限公司，成都，610072)

本文利用Abaqus软件对某闸坝进行三维渗流非线性有限元计算，得到了闸坝渗流场成果；通过后处理，得到了闸坝的等水头线分布情况，基础各部位的渗透水力梯度以及河床基础和两岸绕坝渗流的流量。

ABAQUS软件闸坝三维渗流渗透坡降渗流流量

1 概述

Abaqus软件被广泛地认为是功能最强的有限元软件，可以分析复杂的固体力学结构力学系统，特别能够驾驭非常庞大复杂的力学问题和模拟高度非线性问题。Abaqus软件包括一个丰富的、可模拟任意几何形状的单元库，并拥有各种类型的材料模型库，可以模拟典型工程材料的性能。作为通用的模拟工具，Abaqus除了能解决大量结构(应力/位移)问题，还可以模拟其他工程领域的许多问题。例如热传导、质量扩散、热电耦合分析、声学分析、岩土力学分析(流体渗透/应力耦合分析)及压电介质分析等。

在渗流计算方面，Abaqus能够求解多孔介质的饱和渗流、非饱和渗流及二者的混合问题(渗流自由面计算)。计算过程中可以考虑流体重力的作用，并能够求解流体总体的孔隙压力或超孔隙压力，渗透定律可采用达西定律或更广泛的非线性定律。本文对它在闸坝的三维非线性渗流计算中的应用进行评述。

2 三维渗流场计算基本理论

渗流连续方程是由同一时间流入土体的水量等于土体的体积变化量这一连续条件建立起来的，即：

式中，Vf为渗流平均速度，n为S面的外法线方向，方程采用流体的参照密度ρf0进行无量纲化。

连续方程采用反向欧拉近似法进行时间积分，用有限单元离散时，基本未知量为孔隙水压力。孔隙流体的渗流行为遵循Darcy定律或Forchheimer定律。Darcy定律一般适用于较低的渗流速度，而Forchheimer定律适用于较高的渗流速度，Darcy定律也可以认为是Forchheimer定律的线性形式。

Forchheimer定律的表达式为：

式中，g为重力加速度，K(s,e)是土体渗透参数，β(e)是“速度系数”。当β=0时，上式即为Darcy定律，因此可知，当渗流速度趋于0时，Forchheimer定律转化为Darcy定律。

土体的渗透性与其饱和度与孔隙率相关，我们假定上述两个依赖关系是相互独立的，对于三维情况统一有：

K=ksk

式中，ks(s)给出了饱和度对渗透性的影响，并有ks(1)=1，而k(e)为土体完全饱和时的渗透性。对于各向同性材料而言，k为标量，但仍要写成二阶张量形式，即k=kI。

3 三维渗流场计算模型及参数

3.1 计算模型

三维渗流计算区域建模边界条件为：上游边界距坝轴线约85.0m，下游边界距坝轴线约180.0m，底部边界距坝顶约99.6m；坝轴线方向，左岸边界距河道中心线约106.5m，右岸边界距河道中心线约83.0m。

进行三维实体建模时，考虑到本计算不涉及结构内部及地基应力的计算，在不影响计算结果的前提下，为了提高渗流计算速度及精度，对坝体及基础进行了适当简化。

因不考虑渗流与应力场的耦合，计算时选择渗流/应力藕合单元，并将单元x、y、z三个方向上的自由度进行约束，对计算区域的网格剖分共计C3D8RP单元11386个，结点总数13125个。整体计算网格剖分如图1所示。

图1 某闸坝三维渗流计算整体网格

3.2 各部位渗透系数取值

计算区域各部位达西渗透系数采用值见表1。

表1 某闸坝三维渗流计算渗透系数

3.3 计算工况

某混凝土闸坝拟定的三维渗流计算工况见表2。

表2 某闸坝三维渗流计算工况

4 三维渗流场计算成果分析

4.1 等水头线分布情况

根据渗流场计算结果，选取河道中心剖面(桩号K0+053.00m)及水平剖面(高程2830.00m)两个典型剖面绘制各工况渗流等水头分布云图(图2～图5)。

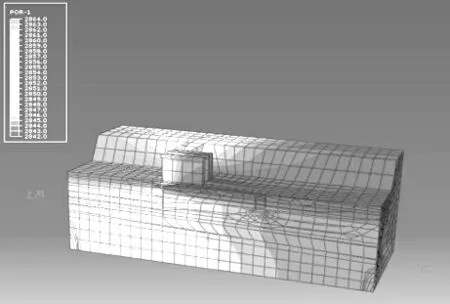
图2 工况1河道中心剖面(桩号K0+053.00m)等水头分布云图(单位：m)

图3 工况1水平剖面(高程2830.00m)等水头分布云图(单位：m)

图4 工况2河道中心剖面(桩号K0+053.00m)等水头分布云图(单位：m)

图5 工况2水平剖面(高程2830.00m)等水头分布云图(单位：m)

4.2 渗透坡降

根据材料渗透强弱的不同，本计算选取混凝土防渗墙、灌浆帷幕及地基(①中细砂层，②含磦砂卵砾石层，③砂质粉土、粘质粉土层，④含磦砂卵砾石层)等部位绘制各工况下的渗透坡降云图(图6～图11)。

图6 工况1混凝土防渗墙渗透坡降分布云图

图7 工况1灌浆帷幕渗透坡降分布云图

图8 工况1④含磦砂卵砾石层渗透坡降分布云图

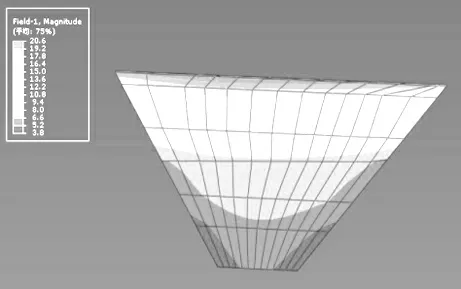
图9 工况2混凝土防渗墙渗透坡降分布云图

图10 工况2灌浆帷幕渗透坡降分布云图

图11 工况2④含磦砂卵砾石层渗透坡降分布云图

防渗体及地基各部位的最大渗透坡降见表3。

表3 某闸坝三维渗流计算各部位最大渗透坡降

从表3可知，在各工况下，防渗墙底部及下游护坦出逸点渗透坡降均小于允许坡降，满足工程相关要求。

4.3 坝基与两岸渗流量

通过在分析步中选择瞬态固结(transient-consolidation)流体响应型式的*SOIL分析步，从输出结果的场输出中选中多孔介质/流体→RVT来获得渗流体积，即渗流流量的值。将坝基河床渗流与两岸边坡渗流区分开来，分别计算各工况下的渗流量，这样能更加清楚地了解坝基渗流与两岸坝肩绕坝渗流两个方面的情况，然后累加各区的渗流量，得到各工况下总渗流量(见表4)。

表4 某闸坝三维渗流计算各工况渗流量(单位：m3/s)

由表4可知：(1)正常蓄水位(工况1)时，通过河床、左岸及右岸的渗流量分别点总的渗流量的88.5%、7.9%和3.6%，总的渗流量占枯期流量的0.86%<1%，满足工程的相关要求；(2)在防渗墙出现开裂失效(工况2)的情况下，渗流量明显增大，由0.203m3/s增大到0.473m3/s，增幅约232.7%，总的渗流量占枯期流量的2.01%>1%，不能满足工程的相关要求。