权利不对等下工程供应链合作收益分配策略研究
2017-01-09赖礼邦
杨 洁,赖礼邦
(1. 福建农林大学管理学院,福建 福州 350002,E-mail:yangjie802@126.com;2.福建船政交通职业学院,福建 福州 350007)
权利不对等下工程供应链合作收益分配策略研究
杨 洁1,赖礼邦2
(1. 福建农林大学管理学院,福建 福州 350002,E-mail:yangjie802@126.com;2.福建船政交通职业学院,福建 福州 350007)
收益分配是涉及合作局中人切身利益的关键问题,当前关于工程供应链合作收益分配问题研究主要基于局中人权利对等假设,但现实中由于各局中人拥有优势资源程度或地位不同,权利不对等现象普遍存在。通过引入收益分配影响因子、依赖权利指数,以及考虑工程供应链合作结构及其所处地位差异,提出修正Shapley值法和A-T解法研究权利不对等下的工程供应链合作收益分配策略。研究表明各局中人的获利能力不仅取决于它对联盟收益的边际贡献程度,也取决于它所在联盟的结构及其所处的具体位置。
工程供应链;收益分配;权利指数;限制结盟;合作博弈
工程供应链是供应链管理研究的一个热门领域,工程供应链相关主体包括原材料供应商、物资供应商、施工分包商、施工总包方、物流服务商、业主等。当前工程供应链合作伙伴关系研究重点关注于供应链前端,主要涉及客户、咨询企业和主要承包商的关系,很少涉及供应链后端诸如子承包商、施工方等在工程建设过程中的影响[1,2]。供应链上下游企业围绕产品设计、生产、销售等价值链增值过程的合作,能有效整合内外部优势资源,增加整体收益[3]。工程供应链合作具有相同的本质,其收益增值效果也不例外。
由于收益分配问题涉及成员的切身利益,直接影响联盟的形成与稳定性,因此相对于其他众多管理问题,收益分配是其关键问题。近年来,国内外不少学者研究了供应链合作收益分配问题。Blecke等[4],以及Mody[5]认为采用平均分配收益的方式容易导致投机行为,因此不宜采用这种收益分配方式。Amaldoss[6]研究发现同功能研发联盟中的收益分配方式对联盟成员的投资策略影响甚微,但在并行研发联盟中,由于投机行为的存在,平均分配收益所获得的联盟成员投入量始终低于按投入比例分配方式联盟成员的资源投入量。从研究内容上,已从两级供应链研究发展到三级,甚至是四级供应链[7]。从研究方法来看,一种主要是运用Stackelberg博弈方法建立利润博弈分配模型并分析其影响作用[8];另一种是运用合作博弈理论的Shapley值法以及其方法修正的合作收益分配[9,10]。王朋等[11]通过引入资源投入、风险分摊和利益相关者满意度因素对Shapley值法进行改进以进行输电工程收益的分配研究。
以上相关研究主要基于局中人权利对等假设,局中人之间可自由结盟且地位完全平等。但现实工程供应链合作过程中,由于参与者(局中人)之间受到资源、技术等因素的影响,其合作中地位的不完全平等性十分普遍,如相互依赖程度不一致,以及投入资源的稀缺性、不可模仿不同。此外,国外大多数相关理论研究普遍认同以总承包商为核心主体,少数是以项目业主或者代表业主的项目公司为核心主体[12]。这就反映出局中人联盟地位不一致,核心主体是联盟组建的关键,不可或缺,具有明显的非自由结盟权利不对等。但当前工程供应链合作文献中,甚少对权利不对等问题及相应收益分配进行深入研究。
因此,本文基于合作分配原则,分别对自由结盟和非自由结盟两类权利不对等情景进行分析,并通过引入收益分配影响因子、依赖权利指数,以及考虑工程供应链合作结构及其所处地位差异,提出修正Shapley值法和A-T解法研究权利不对等下的工程供应链合作收益分配策略。
1 工程供应链合作收益分配模型构建原则
由于工程供应链合作联盟是由多个独立利益主体组成,各方为了实现各自目标或收益的最大化,须考虑各种可能的合作行动方案,并力图选取对自己最为有利的合作方案。但需强调,工程供应链合作并未本质改变成员间的独立利益主体竞争关系,追求自身利益最大化还是其首要的目标,此时竞争关系具体体现于合作收益的分配问题中。因此,工程供应链合作收益分配是典型的多人合作博弈问题,而合作收益分配问题实质上是合作博弈的求解问题。
分配是指将合作产生的支付v在各合作成员间进行分配的方式及结果,一个合作一般存在多个可行收益分配。合作博弈(N,v)需要按一定原则在众多可行收益分配方案中选择合理分配,使得所有合作成员都能够接受,此时的分配称为合作的解。若各参与人从合作的收益中各自分得份额为n维向量x=(x1,x2,…,xn),x为合作博弈(N,v)的分配,其中xi(i=1,2,…,n)表示第i个参与人所得分配值,要求满足如下原则:
(1)个体合理性原则:xi≥v(i),即各局中人参加合作得到的收益不小于其单干所得收益。
2 自由结盟情景中的权力不对等及其收益分配
2.1 自由结盟情景中的权利不对等
自由结盟情景中,任何工程企业可自由结盟,联盟地位平等,权利不对等主要来源于资源贡献度。贡献包括资源投入,如资金、物料等有形资产,以及管理经验、知识产权等无形资产的投入。此外,常说的“多劳多得”也属于此范畴。贡献与收益成正比是分配的常见规则。由于各盟员企业在整个联盟的运作过程中所负责的工作不同,对联盟的贡献也有所不同,因此分配联盟收益时所得多少也应有所不同,这样才能更好地激励盟员企业的工作积极性,提高投入贡献程度。因此,在进行工程供应链合作收益分配时应该对联盟成员的贡献进行科学的评估,并对其做出的贡献有所回报。
此外,由于工程供应链合作过程中存在许多不确定的潜在风险,因此在制定收益分配策略时,需要考虑成员获得的收益与承担风险之间的关系。一般来说,盟员企业承担的风险越大,所得的收益也应越大,否则盟员企业会回避风险,消极承担有风险的任务,无法保证各成员参与联盟的积极性。
特别需要指出,资源投入、风险承担贡献以外,还有一种重要的“权利”贡献。权力是指联盟一方控制和影响另一方行为的能力。当前,相关研究多在于权利指数的研究。权利指数指每个局中人在决策形成获胜联盟中的“关键加入者”个数,“关键加入者”就体现出此局中人的关键权利地位。目前常见的权力指数是Shapley-shubik权力指数。在实际结盟合作博弈问题,当涉及局中人群体决策时,需要局中人投票决定决策结果时,对于简单比较每个局中人的资源贡献,Shapley-shubik权力指数更能实际地客观地反映局中人的权力[13],或者说在达成某项决策时某一局中人的话语权,影响力。但Shapley-shubik权力指数过于突出“关键加入者”的局中人地位,忽视其他局中人的作用。例如:若一局中人一旦拥有超过50%的股份,那么他的Shapley-shubik权力指数为1,而其他股东的Shapley-shubik权力指数为0。但现实中,其他股东还是有部分权力可以行使,此类权利指数不能有效刻画现实情形。
2.2 修正Shapley值的收益分配方法
Bowersox等[14]认为联盟合作中的权力源于合作成员所感知到的相互依赖程度,权力是依赖关系的结果。依赖的产生来源于组织收益与伙伴的相关程度和伙伴的可替代性,高的依赖意味着组织依赖于当前的合作伙伴。在非对称性的关系中,即权利地位不对等的合作关系中,合作双方的收益变得不一致,强权的一方可以使用自身的相对权利获得对方的服从于合作,而相对依赖的一方则担心对联盟承诺会使自身在对方的机会主义行为面前处于弱势地位,因此他们都不愿意增加对合作关系的承诺。为了更为公正客观地体现各局中人的权利,本文引入“依赖权利指数”进行权利大小的刻画,以对Shapley值法进行修正。
对于合作博弈(N,v),称向量φ(v)= (φ1(v),φ2(v),,φn(v) )为合作博弈的经典Shapley值向量,第i个局中人的收益分配值具体为[15]:
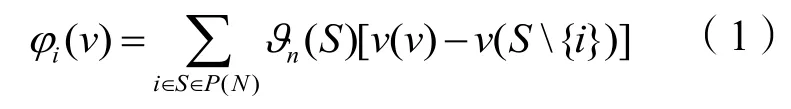
其中,ϑn(S)=(|S|-1)!(n-|S|)!/n!表示不同联盟出现的概率,n为局中人集合N中的元素个数,|S|表示联盟S中成员的个数。v( S)-v( S{i} )可以理解为局中人i对联盟S的边际贡献。
经典Shapley值是按照各个局中人的边际贡献来分配联盟的收益,体现了分配的合理性和公平性。但此研究前提是各个节点企业加入联盟的意愿是一样的,即每个节点企业对其他企业的依赖程度是均等的,都为1 n,没有考虑到各个节点企业的依赖程度是不同的,也就不存在权利不对等情形。徐秋爽等[16]也曾指出Shapley值只能体现那些带来利润多寡的因素,不能体现在因素上的优劣差异。
设各个节点企业想要加入联盟的意愿为Pi,节点企业i对其他节点企业的依赖程度为di,Pi是关于di的函数:
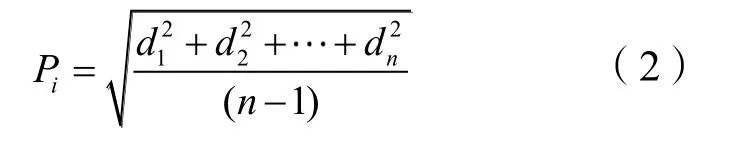
节点企业i参与联盟的意愿为:
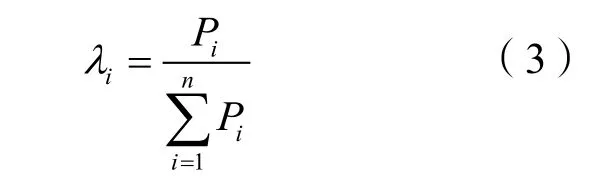
则节点企业i加入联盟的实际意愿与理想状况下的意愿差值为:

为了使各节点企业均愿意加入联盟,对各节点企业进行权利收益激励,假定各节点企业均可以接受的激励因子为θ(0<θ<1),则节点企业i的实际收益分配的修正量为:Δφi(v )=Δλi·θ· φN(v),实际分配的收益为:
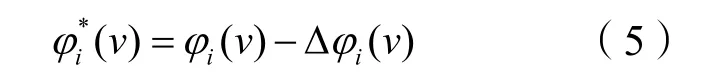
当Δλi>0时,Δφi(v )>0,节点企业i加入联盟的意愿比平均水平要高,对其他企业依赖程度较高,即权利地位偏低,实际收入应从理想收益中扣除Δφi(v),该节点企业实际可分得的收益为:φi*(v)=φi(v)-Δφi(v)。反之,当Δλi<0时,Δφi(v )<0,节点企业i的依赖程度较低,应增加其权利收益Δφi(v),实际分得收益为:φi*(v)=φi(v)+Δφi(v)。
3 非自由结盟情景中的权利不对等及其收益分配
3.1 非自由结盟结构的权利不对等
工程供应链是工程建设方根据客户的特殊需求,由物料、设计、施工并形成最终工程以交付客户的一个整体网络结构。一条完整的工程供应链包括工程供应链相关主体,即原材料供应商、物资供应商、施工分包商、施工总包方、物流服务商、业主等。
工程供应链通常以各分包商提出原材料的需求计划为源头,业主(总承包商)对需求计划进行审批汇总,并根据汇总的需求计划制定各个供应商的供货计划。供应商根据业主下达的供货计划,组织原材料并运输至中转仓库。承包商根据工程现场施工需要,提出原材料调拨计划并提交给业主(总承包商)处,经过审批后领取物资到预制品制造商现场仓库,如图1所示。

图1 工程供应链的基本架构
供应链上各个环节的活动都紧紧围绕着产品的价值增值过程,链上各层级成员都可抽象成一个点,即节点。可见,组成供应链的各纵向节点是以一定的方式和顺序联结成的,具有线性连接的特点,仅有相邻节点间有直接联系,不是任意节点间都可实现价值增值的合作。这是由于不同节点上的特有资源不同,技术间的匹配程度不同,越是具有直接供求关系的相邻节点的技术匹配程度越高,技术溢出效应越是明显。工程供应链中,只有存在直接或间接交流关系的节点企业之间才能合作。这本质反映出以点表示企业(局中人)、以边表示企业(局中人)之间的合作关系的结构。
3.2 A-T解法的收益分配方法
传统合作博弈基于联盟局中人可任意结盟假设(如Shapley值法),这相对于复杂的现实经济管理活动显得过于理想。A-T解能有效反映只有存在直接或间接连通的局中人才能合作的情形[17,18],此分配方式既不是平均分配,也不同基于投资成本的比例分配,而是基于合作各方在合作经济效益产生过程中的重要程度和边际贡献大小来进行收益分配的一种分配方式。A-T解法的具体模型为:
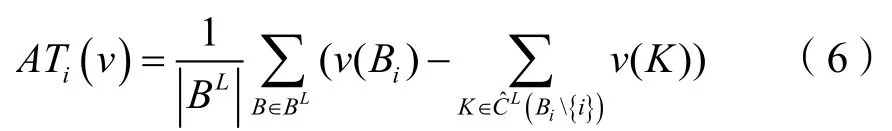
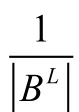
在限制结盟情形下,A-T解法也可类似于Shapley值进行影响因子的修正处理,不再累述。需明确,本文所提出的两种方法都适用于权利不对等工程供应链合作收益分配策略研究,但适用情况有所区别:基于贡献度的联盟权力不对等是针对工程供应链成员间可自由结盟情形,强调因其投入、承担风险或依赖程度不同而体现的权利不对等;而基于限制结盟结构的权力不对等针对工程供应链成员间不能自由结盟情形,强调因联盟结构和所处联盟位置差别而带来的权利不对等。
4 数值算例及分析
4.1 自由结盟的权力不对等收益分配
某工程供应链内上游、中游和下游企业(分别用1,2,3代表),各企业可单干也可组建合作联盟,可能形成的联盟有{1,2}、{1,3}、{2,3}和{1,2,3}4种结盟情形。在投入资源既定的情况下,各合作情形收益分别为:v({1})=30,v({2})=40,v({3})=50,v({1,2})=100,v({1,3})=110,v({2,3})=120,v({1,2,3})=200。此外,各个节点企业对其他节点企业的依赖程度如表1所示。

表1 各企业对其他节点企业的依赖程度
假设各节点企业可以接受的激励因子为20%,根据式(2)~式(5),可求得各个节点企业加入联盟的意愿,以及修正后的收益分配值,如表2所示。
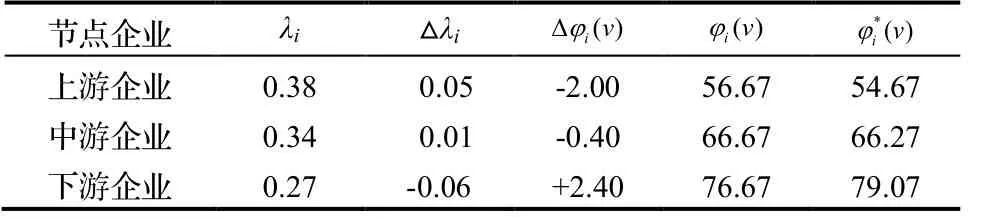
表2 修正前后的收益分配值对比
4.2 非自由结盟的权利不对等收益分配
由于非自由结盟的限制结盟结构,算例4.1中可能形成的合作联盟为N={1,2,3},L={{1,2},{2,3}},即不存{1,3}的情形。此时,根据式(6)可求得具有限制结盟工程供应链的三方成员收益分配值,详见表3。
具有限制结盟结构的权利不对称收益分配,强调上游企业和下游企业之间不存在交流,即两者之间不存在合作可能。Kemahlioglu等[9]和李柏洲等[10]对于此种情况,假设两者之间存在合作,且擅自认为合作收益为单干收益之和,即给出了合作的收益v({1,3})=v({1})+v({3})。基于此假设,运用Shapley值方法进行收益分配,结果如表3所示。
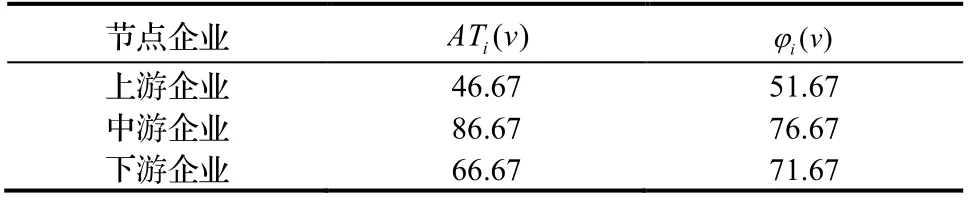
表3 自由结盟与非自由结盟的收益分配值对比
通过对比两种收益分配结果,可知AT1( v)<φ1(v)、AT2( v)>φ2(v)、AT3( v)<φ3(v),表明A-T解法相对于Shapley值法,中游企业的分配收益有所增加,而上游企业和下游企业的分配收益有所减少,这是因为中游企业的无可替代的关键地位。由此可见,在具有限制结盟结构的工程供应链合作中,各节点企业的获利能力不仅取决于它对工程供应链合作收益的贡献,还取决于企业所在工程供应链的结构形式及其在工程供应链中所处的位置。Shapley值法与A-T解法结论之所以不同,源于Shapley值方法中v({1,3})=v{1}+v{3}的假设已改变了上游企业和下游企业限制结盟结构的特点,认为企业间的合作行为是任意,并将不真实存在的收益值参与分配。因此,在具有限制结盟情形下,A-T解相对于Shapley值更具科学合理性。
5 结语
本文针对自由结盟情景的权利不对等和非自由结盟情景的限制结盟结构的权利不对等两种情形,首先对联盟权利不对等结构的特点进行研究,认为工程供应链企业投入的资源越是稀缺、不可模仿,则该企业在联盟中越处于有利地位。为衡量不同联盟(含局中人)在合作中的权利地位差异,通过引入收益分配影响因子、依赖权利指数,以及考虑工程供应链合作结构及其所处地位差异,提出修正Shapley值法和A-T解法研究权利不对等下的工程供应链合作收益分配策略。研究表明各局中人的获利能力不仅取决于它对联盟收益的边际贡献程度,也取决于它所在联盟的结构及其所处的具体位置。此研究可为现实权利不对等下的工程供应链合作收益分配,以及深入探讨工程项目企业(联盟)综合实力地位差异问题提出新思路。
[1]Saad M,Jones M,James P.A review of the progress towards the adoption of supply chain management(SCM) relationships in construction[J].European Journal of Purchasing&Supply Management,2002,8(3):173-183.
[2]Behera P,Mohanty R P,Prakash A.Understanding Construction Supply Chain Management[J].Production Planning&Control,2015,26(16):1-19.
[3]马丁・克里斯托弗.物流与供应链管理(第4版)[M].北京:电子工业出版社,2012.
[4]Blecke J,Ernst D.The way to win in cross-border alliances.Harvard Business Review,1991,69(6):127-135.
[5] Mody A.Learning through alliance.Journal of Economic Behavior and Organization,1993,20(2):151-170.
[6]Amaldoss w.Collaboration to compete.Marketing Science,2000,19(2):105-126.
[7]胡盛强,张毕西,关迎莹.基于Shapley值法的四级供应链利润分配[J].系统工程,2009,27(9):49-54.
[8]邹 艳,陈宇科,董景荣.三级供应链内中游企业纵向合作研发策略[J].管理工程学报,2011,25(1):216-220.
[9] Kemahlioglu Z E,Bartholdi J J.Centralizing inventory in supply chains by using Shapley value to allocate the profits [J].Manufacturing&Service Operations Management,2011,13(2):146-162.
[10]李柏洲,罗小芳.基于Shapley值法的产学研合作型企业原始创新收益分配研究[J].运筹与管理,2013,22(4):220-224.
[11]王 朋,刘 婷,孙海森.输变电工程利益相关方利益均衡分配研究[J].工程管理学报,2015,29(5):114-119.
[12]李 民,高 俊.工程供应链管理研究综述[J].工业技术经济,2012(5):28-37.
[13]谭春桥,张 强.合作对策理论及应用[M].科学出版社,2011.
[14] Bowersox D J,Cooper M B.Strategic marketing channel management.New York:McGraw-Hill,1992.
[15] Shapley L S.Avalue for n-persons games[J].Annals of Mathematics Studies,1953,28:307-318.
[16]徐秋爽,胡石清,程细玉.Shapley值特点及其局限的讨论[J].数学的实践与认识,2013,43(4):44-52.
[17] Herings P,van der Laan G,Talman D.The average tree solution for cycle-free graph games[J].Games and Economic Behavior,2008,62(1):77-92.
[18]杨 洁,李登峰.具有交流结构的区间模糊联盟合作对策[J].计算机工程与应用,2015,51(4):17-21.
Research on Profit Distribution Strategy of Supply Chain Cooperation with Unequal Power
YANG Jie1,LAI Li-bang2
(1. College of Management,Fujian Agriculture and Forestry University,Fuzhou 350002,China,E-mail:yangjie802@126.com;2. Fujian Chuanzheng Communications College,Fuzhou 350007,China)
Income distribution is a crucial problem in cooperation,which relates to player’s vital interests. At present,research on the income distribution in supply chain alliance have made some achievements,but are mainly based on the assumption that players have equal power. However,it’s not truth in fact. There is a generally unequal power characteristic because of different resources,status and so on. By introducing income distribution influence factors,dependent power index,and considering the players’ position,this paper proposes the improved Shapley value method and A-T method to analyze the income distribution strategy of supply chain alliance with unequal power. This study will prove that the profit abilities of supply chain enterprises not only depend on their marginal contribution,but also depend on the alliance's structure and their location.
construction supply chain;income distribution;power index;restricted coalition;cooperative game
F274
A
1674-8859(2016)06-033-05
10.13991/j.cnki.jem.2016.06.007
杨 洁(1985-),女,博士,讲师,硕士生导师,研究方向:经济管理决策与对策(博弈),供应链管理;
2016-05-14.
国家自然科学基金项目(71403055);福建省自然科学基金项目(2016J05169);福建农林大学“校杰出青年科研人才”计划项目(xjq201635).
赖礼邦(1984-),硕士,助教,研究方向:工程管理。
