计及不确定因素的多目标分布式电源优化配置

聂宏展，石浩，杨金成，咸英男

(1.东北电力大学电气工程学院，吉林省吉林市 132012；2.国网新疆电力公司电力科学研究院，乌鲁木齐市 830011；3.国网四平供电公司，吉林省四平市 136000)

计及不确定因素的多目标分布式电源优化配置

聂宏展1，石浩1，杨金成2，咸英男3

(1.东北电力大学电气工程学院，吉林省吉林市 132012；2.国网新疆电力公司电力科学研究院，乌鲁木齐市 830011；3.国网四平供电公司，吉林省四平市 136000)

针对分布式能源(distributed energy resource，DER)并网所引起的不确定因素问题，首先建立了各不确定因素的概率模型，以协调分布式电源(distributed generation，DG)投资方、电网公司以及社会公共效益三者之间利益作为出发点，从DG投资效益指标、网损指标及环境指标3个方面建立了多目标数学优化模型。针对不确定因素问题，基于机会约束规划进行了概率潮流计算，以检验机会约束条件。提出一种基于蒙特卡洛模拟的多目标粒子群优化算法(multi-objective particle swarm optimization algorithm based on Monte Carlo simulation，MPSO-MCS)进行DG优化配置。最后以IEEE 33节点系统作为算例进行仿真，仿真结果表明，考虑分布式能源不确定因素能够更贴近实际地进行分布式电源的优化配置，针对规划后的结果从概率的角度分析系统网损及电压的波动情况，验证了所建立模型及方法的有效性及合理性。

分布式电源(DG)；不确定因素；概率潮流；机会约束规划；多目标粒子群优化算法(MPSO)

0 引 言

随着智能电网的发展及节能减排政策的大力推行，分布式电源(distributed generation，DG)和可入网电动汽车(plug-in electric vehicle，PEV)等分布式能源(distributed energy resource，DER)的接入将作为今后智能配电网规划的重要考虑因素[1]。然而，在分布式能源并网过程中，由于风、光等自然因素间歇性导致的DG出力不确定性以及PEV充电功率的随机性等使得DER具有分散性、随机性、波动性等特点，这些必将给配电网规划带来诸多挑战。同时，如若对DG配置不合理，必将导致配电网供电可靠性下降、潮流反向以及电压稳定性差等。因此，综合考虑DER的各种不确定因素，对DG并网进行合理的优化配置具有重要意义。

近年来，针对分布式电源的优化配置问题，国内外已有学者进行了大量研究。文献[2-3]结合改进的启发式算法进行DG选址定容，但在规划过程中没有考虑风、光等DG出力的随机特性，规划结果与实际情况不符。文献[4]考虑了负荷及风、光出力的时序特性。文献[5]对不同季节的DG出力进行了多场景划分，然后进行多状态划分加权求和得到目标函数期望值，其方法实质是将DG的不确定性出力转化为确定的PQ节点，仅进行了确定性的潮流计算，并没有直观地反映系统具体运行时不确定因素对系统电压及网损的动态影响。文献[6]采用蒙特卡洛法进行概率潮流计算以检验机会约束条件，但是规划中仅从电网公司角度考虑，没有考虑环境指标。文献[7-8]综合考虑了电动汽车、风光机组出力等不确定因素，采用机会约束规划，但是对多目标问题仍采用加权求和的方法转化为单目标处理，无法体现多目标函数间相互制约的关系，并不能为决策者从不同角度提供多种解决方案。

针对上述规划方法的不足之处，本文首先综合考虑DG和PEV等DER并网过程中导致的不确定因素，建立对应的概率模型，从DG投资效益指标、环境指标及网损指标3个角度建立多目标优化模型，提出一种基于蒙特卡洛模拟的多目标粒子群优化算法(multi-objective particle swarm optimization algorithm based on Monte Carlo simulation，MPSO-MCS)进行DG优化配置。利用不确定因素的概率模型通过蒙特卡洛模拟进行随机潮流计算以检验机会约束条件，并利用多目标粒子群优化算法进行多目标寻优得到最优的Pareto前沿，最后以IEEE 33节点配电系统为例进行仿真计算，运用概率分析的方法分析系统网损及电压的波动情况，验证所提规划方法的有效性。

1 不确定因素的概率模型

1.1 风力出力不确定性模型

风速的大量实测数据表明其变化大致服从双参数的威布尔(Weibull)分布，对应的概率密度分布[9-10]为

(1)

式中：v为实时风速；k和c分别为威布尔分布的形状参数和尺度参数。

由风速的概率分布可得到风电源的有功功率输出模型为

(2)

式中：Pwind为风电源输出的有功功率；vci为切入风速；vco为切出风速；vr为额定风速；Pr为风电源的额定输出功率；系数k1和k2为常数，k1=Pr/(vr-vci)，k2=Prvci/(vci-vr)。

1.2 光伏出力不确定性模型

光伏电源的出力会受太阳能电池板温度、太阳光照强度等因素影响而呈现出不确定性，其中光照强度产生的影响最大，而光照强度近似服从beta分布，由光照强度的概率密度曲线，可得到光伏电源输出功率的概率密度曲线为[11]

(3)

式中：Psolar为光伏电源输出的有功功率；Γ为Gamma函数；α、β均为beta分布的形状参数；Psolarm为太阳能电池方阵输出的最大有功功率，Psolarm=rmaxAη，A为方阵总面积，η为总体转换效率，rmax为最大光照强度，W/m2。

1.3 负荷及电动汽车充电不确定性模型

依据美国交通部对全美家庭用车调查结果，得到PEV日行驶距离及最后一次出行时间的概率分布近似服从对数正态分布及威布尔分布[12]，本文主要把私家电动汽车常规充电作为研究对象，其充电行为采取无序状态充电[7]。由中心极限定理可得充电汽车总体充电功率的概率分布近似服从正态分布，详细推导过程可参考文献[13]。

(4)

式中：PEV表示电动汽车充电功率；σEVt表示标准差；μEVt表示在t时刻充电汽车的充电功率期望值。

2 DG多目标优化配置模型

本文建立采用机会约束规划法的多目标数学模型，以协调分布式电源投资方、电网公司以及社会公共效益三者之间利益为基础，综合考虑DG投资效益指标最大、环境指标最小、网损指标最小的DG优化配置。

2.1 目标函数

2.1.1 DG投资效益指标

从分布式电源投资方角度，将单位分布式电源投资所获年收益作为DG投资效益指标[14]。

(5)

式中：ETPF为投资DG折合到每年的收益，ETPF包括DG卖电所获效益以及政府对新能源建设进行的政策类相关补贴；EINV为将投资DG折合到每年的年投资成本，EINV包括DG安装成本、运行及维护成本和燃料耗费等。具体数学模型为：

(6)

(7)

式中：NDG表示DG接入数；ESi为接入节点i处的DG的并网电价；EBi为接入节点i处的DG的政府补助电价；SDGi表示接入节点i处的DG安装容量；λi为容量系数；χDGi为水平年内DG投入金额折合系数；ETi为接入节点i处的DG的单位投入金额；EFi为DG单位的用电量所需维护费及该类型DG的燃料费。

2.1.2 环境指标

从社会公共效益角度，考虑到分布式电源发电产生的污染物(如CO2，NOx，SO2，CO等)对环境产生的影响，建立的环境指标为

(8)

式中：N表示负荷节点数；NDG为DG总数；Ng为产生污染物的类型数；SDGip为第i个节点上第p类DG的出力；wk为第k类污染物所占的权重；Opk为第p类DG单位出力时第k种污染物排放量；αp为碳排放相对值系数。

2.1.3 系统网损指标

从电网公司的角度，DG的合理接入能对系统网损进行改善，从而提高配电网运行的经济性，建立的系统网损指标为

(9)

式中：Ui、Uj分别为节点i和节点j的电压值；Yij为线路ij的导纳参数；θij、δij分别为线路ij的阻抗角及两端电压相角之差。

2.2 约束条件

2.2.1 等式约束条件

(10)

式中：PDGi和QDGi分别为节点i处所接DG的有功功率及无功功率注入量，本文中均为随机变量；PLi和QLi分别为节点i处有功功率和无功功率总消耗量；Ui和Uj为节点i和节点j的电压幅值；Gij和Bij分别为线路导纳阵中的实部及虚部。

2.2.2 机会约束条件

机会约束规划主要是指在约束条件中含有随机变量，允许决策在极小概率的情况下一定程度上越限，但是约束条件的满足必须不小于一定的置信水平，约束条件在一定程度内作为软约束，这使得其比传统的约束条件更具灵活性[8,15]。本文所采用的机会约束条件为

(11)

式中：Pr{}为节点电压或支路传输功率满足不等式条件的概率；Uimin和Uimax分别为节点i处电压的最小值和最大值；Sij为线路ij的安装容量；Sijmax为线路ij的最大安装容量；α1、α2为机会约束规划设定的满足不越限概率的置信水平[16]。

2.2.3 不等式约束条件

(12)

式中：γ为系统接入DG的总有功出力占总有功负荷的最大比率；SDGimax为节点i的DG的最大安装容量。

3 基于MPSO-MCS的规划算法

3.1 MPSO-MCS算法简介

3.1.1 MCS概率潮流计算

考虑到DER接入配电网时所产生的一系列不确定性因素，因此，应用MPSO-MCS进行规划时首先利用MCS进行配网概率潮流计算，基本步骤为：首先依据DG和PEV的概率模型采取轮转赌盘的抽样模式，通过MCS法进行大量的数字模拟；然后对每组采样值进行确定性的前推回代潮流计算得到模拟实验值；最后将模拟实验值进行统计处理，并将得到的结果进行机会约束条件检验，以确定合理的规划方案[17]。

3.1.2 改进多目标粒子群优化算法

粒子群算法是一种基于种群搜索的启发式算法，其将种群中的每个个体看成无质量和体积的粒子在搜索空间中飞行，用位置来表示潜在解，通过个体及群体间信息交互来影响飞行速度，不断迭代指引群体中粒子朝着可能解方向聚集，公式为：

(13)

(14)

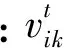
在对多目标算法进行改进中，为了避免过早的收敛于局部最优，本文采用将加速因子c1、c2进行非对称调整策略，同时引入精英父代保存策略和拥挤距离轮赛制策略[18]。基于蒙特卡洛模拟的多目标粒子群优化算法的流程如图1所示。

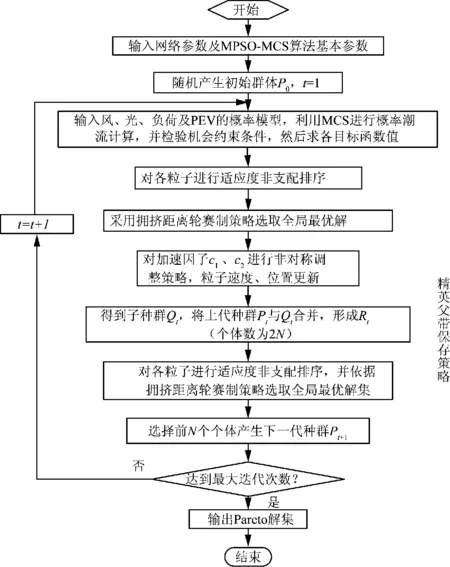
图1 MPSO-MCS算法流程图

3.2 基于MPSO-MCS求解DG优化配置的步骤

(1)输入配电网络原始参数，设定粒子种群规模、最大迭代次数以及MCS抽样次数等参数。

(2)初始化粒子种群，得到初代规划方案。

(3)采用轮盘赌的方式，依据分布式能源概率模型通过MCS法模拟采样，对每一次采样周期进行确定性前推回代潮流计算，以此完成概率潮流计算并利用潮流计算结果检验是否满足约束条件及机会约束条件，若是则进行步骤(4)，否则重新对粒子进行初始化操作。

(4)对粒子进行目标函数值计算，利用改进的MPSO算法获取最优规划解集，判断是否已达最大迭代次数，若达到最大迭代次数则输出最优解Pareto解集，否则回到步骤(3)重新进行概率潮流计算和目标函数值计算并再次运用MPSO寻优，直至满足结束条件，并输出最终的优化配置方案解集。

4 算例分析

4.1 仿真算例原始数据

本文采用MATLAB R2010a综合分析软件来研究DG在配电系统中的优化配置问题。测试算例采用IEEE 33节点配电系统[19]，电压等级为12.66 kV，对应的网络框架结构如图2所示。分布式电源待选接入节点为：风力发电单元(wind turbine generator，WT)待选接入节点为15，17，18号节点；光伏发电单元(photovoltaic，PV)待选接入节点为29，31，32号节点；微型燃汽轮机发电单元(micro-turbine generator，MT)待选接入节点为9，12，14号节点；燃料电池发电单元(fuel cell generator，FC)待选接入节点为26，27，28号节点。分布式电源规划周期水平年为10年，水平年内DG投入金额折合系数参见表1，1个运行决策周期为1年。

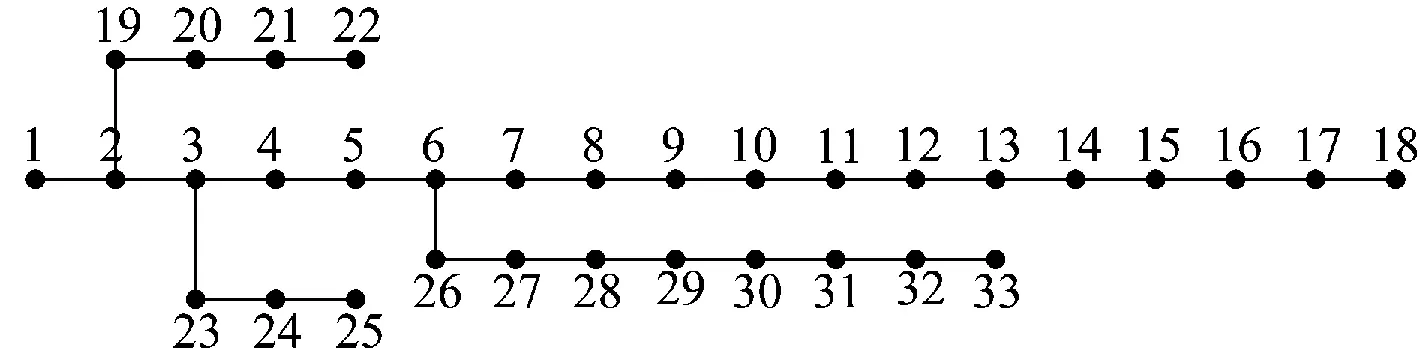
图2 IEEE 33节点配电网系统

采用MPSO-MCS算法进行分析计算，其中MPSO算法中：种群粒子数目为100；最大迭代次数为100；ω变换区间为[0.5，0.8]；非对称变化加速因子c1从2.75到1.25匀步长递减，c2从0.5到2.25匀步长递增；MCS的抽样次数为2 000；节点电压幅值的机会约束置信水平参数设置为0.9；配电系统中分布式电源最大允许的DG渗透率设置为0.4。分布式电源的投资运行等参数如表1所示。

不确定性风、光分布式电源模型参数设置分别如表2和表3所示。假设算例区域共有800辆电动私家车，平均充电功率取2 kW，均匀散布于各节点区域，持续充电约6 h可以将其充满。

表1 不同类型DG投资运行参数

Table 1 Investment and operation parameters of different kinds of DGs

表2 风力发电参数

表3 光伏发电参数

4.2 结果分析

采用本文算法进行分析计算，考虑经济投资效益、网络损耗及污染气体排放指标的分布式电源多目标优化配置的最优Pareto解如图3所示。

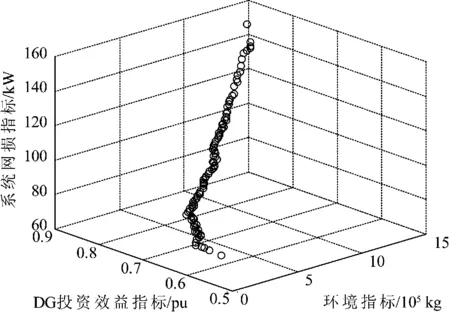
图3 DG多目标优化配置最优Pareto前沿

由图3可知，采用本文多目标优化算法所获取的Pareto前沿分布均匀，说明本文方法具有很好的寻优性能。另一方面，由Pareto前沿可知，系统投资运行效益指标与网络损耗指标和污染气体排放指标近似呈正比关系，说明在分布式电源优化配置过程中良好的经济效益是以牺牲系统运行技术指标与环保效益为代价的。为权衡各目标函数之间的内在联系，从最优Pareto前沿中选取几种具有代表性的方案进行分析计算，不同方案下的相关参数性能见表4所示。

由表4可知，不同方案下DG优化配置结果各不相同。方案A中网损指标相对较优，但是其投资效益、污染气体排放量指标相对较差；方案B中系统投资效益、污染气体排放量指标相对最优，但系统网损指标并非最佳；方案C是采用模糊隶属度技术[20]选择的最佳方案，权衡了各子目标函数，从多角度的方式进行综合评价所获得的较优方案。

为验证DG优化配置后系统电压运行指标的性能，采用概率统计的思想对分布式电源接入节点电压信息进行统计分析，以方案C为例，不同分布式电源接入节点下系统电压运行的概率密度曲线分布如图4所示。

由图4可知，不同节点电压波动范围不同，但采用机会约束的处理手段均能保证系统各节点电压运行在置信区间约束范围之内。另一方面，17号节点和32号节点电压波动范围较大，是因为风、光分布式电源接入节点受间歇性自然资源的影响而导致的。分布式电源接入后系统有功功率及无功功率损耗概率密度曲线如图5所示。

表4 3种方案下DG优化配置结果

Table 4 Optimal configuration results of DG in three schemes

图4 典型节点电压幅值的概率密度曲线

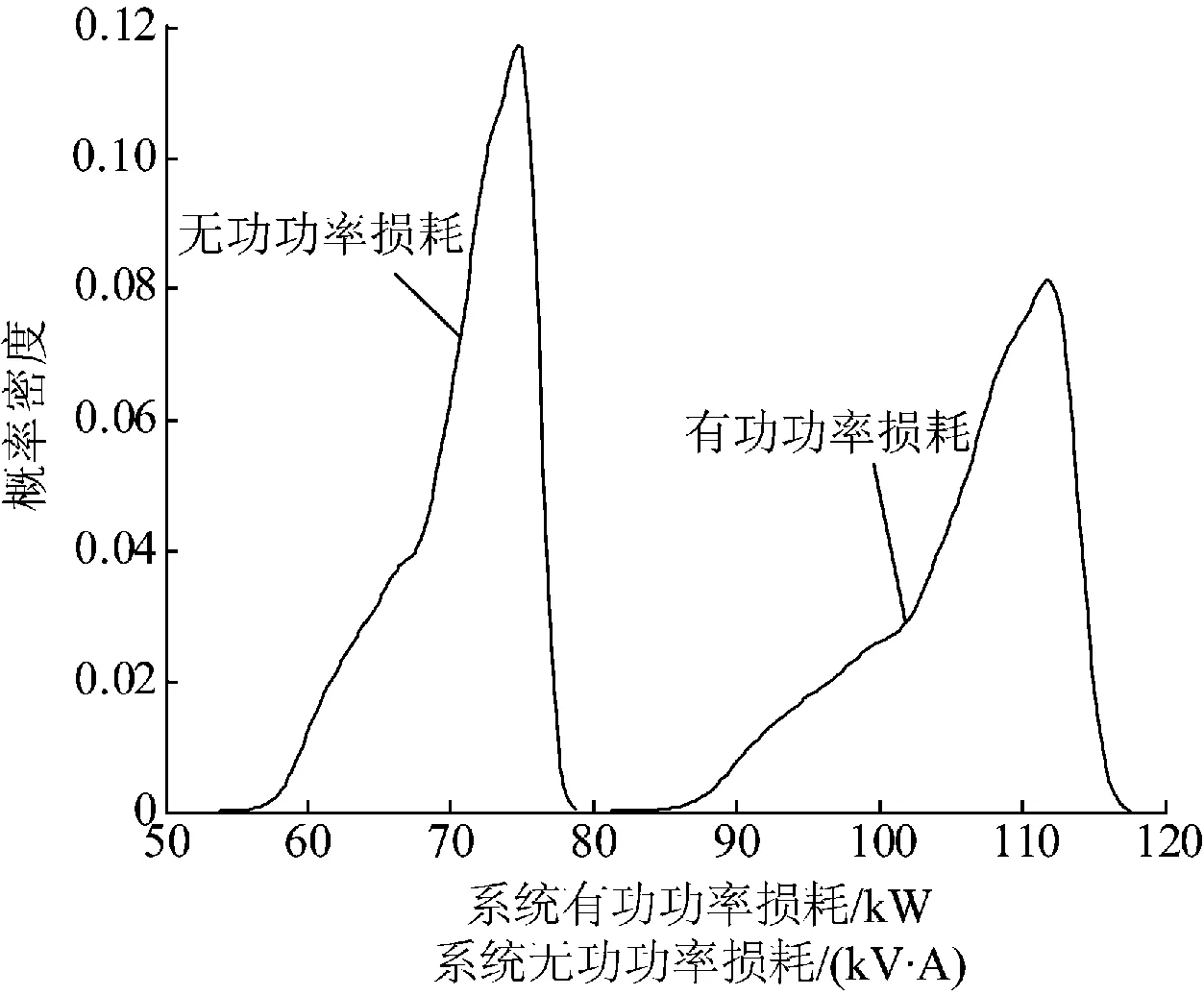
图5 DG接入后系统网络损耗的概率密度曲线

由图5可知，系统有功功率损耗及无功功率损耗变化幅度较大，且与按照DG配置额定出力对比可知，系统有功及无功损耗明显偏大，是因为间歇性分布式电源并未能按其额定安装功率出力所导致的，说明采用本文方法所得的优化配置结果与传统按恒定DG出力的处理手段相比，本文方法所获得的最终配置方案更加合理有效，适用于未来主动灵活配电体系发展的需要。

5 结 论

(1)综合考虑DG优化配置中由分布式能源所引起的不确定因素影响，既能够较好地反映出未来大规模DER并网的特点，又可以满足未来智能电网的发展趋势，对实际工程规划具有指导意义。

(2)采用多目标规划模型能够综合考虑DG优化配置中的各类指标，便于规划人员从不同角度确定最佳规划方案，以达到满意度最高的规划效果。

(3)采用机会约束规划进行概率潮流计算，从符合概率的角度对典型节点电压、系统网损进行了概率分析，统计结果表明运用概率手段展示DG规划方法能更为直观反映出系统实际运行状况，进一步说明规划方法的合理性及优越性。

[1]马钊，周孝信，尚宇炜，等.未来配电系统形态及发展趋势[J].中国电机工程学报，2015，35(6)：1289-1298. MA Zhao, ZHOU Xiaoxin, SHANG Yuwei, et al. Form and development trend of future distribution system[J]. Proceedings of the CSEE, 2015, 35(6): 1289-1298.

[2]范彬，周力行，黄頔，等.基于改进蝙蝠算法的配电网分布式电源规划[J].电力建设，2015，36(3)：123-128. FAN Bin, ZHOU Lixing, HUANG Di, et al. Distributed generation planning for distribution network based on modified bat algorithm[J]. Electric Power Construction, 2015, 36(3): 123-128.

[3] 关添升，王琦，刘赫，等.基于改进果蝇优化算法的分布式电源优化配置[J].电力建设，2016，37(6)：103-108. GUAN Tiansheng, WANG Qi, LIU He, et al. Optimal configuration of distributed generation based on improved fruit fly optimization algorithm[J]. Electric Power Construction, 2016, 37(6): 103-108.

[4]李亮，唐巍，白牧可，等.考虑时序特性的多目标分布式电源选址定容规划[J].电力系统自动化，2013，37(3)：58-63, 128. LI Liang, TANG Wei, BAI Muke, et al. Multi-objective locating and sizing of distribution generators based on time-sequence characteristics[J]. Automation of Electric Power Systems, 2013, 37(3): 58-63, 128.

[5]唐念，夏明超，肖伟栋，等.考虑多种分布式电源及其随机特性的配电网多目标扩展规划[J].电力系统自动化，2015，39(8)：45-52. TANG Nian, XIA Mingchao, XIAO Weidong, et al. Multi-objective expansion planning of active distribution systems considering distributed generator types and uncertainties[J]. Automation of Electric Power Systems, 2015, 39(8): 45 -52.

[6]张沈习，陈楷，龙禹，等.基于混合蛙跳算法的分布式风电源规划[J].电力系统自动化，2013，37(13)：76-82. ZHANG Shenxi, CHEN Kai, LONG Yu, et al. Distributed wind generator planning based on shuffled frog leaping algorithm[J]. Automation of Electric Power Systems, 2013, 37(13): 76-82.

[7]彭显刚，林利祥，刘艺，等.计及电动汽车和可再生能源不确定因素的多目标分布式电源优化配置[J].电网技术，2015，39(8)：2188-2194. PENG Xiangang, LIN Lixiang, LIU Yi, et al. Multi-objective optimal allocation of distributed generation considering uncertainties of plug-in electric vehicles and renewable energy sources[J]. Power System Technology, 2015, 39(8): 2188-2194.

[8]刘志鹏，文福拴，薛禹胜，等.计及可入网电动汽车的分布式电源最优选址和定容[J].电力系统自动化，2011，35(18)：11-16. LIU Zhipeng, WEN Fushuan, XUE Yusheng, et al. Optimal sitting and sizing of distributed generators considering plug-in electric vehicles[J]. Automation of Electric Power Systems, 2011, 35(18): 11-16.

[9]董雷，程卫东，杨以涵.含风电场的电力系统概率潮流计算[J].电网技术，2009，33(16)：87-91. DONG Lei, CHENG Weidong, YANG Yihan. Probabilistic load flow calculation for power grid containing wind farms[J]. Power System Technology, 2009, 33(16): 87-91.

[10]王敏，丁明.考虑分布式电源的静态电压稳定概率评估[J].中国电机工程学报，2010，30(25)：17-22. WANG Min, DING Ming. Probabilistic evaluation of static voltage stability taking account of distributed generation[J]. Proceedings of the CSEE, 2010, 30(25): 17-22.

[11]张喆，李庚银，魏军强.考虑分布式电源随机特性的配电网电压质量概率评估[J].中国电机工程学报，2013，33(13)：150-156. ZHANG Zhe, LI Gengyin, WEI Junqiang. Probabilistic evaluation of voltage quality in distribution networks considering the stochastic characteristic of distributed generators[J]. Proceedings of the CSEE, 2013, 33(13):150-156.

[12]葛少云，王龙，刘洪，等.计及电动汽车入网的峰谷电价时段优化模型研究[J].电网技术，2013，37(8)：2316-2321. GE Shaoyun, WANG Long, LIU Hong, et al. An optimization model of peak-valley price time-interval considering vehicle-to-grid[J]. Power System Technology, 2013, 37(8): 2316-2321.

[13]蔡德福，钱斌，陈金富，等.含电动汽车充电负荷和风电的电力系统动态概率特性分析[J].电网技术，2013，37(3)：590-596. CAI Defu, QIAN Bin, CHEN Jinfu, et al. Analysis on dynamic probabilistic characteristic of power grid connected with electric vehicle charging load and wind power[J]. Power System Technology, 2013, 37(3): 590-596.

[14]张立梅，唐巍，王少林，等.综合考虑配电公司及独立发电商利益的分布式电源规划[J].电力系统自动化，2011，35(4)：23-28. ZHANG Limei, TANG Wei, WANG Shaolin, et al. Distributed generators planning considering benefits for distribution power company and independent power suppliers[J]. Automation of Electric Power Systems, 2011, 35(4): 23-28.

[15]赵书强，王扬，徐岩，等.基于机会约束目标规划的高风电接入比例下大规模储能与火电协调调度[J].中国电机工程学报，2016，36(4)：969-977. ZHAO Shuqiang, WANG Yang, XU Yan, et al. Coordinated dispatch of large scale energy storage system and thermal generation in high wind power penetration level system based on chance constrained goal programming[J]. Proceedings of the CSEE, 2016, 36(4): 969-977.

[16]李振坤，田源，董成明，等.基于随机潮流的含电动汽车配电网内分布式电源规划[J].电力系统自动化，2014，38(16)：60-66. LI Zhenkun, TIAN Yuan, DONG Chengming, et al. Distributed generators programming in distribution network involving vehicle to grid based on probabilistic power flow[J]. Automation of Eletric Power Systems, 2014, 38(16): 60-66.

[17]刘宇，高山，杨胜春，等.电力系统概率潮流算法综述[J].电力系统自动化，2014，38(23)：127-135. LIU Yu, GAO Shan, YANG Shengchun, et al. Review on algorithms for probabilistic load flow in power system[J]. Automation of Electric Power Systems, 2014, 38(23): 127-135.

[18]冯士刚，艾芊.带精英策略的快速非支配排序遗传算法在多目标无功优化中的应用[J].电工技术学报，2007，22(12)：146-151. FENG Shigang, AI Qian. Application of fast and elitist non-dominated sorting generic algorithm in multi-objective reactive power optimization[J]. Transactions of China Electrotechnical Society, 2007, 22(12): 146-151.

[19]AMAN M M, JASMON G B, BAKAR A H A, et al. A new approach for optimum simultaneous multi-DG distributed generation units placement and sizing based on maximization of system loadability using HPSO (hybrid particle swarm optimization) algorithm[J]. Energy, 2014, 66: 202-215.

[20] 栗然，马慧卓，祝晋尧，等.分布式电源接入配电网多目标优化规划[J].电力自动化设备，2014，34(1)：6-13. LI Ran, MA Huizhuo, ZHU Jinyao, et al. Multi-objective optimization for DG integration into distribution system[J]. Electric Power Automation Equipment, 2014, 34(1): 6-13.

(编辑 景贺峰)

Multi-Objective Optimal Configuration of Distributed Generation Considering Uncertainties

NIE Hongzhan1, SHI Hao1, YANG Jincheng2, XIAN Yingnan3

(1.School of Electrical Engineering, Northeast Dianli University, Jilin 132012, Jilin Province, China; 2. Electric Power Research Institute, State Grid Xinjiang Electric Power Company, Urumqi 830011, China; 3. State Grid Siping Electric Power Supply Company, Siping 136000, Jilin Province, China)

According to the influence caused by the uncertainty factors of grid-connected distribution energy resource (DER), this paper firstly establishes a probabilistic model for each uncertainty factors to coordinate the benefits in the investors of distributed generation (DG), grid company and social public; and establishes the multi-objective mathematical optimization model from three aspects of DG investment benefit index, transmission loss index and environmental index. Aiming at uncertain factors, this paper calculates the probabilistic flow based on the opportunity constrained programming to test the constraints condition of opportunity. Then, this paper proposes a multi-objective particle swarm optimization algorithm based on Monte Carlo simulation method (MPSO-MCS) to optimize the DC configuration. Finally, the example simulation results of an IEEE 33 node system show that the proposed model with considering the uncertainty factors of DG can optimize the configuration of DG more close to reality. According to the results after planning, the analysis results of system losses and voltage fluctuations under probabilistic method verify the effectiveness and rationality of the proposed model and method.

distributed generation (DG); uncertainty; probabilistic flow; chance constrained programming; multi-objective paricle swarm opimization algorithm (MPSO)

国家电网公司科技项目(SGXTDKOOTLTS1600154)

TM 715

A

1000-7229(2016)10-0130-07

10.3969/j.issn.1000-7229.2016.10.018

2016-07-13

聂宏展(1962)，男，硕士，教授，主要研究方向为电力系统规划、电力系统继电保护；

石浩(1990)，男，硕士研究生，主要研究方向为电力系统规划；

杨金成(1990)，男，本科，助理工程师，主要研究方向为电气系统自动化、电力计量；

咸英男(1991)，男，本科，助理工程师，主要研究方向为电力系统自动化。