大型光伏电站集电系统谐波传递网络分析

朱永强，郝嘉诚，唐萁，杨慧娜，李春来

(1.新能源电力系统国家重点实验室(华北电力大学)，北京市 102206；2.青海省光伏发电并网技术重点实验室，西宁市 810000)

大型光伏电站集电系统谐波传递网络分析

朱永强1，郝嘉诚1，唐萁1，杨慧娜1，李春来2

(1.新能源电力系统国家重点实验室(华北电力大学)，北京市 102206；2.青海省光伏发电并网技术重点实验室，西宁市 810000)

大型光伏电站中，每组并网逆变器系统的输出功率(电流)经站内集电系统汇集后向外送出。文献研究表明，即使单台并网逆变器的输出电流谐波较小，多台并网逆变器并联后输出电流的谐波也有可能超标。针对典型大型并网光伏电站拓扑结构，建立了详细考虑站内集电系统结构的大型光伏电站谐波传递网络模型。用节点导纳法在MATLAB中对算例进行了谐波潮流计算，得出各个节点各次谐波电压相对于该点基波电压的放大倍数，并选取主变压器低压侧节点作为分析对象，与忽略集电系统内部结构时的计算结果作比对，发现谐波电压放大特性发生明显改变。最后分析了集电系统内部LCL滤波器及电缆线路参数对传递网络谐波电压放大特性的影响。

大型光伏电站；集电系统；谐波；传递网络

0 引 言

2015年，我国新能源发电持续快速增长，光伏装机容量首次超过德国跃居世界第一。据最新的数据统计，截至2015年，我国太阳能发电装机容量达到 4 158万 kW。预计到2020年，我国大型集中式光伏电站将达 8 000万 kW[1]。由于我国太阳能资源主要富集于西北部地区，距离负荷中心较远，需要采用高压远距离输电，因此光伏电站的规模化和大型化已经成为光伏产业的重要发展趋势之一[2]。

随着光伏电站装机容量的爆发式增长，大规模光伏电站的接入及电力电子装置的广泛应用使得大量非线性负载也加入到电力系统中，对电力系统造成污染，出现电能质量问题[3-4]。目前，谐波问题是制约光伏电站并网最主要的问题之一，很多大型并网光伏电站存在谐波超标问题，且在低光照运行条件下更加突出[2]。大型光伏电站中，每组并网逆变器系统的输出电流经站内集电系统汇集后向外送出[5]。有文献研究表明，即使单台并网逆变器的输出电流谐波较小，多台并网逆变器并联后输出电流的谐波也有可能超标[6-7]。由于大型并网光伏电站一般采用LCL滤波器，且很多光伏电站通过长距离输电线缆接入弱电网，滤波电容可能引起谐振从而造成某些次谐波放大[8-12]。因此，在对大规模光伏电站进行谐波分析时，不仅要考虑光伏系统与电网之间日益显著的相互作用，也应当考虑由滤波器、变压器、电缆线路等元件构成的集电系统对谐波传递所造成的影响。

文献[13]的研究结果表明电网阻抗导致系统存在谐振现象，降低系统电能质量，并网点电压的谐波畸变率远大于逆变器输出电流，并网点电压谐波含量更易超标。文献[14]提出了大型光伏电站谐波串并联谐振数学模型，分析了谐波串并联谐振机理，定量分析了谐波电压放大系数及其与输电距离、谐波次数及谐波类型的关系。文献[13]和[14]都从逆变器的控制层面研究了电网阻抗对大型光伏电站谐波及谐振的影响，但在进行网络等效时，并未将大型光伏电站集电系统内部元件及连接方式纳入考虑范围。文献[15]虽然在分析计算时详尽地考虑了光伏电站集电系统的内部结构，但是其研究内容为光伏电站静态电压稳定性问题，与谐波传递网络无关。文献[16]推导出 1 MV·A发电单元戴维宁等效电路，建立了接近实际并网系统的阻抗网络模型，分析了光伏电站谐波输出与辐照度及光伏板温度的关系，但没有讨论模型中各元件参数的变化对谐波输出结果的影响。

本文针对典型大型并网光伏电站拓扑结构，建立详细考虑站内集电系统结构的大型光伏电站谐波传递网络模型。用节点导纳法在MATLAB中对算例进行谐波潮流计算，得出各个节点各次谐波电压相对于该点基波电压的放大倍数，并选取主变压器低压侧节点作为分析对象，与忽略集电系统内部结构的计算结果对比，发现谐波电压放大特性发生明显改变。最后分析集电系统内部LCL滤波器及电缆线路参数对传递网络谐波电压放大特性的影响。

1 谐波传递网络

1.1 大型并网光伏电站结构

大型并网光伏电站结构如图1—3所示。大型光伏电站包含若干光伏发电单元，光伏发电单元的输出功率经站内集电线路汇入10 kV交流母线。假设光伏电站共有m条并联的集电线路，每条集电线路由n个光伏发电单元组成。光伏电站产生的电能经变比为10 kV/121 kV的主变压器升压，通过高压输电线路并入大电网。

图1 大型并网光伏电站结构图

图2 集电线路结构图

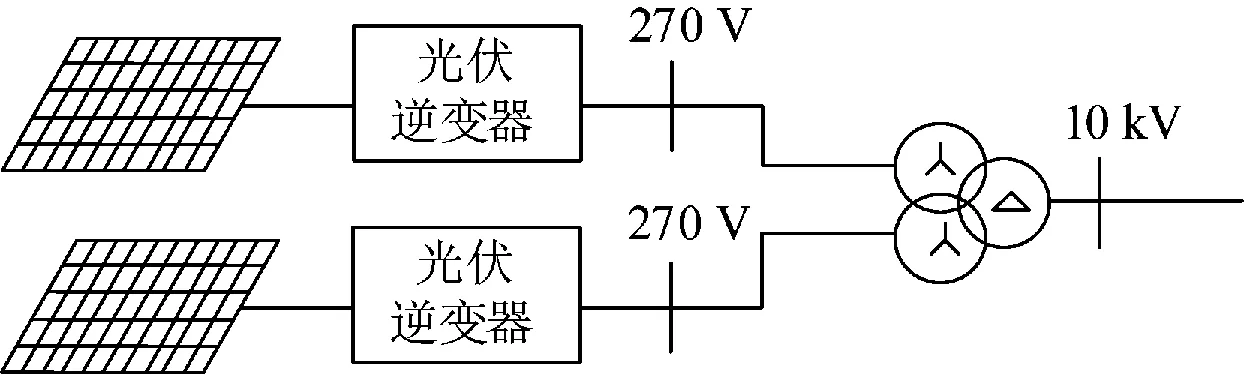
图3 光伏发电单元结构图

1.2 谐波传递网络中各元件等效模型

1.2.1 光伏发电单元

光伏发电单元阻抗图如图4所示。在光伏发电单元中，2组光伏阵列分别与2台500 kW的光伏逆变器连接，逆变器的输出电流经LCL滤波器后送至一台变比为10.5 kV/0.27 kV/0.27 kV的双分裂变压器，然后接入站内集电系统。

图4 光伏发电单元阻抗图

采用电流控制模式的光伏逆变器，在谐波潮流计算中处理为能够输出恒定电流的电流源。光伏逆变器LCL滤波器的谐波阻抗可用式(1)计算。

(1)式中：ZL为电感的谐波阻抗；h为谐波次数；XL为电感的基波电抗；Zc为电容的谐波阻抗；Xc为电容的基波电抗。

光伏发电单元采用短路阻抗百分比为4.5%、额定容量为1 000/500/500 kV·A的双分裂变压器，忽略变压器内部阻抗的影响，有Zt=jXt。若Zt1表示高压绕组的等效阻抗，Zt2、Zt3分别表示2个低压绕组的等效阻抗，通常情况下，双分裂变压器的等效阻抗可以用式(2)计算。

(2)

式中：Xt1为双分裂变压器原边绕组的基波等效电抗；Xt2、Xt3分别为2个副边绕组的基波等效电抗；KF为分裂系数；X1-2为穿越阻抗。

大型光伏电站中每组并网逆变器系统通常采用相同的结构、参数和控制策略等，且升压变压器的型号均相同[14]。因此，假设图1中所有发电单元内各个元件的参数完全相同。

1.2.2 输电线路和电缆

在基波计算时，输电线路通常采用π型等值电路。但是在谐波计算中，由于线路的分布特性比基波时更加显著，因而每个π型所能代表的线路距离将大为缩短。因此在谐波计算中，更多使用的是分布参数等值电路。为使长线路的分布参数等值电路计算更加便利，采用双曲函数来计算输电线路和电缆的等值电路[17]。h次谐波时，线路单位长度的谐波参数为

(3)

式中：Zoh为线路的单位长度谐波阻抗；Roh为单位长度谐波电阻；X1为单位长度基波电抗；Yoh为单位长度谐波导纳；B1为单位长度基波电纳。考虑到集肤效应，线路的单位长度电阻可由式(4)计算。

(4)

式中R1为线路单位长度基波电阻。

h次谐波时，长度为l的输电线路或电缆的阻抗和导纳值为

(5)

式中：ZLh和YLh分别为线路的谐波阻抗和导纳；ZCh和γh分别为h次谐波时线路的特征阻抗和传播函数，可由式(6)计算得到。

(6)

1.2.3 主变压器

在高次谐波的作用下，变压器绕组的集肤效应和邻近效应都变得更加显著，电阻值要增大[18]。本文采用IEEE提出的变压器谐波阻抗模型。

ZT=h1.15RT+hXT

(7)

式中：ZT为主变等效谐波阻抗；RT和XT分别为基波下主变的等效电阻和电抗。

1.2.4 高压电网(系统)与负荷

当高压电网或负荷的功率为S，功率因数为cosφ时，系统或负荷在h次谐波下的等值阻抗为

(8)

式中：Z为系统或负荷的谐波等效阻抗；R和X分别为其基波等效电阻和电抗。

1.3 谐波传递网络模型

图5和图6分别为集电线路阻抗图和大型并网光伏电站阻抗图。假设大型光伏电站集电系统由m条并联支路组成，每条支路共包含n个发电单元，如图5所示。集电系统将各个发电单元所发电能汇集后，经主变压器、高压输电线路送入电网，电力传输网络的等效阻抗如图6所示。

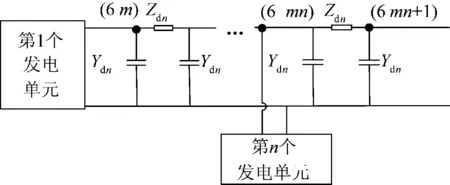
图5 集电线路阻抗图

图6 大型并网光伏电站阻抗图

根据图5和图6所示的谐波传递网络结构，节点导纳矩阵Y为(6mn+3)阶方阵。令k=6mn，则有

(9)

式中Ya为(6n×1)阶列向量。

(10)

Ym为集电线路单条支路的节点导纳矩阵，Ym为6n阶方阵，方阵Y中共有m个Ym矩阵。

(11)

式中：Y1为集电系统单条支路的第1个发电单元及与其相连的电缆的节点导纳矩阵；Y2为该条支路其余各个发电单元及与其相连的电缆的节点导纳矩阵。Y1、Y2均为6阶方阵。为保证Ym的正确性，Yc为Yb的补充矩阵。Y1、Y2、Yc可通过式(12)—(14)求得。

(12)

方阵Y2除Y2(6，6)之外，其余位置的值均与Y1相同，集电系统单条支路第i个(i=2，3，…，n)发电单元的节点导纳矩阵Y2的Y2(6，6)为

(13)

Yc为6n阶对称方阵，有

(14)

需要说明的是，式(12)—(14)矩阵Y1、Y2、Yc未说明的部分均为0。

2 算例分析

2.1 谐波潮流计算

与基波潮流计算类似，谐波潮流计算就是根据各谐波源节点的注入谐波电流和该谐波传递网络节点导纳矩阵组成的网络方程求解各节点谐波电压，即

U(h)=Y-1(h)I(h)

(15)式中：U(h)为各节点h次谐波电压列向量；Y(h)为h次谐波传递网络的节点导纳矩阵；I(h)为各节点h次谐波注入电流列向量。令含谐波源的节点注入电流为单位h次谐波电流，不含谐波源的节点注入电流均为0。

需要注意的是，谐波传递网络中各元件等效阻抗的大小随谐波次数的变化而变化，因此在计算中需要多次形成谐波传递网络节点导纳矩阵。

2.2 2种结构下谐波潮流计算结果对比

在大型光伏电站集电系统中，各发电单元之间的电缆由于线路长度短、电压等级低，因而在某些研究中忽略了电缆参数的影响，认为各个发电单元为简单的并联关系，如图7所示。

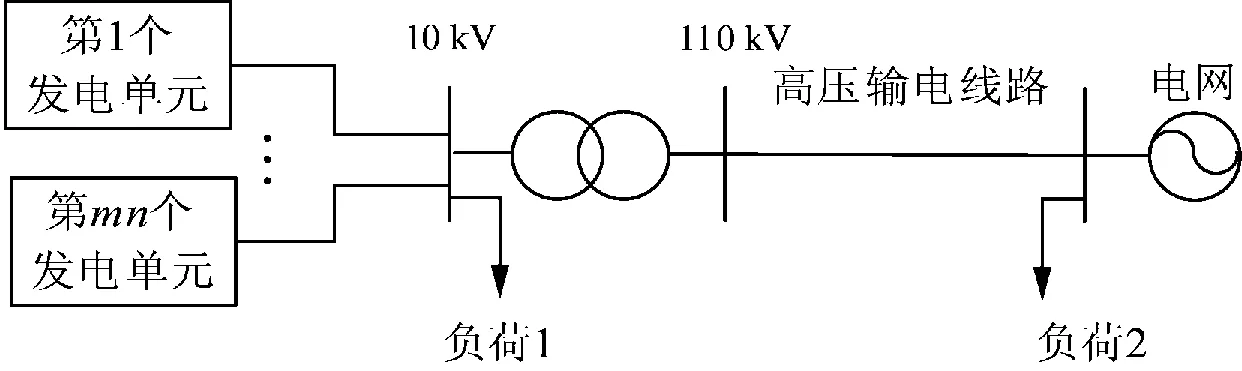
图7 忽略集电系统的大型光伏电站结构图

在建立了谐波传递网络之后，通过进行谐波潮流计算，可以得到网络中各个节点在各次谐波下的电压值。用某一点的各次谐波电压幅值除以该点的基波电压幅值，就可以得到在各次谐波下，该点的谐波电压相对于基波电压的放大倍数。由于谐波传递网络中的节点较多，本文仅选取主变压器低压侧节点，即各发电单元的公共连接点(point of common coupling，PCC)作为代表进行分析。网络中各个元件参数如表1所示。

表1 传递网络中各元件参数

Table 1 Parameters of every component in transfer network

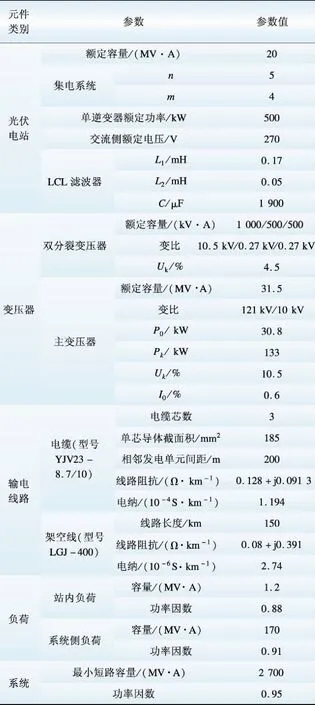
经计算，2种结构下PCC点谐波电压的放大情况如图8所示。从图8中可以看出，在忽略站内集电系统的电缆参数后，网络的谐振频率有所降低，谐振点的电压放大倍数也明显增大，其余各点的电压放大情况也有所改变。

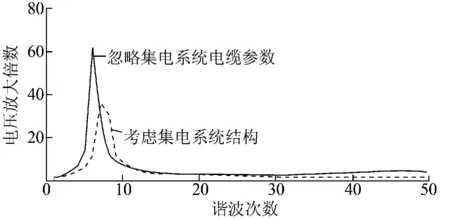
图8 PCC点各次谐波电压放大情况

2种结构下PCC点各次谐波的电压放大倍数如表2所示。从表2中数据可以看出，在考虑站内集电

表2 PCC点各次谐波电压放大倍数

Table 2 Harmonic voltage amplification properties of PCC

系统电缆参数的情况下，该网络在输入7次谐波电流时发生了谐振，当谐波次数小于7次时，电压放大倍数随输入谐波次数的增加呈上升趋势，随后逐渐下降，当谐波次数大于35次以后，谐波电压小于基波电压；在忽略站内集电系统电缆参数的情况下，网络在输入6次谐波电流时发生了谐振，当谐波次数小于6次时，电压放大倍数随输入谐波次数的增加呈上升趋势，随后逐渐下降，当谐波次数大于28次后，电压放大倍数的变化趋势与谐波次数没有明显的对应关系，但在该结构下，不论向网络注入几次谐波电流，PCC点的谐波电压幅值始终大于基波电压幅值。

由此可见，大型光伏电站中集电系统的电缆参数会对谐波分析结果造成一定影响，所以在进行谐波分析时应当考虑站内集电系统的电缆参数。

2.3 LCL滤波器的参数对谐波潮流计算结果的影响

考虑站内集电系统电缆参数的情况，在表1给定参数的基础上，单独调整LCL滤波器的参数L1、L2和C的值后，PCC点各次谐波电压的放大情况如图9—11所示。

图9 L1值对PCC点各次谐波电压放大情况的影响

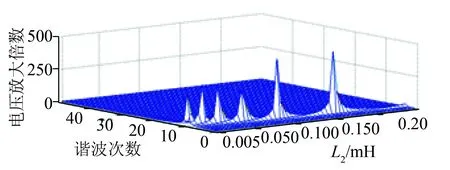
图10 L2值对PCC点各次谐波电压放大情况的影响

由图9—11可以看出，L1在图9所示范围内的变化没有对PCC点各次谐波电压的放大倍数产生明显的影响，但不排除对网络中其他节点谐波电压产生影响的可能；随着L2值的增大，PCC点的谐振频率逐渐减小，且谐振频率均在11次以下，谐振点的电压放大

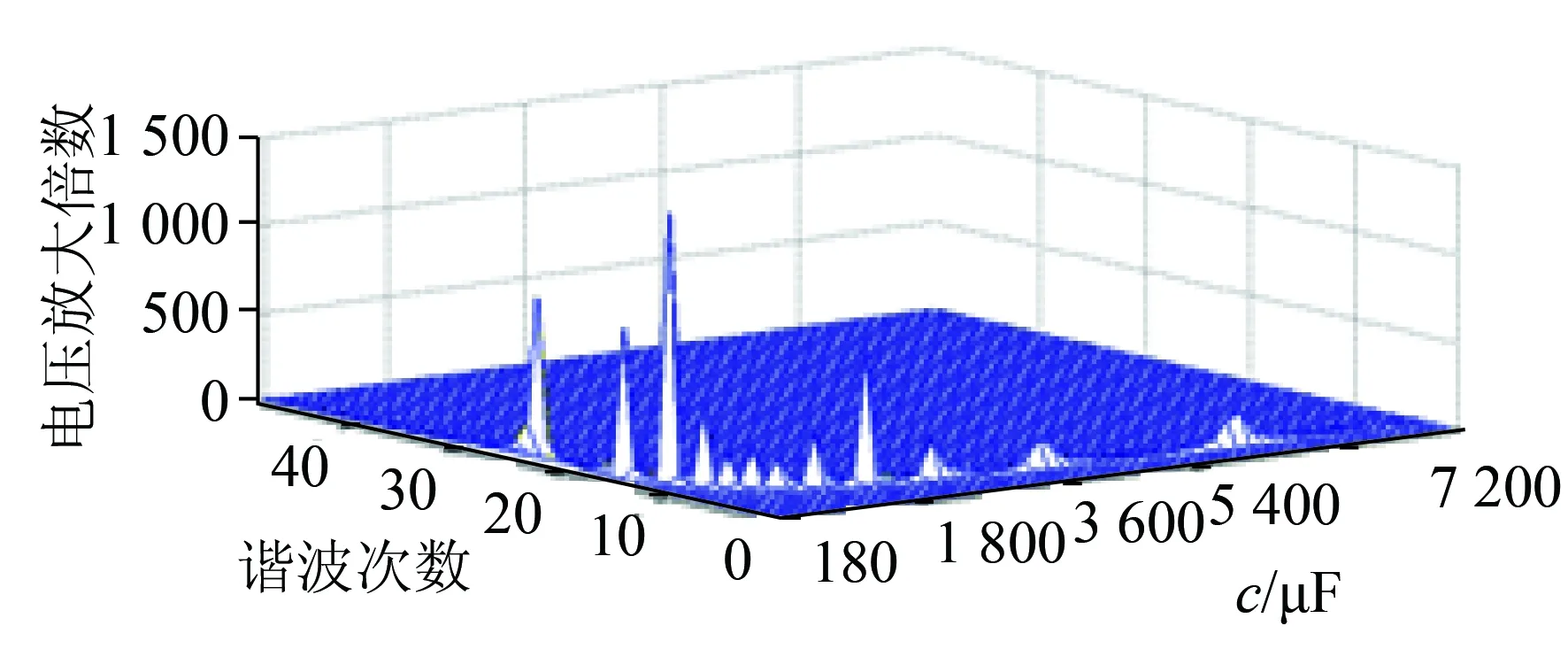
图11 C值对PCC点各次谐波电压放大情况的影响

倍数均在200倍以上；电容C对PCC点的各次谐波电压放大情况的影响与L2类似，随着C值的增大，PCC点电压的谐振频率逐渐减小，且谐振频率均在25次以下。但与L2相比，C值的变化更容易引起PCC点发生谐振。

2.4 电缆参数对谐波潮流计算结果的影响

考虑站内集电系统电缆参数的情况，在表1给定参数的基础上，单独调整单位长度电缆的阻抗和导纳的值后，PCC点各次谐波电压的放大情况如图12—13所示。

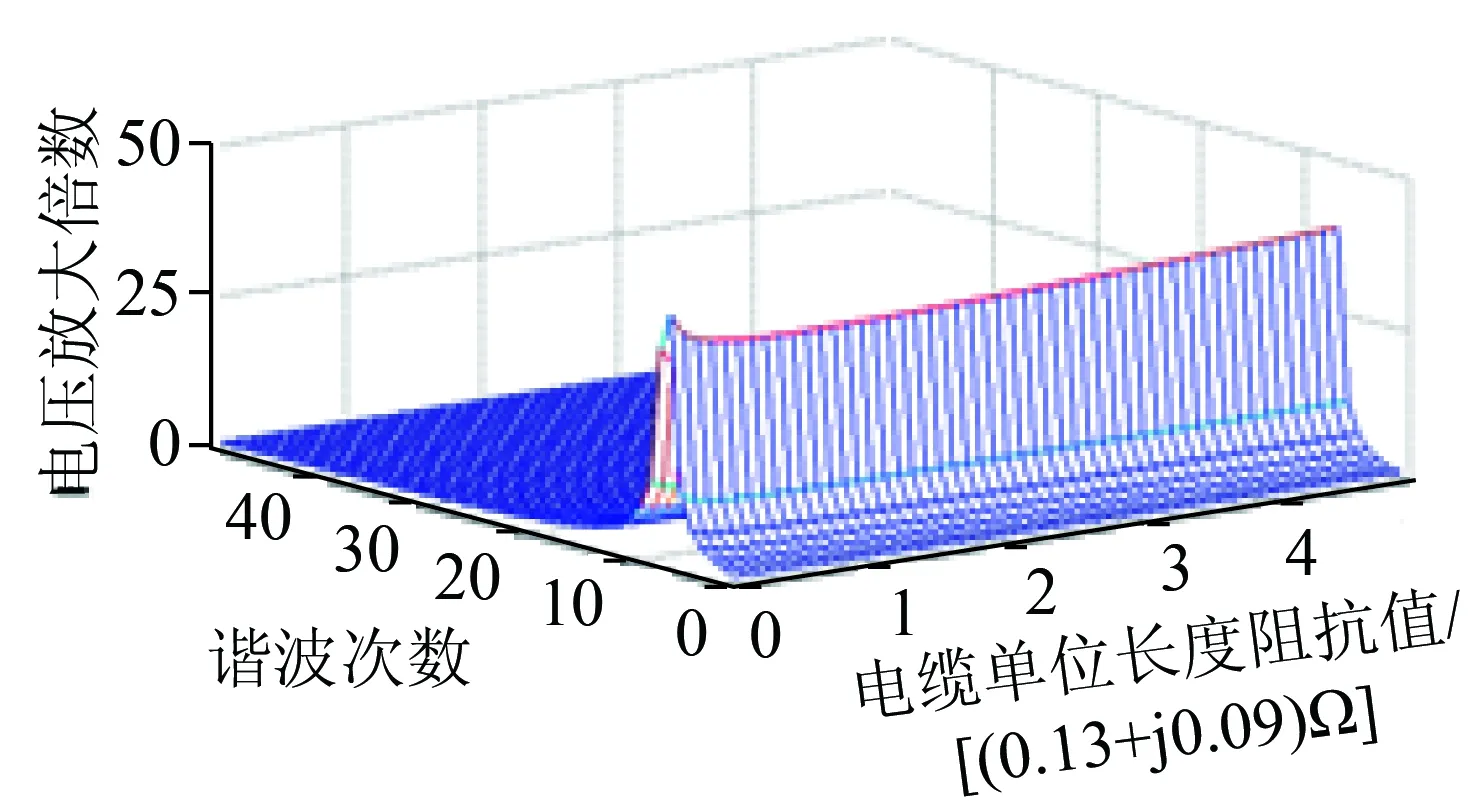
图12 电缆阻抗值对PCC点各次谐波电压放大情况的影响

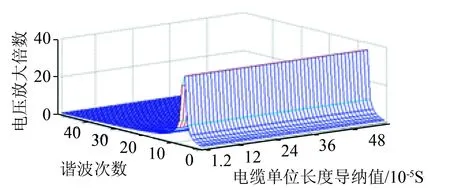
图13 电缆导纳值对PCC点各次谐波电压放大情况的影响

由图12—13可以看出，电缆阻抗值大小的改变对PCC点处的谐振频率几乎没有影响，但是随着电缆阻抗值的增大，PCC点在谐振频率下的电压放大倍数先减小后增大；电缆导纳值大小的改变对PCC点处的谐振频率也没有明显的影响，但是随着电缆导纳值的增大，PCC点在谐振频率下的电压放大倍数逐渐增大，但增大得比较缓慢。

由于在站内集电系统中，各发电单元之间的电缆线路长度短、电压等级低，所以电缆参数的改变对于PCC点各次谐波电压放大倍数的影响并不明显，但如果不考虑电压放大倍数，只从电压幅值的计算结果来看，电缆参数的改变对该点各次谐波电压幅值大小的影响较为明显。由此也可以说明，在对大型光伏电站进行谐波分析时，应当考虑电缆参数对于分析结果的影响。

3 结 论

(1)是否考虑光伏电站内部集电系统结构，PCC点的谐波电压放大特性存在明显差别。

(2)光伏逆变器的LCL滤波器参数对PCC点谐波电压放大特性有影响，其中L2与C值的改变对于谐波电压放大特性影响较为明显，L1的改变对PCC点的影响不明显，但是不排除其对电站内部节点存在影响。

(3)集电系统内部电缆线路参数对PCC点谐波电压放大特性有影响。由于各发电单元之间的电缆线路长度短、电压等级低，电缆参数的改变对于该点的谐波电压放大特性影响相对较小。

本文建立的考虑集电系统结构的谐波传递网络详细模型，对于光伏电站谐波电压放大机理和基本规律的说明是有意义的。

[1]国家电网公司.公司发布《促进新能源发展白皮书(2016)》[EB/OL]. (2016-03-15)[2016-05-24].http://www.sgcc.com.cn/shouye/tbxw/332320.shtml.

[2]赵争鸣，雷一，贺凡波，等.大容量并网光伏电站技术综述[J].电力系统自动化，2011，35(12)：101-107. ZHAO Zhengming，LEI Yi，HE Fanbo，et al. Overview of large-scale grid-connected photovoltaic power plants[J]. Automation of Electric Power Systems，2011，35(12)：101-107.

[3]丁明，王伟胜，王秀丽，等. 大规模光伏发电对电力系统影响综述[J]. 中国电机工程学报，2014，34(1)：1-14. DING Ming，WANG Weisheng，WANG Xiuli，et al. A review on the effect of large-scale PV generation on power systems[J]. Proceedings of the CSEE，2014，34(1)：1-14.

[4]李春来,王晶,杨立滨. 典型并网光伏电站的等值建模研究及应用[J]. 电力建设,2015, 36(8):114-121. LI Chunlai，WANG Jing，YANG Libin. Equivalent modeling research and application oftypical grid connected photovoltaic power station[J]. Electric Power Construction,2015, 36(8):114-121.

[5]张彦昌,石巍. 大型光伏电站集电线路电压等级选择[J]. 电力建设,2012, 33(11):7-10. ZHANG Yanchang, SHI Wei. Voltage level selection of collecting power lines for large-scale photovoltaic power station[J]. Electric Power Construction,2012, 33(11):7-10.

[6]董伟杰，白晓民，朱宁辉，等.间歇式电源并网环境下电能质量问题研究[J].电网技术，2013，37(5)：1265-1271. DONG Weijie，BAI Xiaomin，ZHU Ninghui，et al.Discussion on the power quality under grid-connection of intermittent power sources[J]. Power System Technology，2013，37(5)：1265-1271.

[7]VARMA R K，SALAMA M.Large-scale photovoltaic solar power integration in transmission and distribution networks[C]//2011 IEEE Power and Energy Society General Meeting. Detroit, Michigan, USA: IEEE, 2011: 1-4.

[8]SHIH F Y，CHEN D Y，WU Y P，et al. A procedure for designing EMI filters for AC line applications[J]. IEEE Transactions on Power Electronics，1996，11(1)：17-18.

[9]TURNER R，WALTON S，DUKE R.Stability and bandwidth implications of digitally controlled grid-connected parallel inverters[J].IEEE Transactions on Industrial Electronics，2010，57(11)：3685-3694.

[10]杨明，周林，张东霞，等.考虑电网阻抗影响的大型光伏电站并网稳定性分析[J].电工技术学报，2013，28(9)：214-223. YANG Ming，ZHOU Lin，ZHANG Dongxia，et al.Stability analysis of large-scale photovoltaic power plants for the effect of grid impedance[J].Transactions of China Electrotechnical Society，2013，28(9)：214-223.

[11]周林，张密，居秀丽，等. 电网阻抗对大型并网光伏系统稳定性影响分析[J]. 中国电机工程学报，2013，33(34)：34-41. ZHOU Lin，ZHANG Mi，JU Xiuli，et al. Stability analysis of large-scale photovoltaic plants due to grid impedances[J]. Proceedings of the CSEE，2013，33(34)：34-41.

[12]姚天亮,郑昕,杨德洲,等. 打捆并网方式下光伏电站无功补偿及谐波问题[J]. 电力建设,2011, 32(8):24-28. YAO Tianliang, ZHENG Xin, YANG Dezhou, et al. Dynamic reactive power compensation and harmonic problems of PV power plants under bundled grid-connection condition[J]. Electric Power Construction,2011, 32(8):24-28.

[13]周林,张密. 大型光伏电站谐振现象分析[J]. 电力自动化设备，2014，34(6)：8-14. ZHOU Lin，ZHANG Mi. Analysis of resonance phenomenon in large-scale photovoltaic power plant[J]. Electric Power Automation Equipment，2014，34(6)：8-14.

[14]谢宁，罗安，马伏军，等. 大型光伏电站与电网谐波交互影响[J]. 中国电机工程学报，2013，33(34)：9-16. XIE Ning，LUO An，MA Fujun，et al. Harmonic interaction between large-scale photovoltaic power stations and grid[J]. Proceedings of the CSEE，2013，33(34)：9-16.

[15]杜潇，周林，郭珂，等. 大型光伏电站静态电压稳定性分析[J]. 电网技术，2015，39(12)：3427-3434. DU Xiao，ZHOU Lin，GUO Ke，et al. Static voltage stability analysis of large-scale photovoltaic plants[J]. Power System Technology，2015，39(12)：3427-3434.

[16]谢宁，罗安，陈燕东，等. 大型光伏电站动态建模及谐波特性分析[J]. 中国电机工程学报，2013，33(36)：10-17. XIE Ning，LUO An，CHEN Yandong，et al. Dynamic modeling and characteristic analysis on harmonics of photovoltaic power stations[J]. Proceedings of the CSEE，2013，33(36)：10-17.

[17]芦晶晶. 电力系统谐波分析及程序开发[D]. 北京：中国电力科学研究院，2005. LU Jingjing. Power system harmonic analysis and software development[D]. Beijing: China Electric Power Research Institute，2005.

[18]WAKILEH G J. 电力系统谐波: 基本原理、分析方法和滤波器设计[M]. 徐政，译. 北京：机械工业出版社，2011: 10-11.

(编辑 景贺峰)

Harmonic Transfer Network Analysis of Large-Scale Photovoltaic Power Plant Electricity Energy Collection System

ZHU Yongqiang1, HAO Jiacheng1, TANG Qi1, YANG Huina1, LI Chunlai2

(1. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China; 2. Qinghai Province Key Laboratory of Grid-Connected Photovoltaic (PV) Technology, Xining 810000, China)

In large-scale photovoltaic (PV) power plant, the output power of every PV grid-connected inverter system is collected by electricity energy collection system and then is put into electricity grid. Previous studies have demonstrated that the harmonic problem may occur when PV inverters run in parallel even if all the PV inverters individually satisfy the standards. Considering the electricity energy collection system, this paper builds the model of harmonic transfer network for typical topological structure of large-scale grid-connected PV power plant. Using node matrix method, this paper calculates the harmonic power flow of a given calculation example in MATLAB and gets the fundamental and harmonic voltage amplitudes of every node. Taking the node of the low voltage side of main transformer as the study object, this paper compares the calculation result with that of neglecting the structure of the electricity energy collection system, whose results show that the voltage amplification property obviously changes. Finally, this paper analyzes the influence of the parameters of LCL filter and cable in the electricity energy collection system on the voltage amplification property of the harmonic transfer network.

large-scale photovoltaic power plant; electricity energy collection system; harmonic; transfer network

新能源电力系统国家重点实验室2016年自主研究课题项目(LAPS2016-14)

TM 615

A

1000-7229(2016)10-0122-08

10.3969/j.issn.1000-7229.2016.10.017

2016-06-14

朱永强(1975)，男，博士，副教授，主要研究方向为新能源发电与并网技术以及电力电子技术；

郝嘉诚(1992)，女，硕士研究生，主要研究方向为新能源发电与并网技术；

唐萁(1994)，男，硕士研究生，主要研究方向为新能源发电与并网技术；

杨慧娜(1972)，女，博士，讲师，主要研究方向为电工理论与新技术以及电力电子技术；

李春来(1980)，男，硕士，高级工程师，主要研究方向为新能源技术。