基于用户行为的家庭日负荷曲线模型

林顺富，黄娜娜, 赵伦加, 汤波, 李东东

(1. 上海电力学院电气工程学院，上海市 200090; 2. 国网湖北省电力公司孝感供电公司，湖北省孝感市 432000)

基于用户行为的家庭日负荷曲线模型

林顺富1，黄娜娜1, 赵伦加2, 汤波1, 李东东1

(1. 上海电力学院电气工程学院，上海市 200090; 2. 国网湖北省电力公司孝感供电公司，湖北省孝感市 432000)

居民用电所占比例逐渐提高，对配电网影响日益增大。有效的家庭日负荷曲线模型对需求侧管理及智能电网技术的发展至关重要。该文建立了基于用户行为的家庭日负荷曲线模型。基于测量数据，建立典型居民负荷电气学模型；基于统计调研数据，利用马尔科夫链蒙特卡洛(Markov chain Monte Carlo，MCMC)算法，引入概率函数表示居民人口、家用电器拥有情况等居民家庭特征的影响，建立居民负荷行为学模型。并采用自下向上的分层建模思路，结合电气学模型与行为学模型建立家庭日负荷曲线模型，同时搭建了仿真平台。所建模型具有系统性和通用性，仿真与实测对比分析验证了该文所提模型的可行性与准确性。

日负荷曲线；居民负荷；用户行为；马尔科夫链蒙特卡洛(MCMC)

0 引 言

目前，我国居民生活用电所占比例为总需求的12%，而美国为36%。随着社会经济的发展和人民生活水平的提高，居民用电仍有非常大的增长空间[1]。同时，家庭日负荷曲线的获取有利于推进智能电网、需求响应及电动汽车接入等技术的发展[2-4]。因此家庭日负荷曲线建模尤为必要。

居民负荷的建模方法主要分为2类：自下向上的负荷建模[5-8]和自上向下的负荷建模[9]。前者是以终端负荷为研究对象，基于每个电器的用电数据建立负荷模型，然后将单个电器的负荷模型组合以建立各层负荷模型；后者则以顶层系统为研究对象，基于系统测量数据建立负荷模型。相比之下，自下向上的建模方法所需数据量大，但模型精度高，并可得到系统各层的仿真数据。国外已有较多文献研究居民日负荷曲线的建模方法[10-13]。文献[10]基于测量和统计数据建立了较高时间分辨率的家庭日负荷曲线模型。文献[12-13]分别自下向上地建立了家庭日负荷曲线的统计模型和家用空调及热水器的负荷曲线模型。

居民负荷种类繁多、差异性较大，并且受居民生活习惯、家庭人口结构、环境条件等因素的影响，具有很大随机性[14-16]。[14]研究了27户居民家庭的用电模式，得出住宅类型、位置、家用电器种类、家庭人口等对居民用电有较大影响；年平均耗电量与住房面积密切相关。文献[15]将居民用电分解为电气系统和居民系统以研究家庭耗能特性。文献[16]提出一种基于用户行为的谐波评估方法，将概率函数引入谐波模型中，得到更为精确的居民负荷谐波模型。要精确评估居民负荷，需考虑上述因素的影响，即基于用户行为进行居民负荷建模。采用自下向上的建模方法可以兼顾居民行为对负荷曲线的影响，同时可以得到各层的负荷特征信息。

国内文献主要通过测试方法研究居民用电特征与地域、环境温度、社会经济、家庭收入等因素的关系[17-20]。文献[21]对中国6座城市近400栋楼宇进行了测试，研究电能消耗与地域、建筑类型、建筑规模的关系。总的来说，国内对居民负荷行为建模的研究较少，涉及到的研究主要与天气等自然环境相关，因此迫切需要进行居民行为对居民用电影响的研究工作。

本文建立基于用户行为的家庭日负荷曲线模型。基于测量数据，建立典型居民负荷的电气学模型；基于统计调研数据，利用马尔科夫链蒙特卡洛(Markov chain Monte Carlo，MCMC)算法，引入概率函数表示居民人口、家用电器拥有情况等居民家庭特征的影响，建立行为学模型。并采用自下向上的分层建模思路，结合电气学模型与行为学模型建立家庭日负荷曲线模型，同时搭建了仿真平台。所建模型具有系统性和通用性，适用于需求侧管理及智能电网研究，具有重要的理论意义和工程价值。

1 家庭日负荷曲线建模体系

用户行为决定家用电器运行状态，开启电器的负荷特性决定家庭日负荷曲线形态，居民负荷特征具有较大随机性。但居民的生活规律，如工作、用餐、作息时间等又具有相似一致性。因此结合用户行为构建自下向上的家庭日负荷曲线模型具有重要意义。

基于用户行为的家庭日负荷曲线建模体系如图1所示，采用自下向上的分层建模思路，即从单个电器出发分层建立日负荷曲线模型。基于实测数据，建立居民负荷电气学模型以反映居民负荷的用电特征；结合居民有效用电人数、电器日使用概率、电器平均使用时长构建居民负荷行为学模型。根据居民负荷电气学模型和行为学模型获得单个电器的日负荷曲线；进而将多个电器日负荷曲线叠加得到单户家庭日

图1 基于用户行为的家庭日负荷曲线建模体系

负荷曲线；同理得到多户家庭日负荷曲线。

2 居民负荷电气学模型

负荷电气学建模是建立负荷功率与电力系统变量(系统电压和频率)之间的数学关系，可反映负荷用电特征。多项式模型和指数模型是2种常用的负荷电气学模型[22]。多项式模型通常称之为ZIP模型，其数学表达式为

(1)

指数负荷模型表示负荷消耗功率与系统电压的指数关系：

(2)

式中：Ps表示供电电压为U时负荷的有功功率；P0表示负荷的额定有功功率；U0表示系统额定电压幅值；Zp、Ip、Pp为待求常数参数，幂指数α可由式(3)计算：

(3)

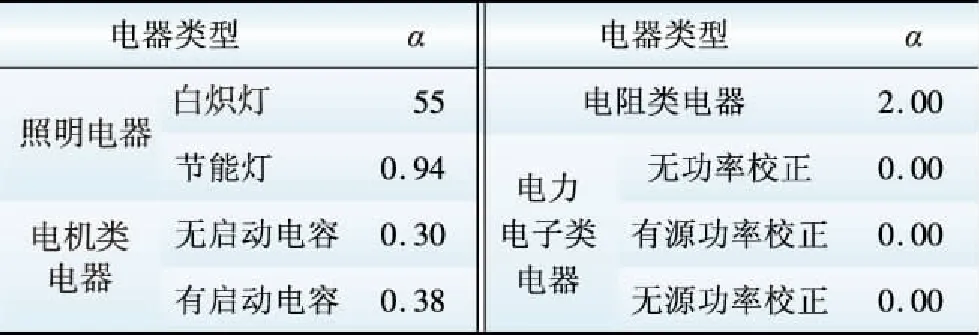
相比ZIP模型，指数负荷模型的应用更为广泛[23]。根据式(3)将典型家用电器的ZIP模型转化为指数负荷模型，模型参数如表1所示。表1将家用电器按用电特性分为以下4类：

(1)照明电器：白炽灯、节能灯等；

(2)电阻型电器：电热电器，如热水器、饮水机等；

(3)电机类电器：主要为白色家电，模型差别在于是否有启动电容；

(4)电力电子型电器：主要为电子消费产品，模型差别在于开关电源中功率因素校正电路类型。

表1 典型家用电器指数模型参数

Table 1 Exponential model parameters of

typical home appliances

3 居民负荷行为学模型

家用电器的使用并不是完全随机的，很大程度上受居民生活习惯的影响。本文基于统计调研数据，利用马尔科夫链蒙特卡洛方法建立居民负荷行为学模型。英国TUS(Time-Use Survey)数据库[22]和中国国家统计局的统计数据作为本文的基础数据库。英国TUS数据库对大量家庭进行调研，以10 min为统计精度，记录1天24 h活动日程，可以由此统计出1天内各时刻参与者的活动位置，得到住宅内的居民人数及其从事各种活动的概率。中国国家统计局统计了国内居民家庭各家用电器的拥有率和家庭人口比例。

3.1 MCMC方法

MCMC方法是一种特殊的蒙特卡洛方法，其将随机过程中的马尔科夫链应用到蒙特卡洛模拟中，抽样分布随模拟的进行而改变，从而实现动态模拟[24]。

马尔可夫链是具有马尔可夫性质的随机变量的一个数列。这些变量所有可能取值的集合，称为“状态空间”。Xt是t时刻的状态，则某一时刻tn的概率可由条件概率定义[25]：

FX(tn)|X(tn-1)=P[Xtn|Xtn-1]

(4)

离散序列Xt1,Xt2,…,Xtn是一个马尔科夫链。

马尔科夫链模型基于状态转移矩阵(即从某一状态转移到另一状态的概率)建立，其中一阶马尔科夫链表示一个随机序列的条件概率只与前一时刻的系统状态有关，而与之前的系统状态无关。其状态转移概率矩阵P如下所示：

(5)

3.2 居民有效用电人数

家用电器的使用与居民有效用电人数密切相关。居民有效用电人数即某一时刻处于非睡眠状态的人数。基于TUS数据库，利用MCMC方法仿真各时刻居民有效用电人数nt，如式(6)所示：

(6)

式中：w为0或1，分别表示周末和工作日；n表示家庭人口；Pi,j表示状态i到状态j的转移概率。

居民有效用电人数的状态转移，如图2所示。对于一个6口之家，居民有效用电人数nt包含6个状态，nt[0,1,2,3,4,5]，在时刻点tn，其由状态2到状态5的状态转移概率为P2,5(tn)。

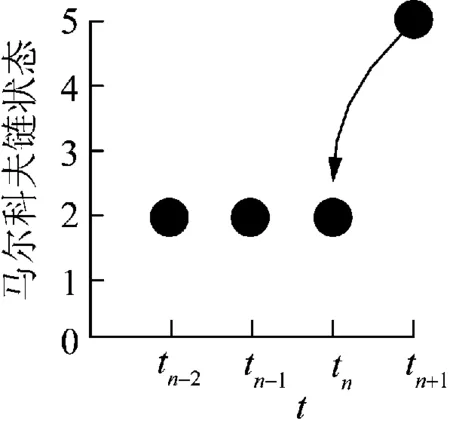
图2 tn时刻居民有效用电人数状态转移

各时刻居民有效用电人数仿真流程如图3所示。

图3 居民有效用电人数仿真流程图

(1)设定仿真初始条件w和n；

(2)基于统计数据，利用蒙特卡洛方法得到初始时刻居民有效用电人数，即确定马尔科夫链初始状态；

(3)计算马尔科夫链的状态转移概率，利用MCMC方法得到各时刻居民有效用电人数。状态转移概率由式(7)确定：

(7)式中：ni,j表示状态i转移到状态j的事件数；ni(t)表示t时刻状态i发生状态转移的数目；N表示状态总数。

人口数为4的单户家庭分别在工作日和周末的居民有效用电人数仿真结果，如图4所示。

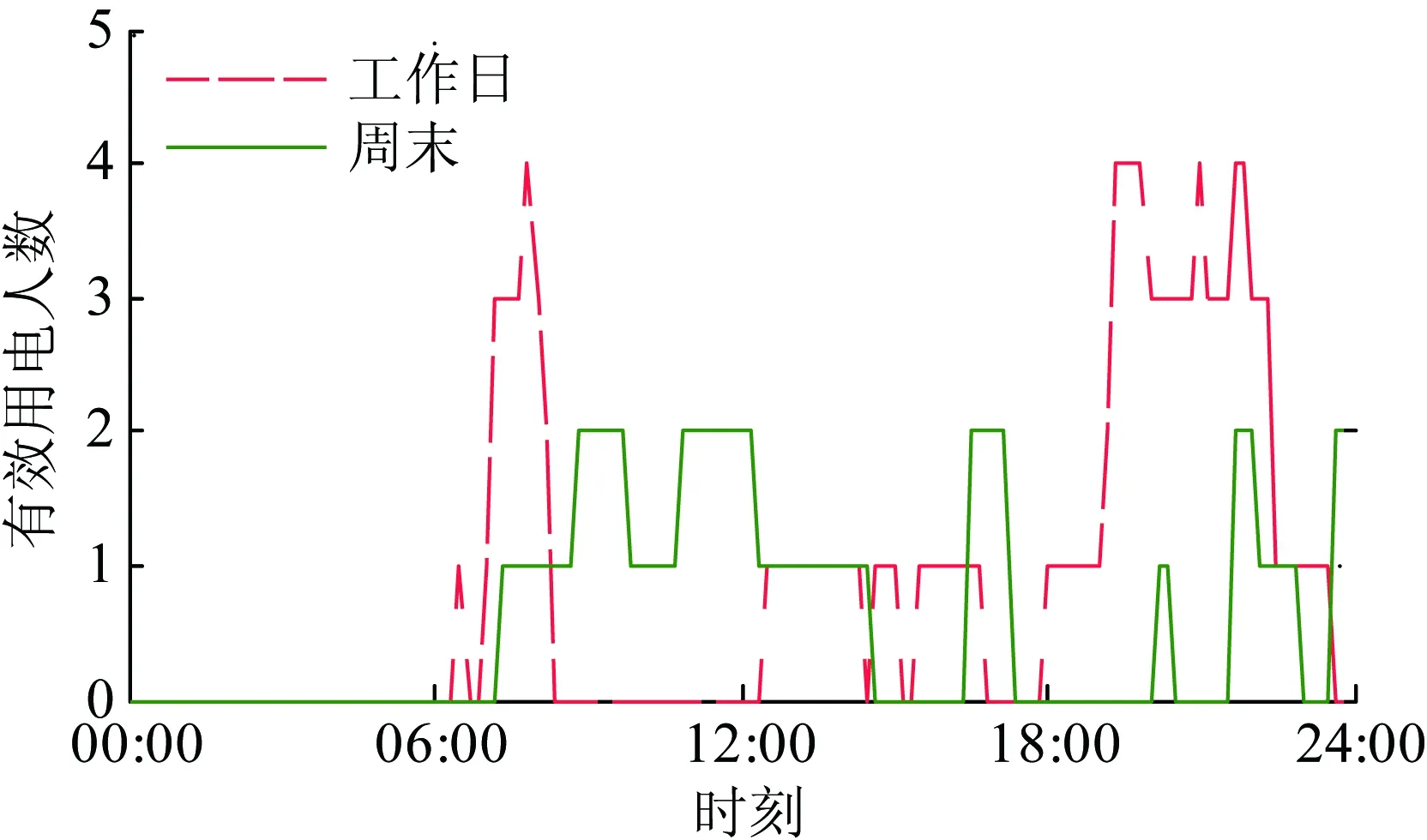
图4 居民有效用电人数

根据居民有效用电人数，建立相应的居民负荷日使用概率曲线，即居民负荷在1 d内不同时刻的开启概率。家用电器的日使用概率可由TUS数据获得。例如在时间段08:00—08:10，有效居民用电人数为1的用户数为2 082，此刻从事做饭活动的用户数为288，则做饭活动在此刻发生的概率是288/208 2=0.138。与做饭活动相关的电器使用概率为0.138。确定各时刻有效用电人数后，对电器日使用概率进行修正。根据图4可得到家用电器的日使用概率曲线，例如微波炉的日使用概率曲线如图5所示。

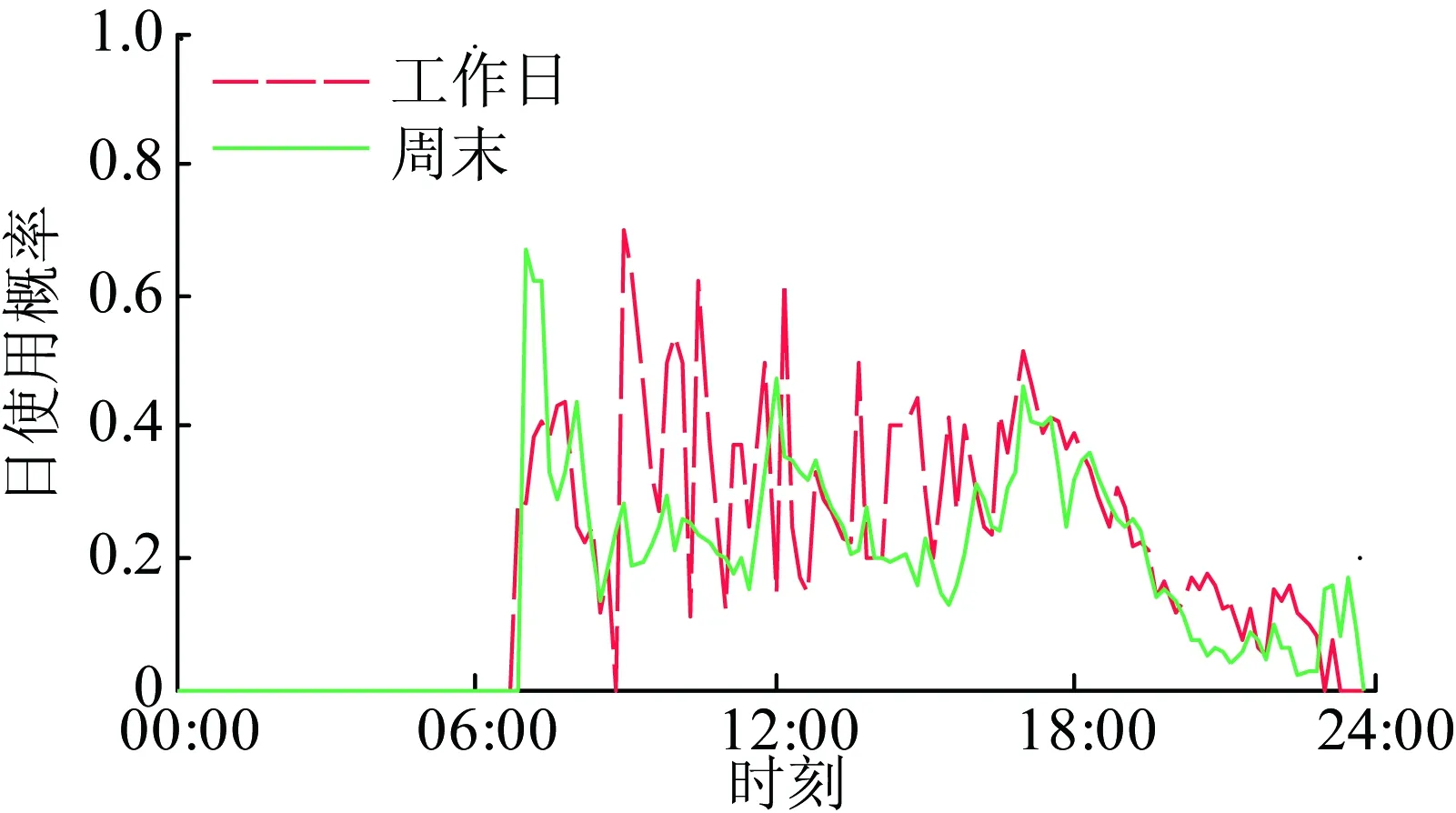
图5 微波炉日使用概率曲线

3.3 居民负荷平均使用时长

居民负荷平均使用时长可通过统计方式获取。加拿大住宅技术中心[26](Canadian center for housing technology，CCHT)和TUS都对典型居民负荷工作时长进行了调研。基于TUS数据库，典型居民负荷平均使用时长如表2所示。

表2 典型居民负荷平均使用时长

Table 2 Basic duration of typical home appliances

3.4 居民负荷开关模型

家用电器的开关状态决定居民负荷曲线特征，因此，研究居民负荷行为学模型的关键即建立居民负荷开关模型。居民负荷l在t时刻的开关状态Sl由式(8)确定：

(8)

式中：n(t)为t时刻居民有效用电人数；w表示工作日或周末；Pl(t)为居民负荷日使用概率。

结合居民有效用电人数和居民负荷平均使用时长，采用蒙特卡洛方法建立居民负荷的开关模型，仿真流程如图6所示，主要步骤如下所述。

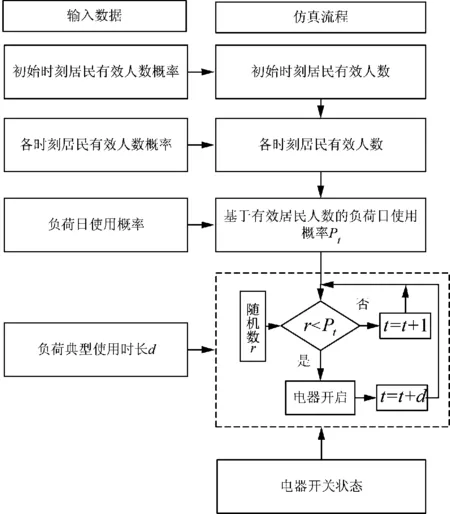
图6 居民负荷开关状态仿真流程图

(1)确定各时刻居民有效用电人数；

(2)结合居民有效用电人数曲线和不同家用电器的日使用概率统计数据，得到相应的各个家用电器的日使用概率曲线；

(3)基于家用电器日使用概率曲线，利用蒙特卡洛算法得到家用电器t时刻的开关状态；

(4)当负荷开启时，下一仿真时刻为(t+d)，d表示居民负荷平均使用时长；当负荷关闭时，下一仿真时刻为(t+1)，时间间隔为1 min，得到其各时刻开关状态。

典型家用电器开关状态的仿真结果如图7所示。由图7看出，洗衣机开启次数少，使用时间较短；热水器通常在晚上或早晨开启；微波炉开启次数较多，使用时间相对较短；电脑和电视机通常在晚上使用且持续时间长，电冰箱是间歇工作的，分为工作模式和待机模式。

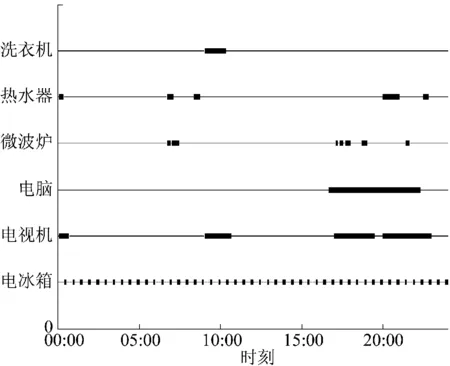
图7 典型家用电器开关状态

4 家庭日负荷曲线仿真

家庭的负荷特征由开启的家用电器共同决定。结合居民负荷电气学模型与行为学模型，可得到家庭日负荷曲线。

4.1 仿真结构

家庭日负荷曲线仿真结构如图8所示。图中左侧为家用电器日使用概率曲线，由统计调研获取。图中右侧每1层表示单户家庭日负荷曲线模型，每1户家庭设定2组参数：家用电器组合和有效用电人数。当家用电器开启时，根据电气学模型可得到其负荷特征。各时刻所有开启电器负荷曲线叠加即可获得单户家庭日负荷曲线。单户家庭和多户家庭的耗能分别由式(9)和(10)得出：

(9)

(10)

式中Ps,l为家用电器l的功率；Ph,i表示单户家庭功率。

图8 家庭日负荷曲线仿真结构图

4.2 家庭特征

4.2.1 家庭人口

根据2014年国家统计局统计数据，我国居民家庭平均人口数为2.97人，不同家庭人口占比如表3所示。

表3 不同家庭人口比例

Table 3 Population ratio of different families %

4.2.2 家用电器组合

家用电器种类繁多，依靠调研方法建立所有家庭的家用电器组合存在困难。基于国家统计局调研统计，家用电器拥有率如表4所示。研究大量家庭集体用电时，利用蒙特卡洛方法产生家用电器组合，可反映出一定的实际情况。

表4 家用电器拥有率

Table 4 Household appliances owning rate %

4.3 仿真分析

4.3.1 仿真结果

采用自下向上的分析方法，结合用户行为仿真得到人口数为3的单户家庭分别在工作日和周末的日负荷曲线如图9所示。由图9看出，与工作日相比，周末居民负荷的使用具有更大随机性；00:00—06:00通常为睡眠时间，开启状态的负荷少，耗电量低；用餐时刻及18:00—24:00为用电高峰时段。

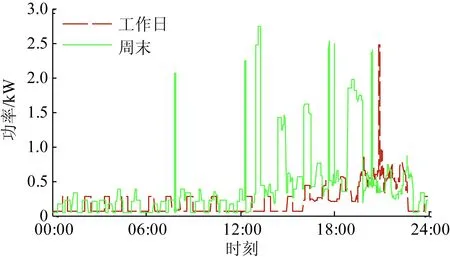
图9 单户家庭日功率仿真曲线

4.3.2 模型验证

对上海市某居民小区一2口之家的用电信息进行连续1个月的实测。其中某个典型工作日及周末的功率曲线如图10所示。由图9与图10对比可得，模型仿真功率曲线趋势与实测值基本一致。在夜间00:00—06:00阶段，仅冰箱等周期性负荷工作，功率曲线呈周期性。与工作日相比，周末的用电高峰时刻不仅发生在17:00以后，还通常发生在中午12：00左右。

图10 实测单户家庭日功率曲线

平均日负荷曲线通常用来作为选择配电系统元件容量的标准[11]。将30天内模型数据与实测数据平均值及方差作对比，以验证所建模型的有效性。图11是2口之家1个月内工作日及周末每h的功率均值及方差。由图11看出，模型结果与实测数据具有较好的相似性。

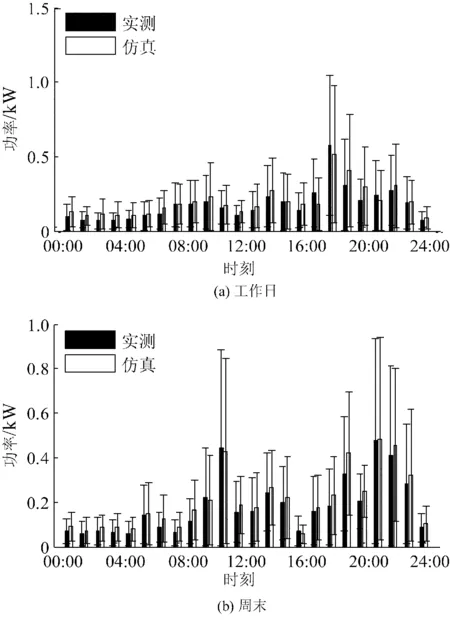
图11 单户家庭全天每h功率均值及方差的实测值与仿真值对比

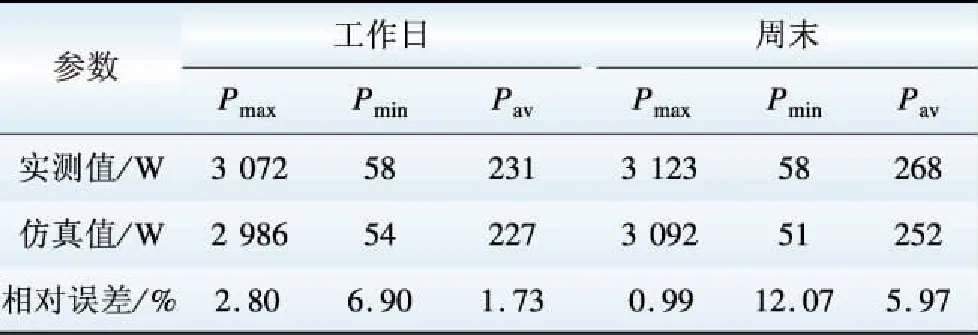
该户家庭1个月内分别在工作日和周末最大值、最小值和平均值的实测功率数据与模型仿真数据对比，如表5所示。由可得，模型仿真数据与实测数据在工作日和周末均具有较高的一致性，最大误差为12.07%。

表5 单户家庭1个月内最大、最小及平均值的仿真数据与实测对比

Table 5 Comparison of the maximum, minimum and average between simulated data and measured data of single household

单户家庭1个月内某周的工作日及周末的概率密度曲线如图12所示。由图12看出，实测值与仿真值的概率密度曲线具有良好的一致性。

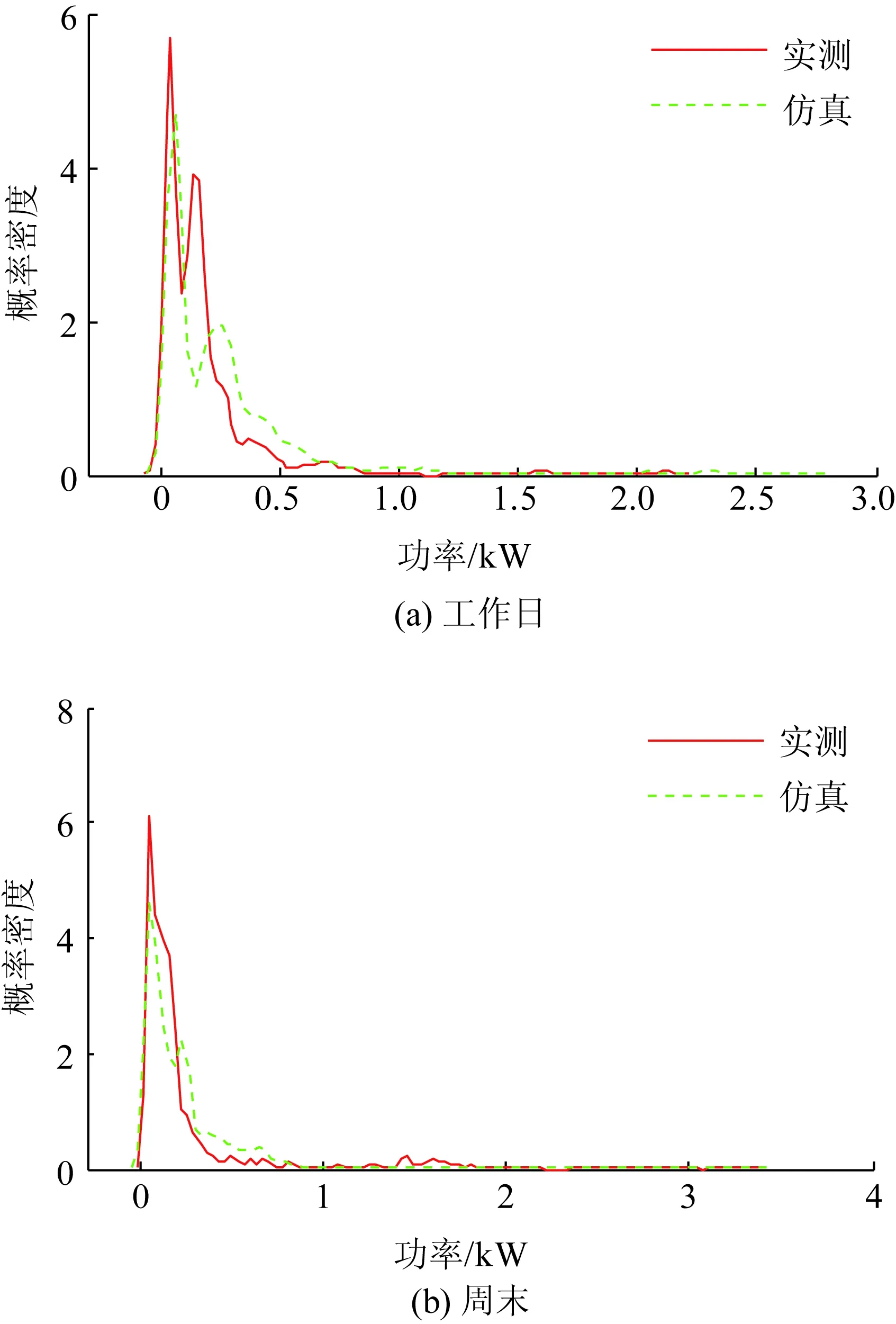
图12 单户家庭功率概率密度曲线实测与仿真对比

4.4 仿真平台建立

本文基于MATLAB软件，建立了居民家庭日负荷曲线仿真平台，仿真平台的整体结构框图如图13所示，其包含主界面和单个电器查看界面，如图14所示。主界面主要完成三大功能：(1)显示各时刻家庭有效用电人数仿真结果；(2)设置或随机产生居民家庭电器组合；(3)显示居民家庭日负荷曲线仿真结果。电器查看界面可以查看单个电器的使用情况。

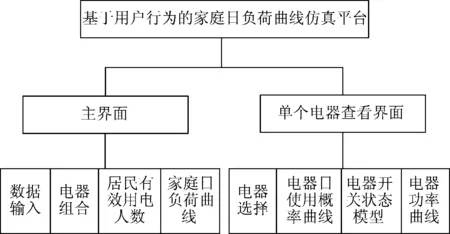
图13 基于用户行为的家庭日负荷曲线仿真平台

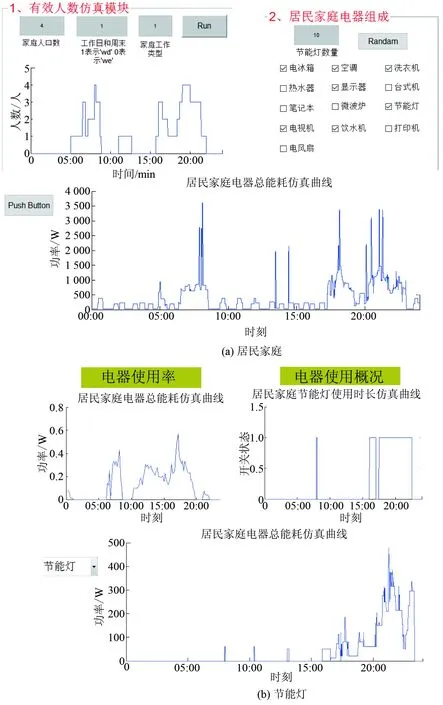
图14 居民家庭和节能灯日负荷曲线仿真平台界面图

5 结 论

本文基于统计调研数据，利用马尔科夫链蒙特卡洛算法，采用自下向上的建模方法，建立了基于居民行为的家庭日负荷曲线模型。该模型包含居民家庭特征的影响，引入负荷日使用概率曲线及居民有效用电人数曲线，结合居民负荷平均使用时长得到负荷开关状态，即居民负荷的行为学模型。基于实测数据，建立了典型居民负荷的电气学模型。将行为学模型和电气学模型相结合，仿真得到单户家庭的日负荷曲线，并将单户家庭叠加得到多户家庭的日负荷曲线，仿真与实测结果具有良好的一致性，证实模型有效。该模型可应用于需求侧管理、智能电网及配电网动态研究，具有重要工程价值。

[1]王葵，李建超，潘贞存，等. 居民谐波调查及仿真分析[J]. 电力系统保护与控制，2008，36(22)：88-103. WANG Kui, LI Jianchao, PAN Zhencun, et al. Harmonic investigation of resident customer and simulation analysis [J]. Power System Protection and Control, 2008, 36(22): 88-103.

[2]COLLIN A J，TSAGARAKIS G，KIPRAKIS A E，et al. Development of low-voltage load models for the residential load sector[J]. IEEE Transactions on Power Systems，2014，29(5): 2180-2188.

[3]黄海新, 邓丽, 文峰，等. 基于实时电价的用户用电响应行为研究[J]. 电力建设，2016, 37(2)：63-68. HUANG Haixin, DENG Li, WEN Feng, et al. Customer response behavior based on real-time pricing[J]. Electric Power Construction, 2016, 37(2)：63-68.

[4]和敬涵, 谢毓毓, 叶豪东, 等. 电动汽车充电模式对主动配电网的影响[J]. 电力建设，2015, 36(1): 98-102. HE Jinghan, XIE Yuyu, YE Haodong, et al. Influence of electric vehicles charging modes on active network distribution [J]. Electric Power Construction, 2015, 36(1): 98-102.

[5]SWAN L G， UGURSAL V I. Modeling of end-use energy consumption in the residential sector: a review of modeling techniques [J]. Renewable and Sustainable Energy Reviews, 2009, 13(8): 1819-1835.

[6]CHEN Y，CHU C，TSAO S，et al. Detecting users’ behaviors based on nonintrusive load monitoring technology [C]//10th IEEE International Conference on Networking，Sensing and Control (ICNSC). Evry: ICNSC，2013：804-809.

[7]DING T，LIANG H，XU W. An analytical method for probabilistic modeling of the steady-state behavior of secondary residential system [J]. IEEE Transactions on Smart Grid，2016, PP(99): 1-10.

[8]CHUAN L，UKIL A. Modeling and validation of electrical load profiling in residential buildings in Singapore [J]. IEEE Transactions on Power Systems，2015，30(5): 2800-2809.

[9]JARDINI J A，TAHAN C M V，GOUVEA M R，et al. Daily load profiles for residential，commercial and industrial low voltage consumers[J]. IEEE Transactions on Power Delivery, 2000，15(1)：375-380.

[10]MARSZAL-POMIANOWSKA A, HEISELBERG P, LARSEN O K. Household electricity demand profiles -A high-resolution load model to facilitate modelling of energy flexible buildings [J]. Energy，2016, 103: 487-501.

[11]JAMBAGI A, KRAMER M, CHENG V. Residential electricity demand modelling: Activity based modelling for a model with high time and spatial resolution[C]//2015 3rd International Renewable and Sustainable Energy Conference (IRSEC). Marrakech: IEEE, 2015：1-6.

[13]FISCHER D, WOLF T, SCHERER J, et al. A stochastic bottom-up model for space heating and domestic hot waterload profiles for German households[J]. Energy and Buildings, 2016,124:120-128.

[14]YOHANIS Y G，MONDOL J D，WRIGHT A，et al. Real-life energy use in the UK: How occupancy and dwelling characteristics affect domestic electricity use [J]. Energy and Buildings， 2008，40(6): 1053-1059.

[15]CHIOU Y-S. An occupant-driven integrative household system for residential building energy simulation[D]. Pittsburgh，Pennsylvania：Carnegie Mellon University，2009.

[16]SALLES D，JIANG C，XU W，et al. Assessing the collective harmonic impact of modern residential loads—Part I: methodology[J]. IEEE Transactions on Power Delivery，2012，27(4)：1937-1946.

[17]沈勇，杨荥，俞国勤，等. 上海地区居民用电的影响因素和需求预测模[J]. 华东电力，2012，40(10)：1763-1766. SHEN Yong, YANG Ying, YU Guoqin, et al. Influencing factors and demand forecast model for residential electricity consumption in Shanghai[J]. East China Electric Power, 2012，40(10)：1763-1766.

[18]周晖，钮文洁，纪洪. 各种因素影响下的居民夏季用电状况分析[J]. 华北电力技术, 2003(3)：12-21.

[19]陈晶，张真. 居民生活用电特征与影响机理[J]. 统计研究, 2015, 32(5): 70-75. CHEN Jing, ZHANG Zhen. Characteristics and impact mechanism of residential electricity consumption[J]. Statistical Research, 2015, 32(5): 70-75.

[20]曹磊，祖蓓. 夏季温湿指数与气象敏感电力负荷的研究[J]. 现代电力, 2011, 28(5): 41-45. CAO Lei, ZU Bei. Research on summer temperature humidity index and weather sensitive electric load[J]. Modern Electric Power, 2011, 28(5): 41-45.

[21]XU P，HUANG J，SHEN P，et al. Commercial building energy use in six cities in Southern China[J]. Energy Policy，2013，53(1)，76-89.

[22]MILANOVIC J V，YAMASHITA K，MARTNEZ VILLANUEVA S，et al. International industry practice on power system load modeling[J]. IEEE Transactions on Power Systems, 2013，28(3)：3038-3046.

[23]许淑敏. 电力负荷模型结构的研究[D]. 北京: 华北电力大学, 2006. XU Shumin. The study of power system load model structure [D]. Beijing: North China Electric Power University, 2006.

[24]石文辉, 别朝红, 王锡凡. 大型电力系统可靠性评估中的马尔可夫链蒙特卡洛方法[J]. 中国电机工程学报，2008, 28(4): 9-15. SHI Wenhui, BIE Chaohong, WANG Xifan. Applications of Markov chain Monte Carlo in large-scale system reliability evaluation [J]. Proceedings of the CSEE, 2008, 28(4): 9-15.

[25]王勇, 韩学山, 丁颖，等，基于马尔科夫链的电力系统运行可靠性快速评估[J]. 电网技术, 2013, 37(2)：405-410. WANG Yong, HAN Xueshan, DING Ying, et al. Markov chain-based rapid assessment on operational reliability of power grid[J]. Power System Technology, 2013, 37(2)：405-410.

[26]BELL M, SWINTON M，ENTCHEV E, et al. Development of micro combined heat and power technology assessment capability at the Canadian centre for housing technology[R]. Ottawa, ON, Canada, Tech. Rep. B-6010, 2003.

(编辑 张媛媛)

Domestic Daily Load Curve Modeling Based on User Behavior

LIN Shunfu1, HUANG Nana1, ZHAO Lunjia2, TANG Bo1, LI Dongdong1

(1. College of Electrical Engineering, Shanghai University of Electric Power, Shanghai 200090, China; 2. Xiaogan Power Supply Bureau, State Grid Hubei Electric Power Company, Xiaogan 432000, Hubei Province, China)

With the proportion of residential power consumption growing gradually, the residential loads have the increasing influence on the distribution network. The effective modeling of domestic daily load curve is critical for the development of demand side management and smart grid. This paper constructs the model of domestic daily load curve based on user behavior. We construct the electrical models of typical residential loads based on the tested data. And based on the statistic research data, we adopt Markov chain Monte Carlo (MCMC) method to construct the behavioral models of residential loads which introduces probability functions to represent the influence of resident household characteristics such as resident population and household appliances owned. Then, we adopt a bottom-up modeling method to construct the model of domestic daily load curve and the simulation platform with combining electrical model and behavioral model. The proposed model is universal and systematic, whose feasibility and accuracy are validated through the compared analysis between simulations and measurement.

daily load curve; residential load; user behavior; Markov chain Monte Carlo (MCMC)

国家自然科学基金项目(51207088); 国家电网公司科技项目(SGRI-DL-71-14-004)；上海市科委科创项目(14DZ1201602)；上海绿色能源并网工程技术研究中心项目(13DZ2251900)；上海市教委曙光计划项目(15SG50)

TM 73

A

1000-7229(2016)10-0114-08

10.3969/j.issn.1000-7229.2016.10.016

2016-07-25

林顺富(1983)，男，教授，从事电能质量及智能电网用户端技术的研究工作；

黄娜娜(1992)，女，硕士研究生，从事电能质量及智能电网用户端技术的研究工作。

Project supported by the National Natural Science Foundation of China(51207088)