基于起振波形数据与相干谱的低频振荡类型识别方法

王丽馨，蔡国伟，杨德友，孙正龙

(东北电力大学电气工程学院，吉林省吉林市 132012)

基于起振波形数据与相干谱的低频振荡类型识别方法

王丽馨，蔡国伟，杨德友，孙正龙

(东北电力大学电气工程学院，吉林省吉林市 132012)

根据激励的不同，电力系统有功功率低频振荡主要表现为强迫功率振荡和负阻尼振荡。2种振荡表现形式相似，但控制方法不同。在深入分析电力系统有功功率振荡解析表达式的基础上，对2种振荡的外在表征及区别进行总结和概括，进而提出了基于相干谱法的低频振荡类型识别方法。该方法首先需要从安装在不同发电机组的广域相量测量系统(wide area measurement system，WAMS)中获取2组含有噪声的振荡初期数据，利用相干谱理论计算2组数据的幅值平方相干函数值，通过对幅值平方相干函数值的量化比较实现低频振荡类型的识别。4机2区域系统仿真计算与分析，验证了所提识别方法的可行性及有效性。

电力系统；低频振荡；强迫功率振荡；负阻尼振荡；相干谱法

0 引 言

随着我国互联电网规模的不断扩大，电力系统有功功率低频振荡已成为影响电力系统安全稳定运行的重要突出问题[1-3]。

电力系统常见的低频振荡分为2类：负阻尼振荡和强迫功率振荡。其中，理论比较完善，实际工程应用最多的是负阻尼理论[4]。近几年，强迫振荡机理很好地解释了一些负阻尼机理无法解释的问题，越来越受到国内外学者广泛认同与关注。强迫振荡机理是基于共振机理提出的[5]。该机理认为发电机机械功率、励磁电压或者负荷的周期性扰动均能引起系统的强迫振荡。强迫功率振荡是由扰动源主导的，切除扰动源后，振荡迅速消失[6]。强迫功率振荡和负阻尼振荡二者的产生机理和控制策略均不相同，而二者表现形式很接近，单从振荡现象难以区分。因此，正确有效地识别振荡类型，对于抑制电网低频振荡具有重要意义。

国内外学者对于低频振荡尤其是强迫功率振荡的扰动源性质[7-8]和扰动源定位[9-11]做了大量研究，而对于低频振荡类型判别的问题研究较少，成果尚不多见。文献[12]依据起振阶段功率最大值的一次差分和二次差分的符号来区分2种振荡。文献[13]依据负阻尼振荡和强迫功率振荡的端口供给能量中的趋势分量变化规律的不同来判别振荡类型。文献[14]通过提取主振荡信号，对其进行包络线拟合，依据拟合误差判别振荡类型。但是，现有文献所提出的振荡类型识别方法在低噪声环境下普遍适用，对于强噪声环境下，现有振荡类型识别方法可能无法达到理想的效果。

本文提出一种在低信噪比环境下，基于振荡初期阶段波形和相干谱法的电力系统振荡类型识别法。首先，采集得到2组发电机出口有功功率，去掉趋势分量后，将信号通过低通和高通滤波器处理，计算幅值平方相干函数。最后，依据相干谱中峰值的大小识别振荡类型。

1 电力系统功率振荡基本特征

对于单机无穷大系统，发电机采用经典二阶模型，则发电机转子运动方程[5]为

(1)

式中：Δδ为发电机转子角偏移；Δω为发电机转子角速度偏移；ω0为稳态运行下的转子角速度；TJ为机组惯性时间常数；ΔPe为电气输出功率变化量；ΔPm为机械功率变化量；D为发电机阻尼系数。

将转子运动方程在工作点附近线性化，可得到二阶常系数非齐次微分方程为

(2)

式中Ks为发电机同步转矩系数。

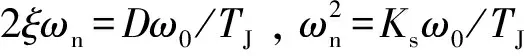
式(1)解的形式包含通解和特解2个部分，通解即对应的齐次方程的解，特解则与机械功率变化量ΔPm有关。假设ΔPm=F0sinωt，则其通解形式为

Δδ1(t)=A0e-ξωntsin(ωdt+φ0)

(3)

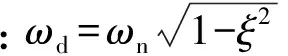
特解形式为

Δδ2(t)=Bsin(ωt-φ)

(4)

其中：

(5)

式中：ω为外施扰动频率。因此，系统的总响应为

Δδ(t)=Δδ1(t)+Δδ2(t)

(6)

可知，强迫功率振荡扰动的初始阶段由自由振荡和纯强迫振荡组成，当系统阻尼为正时，与阻尼有关的自由振荡衰减以后，余下的特解表现为纯强迫振荡，即等幅振荡。

对于自由振荡的系统，一般忽略原动机的功率变化，转子运动方程转变为二阶常系数微分方程：

(7)

式(7)即为应用负阻尼机理分析电力系统低频振荡时的转子运动方程，其解的形式如式(3)所示，而对于多机系统，自由振荡解的形式为

Δδ1(t)=A0e-ξ0ωntsin(ωdt+φ0)+A1e-ξ1ωnt×

sin(ωdt+φ1)+…+Ane-ξnωntsin(ωdt+φn)

(8)

A0e-ξωnt为随时间变化的振幅，如果系统为负阻尼，则ξ为负数，系统受到扰动后将发生增幅振荡；如果系统阻尼接近于0，则ξ为0，受扰后系统将发生等幅振荡；如果系统为正阻尼，则ξ为正数，受扰后振荡将逐渐衰减。

电力系统发生自由振荡时，振荡初期是多种振荡模式并存的，既存在正阻尼振荡模式的衰减，又含有负阻尼振荡模式的增幅振荡。随着正阻尼振荡模式的衰减，进入振荡后期，负阻尼振荡模式逐渐成为系统的主导振荡模式，其对应频率成为系统的主导振荡频率，而扰动初始阶段，该主导振荡模式并不突显。对于2组振荡初期时域响应数据，经拉普拉斯变换后的频域响应之间不能彼此线性表示。而对于强迫功率振荡，是由同一个外施扰动源引发的振荡，系统各状态变量均表现为相同的振荡形式，即迅速起振，之后为等幅振荡，2组时域响应信号对应的频域响应之间可以近似彼此线性表示。

通过采集振荡初期数据，判断2组时域响应信号对应的频域响应之间能否近似线性表示，识别电力系统振荡类型。

2 相干谱分析法

相干技术是频域上的一种振动信号源识别技术，已广泛应用于地震信号分析，汽车振动分析及土木工程等领域，在信号分析方面具有重要作用[15]。

2组时间信号(如xt和yt)在频率f处的相干谱(又被称作是“幅值平方相干函数”)定义如下：

(9)

式中：Pxx(f)和Pyy(f)分别是xt和yt的功率谱密度；Pxy(f)是互功率谱密度。

Cxy(f)的大小反映了在频率f处，xt和yt的线性相关性，可以被认为是在频率f处，yt可以被xt线性表示出来的百分率。例如，xt是频率为fx正弦函数，而yt是频率为fy的另外一个正弦函数，则式(10)成立：

(10)

此外，Cxy(f)一般为实数，满足：

0≤Cxy(f)≤1 , ∀f∈R

(11)

本文利用基于快速傅里叶变换的Welch法计算互功率谱密度及自功率谱密度，窗函数采用汉宁窗(Hanning)，各窗数据段之间重叠率为50%。

通过对相干谱分析法分析，彼此可以近似线性表示的2个信号，在相干谱的某一频率处会出现峰值。数学手段解释为，在稳定平衡点处，用ARMA模型表示系统[16]：

(12)

(13)

式中：X1(s)和X2(s)分别为系统的2个不同时域响应的拉普拉斯变换；U(s)为扰动源的拉普拉斯变换；N1(s)和N2(s)分别为2组随机噪声信号的拉普拉斯变换。

对于由扰动源U(s)引起的具有主导频率的系统响应X1(s)和X2(s)，忽略随机噪声N1(s)和N2(s)的情况下，可以近似表示为

(14)

换句话说，系统的2组响应信号在主导频率处可以近似线性表示。因此，在主导频率处相干谱幅值接近于1。同时，由于噪声信号N1(s)和N2(s)不相关，故在该频率处相干谱峰值接近于0。

3 基于相干谱的电力系统低频振荡类型识别

2种振荡的表现形式相似，尤其在较高噪声环境下，更加难以区分。而相干谱分析法具有在噪声环境下辨识出周期性信号的优势，并且在相干谱主导振荡频率处出现较为明显的峰值，故可以对2种振荡进行有效的区分。

强迫功率振荡为同一个外施扰动源激励引发的振荡，起振较快，2组时域响应信号经拉普拉斯变换后的频域响应之间可以近似线性表示，从而2组响应信号的幅值平方相干函数会有一个较大值，即相干谱中会有一个较大的峰值。而负阻尼振荡是由系统故障等激发出的振荡，是系统固有属性，与外施扰动源无关。振荡初期为多个振荡模式并存的，随着正阻尼振荡模式的衰减，进入振荡后期，负阻尼振荡模式成为系统主导振荡模式，而扰动初始阶段，该主导振荡模式并不突显。因此，利用振荡初期数据计算幅值平方相干函数的结果较小，在相干谱图中不会出现明显的峰值。通过相干谱峰值阈值的合理设置，从而将2种振荡加以区分。

广域测量系统(wide area measurement system，WAMS)借助于高速通信网络的传输功能，将相量测量单元采集的广域数据上传到数据处理中心。随着WAMS的广泛建设和应用，为电力系统低频振荡分析提供了有效的技术手段。

相对于发电机功角或转子角速度，有功功率较容易获得。因此，选取WAMS采集得到的2组发电机出口有功功率进行相干谱分析。在计算信号相干性之前，需要对2组信号进行前期处理。首先，对输入信号进行去趋势分量处理，去掉采样信号中的线性趋势分量。由于主要关心电力系统低频振荡模式，即0.1～2.5 Hz，因此将信号通过截止频率为2.5 Hz的有限脉冲反应滤波器，去掉高频部分，再通过截止频率为0.1 Hz的有限脉冲反应滤波器，去掉低频部分。采样频率为5 Hz。然后，分别计算2组信号自功率谱和互功率谱，最后计算得到2组信号的相干谱。振荡类型识别流程如图1所示。图1中h为相干谱的峰值，η为相干谱峰值阈值。通过查阅文献及大量仿真，本文相干谱分析阈值η给定0.7[16]。当相干谱中最大峰值小于设定阈值时，则判断为负阻尼振荡，当峰值大于设定阈值时，判断为强迫功率振荡。将系统振荡类型识别结果反馈给控制中心，以便于调度员采取有针对性的平息振荡方法。

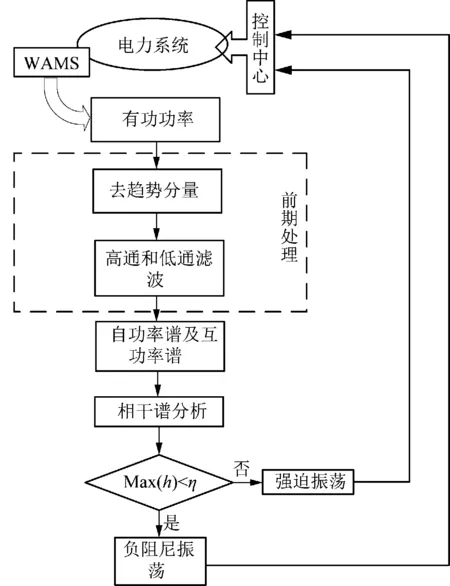
图1 基于相干谱的振荡类型识别流程图

4 仿真分析

4.1 4机2区域系统计算分析

IEEE 4机2区域系统结构如图2所示，数据参见文献[4]。

图2 4机2区域系统接线

首先利用小干扰稳定分析算法提取基础运行方式下系统机电振荡模式，计算共得到1个区域间振荡模式，2个本地振荡模式，结果如表1所示。

表1 4机2区域系统特征值分析结果

Table 1 Eigenvalue analysis results of four-generators two-area system

为了模拟实际系统2种常见低频振荡：负阻尼振荡和强迫功率振荡，本文分别设置2种扰动形式：(1)在母线3设置一维持0.05 s的三相短路接地故障，激发系统0.626 2 Hz的负阻尼区间振荡；(2)在发电机1励磁系统中施加持续周期性扰动F0sinωt=0.005sin(2πf)(pu)，f=0.62 Hz，扰动持续时间0～25 s。

图3为低噪声环境下，强迫振荡和负阻尼振荡时，发电机1出口有功功率波形图。图4为强噪声环境下2种振荡对应的发电机1有功功率波形，信噪比约为20 dB。发电机3的情况与发电机1类似，此处不再赘述。

图3 无噪声下2种振荡波形对比

图4 含噪声的2种振荡波形对比

由图4可以看出，噪声环境下，扰动前期，强迫振荡与负阻尼振荡外在表现形式很相似，仅从时域响应信号外部表现很难区分。因此，利用本文提出的相干谱振荡类型识别方法，及时识别出低频振荡类型，为调度运行人员采取紧急控制措施提供依据。

首先，选取同一个振荡区间发电机1和2有功功率振荡波形起振阶段连续振荡的7个周波的数据作为分析信号。2台发电机出口有功功率分别经过去趋势分量和高通、低通滤波后，进行相干性计算分析，相干谱如图5所示。然后，选取位于不同振荡区间的发电机1和发电机3的出口有功功率为基础数据，进行相干谱计算，分析结果如图6所示。

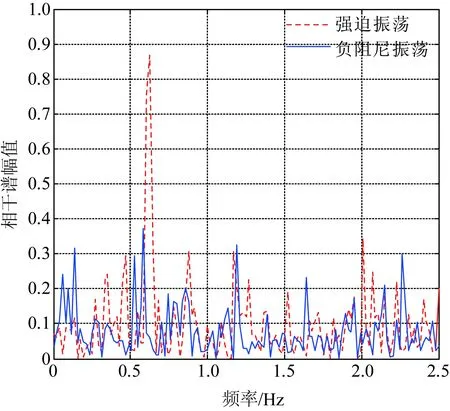
图5 基于发电机1和2有功功率的相干谱分析图

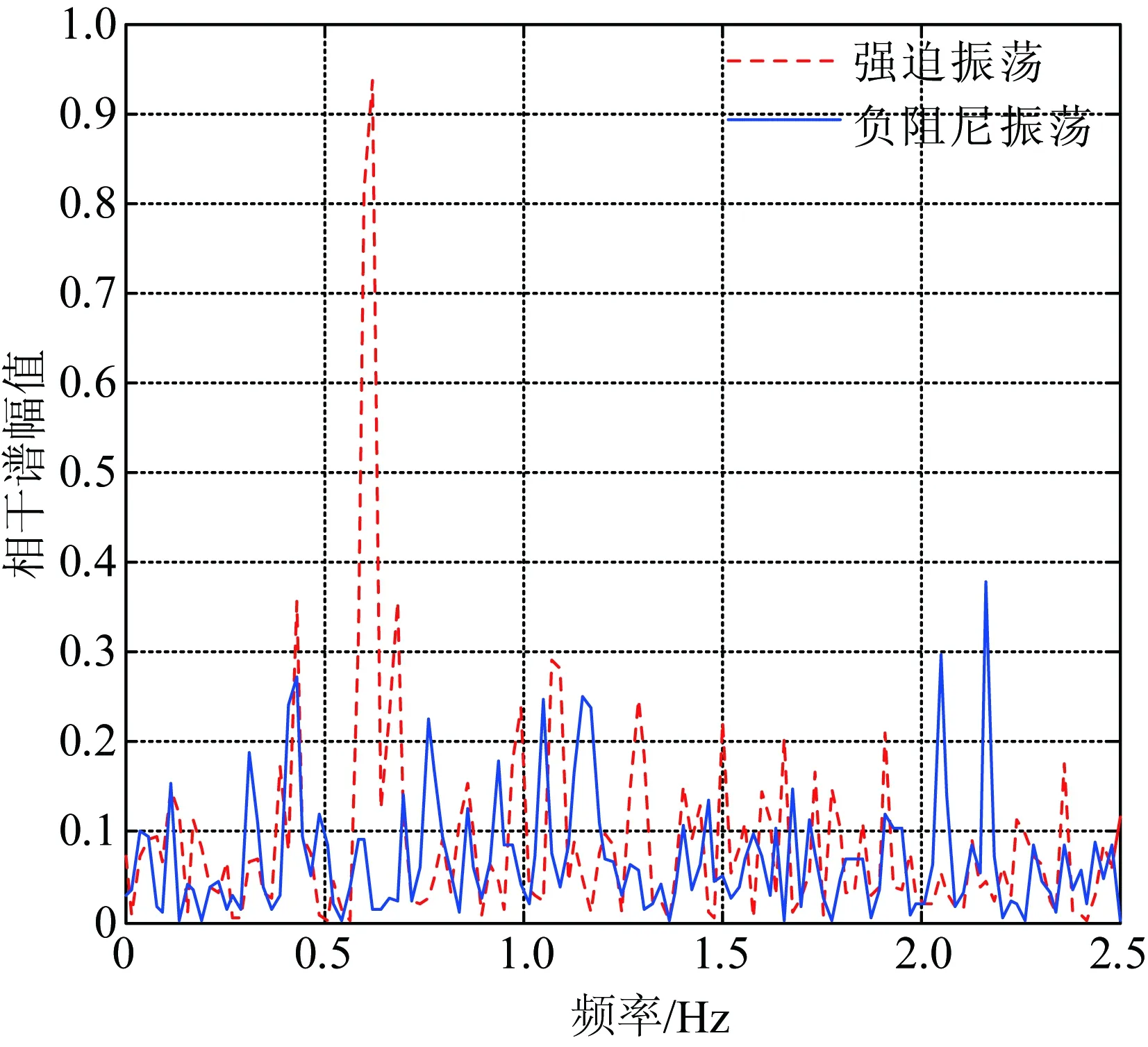
图6 基于发电机1和3有功功率的相干谱分析图

系统受到持续周期性扰动，扰动频率与系统固有振荡频率接近，引发系统发生强迫振荡。强迫振荡为同一个扰动源激励引发的系统振荡，各响应之间具有相同的振荡形式，频域响应信号之间可以近似线性表示。而对于负阻尼振荡，振荡初期，为多个振荡模式并存的，负阻尼作为主导振荡模式并不凸显，频域响应信号之间不能线性表示。从图5和图6相干谱图中分析可知，相干性分析的输入信号无论是选择电气距离较近的同一区间2台发电机组的有功功率还是距离较远的不同区间发电机组的有功功率，强迫功率振荡在相干谱分析图中0.625 Hz附近均出现尖峰，与外施扰动源扰动频率0.62 Hz差距较小，且相干谱峰值均大于设定阈值0.7；负阻尼振荡峰值远小于阈值0.7，与第2节的理论分析得到了一致结论。因此，通过对相干谱峰值的分析比较，有效识别出系统的振荡类型。

4.2 系统噪声强度对振荡类型识别的影响

在实际系统中，运行人员的操作方式和系统的电压等级大小均会影响系统的噪声分贝大小，使系统呈现不同的信噪比。本文中，信噪比分别取10，15，20 dB，计算不同信噪比下强迫振荡的幅值平方相干函数。相干谱对比分析如图7所示。

图7 3种信噪比下强迫振荡相干谱对比分析

系统发生强迫振荡时，系统响应中含有强迫振荡和噪声2部分，因此，相干谱图中峰值不会达到1。由图7可以看出，随着系统信噪比降低，即随着系统噪声强度的增加，相干谱峰值逐渐减小，但仍大于给定阈值。说明本文提出的振荡识别方法具有一定的抗噪性。但如果系统噪声强度过大，则可能导致本文振荡类型识别方法失误。通过大量反复试验仿真，在信噪比低于-10 dB的情况下，本文判别方法将失效。

5 结 论

(1)相比于采用稳态数据的传统分析方法，本文利用振荡初期数据，在振荡发生后很短的时间内快速识别振荡类型，为调度员采取紧急控制措施提供依据，具有良好的实时性；

(2)本文提出的振荡类型识别方法是对现有识别方法的一个补充，即在强噪声环境下准确识别2种振荡类型，具有一定的抗噪性；

(3)电力系统是一个典型的非线性系统，低频振荡中仍存在一些用负阻尼机理和强迫振荡机理无法解释的问题，如何优化判据，使之更加精确地识别出低频振荡类型是需要进一步改进的地方。

[1]DEMELLO F.Concepts of synchronous machine stability as affected by excitation control[J].IEEE Transactions on Power Apparatus and Systems，1969，88(4)：316-329.

[2]王慧铮，王铁强，许勇，等.基于WAMS与PSD的电力系统低频振荡起振原因分析[J].电力建设，2010，31(10)：1-5. WANG Huizheng, WANG Tieqiang, XU Yong, et al. Analysis of low frequency oscillation of the WAMS and PSD-based power system[J].Electric Power Construction,2010,31(10):1-5.

[3]郑伟，周喜超，杨俊.甘肃嘉酒电网低频振荡分析与治理[J].电力建设，2010，31(10)：53-55. ZHENG Wei, ZHOU Xichao, YANG Jun, et al. Analysis and harnessing of low frequency oscillation in Gansu Jiajiu power grid[J].Electric Power Construction,2010,31(10):53-55.

[4]KUNDER P.Power system stability and control[M].New York，NY，USA：McGraw-Hill，1944.

[5]汤涌.电力系统强迫功率振荡的基础理论[J].电网技术，2006，30(10)：29-33. TANG Yong.Fundamental theory of forced power oscillation in power system[J].Power System Technology，2006，30(10)：29-33.

[6]王铁强，贺仁睦，王卫国，等.电力系统低频振荡机理的研究[J].中国电机工程学报，2002，22(2)：21-25. WANG Tieqiang，HE Renmu，WANG Weiguo，et al.The mechanism study of low frequency oscillation in power system[J].Proceedings of the CSEE，2002，22(2)：21-25.

[7]竺炜，周有庆，谭喜意，等.电网侧扰动引起共振型低频振荡的机制分析[J].中国电机工程学报，2009，29(25)：37-42. ZHU Wei，ZHOU Youqing，TAN Xiyi，et al.Mechanism analysis of resonance-type low-frequency oscillation caused by networks side disturbance[J].Proceedings of the CSEE，2009，29(25)：37-42.

[8]顾丽鸿，周孝信，陶洪铸，等.局部弱联诱发互联电网强迫振荡机制分析[J].电网技术，2010，34(12)：36-43. GU Lihong，ZHOU Xiaoxin，TAO Hongzhu，et al.Analysis on mechanism of inter-area forced oscillation caused by local weak interconnection in interconnected power grid[J].Power System Technology，2010，34(12)：36-43.

[9]杨毅强，刘天琪，李兴源，等.电力系统强迫功率振荡的等效电路定位分析法[J].电网技术，2012，36(11)：101-108. YANG Yiqiang，LIU Tianqi，LI Xingyuan，et al.An equivalent circuit approach to locate source of power system forced power oscillation[J].Power System Technology，2012，36(11)：101-108.

[10]杨东俊，丁坚勇，李继升，等.基于参数辨识的强迫功率振荡扰动源定位方法[J].电力系统自动化，2012，36(2)：26-30. YANG Dongjun，DING Jianyong，LI Jisheng，et al.A disturbance source location method for forced power oscillations based on parameter identification [J].Automation of Electric Power Systems，2012，36(2)：26-30.

[11]余一平，闵勇，陈磊，等.基于能量函数的强迫功率振荡扰动源定位[J].电力系统自动化，2010，34(5)：1-6. YU Yiping，MIN Yong，CHEN Lei，et al.Disturbance source location of forced power oscillation using energy functions[J].Automation of Electric Power Systems，2010，34(5)：1-6.

[12]李莹，贾文双，李文锋，等.基于起振段波形在线判别电力系统功率振荡性质[J].中国电机工程学报，2013，33(25)：54-60. LI Ying，JIA Wenshuang，LI Wenfeng，et al.Online identification of power oscillation properties based on the initial period of wave[J].Proceedings of the CSEE，2013，33(25)：54-60.

[13]代贤忠，沈沉.基于端口供给能量分解的电力系统振荡类型区分方法[J].电力系统自动化，2014，38(23)：40-45. DAI Xianzhong，SHEN Chen.A power system oscillation property identifying method based on decomposition of energy supply on port[J].Automation of Electric Power Systems，2014，38(23)：40-45.

[14]马燕峰，刘伟东，赵书强.基于包络线拟合的低频振荡性质在线判别[J].电力系统自动化，2014，38(23)：46-54. MA Yanfeng，LIU Weidong，ZHAO Shuqiang.On-line identification of low-frequency oscillation properties based on envelope fitting[J].Automation of Electric Power Systems，2014，38(23)：46-54.

[15]吕雯雯.基于信号相干统计理论的周期性信号检测[D].长春：吉林大学，2009. LYU Wenwen.Detecting periodic signals based on a statistical theory of signal coherence[D].Changchun：Jilin University，2009.

[16]NING Z.Initial results in using a self-coherence method for detecting sustained oscillations[J].IEEE Transactions on Power Systems，2015，30(1)：522-530.

(编辑 张媛媛)

Low Frequency Oscillation Type Discrimination Based on Initial Oscillation Waveform Data and Coherence Method

WANG Lixin, CAI Guowei, YANG Deyou, SUN Zhenglong

(School of Electrical Engineering, Northeast Dianli University, Jilin 132012, Jilin Province, China)

According to the different excitations, the main low frequency oscillation of power system is forced oscillation and negative damping oscillation. The two kinds of oscillations are similar in form, but the control methods are quite different. We summarize the external characteristic and distinction of the two kinds of oscillations based on the deep analysis on the analytical expression of active power oscillation of power system, then put forward a oscillation type identification method on the basis of coherence method. Firstly, this method obtains two sets of initial data of oscillation which contains the noise through the wide area measurement system (WAMS) installed on the different generators, then calculates the magnitude squared coherence of the two sets of data based on coherence method. So we can identify the oscillation type by the comparison of the magnitude squared coherence. The simulation calculation and analysis of four-machine, two-area system verify the feasibility and effectiveness of the proposed identification methods.

power system; low frequency oscillation; forced power oscillation; negative damping oscillation; coherence method

国家自然科学基金项目(51507028)

TM 712

A

1000-7229(2016)10-0108-06

10.3969/j.issn.1000-7229.2016.10.015

2016-03-15

王丽馨(1991)，女，硕士研究生，主要研究方向为电力系统稳定分析与控制；

蔡国伟(1968)，男，教授，主要从事电力系统运行分析方面的教学与科研工作；

杨德友(1983)，男，副教授，研究方向为电力系统稳定性分析及大规模可再生能源并网；

孙正龙(1988)，男，博士研究生，主要从事电力系统频率稳定方面的研究工作。

Project supported by National Natural Science Foundation of China(51507028)