计及谐波相序特性的配电网谐波潮流改进算法

宋梦琪，陶顺

(新能源电力系统国家重点实验室(华北电力大学)，北京市 102206)

计及谐波相序特性的配电网谐波潮流改进算法

宋梦琪，陶顺

(新能源电力系统国家重点实验室(华北电力大学)，北京市 102206)

由于不同频次的谐波具有不同的相序特性，提出计及谐波相序特性的配电网谐波潮流改进算法。首先分析各频次谐波的相序特性，然后推导变压器的谐波相序模型，综合考虑变压器联结方式、联结组别和中性点接地阻抗等对谐波潮流分析的影响；并讨论其他元件的谐波相序模型。在此基础上，实现MATLAB程序化的分相序谐波潮流分析。最后，以IEEE33节点系统和某个含光伏电站的实际配电网系统为例，通过计算并与不计及相序特性的潮流计算结果及PSCAD的仿真结果进行对比，证明了所提方法的有效性和准确性。

谐波潮流；相序特性；变压器；配电网

0 引 言

基于电力电子接口的新能源与新型非线性负荷的接入，使得配电网的谐波源种类和数量都大量增加，谐波问题变得更加严重。谐波会对电力系统和用户造成一系列危害，如增加附加发热和损耗，造成设备故障[1]，影响电能计量等。开展谐波潮流分析，了解谐波在配电网中的分布是谐波评估和治理的基础。

已有诸多文献对谐波潮流的计算方法进行了研究，谐波潮流计算在数学上可归结为对谐波网络方程和谐波源特性方程的求解[2]，可分为统一谐波潮流法、迭代谐波分析法和基于恒流源模型的方法等[3-8]，其中应用最为广泛的是基于谐波源恒流源模型的方法[7-11]，其能实现基波潮流与谐波潮流的解耦计算，求解快速。但在现有的谐波潮流计算研究中，绝大多数文献[4-6,12-13]对各频次谐波的相序特性不作区分，不考虑由此带来的元件模型及参数和网络拓扑的变化对谐波潮流的影响。

文献[14]在计算发电机谐波等值阻抗时计及了不同频次谐波的相序对其参数大小的影响，但未建立线路和变压器的谐波相序模型。对于变压器模型，现有的谐波潮流算法广泛采用理想变压器串联阻抗的形式[6,12-15]，并不考虑谐波相序特性的影响。文献[16]虽然考虑了谐波相序对变压器零序等值电路的影响，将除了YNyn联结以外的其他类型变压器的零序阻抗都等效为无穷大，但明显不适用于YNd联结形式。文献[1]在用对称分量法分析三相不对称谐波潮流时，仅对几种联结组别的变压器在正、负序等值电路中的移相角度进行了说明，且未讨论零序模型。另外，上述文献均没有考虑中性点接地阻抗对零序通路的影响，以及变压器的联结组别对零序下电压或电流方向的影响。

计及各频次谐波的相序特性，本文提出一种分相序计算的改进谐波潮流计算方法，其中，应用变压器的原副边电压、电流关系，考虑不同联结方式、联结组别和中性点接地方式的变压器在各相序下的特点，系统推导适用于谐波潮流分相序计算的变压器模型。最后以IEEE33节点系统和某个含光伏电站的实际配网为例，验证该方法和变压器模型的合理性和有效性。

1 各次谐波的相序特性

谐波相序与谐波频次有关，不同频次谐波下的三相分属不同的序分量系列，分析如下文。

对称的三相非正弦周期性相电压/电流在时间上依次滞后1/3个周期(正序)[17]，有：

fA=f(t)

(1)

(2)

(3)

式中：fA，fB，fC分别表示A、B、C三相的相电压/电流；t为时间变量；T为周期。

将fA、fB、fC进行傅里叶分解，有：

fA=∑F(h)cos(hw1t+φh)

(4)

(5)

(6)

式中：h为谐波次数；F(h)为h次谐波电压/电流的幅值；w1=2π/T为基波角频率；φh为第h次谐波的初相角。

比较各次谐波电压/电流的相位差，可得到结论如下。

(1)当h=3n+1，n=0，1，2……(自然数)，即h=1，4，7……时，各相中该系列谐波的电气量的初相位分别为

可见，这些频次下的谐波都是正序性的。

(2)当h=3n+2，n=0，1，2……(自然数)，即h=2，5，8……时，各相中该系列谐波的电气量的初相分别为

可见，这些频次下的谐波都是负序性的。

(3)当h=3n，n=0，1，2……(自然数)，即h=3，6，9……时，各相中该系列谐波的电气量的初相分别为

A相：φh；B相：φh-2nπ；C相：φh+2nπ

可见，这些频次下的谐波都是零序性的。

由以上分析可知，三相对称的非正弦周期量的级数展开式中的谐波组合为3类对称组，即正序对称组、负序对称组和零序对称组。

对于不同的序分量系列，电力元件的参数和模型不同，且电流通路不同，不区分不同频次谐波的相序特性显然是不准确的。谐波潮流需要建立能够体现不同频次谐波相序特性的元件模型分相序计算。

2 变压器谐波相序模型

准确的变压器模型要满足基尔霍夫电流定律和基尔霍夫电压定律，还要考虑变压器的变比、联结方式、联结组别，当变压器经接地阻抗接地时，还应计及接地阻抗对谐波潮流的影响。

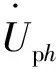
下面就各频次谐波的相序特性推导基于节点电压矩阵的变压器谐波潮流计算模型。

2.1 正序性谐波下

正序性的三相电压/电流对称且相位互差120°，当存在接地阻抗时流经接地阻抗的电流为0，因此在正序情况下分析原副边电路关系时不考虑接地阻抗。设正序下原边电压相对副边电压的相位偏移为θ，令n=nT∠θ，则n*=nT∠-θ。则存在：

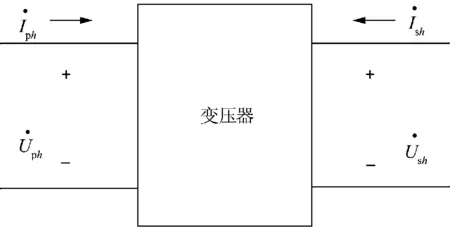
图1 变压器等效模型

(7)

(8)

即有

(9)

式中h=4，7，10……,θ与变压器的联结组别有关，由文献[18]的分析可知，当变压器为YNd11联结时，θ=30°。应用文献[18]中的推导方法对各联结组别下的变压器进行分析，设变压器联结组的时钟序数为x，则θ=30x。

2.2 负序性谐波下

负序与正序类似，不必考虑接地阻抗，但负序下的原副边相位偏移为正序的相反数。则：

(10)

(11)

可得：

(12)

式中h=2，5，8……。

2.3 零序性谐波下

在零序情况下(谐波频次h取值为3，6，9……)，变压器的不同联结方式会影响零序通路的结构，并且由于三相电流相等，接地支路有电流流过，不能忽略接地阻抗的影响。假设原边的接地电阻和电抗分别为Rgp和Xgp，副边的接地电阻和电抗分别为Rgs和Xgs，则在h次谐波下，原边的接地谐波阻抗为Zgph=Rgp+jhXgp，副边为Zgsh=Rgs+jhXgs。若绕组为直接接地，则相应侧的接地谐波阻抗取0。

下面就变压器的不同连接方式分为4种情形对变压器的零序模型进行讨论。

(1)原、副边均有零序通路(YNyn)，绕组示意图如图2所示。

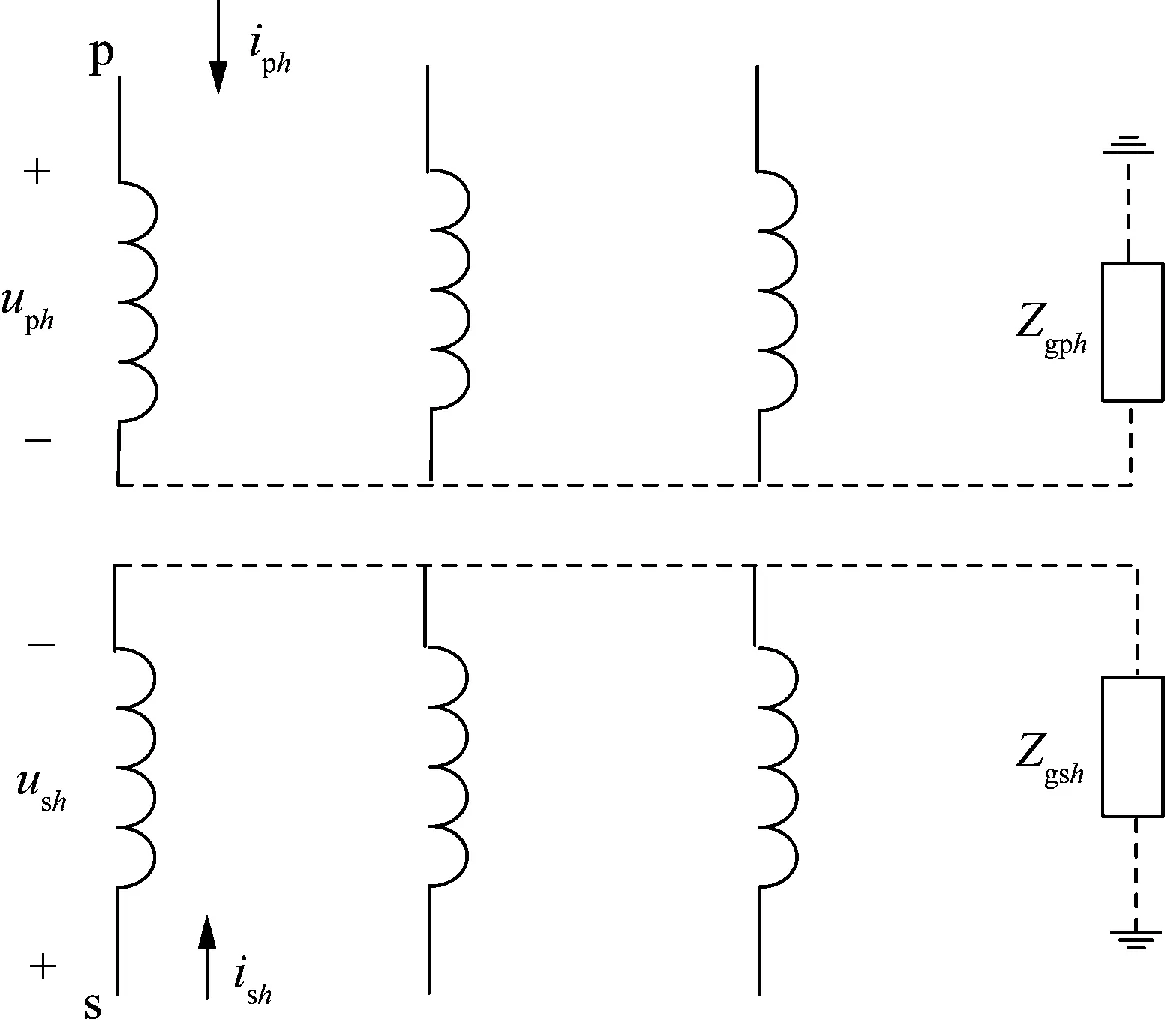
图2 三相变压器的绕组示意图

由图2分析可知，当三相变压器通入三相零序电流且原边/副边绕组接地时，可等效为原边/副边绕组串联3Zgph/3Zgsh的阻抗。将原边阻抗(包括接地阻抗)折合到低压侧，存在以下关系

(13)

电流之间有

(14)

式中n0为nT的修正值，用以反映变压器联结组别对原副边零序电路关系的影响。以电流关系分析为例，由于原副边均为Y联结且中性点接地，因此原副边零序电流同相或反相，当联结组标号的时钟序数为0、4、8时，在图1规定的电流参考方向下，原/副边零序电流从绕组同名端流入，此时n0=nT；而当时钟序数为2、6、10时，原/副边零序电流从绕组异名端流入，则n0=nT。

故有

(15)

(2)原边没有零序通路(Y或者D)，副边有零序通路(yn)。

则原边零序电流为

(16)

副边的电流电压关系类似于情形(1)，原边没有接地阻抗，则存在

(17)

所以有

(18)

(3)原边有零序通路(YN)，副边没有零序通路(y或者d)。

则副边电流有

(19)

由于副边没有通路，将ZT折合到原边，电压电流有如下关系

(20)

可得

(21)

(4)原副边都没有零序通路。

这种情况下原副边均不含零序电流，则有

(22)

由推导的变压器模型可知，如果忽略谐波的相序特性，对各次谐波采用相同的变压器模型进行谐波潮流分析是不合适的。

3 其他元件谐波相序模型

3.1 发电机模型

理想发电机电动势可以认为是纯正弦的，不含有谐波分量，因而发电机电动势只存在于基波网络。在谐波网络里，发电机电动势为0[15]。在正/负序性谐波作用下，其在h次谐波下的等值电路为由发电机端点经谐波阻抗ZGh直接与中性点相连，零序性谐波下，连接方式视发电机接地的情况而有所差异。发电机谐波相序模型如图3所示。

图3中，Zgh为h次谐波下的接地阻抗值，ZGh为发电机h次谐波下的阻抗值，有[19]。

(23)

式中：RG和XG分别为发电机的基波电阻和基波电抗，考虑谐波相序特性，则应视谐波频次取其相应相序的值。

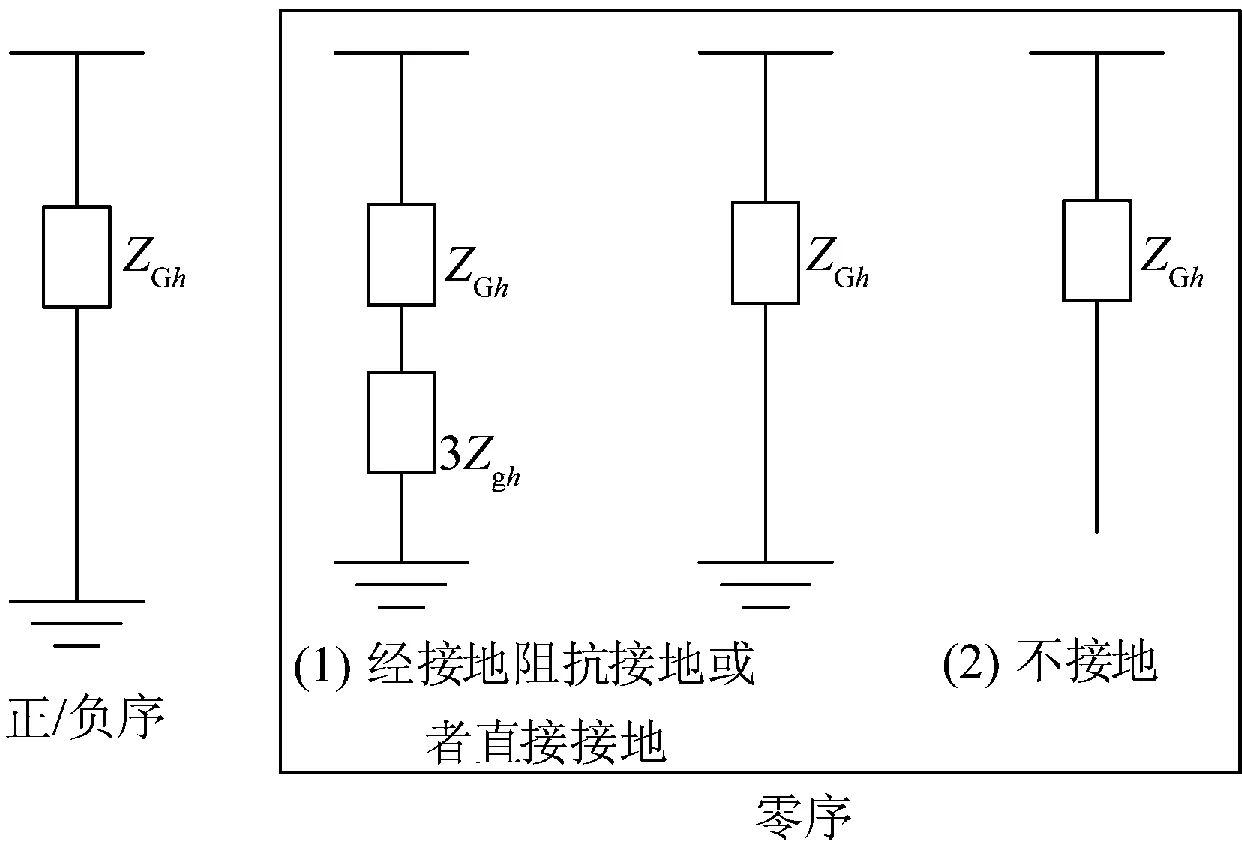
图3 发电机谐波相序模型

3.2 线路模型

由于配电网线路较短，其谐波模型可采用Π形等值电路，如式(24)和式(25)所示：

ZLh=RL+jhXL

(24)

YLh/2=jhBL/2

(25)

式中：ZLh为线路在h次谐波下的阻抗值；YLh为线路在h次谐波下的导纳值；RL、XL、BL分别为线路在基波情况下的参数值，视谐波频次取相应相序的值。

3.3 负荷模型

在谐波潮流中一般以等效恒定阻抗Zsh表示负荷[13]。假设节点有功负荷为P，无功负荷为Q，负荷等效谐波阻抗Zsh计算如下所示：

(26)

RS=U2P/S2

(27)

XS=U2Q/S2

(28)

式中：RS、XS分别为基波时的等值电阻和等值电抗；U为节点电压；S为节点视在功率。

4 谐波潮流计算方法和流程

谐波潮流计算是研究谐波特性和分析电能质量的重要手段。目前，在工程计算中多采用恒流源模型对谐波源进行建模，应用式(29)所示的谐波网络方程进行各次谐波潮流计算。由该公式可知，配电网在各频次谐波下的模型和计算是独立的。

Ih=YhUh

(29)

式中：Uh、Ih分别为h次谐波电压、电流矩阵；Yh为系统h次谐波导纳矩阵。

在谐波潮流分相序计算中，第h次谐波潮流计算过程的程序框图如图4所示。

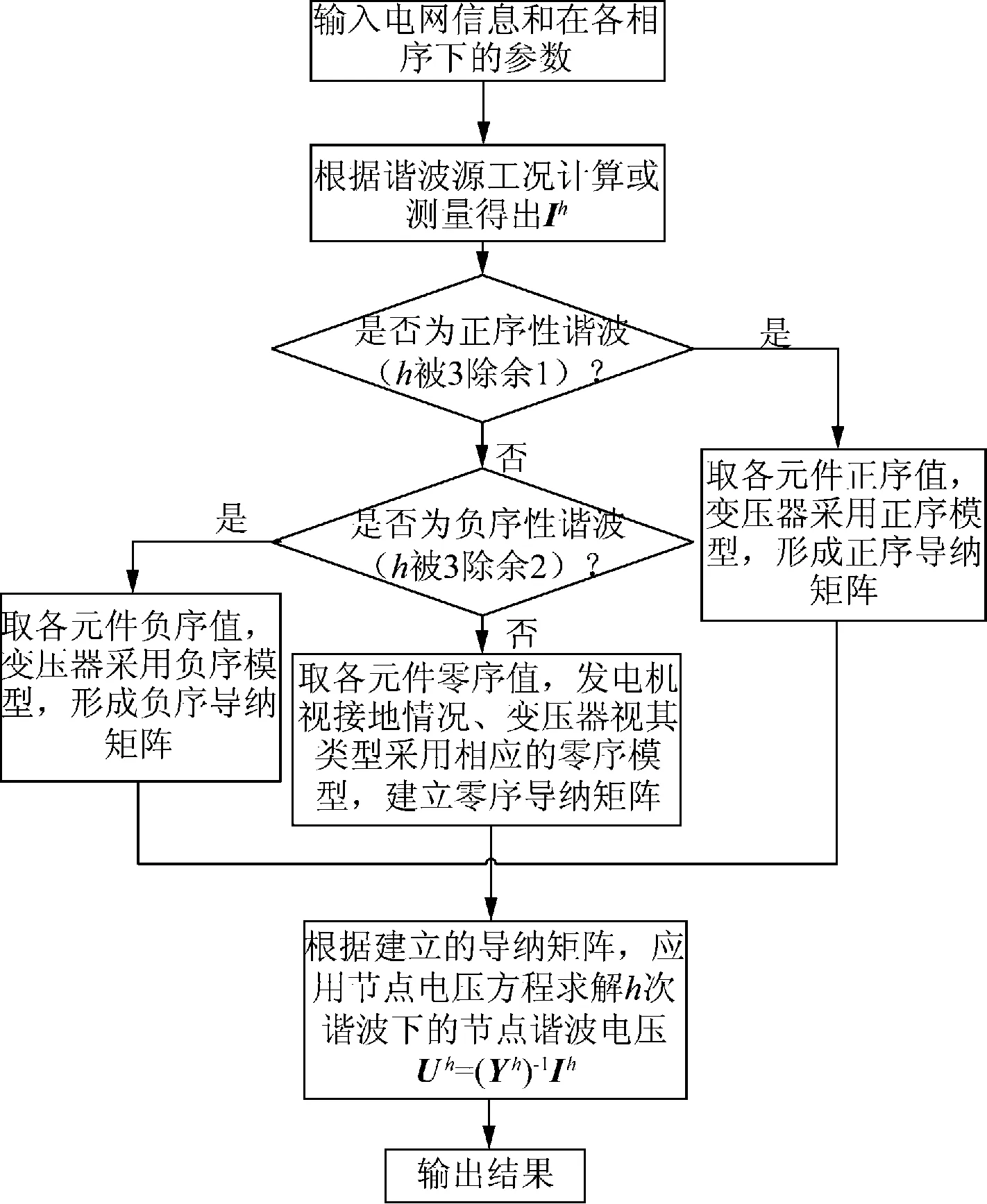
图4 第h次谐波的分相序谐波潮流计算的程序框图

由图4可见，该算法通过判断谐波的不同相序特性，在不同相序下的谐波潮流计算中，采用元件的不同相序参数，尤其是对不同相序采用相应的变压器模型，来反映各元件对各序潮流的影响。

5 算例分析

根据该算法编制的MATLAB程序对2个配电网系统进行谐波潮流计算，并与PSCAD的仿真结果进行了对比。

5.1 含变压器的某光伏电站配电网系统

前文推导了变压器谐波相序模型，考虑了变压器联结方式、联结组别和中性点接地阻抗等问题，本算例以Yd11变压器为例，对推导的变压器谐波相序模型在谐波潮流计算中应用的正确性进行验证。根据该算法编制的程序对接入光伏电站的某实际110 kV配电网的系统模型进行谐波潮流计算，该光伏电站算例结构如图5所示，5个光伏电站分别通过5个相同型号的配电变压器接入配电网，变压器为Yd11联结，变比为110 kV/0.29 kV。将主网等效成为一个发电机模型，三相基准功率为100 MV·A，线电压基准值为110 kV。其中节点0为并网节点，节点2—6均为光伏接入节点，5个光伏逆变器型号相同，单台逆变器注入谐波电流的数据如表1所示。

图5 含光伏电站配网系统

由于发电机的负序电抗一般为正序的0.134～0.350倍，零序电抗一般为正序的0.036～0.125倍[20]，本文中的算例分别取值为0.134和0.036。

采用本文所提计算方法对该网络进行谐波潮流计算，并将得到的节点谐波电压和线路(节点0～1)的谐波电流与不计及相序方法的计算结果及PSCAD的仿真结果进行对比。其中，3—5次谐波的对比结果如表2和表3所示。

表2 谐波电压的部分对比结果

Table 2 Partial comparison results of harmonic voltage

表3 线路谐波电流的部分对比结果

由表2可知，与不计及谐波相序的计算方法相比，零序和负序性谐波电压的结果差异明显。对于3次谐波，由于Yd联结的变压器不能提供零序通路，谐波不能通过变压器，节点0、1的谐波电压均为0，而不计及相序的计算则不能体现这一点；而对于5次谐波来说，由于正负序下变压器的相位偏移以及发电机的参数不同，因此是否计及相序特性对计算结果带来较大影响。表3中，对于谐波电流来说，谐波源电流通过变压器在正负序下的差异主要在于相位偏移，因此2种方法得到的谐波电流幅值相同，而零序性谐波的计算结果由于计及相序没有零序通路而呈现较大差别。

综合上述分析可知，以PSCAD仿真结果为参考，采用本文计算方法的程序计算结果的误差均在合理范围内。该案例含变压器模型，显然本文的变压器模型在计及谐波相序的谐波潮流计算中是正确的，具有工程应用价值。

5.2 IEEE33节点系统

对IEEE33节点系统进行谐波潮流计算。测试系统的模型结构如图6所示：将主网等效成为一个发电机模型，三相基准功率为100 MV·A，线电压基准值为12.66 kV。其中节点0为并网节点，其他节点均为负荷节点。谐波源注入数据如表4和表5所示。

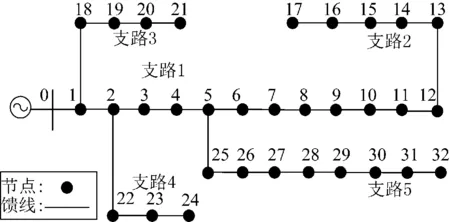
图6 IEEE33节点试验系统

表5 5和7次谐波源参数

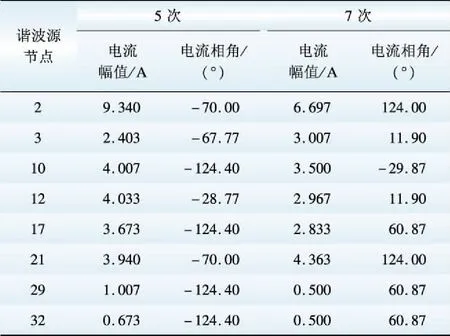
采用前述元件谐波相序模型和谐波潮流算法实现了分相序谐波潮流分析，并与传统的不计及谐波相序特性的谐波潮流分析结果进行了对比。其中，3次(零序性)和5次(负序性)谐波电压的分析结果对比分别如图7和图8所示。

图7 3次谐波潮流分析结果对比

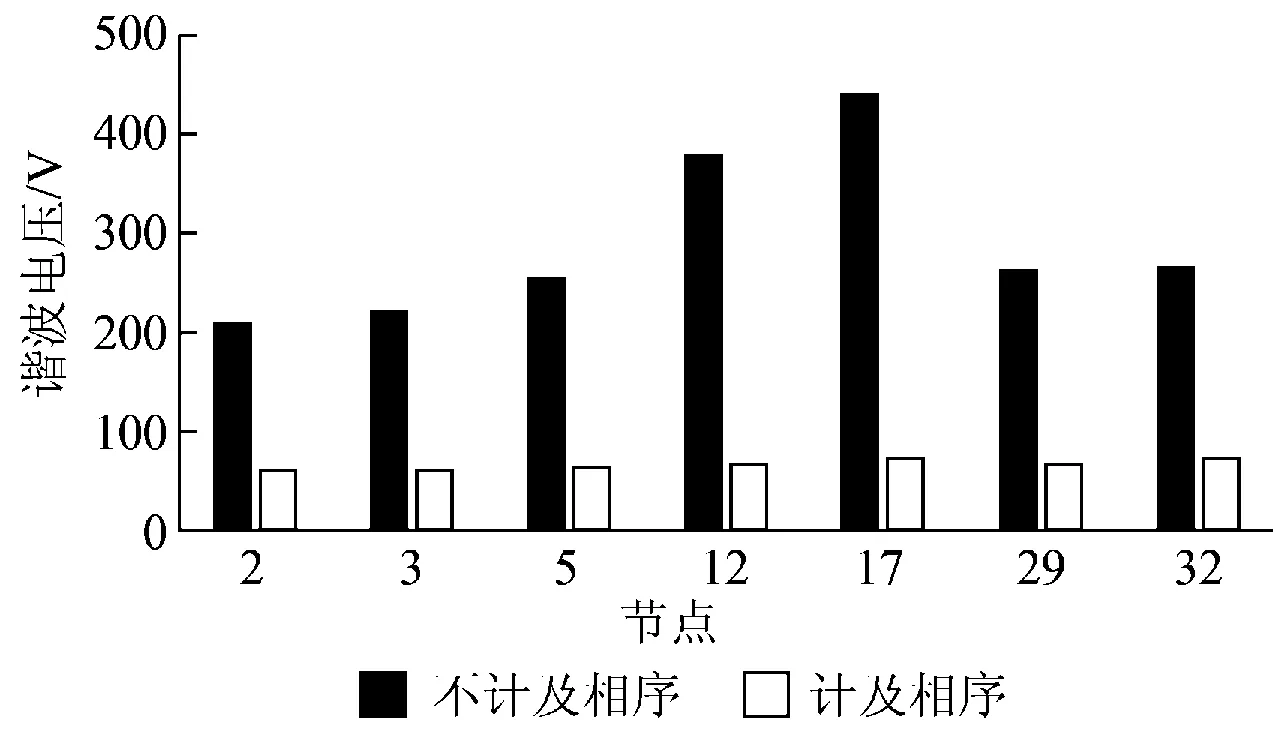
图8 5次谐波潮流分析结果对比

由图7、8可见，是否计及谐波的相序特性对谐波潮流分析结果的影响非常大。

分相序谐波潮流计算结果与PSCAD仿真结果对比如表6所示。

表6 分相序谐波潮流分析与PSCAD仿真对比结果

Table 6 Comparison between harmonic power flow computation and simulation results in PSCAD with considering sequence characteristics V

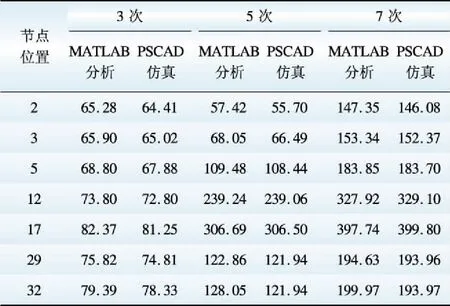
由表6可知，计及谐波频次相序特性的谐波潮流分析结果与PSCAD仿真结果相比，误差较小，结合图7、8的对比证明了本文所提计算方法的正确性。

6 结 论

本文提出了一种考虑不同谐波相序特性的改进谐波潮流计算方法，讨论了各相序下的电网元件谐波模型与参数。其中，对各相序的变压器模型进行了推导，将变压器的不同联结方式、联结组别、中性点接地阻抗等带来的影响计及在内，并基于所提模型和方法实现了谐波分相序潮流计算，可用于配电网的三相对称谐波潮流分析。与其他谐波分析程序相比，本文所采用的方法计及了谐波的相序特性，系统地建立了各类型变压器的相序模型，更加准确。最后以含有变压器的某实际110 kV配网与不含变压器的IEEE33节点系统为例，验证了变压器模型和该计算方法的合理性和工程实用价值。

在实际工程中，配电网的谐波源并不总是对称的，往往要用到对称分量法来计算。本文的变压器及其他元件的模型和计算方法考虑了相序特性，适用于对称分量法的各相序计算，因此同样适用于三相不对称谐波源情况下的谐波潮流计算，具有广泛的实际应用价值。

[1]顾伟,陈谦,蒋平. 基于对称分量坐标的配电网谐波潮流计算模型[J]. 电力系统及其自动化学报,2004,16(1):1-5,73. GU Wei, CHEN Qian, JIANG Ping. Distribution harmonic power flow models based on symmetrical component coordinate system[J]. Proceedings of the EPSA,2004,16(1):1-5,73.

[2]王守相,张颖,韩亮. 配电系统三相不确定谐波潮流的复仿射计算方法[J]. 电力系统自动化,2015,39(7):41-46，110. WANG Shouxiang, ZHANG Ying, HAN Liang. A complex affine calculating method for three-phase uncertain harmonic power flow in distribution system[J]. Automation of Electric Power Systems,2015,39(7):41-46,110.

[3]孙媛媛,王小宇,尹志明. 多谐波源系统的非迭代式谐波潮流分析[J]. 中国电机工程学报,2012,32(7):83-90,195. SUN Yuanyuan, WANG Xiaoyu, YIN Zhiming. Non-iterative harmonic power flow analysis for power systems with multiple harmonic sources[J]. Proceedings of the CSEE,2012,32(7):83-90,195.

[4]潘云江,赵书强,陈斌发,等. 电力系统不对称谐波潮流的一种实用计算方法[J]. 电力系统自动化,2000,24(9):60-62. PAN Yunjiang, ZHAO Shuqiang, CHEN Binfa, et al. A practical computation method for unsymmetrical harmonic power flow[J]. Automation of Electric Power Systems,2000,24(9):60-62.

[5]卢恩,张步涵,龚世缨. 电力系统谐波潮流的一种解耦算法[J]. 电网技术,2003,27(2):34-36,71. LU En, ZHANG Buhan, GONG Shiying. A decoupled algorithm for power system harmonic flows[J].Power System Technology,2003,27(2):34-36,71.

[6]崔威,李建华,赵娟. 供电网络谐波潮流计算[J]. 电力自动化设备,2003,23(2):11-14. CUI Wei, LI Jianhua, ZHAO Juan. Harmonic flow calculation in power supply system[J]. Electric Power Automation Equipment,2003,23(2):11-14.

[7]BONNER A, GREBET, GUNTHER E, et al．The modeling a-nd simulation of the propagation of harmonics in electric power networks, part I: concepts, models and simulation techniques[J]．IEEE Transactions on Power Delivery, 1996,11(1):452-465.

[8]CHANG G, HATZIADONIUC, XU W, et al. Modeling devices with nonlinear voltage-current characteristics for harmonic studies[J]. IEEE Transactions on Power Delivery,2004, 19(4):1802-1811.

[9]Teng J H, Chang C Y. Backward/forward sweep-based harmonic analysis method for distribution systems[J]. IEEE Transactions on Power Delivery, 2007, 22(3): 1665-1672.

[10]余光正,林涛,徐遐龄,等. 基于2m+1点估计法的考虑风力发电接入时电力系统谐波概率潮流算法[J]. 电网技术,2015,39(11):3260-3265. YU Guangzheng, LIN Tao, XU Xialing, et al. An algorithm based on 2m+1 point estimate method for harmonic probabilistic load flow calculation of power systems incorporating wind power[J]. Power System Technology,2015,39(11):3260-3265.

[11]王斌,姜晓锋,黄文,等. 高速铁路车网耦合下的谐波潮流计算方法研究[J]. 电力系统保护与控制,2014,42(17):15-23. WANG Bin, JIANG Xiaofeng, HUANG Wen, et al. Harmonic load-flow approach based on train-catenary coupling system of high-speed railway[J]. Power System Protection and Control,2014,42(17):15-23.

[12]盛美卫. 考虑分布式电源谐波随机性的随机谐波潮流计算[D].武汉：华中科技大学,2013. SHENG Meiwei. Research on stochastic harmonics power flow with considering the randomness of harmonics generated by distributed generators[D]. Wuhan: Huazhong University of Science & Technology, 2013.

[13]许璐,袁越,王敏,等. 含电动汽车充电站的配电网谐波潮流计算[J]. 现代电力,2014,31(2):21-26. XU Lu, YUAN Yue, WANG Min, et al. Harmonic power flow calculation of distribution network with electric vehicle charge station[J].Modern Electric Power,2014,31(2):21-26.

[14]巩翔宇. 含分布式电源的配电网谐波潮流计算分析[D].郑州：郑州大学,2015. GONG Xiangyu. Analysis of distributed power distribution network harmonic power flow calculation[D]. Zhengzhou: Zhengzhou University, 2015.

[15]顾伟,陈谦,蒋平. 采用对称分量坐标的谐波潮流部分解耦算法[J]. 电力自动化设备,2004,24(2):9-13. GU Wei, CHEN Qian, JIANG Ping. Partly decoupled harmonic flow in symmetrical component coordinate system[J]. Electric Power Automation Equipment, 2004, 24(2): 9-13.

[16]周星伯. 含分布式电源的配电网谐波概率潮流[D].北京：华北电力大学,2014. ZHOU Xingbo. Harmonic probabilistic power flow of distribution network with distributed generation[D]. Beijing: North China Electric Power University,2014

[17]邱关源,罗先觉.电路[M].北京：高等教育出版社, 2006.

[18]张伯明,陈寿孙,严正.高等电力网络分析[M].北京：清华大学出版社, 2007

[19]ARRILLAGA J, WATSON N R, CHEN S. Power system quality assessment[M]. Chichester, England; New York: John Wiley & Sons, 2000.

[20]韩祯祥.电力系统分析[M].杭州：浙江大学出版社, 2005.

(编辑 刘文莹)

An Improved Calculation Method of Distribution Network Harmonic Power Flow Considering Phase Sequence Characteristics of Harmonics

SONG Mengqi, TAO Shun

(State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China)

As different order harmonics have different phase sequence characteristics, this paper proposes an improved calculation method of harmonic power flow for distribution network. Firstly, we analyze the phase sequence characteristics of harmonics. Next, we deduce the transformer models under different harmonic phase sequence with taking the impacts of transformer’s winding connection modes, connection set and neutral point grounding impedance on harmonic power flow into account; and discuss the calculation model of other electrical elements of distribution system with considering phase sequence. On this basis, the harmonic power flow with different phase sequences in MATLAB we analyzed. Finally, taking the IEEE 33-bus system and a practical distribution network including photovoltaic power station as examples, the power flow with or without considering phase sequence characteristics was calculated and the results were compared with the simulation results in PSCAD, which verify the feasibility and correctness of the proposed method.

harmonic power flow; phase sequence characteristics; transformer; distribution network

国家自然科学基金项目(51207051)

TM 72

A

1000-7229(2016)10-0100-08

10.3969/j.issn.1000-7229.2016.10.014

2016-05-18

宋梦琪(1992)，女，硕士研究生，主要研究方向为电能质量；

陶顺(1972)，女，副教授，博士，主要研究方向为智能配电网和电能质量等。

Project supported by the National Natural Science Foundation of China (51207051)