基于等效开环过程的VSC-HVDC阻尼控制器协调控制鲁棒稳定性研究

李志晗，张英敏，李兴源，邓旗

(四川大学电气信息学院，成都市 610065)

基于等效开环过程的VSC-HVDC阻尼控制器协调控制鲁棒稳定性研究

李志晗，张英敏，李兴源，邓旗

(四川大学电气信息学院，成都市 610065)

针对包含柔性直流(voltage source converter-high voltage direct current, VSC-HVDC)的交直流互联系统区间低频振荡现象，通过多变量系统等效开环过程(effective open-loop process，EOP)理论，将多变量系统回路方程转换为单变量系统回路方程，建立起各回路独立的数学模型。由于包含VSC-HVDC 的系统是多输入多输出复杂非线性系统，其中各回路阻尼控制器之间可能存在不协调的问题，基于小增益定理，在实现系统等效开环过程控制的基础上，提出判断各附加阻尼控制器间协调控制鲁棒稳定性指标；设计能抑制低频振荡且能协作运行的发电机电力系统稳定器(power system stabilizer, PSS)附加阻尼控制器和VSC-HVDC附加阻尼控制器。最后在PSCAD/EMTDC中搭建包含VSC-HVDC的交直流四机两区域系统，仿真验证所提指标的有效性和所设计控制器的实用性。

柔性直流；等效开环过程；小增益定理；附加阻尼控制器；低频振荡

0 引 言

柔性直流(voltage source converter-high voltage direct current, VSC-HVDC)输电相对于传统高压直流输电具有诸多优势：能够独立控制与交流系统交换的有功和无功功率[1]，能够向无源网络输电，不存在换相失败等问题[2]。这些明显优于传统HVDC的功能使得VSC-HVDC具有广阔的应用前景，尤其是在大容量、远距离输电以及区域电力系统互联等方面均获得了广泛应用[3]。

近年来，已有不少学者进行利用 VSC-HVDC 的快速功率控制特性设计附加阻尼控制器来提高系统阻尼方面的研究[4-5]。然而，目前还鲜有关于VSC-HVDC的附加阻尼控制器间协调控制方面的研究。文献[6]基于Bang-bang控制原理的混合功率调制方法来提高发电机阻尼，可以增强系统的阻尼并有效地抑制振荡。文献[7]基于整个系统的线性化方程，用线性最优控制理论设计了发电机励磁与VSC-HVDC之间协调优化方案。文献[8]针对交/直流并联系统中电力系统稳定器(power system stabilizer, PSS)与VSC-HVDC附加阻尼控制器之间的协调问题，提出基于参数约束线性优化方法的阻尼控制器参数优化算法。文献[9]基于同伦变换理论设计了有功、无功相协调的分散鲁棒控制器，能有效抑制低频振荡，在严重故障情况下能充分利用基于电压源换流器的直流输电的有功和无功调制能力。

上述文献均是依靠相关理论设计或优化了对应的协调控制器，但是VSC-HVDC是一个复杂的多输入多输出系统，设计控制器时常需考虑所设计控制器之间是否协调的问题。但在抑制VSC-HVDC系统中存在的低频振荡问题时，有可能在新增阻尼控制器时因控制器设计不当而导致当多个控制器一起投入时，其控制效果反而不如单个控制器投入。因此，本文提出针对包含柔性直流输电系统的交直流互联系统中发电机PSS附加阻尼控制器和VSC-HVDC附加阻尼控制器协调控制鲁棒稳定性指标，该指标表征多个附加控制器间相互作用的问题，包含了附加控制器设计不同而使其加入控制器后造成系统函数不同的问题。首先，在等效开环过程理论的基础上，针对多输入多输出系统，将多变量系统回路方程转变为单变量系统回路方程，不仅包含各回路之间的相互作用，而且使得控制回路形式更为简单；同时建立包含VSC-HVDC的交直流系统附加阻尼控制器间的等效开环过程，结合小增益定理，推导和提出判断系统附加阻尼控制器间协调控制鲁棒稳定性量化指标；在PSCAD/EMTDC中针对包含VSC-HVDC的交直流系统中发电机PSS附加阻尼控制和VSC-HVDC附加阻尼控制的协调问题进行了仿真验证。

1 等效开环过程

在一个如图1所示的多输入多输出系统中[10]，其中ri(i=1,2,…,n)为参考输入变量，ui(i=1,2,…,n)为控制变量，yi(i=1,2,…,n)是系统输出变量。

图1 多输入多输出系统

G(s)是控制变量和输出变量的传递函数矩阵，Gc(s)是控制函数矩阵，二者具有相同的阶数，形式如下：

(1)

(2)

对于控制变量uj到输出变量yi构成的回路，当其他回路均开环时，由uj到yi的传递函数为gij；当其他回路均闭环时，由于其他回路的耦合作用，从uj到yi的传递函数变化过程如下：

受控变量u和输出变量y可以表示为

(3)

(4)

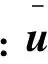
联立(3)、(4)两式可得

(5)

化简可得

(6)

式中I表示单位矩阵。

由上分析，当考虑其他回路的相互作用后，从uj到yi的传递函数为

(7)

例如，对于一个两条回路存在相互作用的两输入两输出系统，如图2所示。

(8)

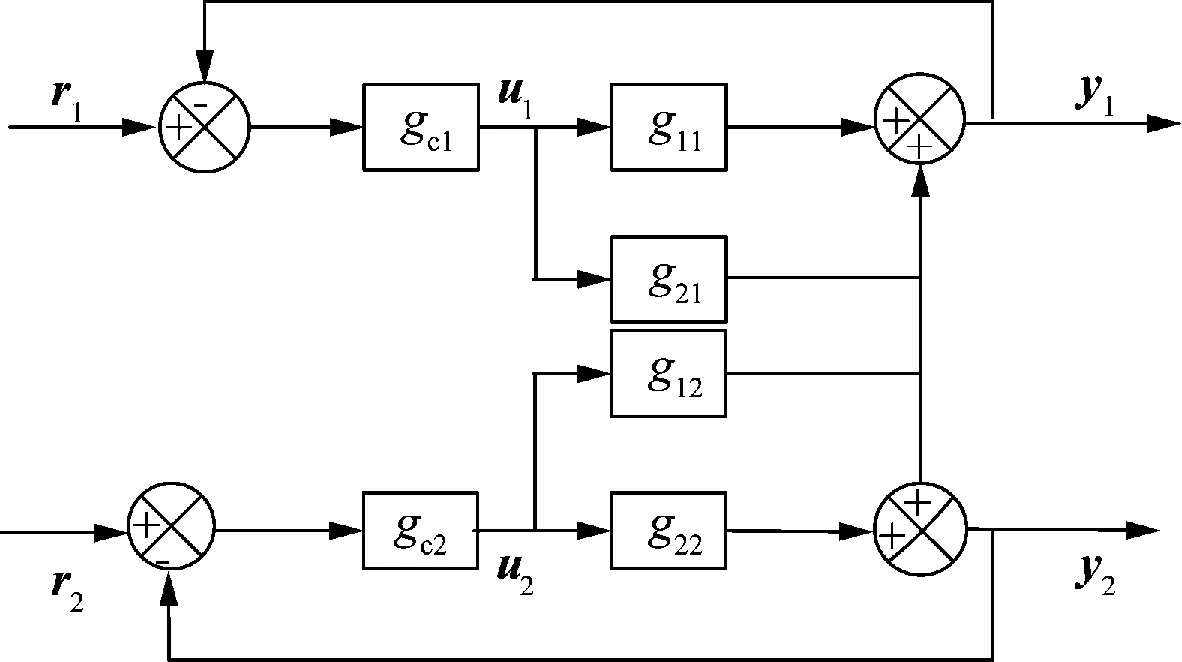
图2 两输入两输出系统

由u1到y1有2条路径，可将两条路径的传递函数通过等效开环过程联系起来[11]，写成y1=G1u1，其中G1=g11-g12g21gc2(1+gc2g22)-1，同理y2=G2u2，G2=g22-g21g12gc1(1+gc1g11)-1，其等效开环环路如图3所示。

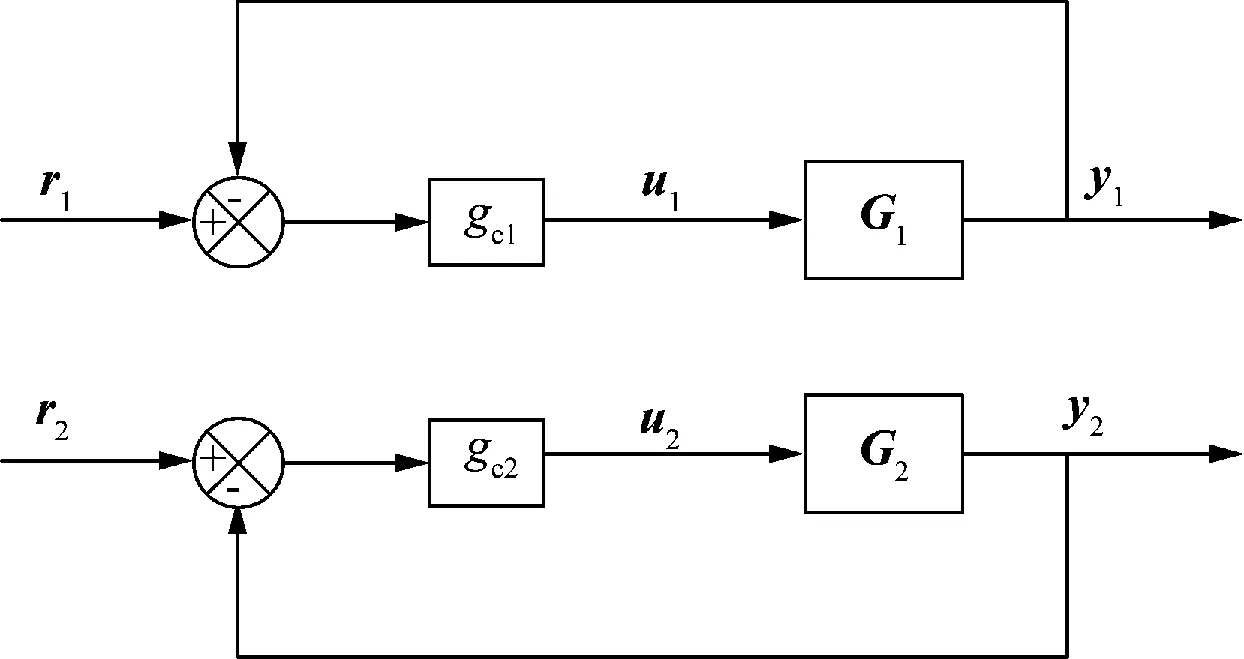
图3 两输入两输出系统等效开环环路

2 基于等效开环过程的附加阻尼协调控制鲁棒稳定性

2.1 小增益定理

稳定性是指当一个系统原来处于一个平衡的状态时，如果受到外界扰动的影响，经过一个过渡过程后，系统仍然能够回到原来的平衡状态。针对线性系统由频域描述的不确定性反馈控制，小增益定理给出系统鲁棒稳定性的充分必要条件[12]。

对如图4所示系统，M(s)为原稳定系统，Δ(s)为未知扰动。

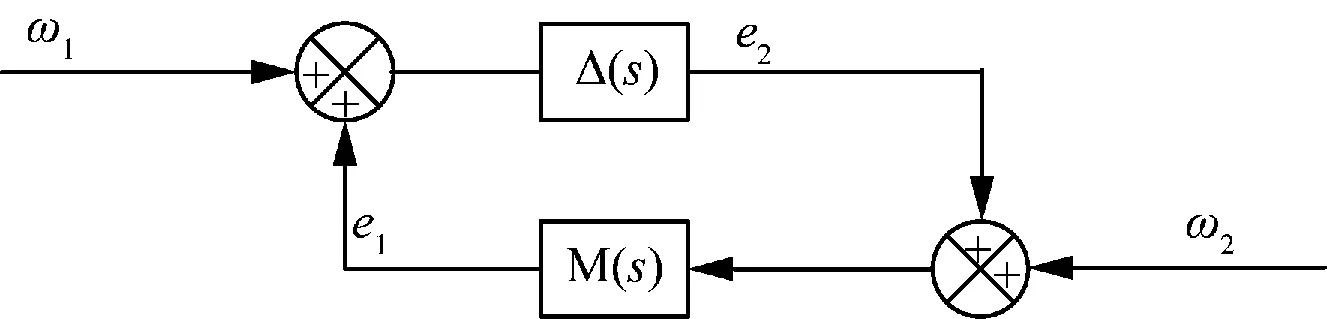
图4 反馈控制系统

小增益定理：设未知扰动有界且满足‖Δs‖≤1，则该系统对于任意Δ(s)是鲁棒稳定的充分必要条件是‖M(s)‖<1。

2.2 基于等效开环过程的VSC-HVDC附加阻尼协调控制分解

与上述针对经典反馈控制等效开环过程理论有所不同，在包含VSC-HVDC的交直流系统中，常见的附加阻尼控制形式如图5所示[13]。

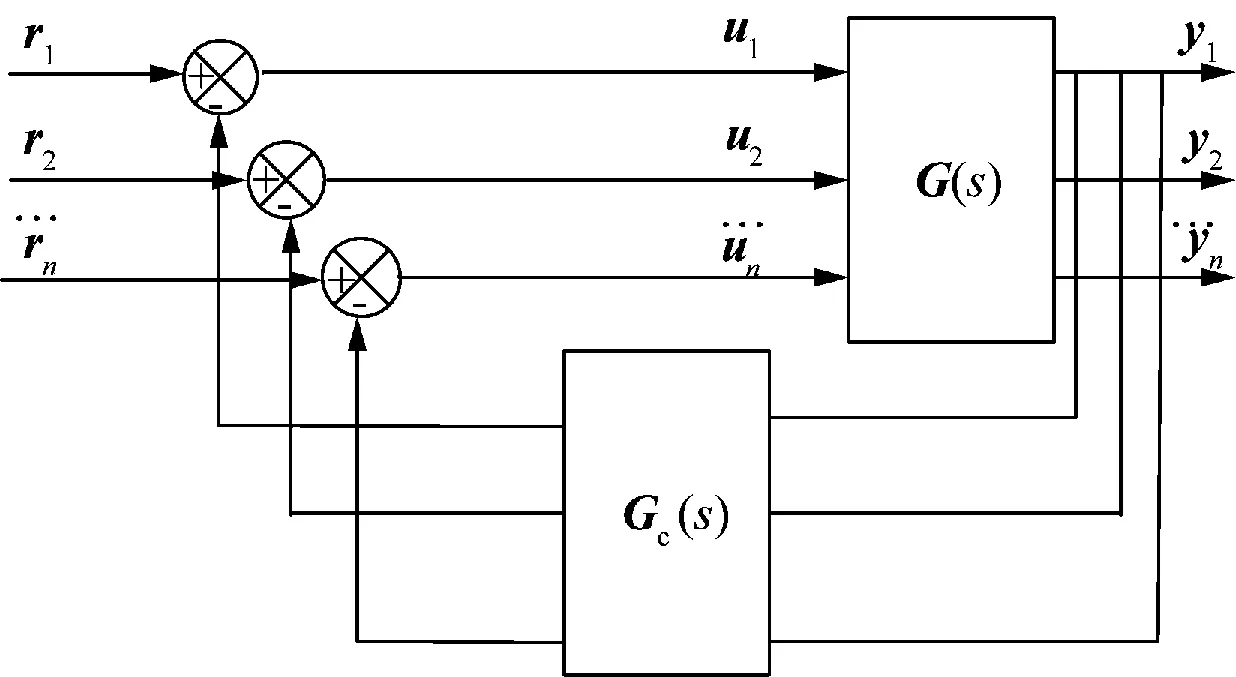
图5 多输入多输出附加阻尼控制系统

研究交直流系统中附加阻尼控制器之间协调控制需要建立新的等效开环过程模型，任意阻尼控制器gci。

(9)

化简可得

(10)

由上可知，考虑其他回路间耦合作用后，从ui到yi的传递函数为

(11)

2.3 发电机PSS与VSC-HVDC附加阻尼控制器协调控制的鲁棒稳定性指标

结合交直流系统附加阻尼控制等效开环过程模型和小增益定理，提出判断发电机PSS和VSC-HVDC附加阻尼控制器间协调控制鲁棒稳定性指标[14]。

基于2.2节对交直流系统的附加阻尼控制器协调控制建立的等效开环过程模型，对于附加阻尼控制器gci，其他控制器与gci的相互作用如图6所示

图6 某回路等效开环过程模型

基于图4小增益定理描述的结构形式，可将图6结构描述为如图7所示的结构形式。

图7 小增益定理M(s)-Δ(s)结构

当其余任意控制器投入或切除时，造成Δ(s)的未知摄动，则M(s)为

(12)

则在第i台附加阻尼控制器以及其他附加阻尼控制器全部投入系统的情形下，系统保持鲁棒稳定的充分必要条件为

‖M(s)‖=

(13)

上式表示在整个控制系统中第i台控制器对整个控制系统的影响，当投入或切除第i台控制器时，若‖M(s)‖<1则表示第i台附加阻尼控制器和其余的附加阻尼控制器间相互作用比较小，在控制器全部投入的情形下，第i台控制器投入或切除后系统仍能保持鲁棒稳定；相反，若‖M(s)‖≥1则表示第i台附加阻尼控制器和其余的附加阻尼控制器间相互作用比较大，在控制器全部投入的情形下，第i台控制器投入或切除后系统不能保持鲁棒稳定。

因此，对于多控制系统，定义鲁棒稳定性指标为

Hij=max{‖Mij(s)‖,‖Mji(s)‖}

(14)

式中

‖Mij(s)‖

(15)

表示在第i台附加阻尼控制器投入的情形下，它对系统其余正在运行的附加阻尼控制器的作用。

‖Mji(s)‖

(16)

表示在第i台附加阻尼控制器投入的情形下，系统其余附加阻尼控制器对它的作用。

当Hij>1时，表示第i台附加阻尼控制器在系统中和其他附加阻尼控制器之间相互作用比较大，系统不能保持鲁棒稳定；当Hij<1时，表示第i台附加阻尼控制器在系统中和其他附加阻尼控制器之间相互作用比较小，系统能够保持鲁棒稳定。

3 含VSC-HVDC的交直流系统振荡模态分析及控制器设计

对于包含VSC-HVDC的交直流系统附加阻尼控制器间的协调控制，一般考虑发电机PSS附加控制器和直流附加控制器间的协调，其控制结构如图8所示。

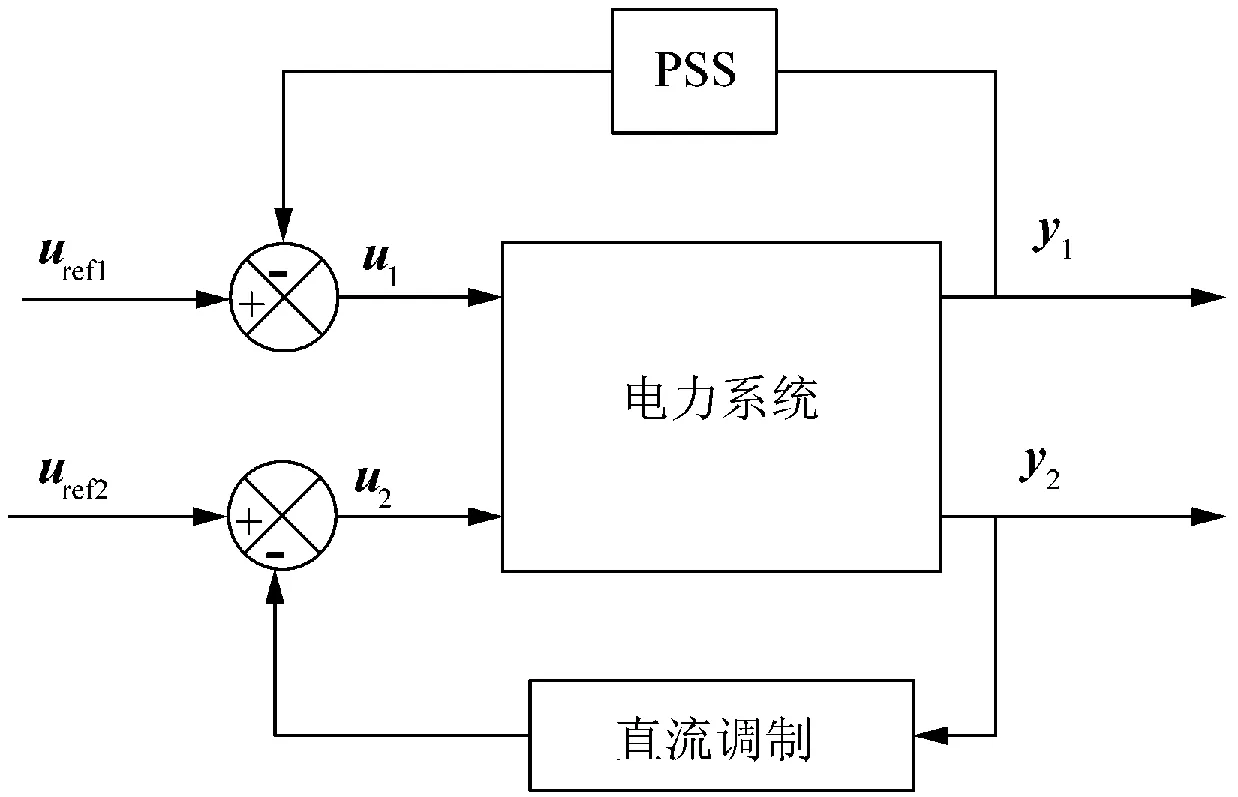
图8 PSS和直流调制回路

图9所示为包含VSC-HVDC的交直流四机两区域系统。所有发电机均装有调速器，4台发电机都采用IEEE-DC1A型直流励磁机自励磁，未安装PSS。交流系统主要参数见文献[15]。从系统左侧往系统右侧传输的功率为600 MW，其中交流线路传输功率为400 MW，含VSC的直流输电系统传输功率为200 MW。整流站VSC1的控制方式为定有功功率控制(Ps1ref=200 MW)和定无功功率控制(Qs1ref=120 MV·A);逆变站VSC2的控制方式为定直流电压(Us2ref=320 kV)控制和定无功功率(Qs2ref=120 MV·A)。

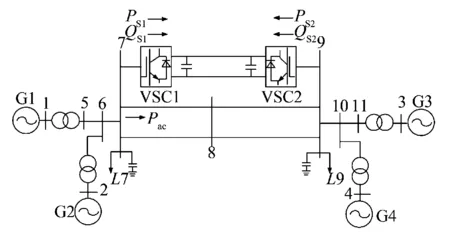
图9 包含VSC-HVDC的交直流四机两区域系统

对图9所示的包含VSC-HVDC的交直流四机两区域系统整流侧施加小扰动激励作为输入，取交流联络线传输有功功率作为输出，采用最小二乘-旋转不变方法(TLS-ESPRIT)辨识算法，得到系统的振荡频率、振荡幅值、阻尼比和振型如表1所示

表1 系统主振荡模态

Table 1 Main oscillation mode of system

由表1可知，系统存在频率为0.450 0 Hz，阻尼比为2.69%的弱阻尼区域间低频振荡模态。对于该主要振荡模态，取图9所示系统中交流母线7和交流母线9间的交流线路有功功率作为VSC-HVDC附加阻尼控制器的控制变量；由于发电机G1和发电机G3

位于不同的区域，故可取三者之间的转速差作为发电机G1处PSS附加阻尼控制器的控制变量，以实现机网协调。可将系统振荡特性写成如下形式

(17)

式中：Δω13表示发电机1、3的转速差；ΔPline表示线路传输功率。

在发电机G1处加小扰动激励作为输入信号，分别以发电机G1和G3转速差和交流联络线有功功率作为输出信号，采用TLS-ESPRIT辨识算法，得到传递函数：

(18)

(19)

在整流侧加小扰动激励作为输入信号，分别以发电机G1和G3转速差和交流联络线有功功率作为输出信号，采用TLS-ESPRIT辨识算法，得到传递函数：

(20)

(21)

根据辨识出的传递函数g11(s)，基于线性二次型最优控制(linear quodratic regulator, LQR)理论设计出PSS附加阻尼控制器gc1(s)为

(22)

根据辨识出的传递函数g22(s)，基于极点配置法设计出直流附加控制器gc2(s)为

(23)

由式(14)可计算出当控制器gc1(s)和控制器gc2(s)共同控制时，该系统的鲁棒稳定性指标Hij为1.517，说明此时系统不能保持鲁棒稳定。

为对比分析，再根据传函g11(s)，基于LQR最优控制理论设计出PSS附加阻尼控制器gc3(s)为

(24)

由式(14)可计算出当控制器gc3(s)和控制器gc2(s)共同控制时，该系统的鲁棒稳定性指标Hij为0.635，说明此时系统能保持鲁棒稳定。

4 仿真验证

4.1 有效性验证

对图9所示含VSC-HVDC的交直流系统，为验证所设计的3个附加阻尼控制器的动态性能，待系统稳定后加入控制器，对测试系统进行短路仿真。具体情况为系统稳定后，在15 s时使系统交流联络线中点发生严重三相接地短路故障，故障持续时间为0.1 s。3个附加阻尼控制器分别对发电机G1和发电机G3间的转速差以及对母线7和母线9间的交流联络线的有功功率控制效果如图10所示。

图10仿真结果表明，在发生严重故障时，设计的控制器gc1(s)、gc2(s)、gc3(s)分别对各自控制的发电机G1和发电机G3间的转速差以及对母线7和母线9间的交流联络线有功功率，有比较有效的控制效果。

4.2 发电机PPS和VSC-HVDC附加阻尼控制器间协调控制鲁棒稳定性验证

为验证上述理论分析结果，分别将2个控制器同时投入系统，在15 s时使系统交流联络线中点发生严重三相接地短路故障，故障持续时间为0.1 s。gc1(s)和gc2(s)同时控制时，系统发电机G1和发电机G3间的转速差以及母线7和母线9间的交流联络线有功功率控制效果如图11所示。gc3(s)和gc2(s)同时控制时，系统发电机G1和发电机G3间的转速差以及母线7和母线9间的交流联络线有功功率控制效果如图11所示。

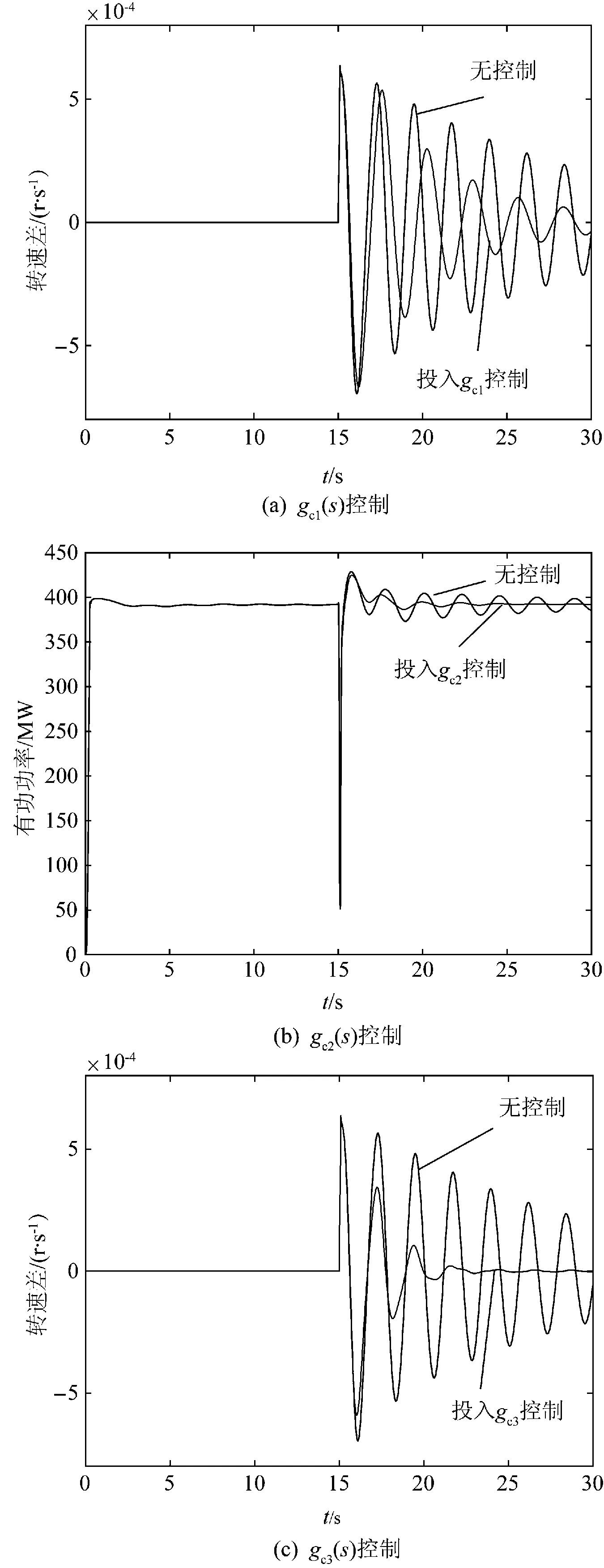
图10 各控制器独立控制效果

由图11可知，当控制器gc1(s)和gc2(s)同时投入系统控制时，发电机G1和G3转速差和交流联络线功率持续振荡不稳定；当控制器gc3(s)和gc2(s)同时投入系统控制时，发电机G1和G3转速差和交流联络线功率经过短暂振荡过程后快速趋于稳定。仿真结果验证了上述理论分析：当控制器gc1(s)和gc2(s)同时投入系统控制时鲁棒稳定指标Hij为1.517，说明系统不能保持鲁棒稳定。当控制器gc3(s)和gc2(s)同时投入系统控制时，鲁棒稳定指标Hij为0.635，说明系统能保持鲁棒稳定。

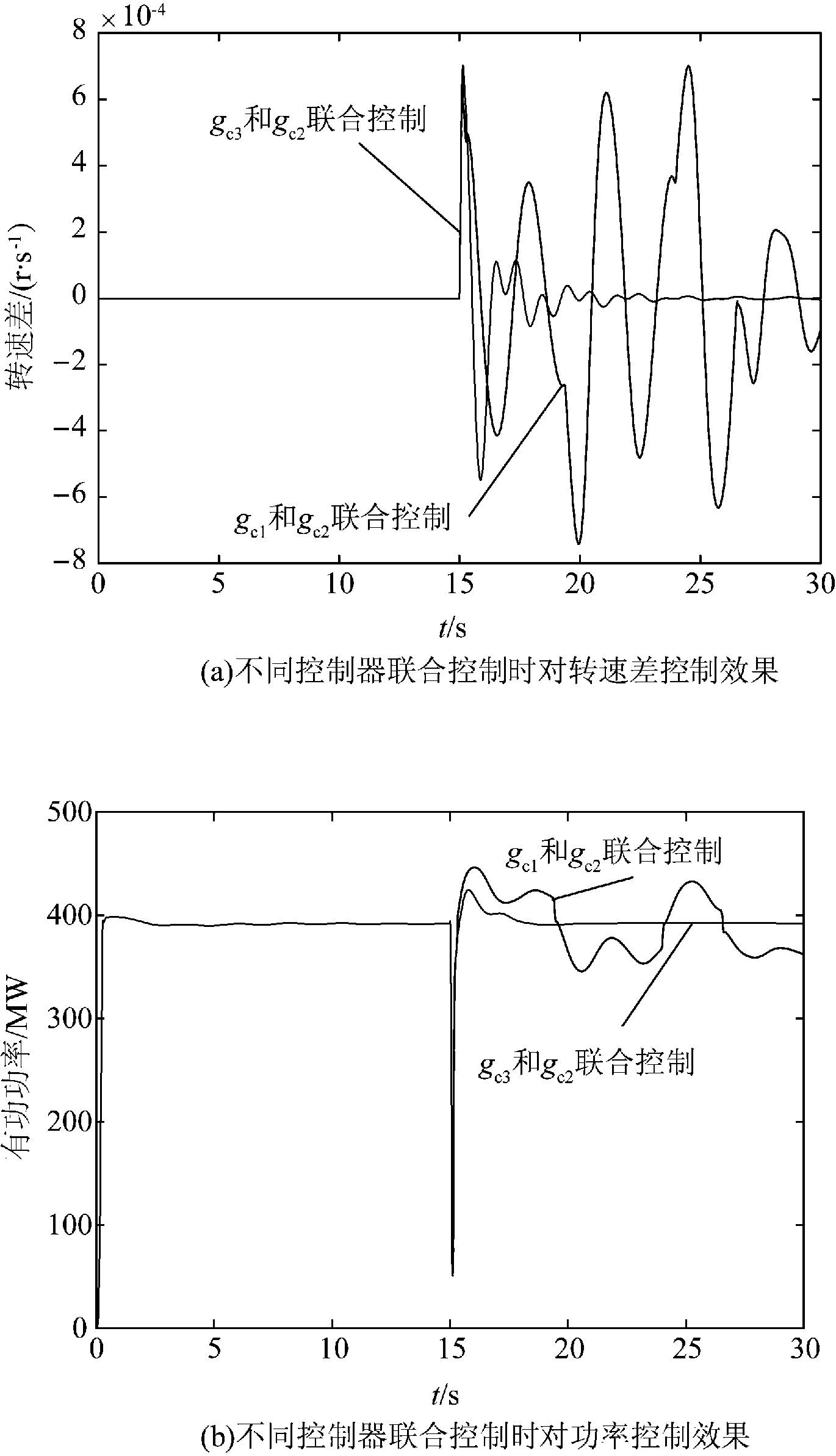
图11 不同控制器联合控制效果

5 结 论

本文针对包含VSC-HVDC的交直流系统中发电机PSS附加阻尼控制和直流附加阻尼控制的协调问题提出了控制器间协调控制鲁棒稳定性量化指标，能够判断发电机PSS和VSC-HVDC附加阻尼控制器之间的协调稳定性。并且设计了能够协调运行且抑制系统低频振荡的发电机PSS附加阻尼控制器和VSC-HVDC附加阻尼控制器，在PSCAD/EMTDC中搭建包含VSC-HVDC的交直流系统进行仿真验证，结果表明所设计控制器和所提指标的有效性。

[1]文俊,张一工,韩民晓,等. 轻型直流输电：一种新一代的HVDC技术[J]. 电网技术, 2003, 27(1):47-51. WEN Jun，ZHANG Yigong，HAN Minxiao，et al.HVDC based on voltage source converter-a new generation of HVDC technique[J].Power System Technology，2003，27(1)：47-51.

[2]包宗贤, 邹超. 向无源网络供电的VSC-HVDC系统的新型控制器设计[J]. 电力系统保护与控制, 2008, 36(14):22-27. BAO Zongxian, ZOU Chao. New control design for VSC-HVDC supplying passive networks[J]. Power system Protection and Control, 2008, 36(14): 22-27.

[3]李永坚, 周有庆, 宋强. 轻型直流输电(HVDC Light)技术的发展与应用[J]. 高电压技术, 2003, 29(10):26-28. LI Yongjian，ZHOU Youqing，SONG Qiang.The development and application of HVDC light technology[J].High Voltage Engineering，2003，29(10)：26-28.

[4] NAYAK N， ROUTRAY S K， ROUT P K. A robust control strategies to improve transient stability in VSC-HVDC based interconnected power systems[C]//Proceedings of the 2011 International Conference on Energy ， Automation， and Signal(ICEAS). Bhubaneswar， Odisha：IEEE， 2011： 1-8.

[5]PREECE R， MILANOVIC J V， ALMUTAIRI A M， et al. Damping of inter-area oscillations in mixed AC/DC networks using WAMS based supplementary controller[J].IEEE Transactions on Power Systems，2013， 28(2)： 1160-1169.

[6]陈蔓,陆继明,毛承雄,等. 一种利用VSC-HVDC提高发电机阻尼的新控制策略[J]. 电网技术,2006,30(9):62-67. CHEN Man， LU Jiming， MAO Chengxiong， et al. A new control strategy using VSC-HVDC to improve generator damping[J]. Power System Technology， 2006， 30(9)： 62-66.

[7]胡兆庆,毛承雄,陆继明. 一种新的优化协调控制在轻型直流输电中的应用[J]. 中国电机工程学报,2005,25(8):41-49. HU Zhaoqing，MAO Chengxiong，LU Jiming.Application of a novel optimal coordinated control to HVDC light[J].Proceedings of the CSEE，2005，25(8)：41-49.

[8]李国杰,马锋. PSS与VSC-HVDC附加阻尼控制器参数协调优化设计[J]. 电网技术,2009,33(11):39-43. LI Guojie，MA Feng.A coordinated tuning algorithm for power system stabilizer and supplementary damping controller of VSC-HVDC transmission system[J]. Power System Technology， 2009， 33(11)：39-43.

[9]张英敏,刘凯. 基于同伦变换的VSC-HVDC分散协调鲁棒阻尼控制器设计[J]. 中国电机工程学报. 2016,36(08):2093-2102 ZHANG Yingmin，LIU kai.Design of decentralized robust damping controller for VSC-HVDC transmission system based on homotopic transformation[J] .Proceedings of the CSEE， 2016， 36(8)： 2093-2102.

[10]HUANG H P， JENG J C. Monitoring and assessment of control performance for single loop systems[J]. Industrial & Engineering Chemistry Research， 2002， 41(5)： 1297-1309.

[11]HUANG H P， JENG J C， CHIANG C H， et al. A direct method for multi-loop PI/PID controller design[J]. Journal of Process Control，2003， 13(8)： 769-786.

[12]梅生伟，申铁龙，刘康志.现代鲁棒控制理论与应用[M].北京：清华大学出版社， 2008.

[13]高磊,刘玉田,汤涌,等. 基于多FACTS的网侧阻尼协调控制量化指标研究[J]. 中国电机工程学报,2014,34(31):5633-5641. GAO Lei， LIU Yutian， TANG Yong, et al. Coordinated control and interaction analysis study for multiple FACTS damping controllers based on effective open-loop process theorem[J]. Proceedings of the CSEE， 2014， 34(31)： 5633-5641.

[14]丁媛媛，刘天琪.基于等效解耦过程的交直流协调控制鲁棒稳定性研究[J]. 电网技术,2016,40(7):1951-1956. DING Yuanyuan，LIU Tianqi.Research on coordinated control robust stability index of HVDC and PSS supplementary damping control based on effective open-loop process theorem[J].Power System Technology， 2016, 40(7)：1951-1956.

[15]KUNDUR P， BALU N J， LAUBY M G. Power system stability and control[M]. New York: McGraw-Hill，1994.

(编辑 刘文莹)

Coordinated Control Robust Stability for VSC-HVDC Damping Controller Based on Effective Open-Loop Process Theorem

LI Zhihan, ZHANG Yingmin, LI Xingyuan, DENG Qi

(School of Electrical Engineering and Information, Sichuan University, Chengdu 610065, China)

According to the phenomenon of low frequency oscillation in the AC-DC interconnected system with voltage source converter-high voltage direct current (VSC-HVDC), this paper converts multi-variable system loop matrix equation into many single variable system loop equation, and establishes the independent mathematical models of each circuit, based on multi-variable system effective open-loop process (EOP) theorem. For the potential uncoordinated problem of each loop controller in multi-input multi-output (MIMO) nonlinear system which contains VSC-HVDC, this paper proposes a coordinated control robust stability index of each supplementary damping controller based on small gain theorem and EOP theorem. Then, the power system stabilizer (PSS) supplementary damping controller and VSC-HVDC supplementary damping controller in cooperative operation was designed to restrain low frequency oscillation. Finally, AC/DC four machine two-area system with a VSC-HVDC in PSCAD /EMTDC has been established, and the validity of the proposed indicators and the feasibility of the designed controller have been verified through simulation.

VSC-HVDC; effective open-loop process; small gain theorem; supplementary damping controller; low frequency oscillation

国家电网公司科技项目(SGRIZLKJ[2015]457)

TM 72

A

1000-7229(2016)10-0093-07

10.3969/j.issn.1000-7229.2016.10.013

2016-07-18

李志晗(1994)，男，硕士研究生，主要研究方向为电力系统稳定与控制、高压直流输电；

张英敏(1974)，女，副教授，主要研究方向为高压直流输电、电力系统稳定与控制；

李兴源(1945)，男，教授，博士生导师，主要研究方向为电力系统稳定与控制、高压直流输电、新能源并网方式；

邓旗(1989)，男，硕士研究生，主要研究方向为电力系统稳定与控制、高压直流输电。