基于功率支援分区协调优化的电网可靠性评估

金黎明,周宁,冯丽,卢治燃,赵渊

(1.国网重庆市电力公司，重庆市 400015；2.输配电装备及系统安全与新技术国家重点实验室(重庆大学)，重庆市400044)

基于功率支援分区协调优化的电网可靠性评估

金黎明1,周宁1,冯丽1,卢治燃2,赵渊2

(1.国网重庆市电力公司，重庆市 400015；2.输配电装备及系统安全与新技术国家重点实验室(重庆大学)，重庆市400044)

为缓解电网可靠性评估计算的复杂性，以分区功率支援为纽带，提出了基于功率支援分区协调优化的电网可靠性评估模型。该模型按发电裕度大小确定子区域的协调求解顺序，将子区域间的联络线功率看作子区域边界节点上的等效负载，按协调求解顺序采用最优负荷削减模型，逐次优化各子区域的负荷削减量和对外功率支援能力。相比于常规电网可靠性评估的分区等值技术，分区协调优化模型由于考虑了各子区域的发电裕度和潮流约束关系，并且采用优化模型计算子区域最大等效负载，因而可实现子区域间功率支援能力的有效建模。在保证较高精度的前提下，提高了电网可靠性评估效率。通过IEEE-RTS96测试系统验证了模型的快速性和有效性。

电网可靠性；等效负载；发电裕度；分区协调

0 引 言

电网可靠性评估包括系统状态抽取，系统状态分析和系统可靠性指标计算3个环节[1]。由于电网可靠性评估需对大量系统状态进行系统状态分析，而系统状态分析又涉及潮流和最优负荷削减计算[2-3]，因此电网可靠性评估的计算复杂性成为亟待解决的难题[4-6]。

提高系统状态分析计算效率，成为降低电网可靠性评估计算复杂性的有效思路。目前已提出的方法有利用系统故障前潮流分布推算系统故障后潮流分布、基于神经网络实现系统故障状态辨识和负荷削减快速计算、采用潮流并行计算技术等[7-10]。这些方法从一定程度上加快了系统状态分析过程，但由于是将电网看成一个统一整体进行分析计算，当电网规模很大时，其效果依然有限。

为提高电网的系统状态分析效率，采用等值技术对电网进行分区等值也是一个有效思路。文献[11-16]研究了电网可靠性评估的DC Ward、AC Ward以及充裕度等值模型。文献[11-12]采用等效机组支援概念，将提供功率支援的子区域模拟为以概率表形式表示的等效发电机和负荷；文献[13]与文献[11-12]思路类似，将子区域间的边界支路表达成等效电源或等效负荷，但该方法需要限定N个子区域中第N号子区域与其余N-1个子区域为星型连接，且只考虑其余N-1个子区域对第N号子区域的功率支援，未考虑第N号子区域对其余N-1个子区域的功率支援；文献[14-16]采用Ward静态等值技术，将子区域的外部网络等效为其边界节点上的注入功率和串并联等值支路。

上述等值方法将整个电网划分为待研究的子区域及其外部网络，对外部网络进行等值以简化电网规模，并且只考虑外部网络对研究子区域的功率支援。文献[17]对外部网络提出了包括等效发电机、等效输电线、等效负荷在内的改进等值模型，考虑了待研究子区域和外部网络的相互功率支援，但由于采用网流模型，没有考虑到子区域的潮流方程约束关系。

为了克服现有等值技术的不足，在前期研究基础上[4,18-19]，提出一种同时考虑子区域间潮流约束关系和彼此功率支援的电网可靠性评估分区协调求解模型。该模型按发电裕度大小确定子区域的协调求解顺序，将子区域间的联络线功率看作子区域边界节点上的等效负载，按协调求解顺序采用基于潮流方程的最优负荷削减模型，逐次求解各子区域的最优负荷削减量和对外功率支援能力。通过上述过程，该模型能够将网络动态等值和子区域最优负荷削减有效结合，基于分区协调思想求解出各子区域和全网的可靠性指标。相比于常规电网可靠性评估的分区等值技术，所提出的分区协调求解模型由于考虑了各子区域的发电裕度和潮流约束关系，并且采用优化模型计算子区域最大等效负载，因而可实现子区域间功率支援能力的有效建模。

电网可靠性评估的分区协调求解意味着将一个统一整体的电网分解成多个子区域协调求解，也意味着丢失完整电网的部分运行信息。因此，分区可靠性评估相对于完整电网可靠性评估而言，计算精度有所下降。但本文提出的分区协调求解模型由于可以对子区域间功率支援能力进行有效建模，因而可以在保证较高精度的前提下，大幅提高可靠性评估效率。通过两区域和三区域IEEE-RTS96可靠性测试系统的可靠性评估，验证所提方法的准确性和有效性。

1 分区协调求解方法的总体思路

电网可靠性分区协调求解的基本步骤如下所述。(1)划分整个电网为若干个子区域。分区时应尽量使各子区域节点数划分均匀，且各子区域在正常情况下自身能满足功率平衡。(2)抽样得到整个电网的系统状态，在每一个系统状态下，按照发电裕度确定子区域的协调求解顺序，对各子区域的最优负荷削减模型进行逐次求解。对于每一个子区域，将该子区域的相邻已求解子区域等值为等效电源或等效负载计入到该子区域的最优负荷削减模型中，求解该子区域的最优负荷削减量及其对相邻未求解子区域的支援功率或吸收功率。(3)记录会削减负荷的系统状态和各子区域的削负荷量，计算系统和各子区域的可靠性指标。

第2步是分区协调求解的重要实施步骤，各子区域可以分为3类：(1)初始子区域，发电裕度为正且最大，最先求解的子区域；(2)中间子区域，有相邻未求解(未进行最优负荷削减模型计算)子区域的子区域，已知与其相邻的各个已求解子区域对其支援或从其吸收的功率；(3)末端子区域，无相邻未求解子区域的子区域，已知与其相邻的各子区域对其支援或从其吸收的功率。

通过各子区域独立优化和网络动态等值，可以实现分区协调求解，具体求解过程为：(1)将初始子区域对相邻子区域的功率支援能力看成等效负载，采用最优负荷削减模型计算初始子区域的最优负荷削减及其与相邻子区域相连边界节点的最大等效负载；(2)将已求解子区域与中间子区域相连边界节点的等效负载作为中间子区域的等效电源，中间子区域对相邻未求解子区域的功率支援(或需求)视为等效负载，采用最优负荷削减模型计算中间子区域的最优负荷削减，及其与相邻未求解子区域相连边界节点的最大等效负载；(3)将已求解子区域与末端子区域相连边界节点的等效负载作为末端子区域的等效电源，采用传统可靠性评估中的最优负荷削减模型，计算其最优负荷削减(注意孤立子区域也属于末端子区域，对于孤立子区域，直接采用传统可靠性评估中的最优负荷削减模型计算其负荷削减)。

图1为三分区协调计算示意图。采用图1的8节点网络为例简要说明上述概念，该网络中线路容量都为40 MW。将网络从线路L2和线路L6处划分为3个子区域，如图1(a)所示。抽取系统状态，例如抽取到的系统状态为节点3上发电机G3故障，节点8上发电机G6故障，其他元件(包括发电机和线路)正常运行，可见子区域A，B和C的发电裕度分别为20 MW，-10 MW和-15 MW。根据协调求解原理，第1步将子区域A作为初始子区域，将子区域A对子区域B的功率支援视为等效负载，消去子区域B和C，从图1(a)可知子区域A在不违背运行约束的情况下能满足自身负荷需求，且边界节点2上可接入20 MW的最大等效负载，即子区域A最大对外支援能力为20 MW。第2步求解子区域B，可见子区域B是中间子区域，将已求解子区域A的等效负载 20 MW作为等效电源接入子区域B，将子区域B对子区域C的功率支援视为等效负载，消去子区域A和C，可见子区域B不会发生负荷削减，且边界节点6上可接入10 MW最大等效负载，即子区域B对外最大功率支援能力为10 MW。第3步求解子区域C，可见子区域C为末端子区域，将已求解子区域B与子区域C相连边界节点(节点6)的等效负载10 MW作为等效电源接入子区域C，可见子区域C会失去负荷5 MW。通过以上3步的分区协调计算可知，该系统状态下全网会削减5 MW负荷。最后，对抽取到的所有系统状态的分析结果进行统计，即可计算全网和各子区域的可靠性指标。

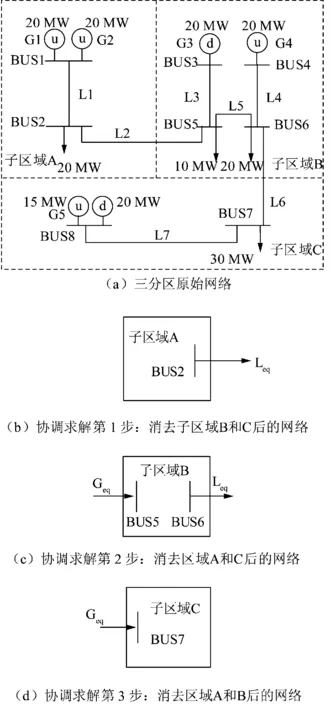
图1 三分区协调计算示意图

对于图1所示网络，系统期望电量不足指标可以按照公式(1)计算。

EEENS=EEENS,A+EEENS,B+EEENS,C

(1)

式中EEENS,A、EEENS,B和EEENS,C分别为子区域A、子区域B和子区域C的期望电量不足指标， MW·h·a-1。

系统期望失负荷概率为

(2)

式中：Nf为全网发生负荷削减的系统状态总数，若三区域中任一区域发生负荷削减，则视为全网发生一次负荷削减；N为抽取的系统状态总数。

以子区域A为例，子区域A的期望电量不足为

(3)

式中LC,A(s)为系统状态s下子区域A的负荷削减量， MW。

子区域A的期望失负荷概率指标计算公式为

(4)

式中Nf,A为子区域A发生失负荷的次数。

2 分区协调求解顺序的确定及子区域对外支援能力的建模

2.1 分区协调求解顺序

本文按发电裕度的大小确定各子区域的逐次协调求解顺序。发电裕度定义为子区域可用发电容量与负荷需求之差。当子区域k无解列情况，即子区域k是一个联通的网络时，子区域k的发电裕度为

ΔPk=Gk-Lk

(5)

式中：Gk和Lk分别为子区域k的可用发电容量和负荷。

如果子区域k因线路故障导致其解列成m个孤立子网，且其中有n个子网包含了与其他子区域相连的边界节点，则第j个子网的发电裕度用ΔPkj表示，而对于不含边界节点的子网，由于与其他子区域无功率交换，因此无须计算发电裕度。ΔPkj由子网j中可用发电机容量减去负荷得到。在系统状态s下，将子区域k的发电裕度定义为含边界节点的解列子网中发电裕度的最大值。

(6)

对于含多个子区域的系统而言，在系统状态s下，确定协调求解顺序是不断确定当前求解子区域(要进行最优负荷削减模型，计算的子区域)和更新待求解子区域集的过程，具体过程如下详述。

(1)采用式(5)—(6)计算各子区域发电裕度的初始值，选择发电裕度为正且数值最大的子区域作为初始子区域。将初始子区域作为当前求解子区域。

(2)如果当前求解子区域是初始子区域，转步骤(3)；否则，将已求解子区域与当前求解子区域相连边界节点的等效负载作为等效电源接入当前求解子区域，转步骤(3)。

(3)如果当前求解子区域是末端子区域，采用传统可靠性评估中的最优负荷削减模型计算其最优负荷削减量；如果当前求解子区域是初始子区域或中间子区域，基于本文2.2节中提出的最优负荷削减模型，计算当前求解子区域的最优负荷削减量及最大等效负载，将等效负载作为其相邻未求解子区域的等效电源，更新其相邻未求解子区域的发电裕度，并将所有相邻未求解子区域并入待求解子区域集。

(4)如果所有子区域都已进行过最优负荷削减计算，转步骤(5)；否则，将待求解子区域集之中发电裕度最大的子区域作为当前求解子区域并从待求解子区域集中剔除，返回步骤(3)。

(5)算法结束，记录各子区域的失负荷量。

从上述步骤可以看出，在系统状态s下，协调求解顺序的确定和子区域的最优负荷削减计算是同时推进的，对当前求解子区域的最优负荷削减模型进行计算，更新待求解子区域集，并确定下一个要求解的子区域。

图2是一个四区域网络的示意图，各圆圈代表子区域，圆圈之间的连接线代表各子区域之间的邻接关系。以图2为例说明协调求解顺序的确定过程。

图2 四区域网络示意图

假设子区域1是初始子区域，基于最优负荷削减模型求解其最优负荷削减及最大等效负载，将等效负载作为相邻未求解子区域2和3的等效电源，更新子区域2和3的发电裕度，将子区域2和3并入待求解子区域集。假设在待求解子区域集{2，3}中子区域2的发电裕度最大，将子区域2作为求解子区域并从待求解子区域集中剔除，可见子区域2是中间子区域，将子区域1与子区域2相连边界节点上的等效负载作为等效电源接入子区域2，基于最优负荷削减模型求解出子区域2的最优负荷削减及最大等效负载，将等效负载作为相邻未求解子区域3和4的等效电源，更新子区域3和4的发电裕度，将子区域3和4并入待求解子区域集。假设在待求解子区域集{3，4}中子区域3的发电裕度最大，将子区域3作为求解子区域并从待求解子区域集中剔除，由于子区域3是末端子区域，只需用传统最优削减负荷模型计算其最优负荷削减。最后用传统最优削减负荷模型计算末端子区域4的最优负荷削减。

2.2 基于最优负荷削减的对外支援能力建模

对于当前求解子区域，在进行最优负荷削减计算之前先判断其类型。如果当前求解子区域是末端子区域，采用传统可靠性评估中的最优负荷削减模型计算其最优负荷削减量；如果当前求解子区域是初始子区域，将其对相邻子区域的功率支援看成等效负载，采用本节提出的最优负荷削减模型计算其最优负荷削减量及边界节点上的最大等效负载；如果当前求解子区域是中间子区域，将已求解子区域与当前求解子区域相连边界节点上的等效负载看成等效电源接入当前求解子区域，将当前求解子区域对其相邻未求解子区域的功率支援(或需求)视为等效负载，采用本节所提出的最优负荷削减模型计算当前求解子区域的最优负荷削减量，及其与相邻未求解子区域相连边界节点上的最大等效负载。

子区域k边界节点(边界节点指的是子区域k与相邻未求解子区域相连的边界节点)的最大等效负载受该子区域元件随机故障、网络拓扑、运行约束等因素共同影响，是由子区域k的元件状态和联络线状态共同决定的随机变量。在某一系统状态s下，子区域k边界节点的最大等效负载可以理解为该子区域在满足自身负荷的前提下对外供电的最大能力，也可以理解为该子区域在边界节点上有功出力(即该子区域对相邻未求解子区域的功率支援，或者说是该子区域边界节点上的等效负载)的上限。求解子区域最优负荷削减和最大负载能力的优化模型如式(7)—(14)所示，其目标函数表示在子区域负荷削减最小的情况下尽量使得边界节点等效负载最大。

(7)

s.t.

(8)

(9)

(10)

(11)

(12)

(13)

(14)

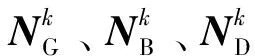
由式(13)可以看出，已求解子区域在与子区域k相邻边界节点上的有功出力的上限值是该已求解子区域在与子区域k相邻边界节点上的最大等效负载。求解出子区域k边界节点上的最大等效负载以后，该最大等效负载又将作为子区域k在与相邻未求解子区域相连边界节点上有功出力的上限，存在于子区域k相邻未求解子区域的最优负荷削减模型的约束条件中。

电网各子区域间不希望出现功率环流，且子区域k对外的实际功率支援不能超过边界节点所连联络线的输电容量。基于以上两点，对最大等效负载计算模型增加如式(15)所示的限制条件，等效负载的正负由子区域k的发电裕度确定。

(15)

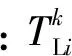
(16)

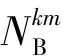
(17)

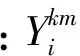
3 可靠性评估分区协调求解算法

本文采取非序贯蒙特卡洛仿真[21-22]抽取系统状态s，主要流程如图3所示，本文的可靠性评估分区协调求解算法与传统方法的主要区别为：(1)对系统故障状态采用分区协调方法计算各子区域最优负荷削减量；(2)可靠性指标统计公式不同。对于含有多个子区域的系统，可靠性评估的分区协调计算步骤如下详述。

(1)采用非序贯蒙特卡洛仿真进行随机抽样，得到系统状态。

(2)判断全网是否出现运行约束违背现象，如果否，则转步骤(1)；如果是，则转步骤(3)。

(3)采用式(5)—(6)计算各子区域发电裕度的初始值，若子区域发生解列，计算子网的发电裕度，将最大的子网发电裕度作为该子区域的发电裕度。

(4)判断是否有子区域孤立于其余子区域，若否，转步骤(5)；若是，则对孤立子区域按传统可靠性评估方法计算最优负荷削减量，对剩余的子区域转步骤(5)。

(5)选发电裕度为正且最大的子区域作为初始子区域，将初始子区域作为当前求解子区域。

图3 可靠性评估非序贯蒙特卡洛模拟流程图

(6)如果当前求解子区域是初始子区域，转步骤(7)；否则，将已求解子区域与当前求解子区域相连边界节点的等效负载作为等效电源接入当前求解子区域，转步骤(7)。

(7)如果当前求解子区域是末端子区域，采用传统可靠性评估方法计算其最优负荷削减量；如果当前求解子区域是初始子区域或中间子区域，基于本文在2.2节中提出的最优负荷削减模型计算当前求解子区域的最优负荷削减量及最大等效负载，将等效负载作为其相邻未求解子区域的等效电源，更新其相邻未求解子区域的发电裕度，并将所有相邻未求解子区域并入待求解子区域集。

(8)如果所有子区域都已进行过最优负荷削减计算，转步骤(9)；否则，将待求解子区域集之中发电裕度最大的子区域作为当前求解子区域并从待求解子区域集中剔除，返回步骤(6)。

(9)记录各子区域的负荷削减量，累计可靠性指标并判断是否达到收敛条件，即指标方差系数是否小于阈值或系统状态数是否达到设定抽样次数N。若未达到收敛条件，转步骤(1)；若达到收敛条件，算法结束，统计各子区域和系统的可靠性指标。

上述多区域模型可靠性评估协调分解算法的流程如图4所示。对于含有Nk个子区域的电网而言，全网的期望电量不足指标计算公式为

(18)

式中EEENS,i是第i个子区域的期望电量不足指标。

图4 多区域模型协调分解评估流程图

全网的期望失负荷概率如公式(2)所示，式中Nf为全网发生失负荷的次数，若任一子区域发生负荷削减，视为全网发生失负荷。

4 算例分析

为验证本文方法的有效性并研究不同分区方式对所提方法效果的影响，本文对IEEE-RTS96系统进行了可靠性评估分析。

4.1 两区域RTS96

标准IEEE-RTS96测试系统48节点网络[23]如图5所示。该系统由2个完全相同的IEEE-RTS79系统通过3条联络线相连组成，总装机容量为6 810 MW，总负荷为5 700 MW。图5中联络线上的数值表示线路容量。将2个RTS79网络分别命名为子区域A和子区域B，则RTS96-48节点系统按子区域A、B均分为2个区域。子区域A和子区域B的节点编号用1—24表示。可见，各子区域能满足自身功率平衡，其发电裕度ΔP=5.55 pu(以100 MW为基准值的pu值)。这样均匀分区正好满足本文第1节提出的分区原则，使各子区域有相同的节点数，且自身在正常情况下都能满足功率平衡，有利于提高分区协调求解模型的效率和精度。

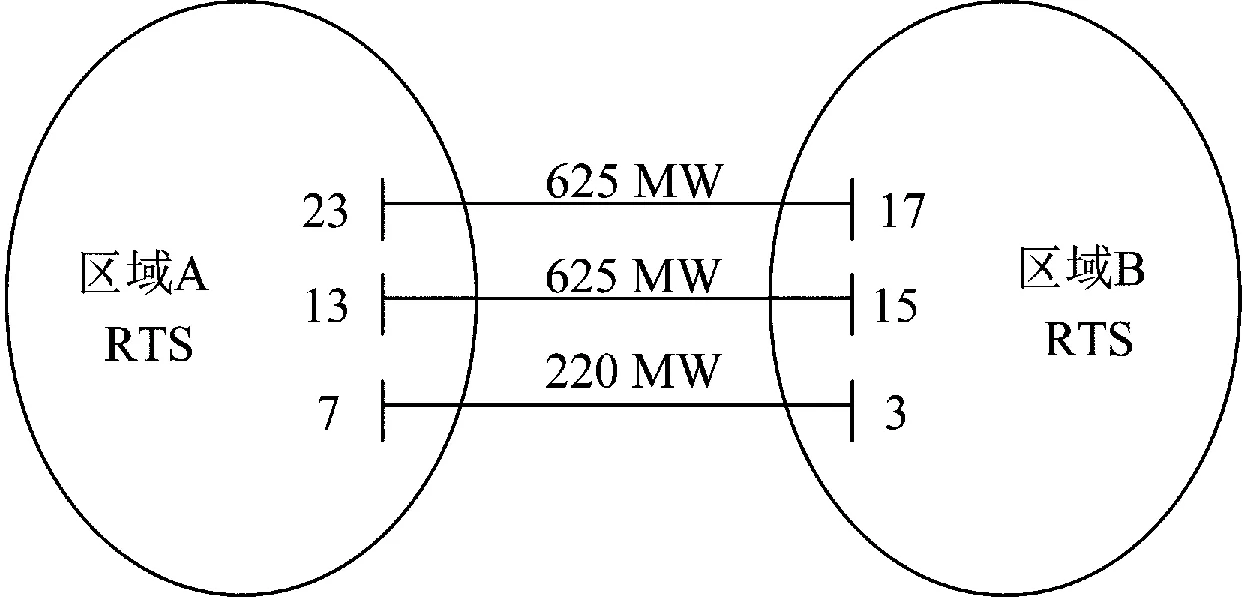
图5 两区域RTS96网络

负荷采用年峰荷模型。考虑到系统故障状态的最优负荷削减分析是可靠性评估中最费时的环节，首先对某系统状态下分区协调求解模型和传统可靠性评估中完整电网分析的分析效率进行对比。表1列

出了某一随机抽取得到的系统故障状态，子区域A有2台发电机故障，子区域B有5台发电机故障。由于子区域A的发电裕度大于子区域B，选取子区域A为初始子区域，子区域B为末端子区域，采用2.2节所述的最优负荷削减模型计算得到子区域A不发生负荷削减，将子区域A边界节点的最大等效负载作为等效电源接入子区域B，采用传统最优负荷削减模型计算出子区域B的负荷削减为37 MW，即全网负荷削减37 MW。

表1 两区域RTS96系统的某故障系统状态

Table 1 A system failure state of two-areas RTS96

表2给出了在该状态下，采用传统可靠性评估方法，对完整电网进行最优负荷削减计算，以及采用分区协调求解进行最优负荷削减计算的对比结果。可见，2种方法得到的负荷削减量相等，且分区协调求解的计算时间是完整电网分析的75%。这表明分区协调求解模型加快了系统状态分析速度，且有较好的计算精度。

表2 两区域RTS96系统某故障系统状态下的负荷削减对比

Table 2 Load curtailment comparison of two-areas RTS96 under system failure state

为了进一步验证本文方法的有效性，分别采用传统可靠性评估方法(完整电网分析)和分区协调求解方法对系统可靠性进行评估。系统状态的抽样方法采用非序贯蒙特卡洛仿真，仿真次数为105次。表3列出了2种方法得到的系统可靠性评估结果。分区协调求解方法得到的评估结果与完整电网分析得到的评估结果非常接近，系统pLOLP指标和EEENS指标的相对误差都在0.1%左右。而采用分解协调求解方法的计算时间约为采用完整电网分析方法的24%，这证明分区协调求解模型通过将大规模电网的计算分析问题转换为2个小规模子问题，有效地提高了计算效率。

表3 两区域RTS96系统可靠性指标对比

Table 3 Reliability evaluation comparison of two-areas RTS96

表4给出了2种方法计算得到的子区域A和B的可靠性指标。采用分区协调求解得到的子区域EEENS指标与完整电网分析相比，相对误差约为7%。因而分区协调求解模型的计算准确性依然较好。

表4 两区域RTS96子区域EEENS指标对比

Table 4EEENSindex comparison of subareas of two-areas RTS96

4.2 三区域RTS96

使用RTS96测试系统的73节点网络，即三区域RTS96系统对本文提出的分区协调求解模型进行说明，如图6所示。该系统由3个完全相同的IEEE-RTS79系统通过5条联络线相连构成。与两区域RTS96系统类似，三区域RTS96系统也采用均匀分区方式，将3个RTS79系统分别命名为子区域A、子区域B和子区域C。在正常运行时，各子区域均能满足自身功率平衡。

图6 三区域RTS96网络

首先对某系统状态下分区协调求解模型和传统可靠性评估中完整电网分析的分析效率进行比较。表5给出了某一故障系统状态。在该系统故障状态下，子区域B的发电裕度最大，因而选取子区域B为初始子区域，采用2.2节所述的最优负荷削减模型计算子区域B的最优负荷削减和最大负载能力，计算得到子区域B不发生负荷削减，将子区域B边界节点3、5和17上的最大等效负载作为等效电源接入子区域A，将子区域B边界节点23上的最大等效负载作为等效电源接入子区域C，更新子区域A和子区域C的发电裕度，由于子区域A的发电裕度大于子区域C，选取子区域A为中间子区域，采用2.2节所述的最优负荷削减模型计算子区域A的最优负荷削减和最大负载能力，将子区域A边界节点21上的最大等效负载作为等效电源接入子区域C(末端子区域)，采用传统最优削负荷模型计算出子区域C的负荷削减量为222 MW。

表5 三区域RTS96某故障系统状态

Table 5 A system failure state of three-areas RTS96

表6为该故障系统状态下采用完整电网分析和分区协调求解得到的结果对比。可见分区协调求解得到的系统负荷削减量与完整电网分析得到的完全一致，且分区协调求解的计算时间约为全网分析的50%。

表6 三区域RTS96系统某故障系统状态下的负荷削减对比

Table 6 Load curtailment comparison of three-areas RTS96 under system failure state

表7为三区域RTS96系统采用分区协调求解模型和传统可靠性评估方法(完整电网分析)计算得到的可靠性指标。与完整电网分析得到的结果相比，由分区协调求解模型得到的失负荷概率和期望缺供电量指标其计算误差均小于1%。而分区协调求解的评估时间却是完整电网分析的5%左右。

表7 三区域RTS96全网可靠性指标对比

Table 7 Reliability index comparison of three-areas RTS96

4.3 分区方式探讨

本文根据各子区域正常运行情况下是否满足功率平衡以及各子区域节点数占全网节点总数的比例，对RTS96-48节点网络的3种分区方式(如表8所示)下的分区协调求解效果进行了比较。

分区方式1：将48节点RTS96均分为2个RTS79系统，即各子区域节点数按1∶1等比例划分，子区域发电裕度ΔP=555 MW，各子区域在正常运行条件下满足自身功率平衡。

分区方式2：各子区域节点数按1∶3的比例划分。子区域I发电裕度ΔPⅠ=-648 MW，在正常运行条件下不能满足自身功率平衡，需要其他子区域向其提供有功功率，对外依赖性较强；子区域II发电裕度ΔPⅡ=1 758 MW。两子区域联络线上功率交换较多。

分区方式3：各子区域节点数按约1∶4的比例划分。子区域Ⅰ发电裕度ΔPⅠ=217 MW，子区域Ⅱ发电裕度为ΔPⅡ=892 MW，正常情况下各子区域均满足功率平衡。

表8 不同分区方式

Table 8 Different ways of network partition

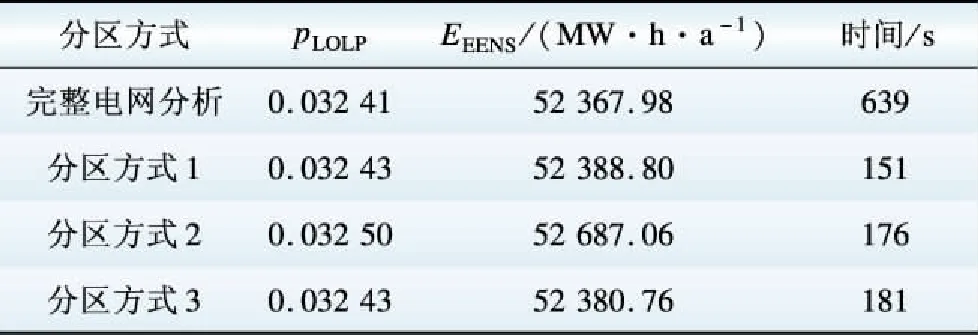
表9列出了不同分区方式下电网可靠性评估结果。由表9可得：(1)从分区方式3，到分区方式2，最后到分区方式1，各子区域节点数划分逐渐均匀，而分区协调求解的可靠性评估时间也逐渐缩短，即子区域节点数划分越平均，计算速度越快；(2)各分区方式的系统EEENS和pLOLP指标均与完整电网分析非常接近，但相比之下，分区方式1和分区方式3具有更高的计算精度，即当划分的子区域正常情况下自身能满足功率平衡时，分区协调求解的可靠性评估结果精度更高。

表9 不同分区方式两区域模型可靠性指标对比

Table 9 Reliability index comparison of two-areas model for different network partition modes

为进一步验证分区协调求解模型的有效性，本文在线路容量取原始值的90%、发电机和负荷取原始值的110% 2种场景下采用3种分区方式对系统可靠性进行评估，评估结果见表10和表11。由表10和表11可得，参数改变后分区协调求解模型的计算误差有所增加，但计算精度仍然较高。以EEENS指标为例，线路容量变为原来的90%时，分区方式3的EEENS指标的计算误差为0.5%，分区方式2为3.2%，而分区方式1为0.7%。发电机和负荷变为原来的110%时，分区方式3的EEENS指标的计算误差为0.4%，分区方式2为2.9%，分区方式1为0.5%。在2种场景下，分区方式1和分区方式3的计算精度都高于分区方式2，这再次说明能够保证各子区域在正常情况下满足功率平衡的分区方式具有更高的可靠性评估精度。从表10和表11的计算时间来看，3种分区方式都能大幅缩短计算时间，其中分区方式1(最均匀的分区方式)所需计算时间最短。综合上述分析结果可知，本文分区协调求解模型能够在保证较高精度的前提下大幅提高计算效率，在具体工程应用中为了使效果更好，应当尽量使子分区的节点数比较均匀以及各子区域在正常情况下能够满足自身功率平衡。

表10 90%线路容量下两区域模型可靠性指标对比

Table 10 Reliability index comparison of two-areas model with 90% line capacity

表11 110%发电机和负荷下两区域模型可靠性指标对比

5 结 论

本文提出一种用于大电网可靠性评估的分区协调求解模型。该模型将电网划分为多个子区域，按照发电裕度确定各子区域的协调求解顺序，将子区域间的联络线视为区域边界节点的等效负载，采用最优负荷削减模型按照协调求解顺序逐次求解子区域彼此间的功率支援和各子区域的最优负荷削减。该模型将子区域动态网络等值和各子区域独立优化相结合，基于分区协调思想求解出各子区域和全网的可靠性指标，不仅能够实现子区域间功率支援的有效建模，而且能够在保证较高精度的前提下大幅提高可靠性评估效率。通过对不同区域划分方式的对比分析，发现各子区域节点数越均匀，分区协调求解的计算时间越短；各子区域在正常情况下能满足自身功率平衡时，分区求解模型的计算精度会更高。

[1]李文沅, 周家启, 卢继平, 等. 电力系统风险评估: 模型, 方法和应用[M]. 北京：科学出版社, 2006.

[2]LI W Y.Risk assessment of power systems：models，methods and applications[M].New Jersey, USA：IEEE Press，2005：1-6.

[3]赵渊, 周家启, 周念成, 等. 大电力系统可靠性评估的解析计算模型[J]. 中国电机工程学报, 2006, 26(5): 19-25. ZHAO Yuan, ZHOU Jiaqi, ZHOU Niancheng, et al. An analytical approach for bulk power systems reliability assessment[J]. Proceedings of the CSEE, 2006, 26(5): 19-25.

[4]卢治燃.大电网可靠性评估的外网概率等值和分区协调求解模型研究[D]. 重庆：重庆大学, 2015. LU Zhiran. Research on probability equivalent and network partition coordination model for power system reliability evaluation[D]. Chongqing: Chongqing University, 2015.

[5]赵渊, 周家启, 谢开贵. 基于网流规划的发输电组合系统可靠性评估模型研究[J]. 电网技术, 2003, 27(10): 21-24. ZHAO Yuan, ZHOU Jiaqi, XIE Kaigui. Study on reliability assessment model of composite generation and transmission system based on network flow programming[J]. Power System Technology, 2003,27(10): 21-24.

[6]AKHAVEIN A, FIRUZABAD M F, BILLINTONR, et al. Review of reduction techniques in the determination of composite system adequacy equivalents[J]. Electric Power Systems Research, 2010, 80(12): 1385-1393.

[7]熊宁, 蔡恒, 程虹. 支路故障后静态电压稳定裕度的估算[J]. 电网技术, 2012, 36(9): 151-154. XIONG Ning, CAI Heng, CHENG Hong. A method to estimate static voltage stability margin after branch outage[J]. Power System Technology, 2012, 36(9): 151-154.

[8]吴开贵, 王韶, 张安邦, 等. 基于RBF神经网络的电网可靠性评估模型研究[J]. 中国电机工程学报, 2000, 20(6):9-12. WU Kaigui, WANG Shao, ZHANG Anbang, et al. The study on reliability assessment of electrical power systems using RBF neural network[J]. Proceedings of the CSEE, 2000, 20(6):9-12.

[9]谢开贵, 周家启. 基于ANN削减负荷的发输电组合系统可靠性评估[J]. 电力系统自动化, 2002, 26(22): 31-33, 44. XIE Kaigui, ZHOU Jiaqi. Reliability evaluation of bulk power system using artificial neural network for load shedding[J]. Automation of Electric Power Systems, 2002, 26(22): 31-33, 44.

[10]胡博, 谢开贵, 赵渊, 等. 电力系统可靠性评估的动态任务分配并行算法[J]. 电力系统自动化, 2011, 35(10): 35-41. HU Bo, XIE Kaigui, ZHAO Yuan, et al. Parallel algorithm for reliability evaluation of bulk power system with dynamic task allocation technique[J]. Automation of Electric Power Systems, 2011, 35(10): 35-41.

[11]ZHANG W, BILLINTON R. Application of an adequacy equivalent method in bulk power system reliability evaluation[J]. IEEE Transactions on Power Systems, 1998, 13(2): 661-666.

[12]BILLINTON R, ZHANG W. Adequacy equivalent development of composite generation and transmission systems[J]. Reliability Engineering & System Safety, 2001, 74(1): 1-12.

[13]孙闻,方华亮,余锦河,等.基于分区的大电网可靠性计算[J]. 华中科技大学学报(自然科学版),2013,41(4):88-92. SUN Wen, FANG Hualiang, YU Jinhe, et al. Computing the reliability of large-scale power grids by partitioning[J]. Journal of Huangzhong University of Science & Technology (Natural Science Edition), 2013, 41(4): 88-92.

[14]AUDOMVONGSEREE K, EUA-ARPORN B. Composite system reliability evaluation using AC equivalent network[C]//International Conference on Power System Technology, 2000. IEEE, 2000: 751-756.

[15]MAGHRABY H A M, ALLAN R N. Application of DC equivalents to the reliability evaluation of composite power systems[J]. IEEE Transactions on Power Systems, 1999, 14(1): 355-361.

[16]AKHAVEIN A, FOTUHI-FIRUZABAD M, BILLINTON R, et al. Adequacy equivalent development of composite generation and transmission systems using network screening[J]. IET Generation, Transmission & Distribution, 2011, 5(11): 1141-1148.

[17]汪兴强, 丁明, 韩平平. 互联电力系统可靠性评估的改进等效模型[J]. 电工技术学报, 2011, 26(9): 201-207. WANG Xingqiang, DING Ming, HAN Pingping. An improved equivalent model for reliability evaluation in interconnected power system[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 201-207.

[18]李江,刘伟波, 李国庆, 等. 基于序贯蒙特卡罗法的复杂配电网可靠性分析[J]. 电力建设, 2015, 36(11): 17-23. LI Jiang, LIU Weibo, LI Guoqing, et al. Reliability analysis of complex distribution network based on sequential Monte Carlo method[J]. Electric Power Construction, 2015, 36(11): 17-23.

[19]程林, 王旭, 黄俊辉, 等. 基于配网重构的交直流混联配电网可靠性分析[J]. 电力建设, 2016, 37(5): 2-9. CHENG Lin, WANG Xu, HUANG Junhui, et al. Reliability analysis of AC/DC hybrid distribution network based on network reconfiguration[J]. Electric Power Construction, 2016, 37(5): 2-9.

[20]赵渊, 周家启, 周念成, 等. 发输电系统可靠性评估的启发式就近负荷削减模型[J]. 电网技术, 2005, 29(23): 34-39. ZHAO Yuan，ZHOU Jiaqi，ZHOU Niancheng, et al. A heuristic approach to local load shedding scheme for reliability assessment of composite generation and transmission system[J]. Power System Technology, 2005, 29(23): 34-39.

[21]BILLINTON R,LI W Y. Reliability assessment of electric power systems using Monte Carlo methods[M].New York, USA: Plenum Press,1994: 209-254.

[22]王彤, 卢斯煜, 金小明, 等. 风电并网对南方电网可靠性的影响评估[J]. 电力建设, 2015, 36(10): 161-166. WANG Tong，LU Siyu，JIN Xiaoming, et al. Influence assessment of wind power integration on China southern power grid reliability[J]. Electric Power Construction, 2015, 36(10): 161-166.

[23]LI W, MUKERJI R, PATTON D. A report prepared by the reliability test system task force of the application of probability methods subcommittee[J].IEEE Transactions on Power Systems，1999，14(3)：1010-1020.

(编辑 景贺峰)

Power System Reliability Evaluation Based on Network Partition and Coordination Optimization of Power Support Capability

JIN Liming1，ZHOU Ning1，FENG Li1，LU Zhiran2，ZHAO Yuan2

(1.State Grid Chongqing Electric Power Company, Chongqing 400015, China; 2. State Key Laboratory of Power Transmission Equipment & System Security and New Technology (Chongqing University), Chongqing 400044, China)

To alleviate the calculation complexity of power system reliability evaluation, this paper proposes a reliability evaluation model for power system based on network partition and coordination optimization of power support capability. This model determines the coordination solution sequence of subareas according to the generation margin, takes the tie line power between subareas as equivalent loads at the boundary nodes of subareas, and adopts the optimal load shedding model to optimize the load curtailment and power support capabilities of subareas successively according to the coordination solution sequence. Compared with the conventional partition equivalence technique of power system reliability evaluation, the proposed network partition and coordination model can realize the effective modeling of the power support capabilities among subareas, and enhance the reliability evaluation efficiency of power system while guaranteeing high accuracy, due to considering the generation margin and power flow constraints of subareas and adopting the optimization model to calculate the maximum equivalent load of subareas. Finally, this paper verifies the rapidity and effectiveness of the proposed model through IEEE-RTS96 test system.

power system reliability; equivalent load; generation margin; network partition and coordination

国家自然科学基金项目(50977094)

TM 732

A

1000-7229(2016)10-0069-11

10.3969/j.issn.1000-7229.2016.10.010

2016-05-22

金黎明(1982)，男，硕士，高级工程师，主要研究方向为电力系统运行分析和控制；

周宁(1972)，男，硕士，高级工程师，主要研究方向为电力系统自动化；

冯丽(1975)，女，博士，高级工程师，主要研究方向为电力系统运行分析和控制；

卢治燃(1989)，女，硕士研究生，主要研究方向为电力系统规划与可靠性评估；

赵渊(1974)，男，博士，教授，博士生导师，主要研究方向为电力系统规划与可靠性。

Project supported by National Natural Science Foundation of China(50977094)