一种恢复电压和频率的微网改进下垂控制方法
2017-01-09张鑫洲王维庆王海云
张鑫洲,王维庆,王海云
(新疆大学电气工程学院可再生能源发电与并网技术教育部工程研究中心,乌鲁木齐市 830047)
一种恢复电压和频率的微网改进下垂控制方法
张鑫洲,王维庆,王海云
(新疆大学电气工程学院可再生能源发电与并网技术教育部工程研究中心,乌鲁木齐市 830047)
目前,微网孤岛控制的实现一般都是基于下垂控制。下垂控制不仅可以保证电压和频率的稳定性,而且可以实现各分布式电源的负荷合理均摊。但是对于电能质量需求较高的情况,下垂控制后一般都会进行二次电压和频率的恢复控制,这就造成了运行成本的提高。针对这种问题,对下垂控制原理进行分析,提出了一种基于“冲洗过滤”恢复电压和频率的方法,该方法在下垂控制前引入了一个“冲洗过滤”控制器,实现了不增加二次通信线路进行电压和频率的恢复。利用PSCAD/EMTDC软件平台进行了模拟实验验证,结果表明,该方法能很好地在微网负荷变化后对电压跌落和频率偏差进行恢复。
孤岛微网;下垂控制;冲洗过滤
0 引 言
微网可以运行于并网和孤岛2种状态[1]。微网并网运行时,其电压和频率由接入的大电网进行支撑;微网孤岛运行时,其电压和频率则需要依靠控制器调整来保持自身稳定[2-4]。在一般的孤岛微网控制中,下垂控制占据了主导地位,研究改进下垂控制具有很好的实际意义。
目前大部分的下垂控制研究方向都是如何能更好地实现合理分配负荷和功率,但对于下垂控制后的电压和频率恢复的研究很少。传统的下垂控制策略相当于电网的一次调频环节,属于有差调节,无法使微网在负荷变化后频率和电压恢复到原设定值,这就会给后续控制造成比较大的偏差。为了解决这类问题,二次分层控制策略被提了出来[5-8]。文献[5]采用了平移下垂曲线的二次控制,需用能量管理系统(engerey mangment system,EMS)定时采集输出功率,用新的下垂曲线整定,然后下发到各个控制源。文献[6]将各个逆变器的输出信息,传送到中央控制器,计算信息,然后返回本地控制器。文献[7]用第n个逆变器的控制信息计算补偿给第n+1个逆变器,使其系统整体达到稳定。文献[8]采用2个逆变器为单元,一个采用传统控制,另一个逆变器以第1个为基础进行参数的整定。文献[7]和[8]的原理一样,都需要通过通信线路传输上一个逆变器控制信息。二次控制(集中式[5-6]和分布式[7-8])的控制结构都要求通信线路,使得控制复杂和成本昂贵;此外依赖通信连接的高层次控制,增加了系统出现故障的可能性,降低了系统可靠性和稳定性。考虑到控制的成本和流程简化,新的基于无通信线路的本地控制被提出[9-14]。文献[9-10]将电压和相角偏差作为前馈量加入功率下垂控制环节,实现电压和相角的二次调整,但只是对频率的偏差进行了修正,电压的恢复没有探讨。文献[11]采用了频率限制控制器,将母线的频率与基准频率的差值通过调节器补偿系统有功盈缺。文献[12]在下垂控制中加入电压和频率偏差的前馈调节,从实验结果看只是保证了电压和频率保持了较低的跌落率后继续运行,没有恢复的效果。文献[13]将光蓄单元作为动态调压装置进行电压恢复,该方法只针对于有光伏发电单元的微网,比较特定。文献[14]在传统控制中分别对电压、有功功率、无功功率设计了3种不同的控制器,策略效果很好,但是控制方法实现起来比较麻烦,需要进行3次参数整定设计。上述方法中要么只是有单一的调节(频率[8-11]、降低跌落[12]、电压[13]),要么虽然两者都考虑[14],但设计复杂,可操作性和实际用途不大。
本文在对传统下垂控制原理进行分析后,提出一种能快速恢复电压和频率的“冲洗过滤”控制器,给出冲洗过滤器的设计原理和推导。该控制器策略可以在不影响系统功率分配的基础上使下垂控制后系统的电压和频率恢复到预定水平,免去传统下垂控制后需要进行电压和频率整定的二次控制。最后在微网仿真系统上对所提出的改进策略进行仿真验证,证明策略的合理性与有效性。
1 传统下垂控制
图1为分布式电源并网等效图。如图1所示,对于一个给定的配电线路阻抗,电源系统两电压U∠φ到UL∠0之间有功功率和无功功率满足物理关系:
(1)
(2)
式中:U和UL分别表示分布式逆变器滤波后输出电压和公共连接点(point of common coupling,PCC)电压;φ是U和UL之间相位差;Z∠θ表示线路阻抗。

图1 分布式电源并网等效图
在高压和中压的微电网中,由于高感性元件以及容性滤波,线路阻抗常被考虑为感性(θ=90°)。由于微网中相位差φ通常相当小,所以有sinφ≈φ,cosφ≈1。因此,公式(1)和(2)可被简化为:
(3)
(4)
公式(3)和(4)的关系就是有功功率-频率 (P-ω)和无功功率-电压(Q-U)下垂控制的基础,如图2所示。
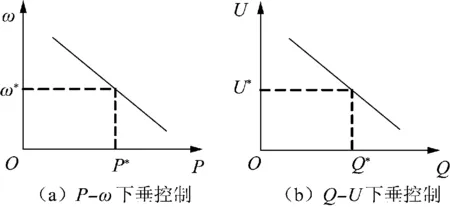
图2 传统下垂控制特性曲线图
(5)
Ui=U*-nq(Qi-Q*)
(6)
式中:ωi和Ui分别为第i个逆变器的角频率和电压幅值给定值;Pi和Qi是经测量得出的有功功率和无功功率;P*和Q*分别为有功功率和无功功率的参考值;mp和nq分别为P-ω和Q-U的下垂控制系数。
2 改进控制设计
2.1 冲洗过滤器设计
定义ΔPi=Pi-P*,Δωi=ωi-ω*,ΔUi=Ui-U*,ΔQi=Qi-Q*,代入公式(5)和(6),并两边对时间求导,得到:
(7)
(8)
式(7)和式(8)可以确保在稳定状态下的功率共享,但是不能恢复电压和频率。通过增加1个Δωi恢复因子和1个ΔUi恢复因子,得到:
(9)
(10)
式中:kp和kq为滤波器常数。由于系统在稳定运行时,公式(9)和(10)里的导数项为0,所以方程在再次稳定运行时会强制使得Δωi和ΔUi值为0,使系统再次稳定后,频率和电压恢复到原值。对式(9)和式(10)进行拉普拉斯变换,得到:
sΔωi(s)+mpsΔPi(s)+kpΔωi(s)=0
(11)
sΔUi(s)+nqsΔQi(s)+kqΔUi(s)=0
(12)
传递函数的形式为:
(13)
(14)
再将定义的Δωi、ΔUi、ΔPi、ΔQi代入,公式(13)和(14)可改写为:
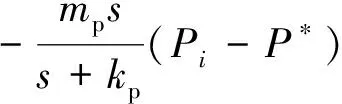
(15)
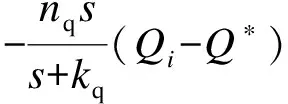
(16)
公式(15)和(16)可以被看作是一个基于“冲洗过滤”的动态控制。控制器的框架如图3所示。“冲洗过滤”的数学实质就是一个一阶的高通滤波器,拒绝信号的直流分量和通过信号的暂态分量。

图3 冲洗过滤器的框架图
冲洗过滤器是一个高通滤波器,冲刷(拒绝)稳态输入,同时通过瞬态输入,在连续时间设定中,1个典型的高通滤波器传递函数为[15]
(17)
式中d是过滤器时间常数的倒数,当为稳定滤波器时,d为正,当为不稳定滤波器时,d为负。
(18)
在连续时间里,过滤器可表示为

(19)
输出方程为
y=x-dz
(20)
在离散时间里,过滤器可表示为
z(k+1)=x(k)+(1-d)z(k)
(21)
输出方程为
y(k)=x(k)-dz(k)
(22)
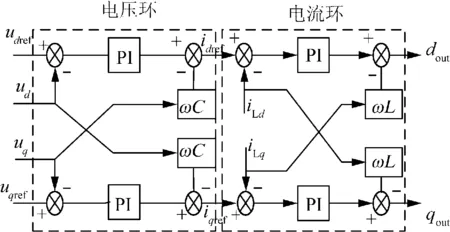
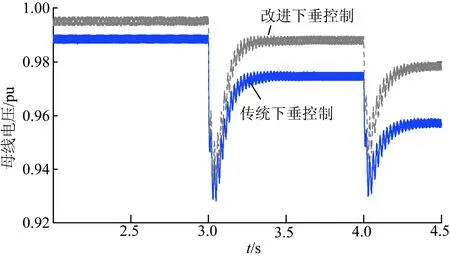
对于一个稳定的过滤器,滤波器常数d满足0 冲洗过滤的主要优点在于使系统目标操作点的鲁棒参数不确定[15],因此,本文所提控制方法可以在系统负载变化后保持基准电压和频率,而单纯的静态反馈和各种前馈补偿控制以及通过改变系统参数控制可能改变系统目标操作点,造成负荷变化后,系统回到稳定运行时,偏离了原来设定的目标点。 2.2 系统其余控制设计 逆变器系统整体控制如图4所示。根据瞬时功率理论,逆变器输出的实时有功功率和无功功率表达式为 图4 控制整体框架图 (23) 经过低通滤波器后, (24) 式中:ud、uq、id、iq分别表示图4中uabc和iabc的d轴和q轴分量;ωc为低通滤波器截止频率。 同步旋转坐标系下的电压环和电流环的控制策略如图5所示。图5中:iLd和iLq为滤波电感电流的d轴和q轴的分量。L和C分别为LC滤波器的电感值和电容值。 图5 电压电流控制环 由于本文所讨论重点是电压和频率的恢复问题,为了减少不必要的参数影响,故对实验仿真模型进行了理想化处理,2条线路参数都为纯电感,完全符合理想下垂控制条件,理想的直流电源代替分布式电源,负载为对称的三相负载。基于PSCAD/EMTDC平台搭建了2台容量为1.5 MW逆变器组成的孤岛微网仿真系统,仿真结构图如图6所示。系统运行参数如表1所示。 图6 仿真拓扑图 仿真运行的条件为:0 s时2台逆变器同时带负荷(S=450 kW+250 kV·A)启动;稳定运行3 s后系统投入(S=350 kW+250 kV·A)混合负荷;4 s后系统投入(Q=350 kV·A)纯无功负荷。图7—9为仿真实验结果。 图7为母线上频率的变化曲线。从图7中可以看出:系统稳定运行时,传统下垂控制时,公共母线频率保持为50.28 Hz,加入“冲洗过滤”后的微网稳定运行频率为50.01 Hz;3 s后负荷投入,此时传统下垂控制跌落了0.27 Hz之后回到了50.12 Hz,频率跌落了0.16 Hz,并没有返回到原设定值,而加入“冲洗过滤”后的控制策略,频率跌落0.21 Hz后在0.5 s时就恢复到了原有的50.01 Hz;4 s时系统无功负荷投入后,加入“冲洗过滤”后的控制策略比传统控制策略下,频率更快回到原有值。 图7 微网频率波形 图8为母线上电压的变化曲线。如图8所示,微网稳定运行时,传统下垂控制下,电压维持在 0.990 pu,而本文所提加入“冲洗过滤”控制策略,电压保持在0.996 pu,几乎接近真实值;3 s后投入有功和无功负荷后,传统控制策略下,电压在恢复后仍跌落0.016 pu,加入“冲洗过滤”的控制策略的母线电压恢复后跌落为0.006 pu,电压跌落率降低了10%,并 图8 母线电压的比较 且恢复速度也快于传统下垂控制;4 s后无功负荷的投入使母线电压得到了恢复,加入“冲洗过滤”控制也明显好于传统下垂控制。 图9为逆变器输出功率曲线。由图9可得:在负荷功率分配上,传统控制和本文所提加入“冲洗过滤”2种策略无明显大的变化。本文所提方法由于在3 s负荷变化时对系统频率和电压进行了恢复控制,使得4 s负荷变化后的有功输出和无功输出与实际功率更接近。可以得出基于本文所提改进的下垂控制策略不会影响原系统的功率分配。 图9 单个逆变器输出功率 (1)设计原理清楚,推导简单。不需要特别的优化设计,并且系统在加入“冲洗过滤”后不影响原有的功率分配,不会造成系统整体性能的变化。 (2)加入冲洗过滤后的下垂控制对频率和电压有很好的稳定和恢复能力,对于微网电能质量有很好的支撑能力,去除了一般下垂控制后需要恢复电压和频率的二次控制,节约了运行成本。 (3)不针对任何一种特定的分布式电源,具有很好的适用性。 [1]刘强, 周林, 郭珂. 微电网的动态特性及控制策略分析[J]. 电力建设, 2014, 35(6):31-37. LIU Qiang, ZHOU Lin, GUO Ke. Analysis on the dynamic characteristics and control method of microgrid[J]. Electric Power Construction, 2014, 35(6):31-37. [2]王杨,万凌云,胡博,等. 基于孤岛运行特性的微电网可靠性分析[J]. 电网技术, 2014, 38(9): 2379-2385. WANG Yang, WAN Lingyun, HU Bo, et al. Isolated island operating characteristics based analysis on reliability of microgrid[J]. Power System Technology, 2014, 38(9): 2379-2385. [3]宋洪磊, 李晓飞, 吴俊勇,等. 解列后电力孤岛的校正控制策略研究[J]. 电力建设, 2016, 37(4):124-130. SONG Honglei, LI Xiaofei, WU Junyong, et al. Correction control strategy of islanded power grid after separation[J]. Electric Power Construction, 2016, 37(4): 124-130. [4]王波, 张保会, 郝治国. 基于功率监测和频率变化率的孤岛微电网紧急切负荷控制[J]. 电力系统自动化, 2015, 39(8): 33-37. WANG Bo, ZHANG Baohui, HAO Zhiguo. Emergency load shedding control for islanded microgrid based on power monitoring and rate of frequency change[J]. Automation of Electric Power Systems, 2015, 39(8): 33-37. [5]鲍薇, 胡学浩, 李光辉,等. 基于同步电压源的微电网分层控制策略设计[J]. 电力系统自动化, 2013, 37(23): 20-26. BAO Wei, HU Xuehao, LI Guanghui, et al. Synchronous voltage source based design of hierarchical control strategy for microgrid[J]. Automation of Electric Power Systems, 2013, 37(23): 20-26. [6]孙孝峰, 杨雅麟, 赵巍, 等. 微电网逆变器自适应下垂控制策略[J]. 电网技术, 2014, 38(9): 2386-2391. SUN Xiaofeng, YANG Yalin, ZHAO Wei, et al. An adaptive droop control method for inverters in microgrid[J]. Power System Technology, 2014, 38(9): 2386-2391. [7]LIANG J, JI Y, WU W, et al. AC/DC hybrid micro grid voltage recovery control[C]//2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT). Changsha: IEEE, 2015: 1256-1260. [8]孙孝峰, 王娟, 田艳军, 等. 基于自调节下垂系数的DG逆变器控制[J]. 中国电机工程学报, 2013, 33(36): 71-78. SUN Xiaofeng, WANG Juan, TIAN Yanjun, et al. Control of DG connected inverters based on self-adaptable adjustment of droop coefficient[J]. Proceedings of the CSEE, 2013, 33(36): 71-78. [9]张明锐, 杜志超, 黎娜, 等. 高压微网孤岛运行时频率稳定控制策略研究[J]. 中国电机工程学报, 2012, 32(25): 20-26. ZHANG Mingrui, DU Zhichao, LI Na, et al. Control strategies of frequency stability for islanding high-voltage microgrids[J]. Proceedings of the CSEE, 2012, 32(25): 20-26. [10]李坦, 杨洪耕, 齐少鹏, 等. 基于P/δ下垂控制的低压微电网频率控制策略[J]. 电测与仪表, 2015, 52(7): 66-70. LI Tan,YANG Honggeng,QI Shaopeng, et al. Control strategy for low-voltage microgrid frequency based onP/δdroop control[J]. Electrical Measurement & Instrumentation, 2015, 52(7): 66-70. [11]吕思卓, 郑超, 杨金刚,等. 送端直流孤岛系统频率限制器优化控制策略[J]. 电力建设, 2016, 37(2): 107-111. LYU Sizhuo, ZHENG Chao, YANG Jingang, et al. FLC optimization control strategy of islanded HVDC sending system[J]. Electric Power Construction, 2016, 37(2): 107-111. [12]孙孝峰, 吕庆秋. 低压微电网逆变器频率电压协调控制[J]. 电工技术学报, 2012, 27(8): 77-84. SUN Xiaofeng, LYU Qingqiu. Improved PV control of grid-connected inverter in low voltage micro-grid[J]. Transactions of China Electrotechnical Society, 2012, 27(8): 77-84. [13]成瑞芬, 韩肖清, 王鹏,等. 微电网动态电压恢复器运行模式研究[J]. 电网技术,2013, 37(3):610-615. CHENG Ruifen, HAN Xiaoqing, WANG Peng, et al. Research on operation modes of dynamic voltage restorer in microgrid[J]. Power System Technology, 2013, 37(3):610-615. [14]NASIRIAN V, SHAFIEE Q, GUERRERO J M, et al. Droop-free team-oriented control for AC distribution systems[C]//2015 IEEE Applied Power Electronics Conference and Exposition (APEC). Charlotte, NC: IEEE, 2015: 2911-2918. [15]HASSOUNEH M A, LEE H C, ABED E H. Washout filters in feedback control: benefits, limitations and extensions[C]// American Control Conference, 2004. Proceedings of the 2004. Boston, MA, USA: IEEE, 2004: 3950-3955. (编辑 景贺峰) An Improved Droop Control Method for Voltage and Frequency Restoration in Microgrid ZHANG Xinzhou, WANG Weiqing, WANG Haiyun (Engineering Reasearh Center of Education Ministry for Renewable Energy Power Generation and Grid Technology, College of Electrical Engineering, Xinjiang University, Urumqi 830047, China) At present, the realization of the island microgrid control is generally based on droop control. The droop control can not only ensure the stabilities of voltage and frequency, and realize the reasonable load sharing of distributed generation. But for the high demand of power quality, there will normally be the recovery control of the voltage and frequency for the second time after droop control, which results in the increase of operating costs. In view of this problem, this paper proposes a method based on the ‘washing and filtering’ to restore the voltage and frequency after the analysis of the droop control principle. This method introduces a ‘washing and filtering’ controller before droop control, which can restore the voltage and frequency without increasing the secondary communication line. Through the simulation experiment in PSCAD/EMTDC software platform, the results show that this method can recover the voltage drop and the frequency deviation after the load change of microgrid. island microgrid; droop control; washing and filtering 新疆维吾尔自治区重点实验室项目(2016D03021);国家高技术研究发展计划项目(863计划)(2013AA05064);教育部创新团队项目(IRT1285);新疆维吾尔自治区重大攻关项目(201230115-3);新疆科技厅课题项目(2015KL020) TM 711 A 1000-7229(2016)10-0048-06 10.3969/j.issn.1000-7229.2016.10.007 2016-05-20 张鑫洲(1988),男,硕士研究生,主要研究方向为新能源并网技术; 王维庆(1959),男,教授,博士研究生导师,主要研究方向为电力系统自动化和风电机组智能控制; 王海云(1973),女,博士,副教授,硕士研究生导师,主要研究方向为可再生能源发电与并网技术。 Project supported by the National High Technology Research and Development of China(863 Program)(2013AA05064)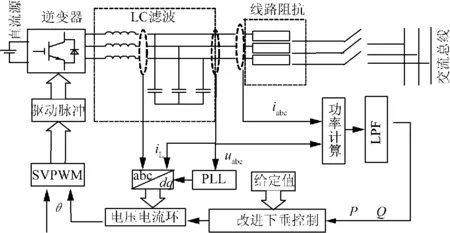
3 仿真实验验证




4 结 论
