最小信息熵的优化算法在轨道电路故障诊断中的运用

吴志鹏

(西南交通大学信息科学与技术学院，成都 611756)

最小信息熵的优化算法在轨道电路故障诊断中的运用

吴志鹏

(西南交通大学信息科学与技术学院，成都 611756)

在使用决策树算法解决ZPW-2000A无绝缘轨道电路故障诊断问题中，由于轨道电路的数据中大部分属性值都是连续的，所以在采用决策树方法时必须对这些属性值离散化。主要对最小信息熵算法处理连续属性值离散化过程进行分析，并且对其离散化过程进行一定的优化来提高计算效率，缩短计算时间。

轨道电路；决策树；最小信息熵算法；离散化

ZPW-2000A无绝缘轨道电路目前在我国铁路运营线路中使用十分普遍。轨道电路一般都布置在铁路沿线的车站和区间，其设备主要分为室内和室外两部分且结构较复杂，加上其使用环境的复杂性等因素给轨道电路的维护带来困难。目前轨道电路的日常维护工作主要以人工为主[1]。

决策树算法是一种典型的分类方法，首先对样本数据进行处理，利用归纳算法生成决策树和规则，再使用生成规则对新数据样本进行分类。决策树算法具有分类快、精度高、分类规则容易理解等特点；另外，决策树C4.5算法[2]能够处理连续值属性，且准确率较高，因此可以运用到ZPW-2000A轨道电路故障诊断中。关于铁路信号设备故障诊断已经有学者使用决策树C4.5算法对其进行研究[3-4]。

1 最小信息熵算法

在使用决策树算法处理数据之前，先观察数据，如果存在连续值，需要将连续值离散化。假设故障样本集合为S={S1，S2，…，Sn}，共计n个，条件属性p个，以及i种故障类型。本文仅针对连续值属性p1使用最小信息熵算法[5]进行分析。

步骤1：根据式（1）确定离散分类数m,一般m取2或3，即离散分类数为2类或3类。本文以m=3分析。

步骤2：将所有样本按条件属性p1的取值升序排列，排序后取属性p1值的集合为S'，S'={S1'，S2'，…，S'n}，其中S'i≤S'i+1，1≤i≤n-1。在集合S'中，分别计算两两相邻属性值的平均值x，即x=（S'i+S'i+1)/2，其中1≤i≤n-1，这样x把集合S'划分为两个子区间[S'1，x]和[x，S'n],分别记这两个区间为P区间和Q区间。然后计算x的信息熵E （x），比较各个x计算出的信息熵E（x），找出得到最小信息熵E（x）时的x，记作x'，此时的x'就是最佳分割阈值，根据式（2）～（8）计算信息熵E（x）：

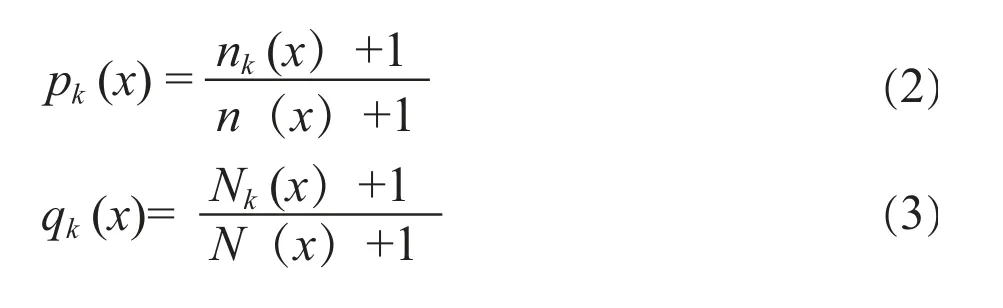
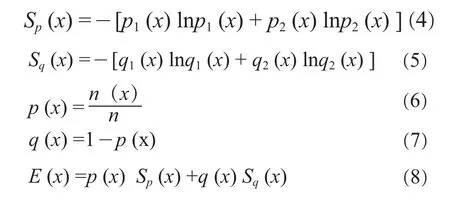
其中：

nk（x)和Nk（x)分别表示在P区间和Q区间内故障类型为k的样本数；n（x)和N（x)分别表示在P区间和Q区间内的样本总数；n表示所有样本总数；pk（x)和qk（x)分别表示在P区间和Q区间内故障类型为k的条件概率；p（x)和q（x)分别表示在P区间和Q区间内样本的概率。

步骤5：对所有条件属性值根据步骤1～4进行离散化后，再根据决策树C4.5算法进行分类。

2 对最小信息熵算法的改进

对最小信息熵算法步骤2的改进，分为以下2种情况。

1）集合S'中属性p1不存在连续值相等的情况

根据Fayyad[6]等学者已经证明的结论：不管样本集合类别（本文中类别指故障类型）有多少，连续值属性的最佳分割点总在边界点处，总在边界点处。按照Fayyad等的结论可以做如下处理：因为连续值属性最佳分割点在边界点处，为了得到边界点，所以将n个样本按属性p1的取值升序排列，排序后取属性p1值的集合为S'，S'={S1'，S2'，…，S'n}，其中Si' ≤Si'+1，1≤i≤n-1。把排序后的样本按故障类型分为m组(m≤n)：F1，…Fm，每组中的故障类型都是同一种，但相邻两组的故障类型不相同，相邻两组边界处的样本为边界点，且这相邻两组中每组都有一个边界点，这两个边界点对应样本属性p1值的平均值x作为一个备选分割阈值，共有m-1个备选分割阈值，x同样把集合S'划分为两个子区间[S'1，x]和[x，Sn' ]，分别记这两个区间为P区间和Q区间。然后计算x的信息熵E（x），比较各个x计算出的信息熵E（x），找出得到最小信息熵E（x）时的x，记作x'，此时的x'就是最佳分割阈值。

比如在表1中，样本数量为7，故障类型数量为2，分别为f1和f2。照上面的方法把7个样本按属性p1的取值升序排列后，将样本分为4组，F1包含样本1，F2包含样本2和3，F3包含样本4和5，F4包含样本6和7，所以只需要计算3个备选分割阈值，分别是15，17.5和19.5，而如果用原来的方法要计算6个备选分割阈值。

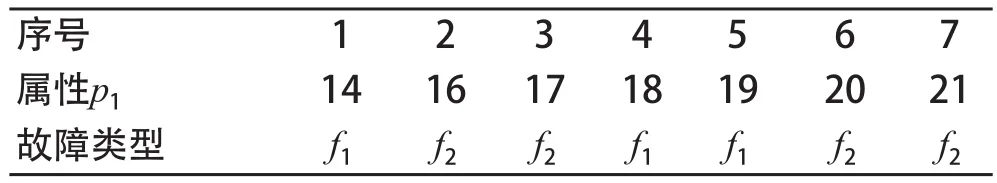
表1 集合S'中不存在连续值相等的升序排列

2）集合S'中属性p1存在连续值相等的情况

如果集合S'中属性p1存在连续值相等的情况，则按属性p1的取值升序排列，可能出现2种结果，如表2和3所示。如果直接使用1）中的方法，表2中属性p1的备选分割阈值是16.5和17，表3中属性p1的备选分割阈值是17和17.5，所以排序不一样可能导致最后得到的最佳分割阈值不同。这时在考虑使用1）中方法计算备选分割阈值外，还要把属性p1中出现的相等值、相等值的相邻值与相等值的平均值x作为备选分割阈值。x同样把集合S'划分为两个子区间，分别记这两个区间为P区间和Q区间。然后计算x的信息熵E（x），比较各个x计算出的信息熵E（x），找出得到最小信息熵E（x）时的x，记作x'，此时的x'就是最佳分割阈值。在表2中，需要计算3个备选分割阈值，分别是16.5，17和17.5，而用原来的方法要计算6个备选分割点。

对最小信息熵算法步骤3的改进：

表2 集合S'第一种升序排列

表3 集合S'第二种升序排列

得到的最佳分割阈值x'，将集合S'={S1'，S2'，…，Sn' }分为2个子集S'1和S'2，S'1={S'i│S'i≤x', 1≤i≤n}，S'2={Si' │S'i＞x',1≤i≤n},将子集S1'和S2'根据改进后的步骤2分别计算出最佳分割阈值x1'和x'2，此时一共得到3个分割阈值，它们的关系是x1' ＜x' ＜x2' 。

3 比较分析

试验采用某站ZPW-2000A轨道电路历史数据样本，每个样本包含的连续属性有功出电压、送端电缆模拟网络电缆侧电压、主轨道输入电压、“轨出1”电压、小轨道输入电压、“轨出2”电压等6种，另外还包含非连续属性如XGJ电压状态，如表4所示。数据样本包含发送端网络盘故障、共用发送通道故障、衰耗盘故障、主轨故障、小轨故障、发送器端子到零层端子间故障等6种常见故障。

表4 属性及符号表示

1）耗时比较

分别对数据样本中的连续属性使用改进前和改进后的最小信息熵算法进行离散化处理，因为离散化中信息熵E（x)的计算占了绝大部分时间，故试验考虑计算信息熵E（x)的次数来反映优化效果，如表5所示。

2）离散化结果比较

离散化的结果取决于样本值和最佳分割阈值，根据最佳分割阈值将样本连续属性划分为离散值，使用改进前和改进后的最小信息熵算法分别对样本进行离散化处理，两种方法得到的离散化结果一致，说明改进后的最小信息熵算法的离散化正确率较高。部分样本离散化后结果如表6所示。

表5 计算信息熵次数试验结果

表6 离散化后部分数据样本

3）故障诊断试验

将214组训练样本使用优化后的最小信息熵算法将轨道电路样本数据进行离散化，然后用决策树算法进行规则提取，再将规则运用到故障诊断中用于故障匹配。采用40组测试样本进行测试，将诊断结果和实际结果相对比。如果两者一致，表示诊断正确，如果两者不一致，表示诊断错误。结果表明，诊断正确率为80%，具有一定的有效性。其中部分诊断结果为“无”，表明故障不在样本包含故障类型中或是无法判断是其中的哪种故障，部分试验结果如表7所示。

表7 诊断试验部分结果

综上所述，使用优化后方法在求最佳分割阈值过程中，信息熵E（x)的计算量有明显的减少。样本数量越大，连续属性中出现相同值概率越大，优化效果将更加明显，节省的运算时间将更多。此外使用优化后方法进行离散化得到正确率也较高，保证了离散化的准确性，故障诊断中实际结果与诊断结果也基本一致，说明采用优化后的最小信息熵算法一定程度上适用于ZPW-2000A无绝缘轨道电路的故障诊断。

4 结论

通过对最小信息熵算法进行优化，运用优化的最小信息熵算法对连续属性进行离散化处理，不仅提高运算效率，而且将离散化后样本数据用于基于决策树算法的轨道电路故障诊断中也具有一定的有效性。但ZPW-2000A轨道电路数据量大，在对其使用优化的最小信息熵算法进行离散化处理过程中，由于不同线路区段的轨道电路特征参数工作值都不完全相同，所以在兼容性方面还需要进一步的研究和改进。

[1]孙上鹏.无绝缘轨道电路故障诊断方法研究[D]. 北京：北京交通大学，2014.

[2]黄文.决策树的经典算法∶ID3与C4.5[J].四川文理学院学报，2007（5）：16-18.

[3]刘扬.基于决策树的轨道电路故障诊断知识表示方法研究[J].邵阳学院学报(自然科学版)，2014（4）：18-23.

[4]王继强.C4.5算法在信号设备故障诊断中的应用研究[J].电子世界，2012（9）：107-109.

[5] Chen J S，Cheng C H.Extracting classification rule of software diagnosis using modified MEPA[J].Expert Systems with Applications, 2008，34（1）：411-418.

[6] Fayyad U M，Irani K B.On the handling of continuous-value attributes in decision tree generation[J].Machine Learning，1992，8（1）：87-102.

When the decision tree algorithm is used to solve fault diagnosis problems of ZPW-2000A jointless track circuits, the attribute values must be discretized because most of the attribute values in track circuit data are continuous. This paper mainly analyzes the process of continuous attribute values discretization based on the minimum entropy principle approach, and introduces the methods to improve the computing effi ciency and reduce the computation time by optimizing the discretization process.

track circuit; decision tree; minimum entropy principle approach; discretization

10.3969/j.issn.1673-4440.2016.06.024

2015-12-30）