基于加权相对灵敏度的驾驶室结构轻量化

陈 剑 杜选福 施斐博

合肥工业大学，合肥，230009

基于加权相对灵敏度的驾驶室结构轻量化

陈 剑 杜选福 施斐博

合肥工业大学，合肥，230009

建立了某卡车驾驶室结构有限元模型，通过实验与数值模态分析的对比验证了模型的准确性。对驾驶室构件直接进行灵敏度分析，通过层次分析法确定约束响应的权重系数，并考虑约束响应可变裕度。在此基础上提出加权相对灵敏度概念并据此确定设计变量及其优化方向。在保证驾驶室主要静动态性能不降低的前提下，优化驾驶室部分构件厚度。优化后的驾驶室质量比优化前减小了8.7%，主要静动态性能均有不同程度的提高,车内低频噪声略有升高。

加权相对灵敏度；模态分析；刚度；轻量化

0 引言

节能与环保是现代汽车设计研究的重点目标之一。研究表明，汽车总质量每减轻10%，燃油消耗量可以降低6%～8%[1]，汽车轻量化设计已成为汽车设计制造的主流方向。

汽车轻量化设计主要通过结构优化、新材料替代以及应用先进制造工艺等方法实现，其中结构优化往往能够以较小的物料成本和对项目投资的影响获得较大的减重收益[2]。基于灵敏度的汽车结构轻量优化方法通过灵敏度分析选择优化变量，约束弯扭刚度和主要低阶模态，以质量或体积最小为目标[3]，或是在此基础上综合考虑碰撞安全性优化减重[4-5]。目前有关驾驶室轻量化设计的研究正朝着多工况、多目标和多学科集成的方向深入[6-8]。

本文以某商用车驾驶室为研究对象，建立驾驶室有限元分析模型，通过实验与数值模态分析结果对比验证了有限元模型的准确性。对驾驶室构件进行灵敏度分析，应用层次分析法确定弯曲刚度、扭转刚度、一阶弯曲模态的频率(一阶弯频)和一阶扭曲模态的频率(一阶扭频)的约束响应权重系数，同时考虑约束响应的可变裕度，在此基础上提出加权相对灵敏度概念，并将其应用到驾驶室构件的变量优选过程中，在保证驾驶室主要静动态性能不改变的前提下进行迭代优化计算。最后利用耦合声学有限元法计算分析轻量化前后驾驶室内部声学特性变化情况。

1 有限元模型的建立

1.1 驾驶室有限元模型

本文所分析的驾驶室是由复杂的空间板壳结构经过点焊连接而成的。驾驶室板件由四节点或三节点壳单元来模拟，点焊由ACM2来模拟，螺栓等连接由RBE2来模拟。在建模的过程中要对模型进行简化以提高网格质量和计算速度。在HyperMesh软件中建立驾驶室结构有限元模型，整个模型的网格单元平均尺寸为10 mm，节点数为332 724个，四边形单元为309 993个，三角形单元为13 322个，三角形单元所占比例约为4%。采用Block Lanczos方法提取驾驶室有限元模型模态参数如表1所示。其中一阶扭转模态频率为45.23 Hz，振型如图1所示。

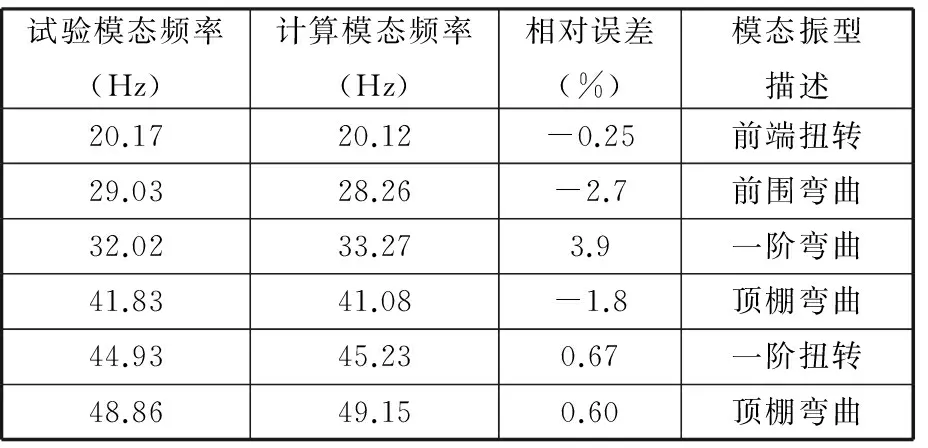
表1 驾驶室计算模态与试验模态结果

图1 驾驶室一阶扭转计算模态振型

1.2 试验模态分析

为了验证驾驶室有限元分析的准确性与可靠性，在试验平台上对驾驶室结构进行模态试验。

采用单点激励多点响应的试验方案，激励信号由力锤发出，响应信号由B&K公司的加速度传感器拾取，测点的连线尽可能地显示驾驶室骨架形状，并避开各阶振型的节点，采用比利时LMS.TSET.LB采集系统进行数据采集和分析，得到驾驶室前6阶试验模态参数如表1所示。

驾驶室模型前6阶主模态频率计算值与试验值误差在4%以内，并且主振型的计算结果和试验结果较一致，表明驾驶室有限元模型精度较高，能准确反映实际的驾驶室特性。

2 驾驶室优化前分析

2.1 刚度分析

在对驾驶室进行刚度分析时，在已经建立的驾驶室有限元模型的基础上，对驾驶室模型进行相应的约束和施加适当的载荷，建立驾驶室弯曲刚度和扭转刚度分析模型。

进行弯曲工况分析时，施加的约束边界条件为约束驾驶室后悬置支座X、Y、Z三个方向的平动自由度以及前悬置Y、Z两个方向的平动自由度。在座椅中心处和驾驶室座椅的四个安装位置之间构建RBE刚性单元，并在RBE上施加垂直向下784 N的力。弯曲工况下的有限元模型如图2所示。分析得到纵梁最大位移为-0.133 mm,相应的弯曲刚度为5824 N/mm。

图2 弯曲工况约束和加载情况

进行扭转工况分析时，其约束条件的施加位置与弯曲刚度分析略有不同，在后悬架支座位置处约束X、Y、Z三个方向的平动自由度以及前段底部横梁中间处Z向的平动自由度，在前悬架支座位置处加载大小相等(3000 N)、方向相反的Z向力。扭转工况下的有限元模型如图3所示。分析得到左右前悬置的位移分别为-1.793 mm、1.744 mm,相应的扭转刚度为9006.5 N·m/(°)。

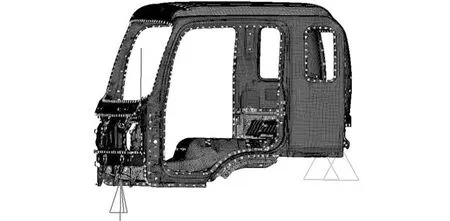
图3 扭转工况约束和加载情况

2.2 模态分析

由于驾驶室在外界激励下的振动是其各阶模态振型叠加的结果，而对振动的主要贡献来自前几阶整体模态，所以在优化过程中约束表1中一阶弯曲模态和一阶扭转模态，可为驾驶室振动性能提供重要依据。

3 加权相对灵敏度分析

3.1 灵敏度分析基本理论

多自由度线性振动动力学方程为

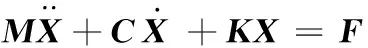
(1)

式中,M、C、K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵；X为系统的位移向量；F为激励向量。

其特征方程为

(2)

j=1,2,…,n

式中，ωj和φj分别为系统第j阶模态频率和模态向量；n为系统自由度。

假设灵敏度分析时有m个设计变量，将式(2)对第i个设计变量xi求偏导得

(3)

(4)

刚度矩阵K对设计变量xi的偏导数可由有限差分方法得到，刚度灵敏度G为刚度K的导数:

(5)

3.2 确定各约束工况的权重

用折中规划法处理多目标问题时，各约束响应的权重系数由设计者依据其重要程度给出经验值，但这种方法主观性强且响应数量越多越难决策[9]。本文选用层次分析法(AHP)确定各约束响应的权重系数。AHP方法通过定性和定量相结合的方式将决策者的经验予以量化，并对决策对象进行优劣排序。

首先建立所评估的问题递阶层次，如图4所示。因为此处只需要确定权重系数，所以只需建立目标层和准则层而不需方案层。然后两两比较约束响应的重要程度，构造判断矩阵A=(aij)m×m,其中aij表示i约束响应对j约束响应的重要程度，m代表需要考虑的工况数量。Satty等[10]提出用数字1～9作为衡量相对重要程度的标度，具体见表2。

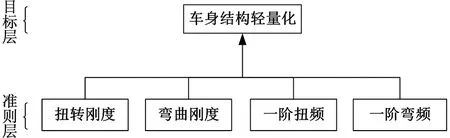
图4 驾驶室结构轻量化递阶层次图

表2 判断矩阵相对重要程度的量化标度参考表

驾驶室必须有足够的刚度以保证其装配和使用要求，同时应用合理的动态特性控制振动和噪声[11]。其中扭转刚度是驾驶室性能的重要指标，必须达到装上挡风玻璃后车身刚度的2/3，也是驾驶室轻量化系数的主要参数[12]。据此确定判定各约束响应重要程度的原则为静态性能大于动态性能，扭转刚度大于弯曲刚度。参考表1构造判断矩阵如下：

扭转刚度 弯曲刚度 一阶扭频 一阶弯频

弯曲刚度

一阶扭频

一阶弯频

当所涉及的因素较多时，判断矩阵中可能会出现甲比乙重要，乙比丙重要，而丙又比甲重要这种逻辑上的错误与混乱，错误的判断矩阵可能会导致决策的失误。为避免这种情况出现，首先需要对判断矩阵一致性进行检测。根据 Satty 等[10]提出的一致性判断准则，判断矩阵可以用一致性比值R来判断矩阵一致性的程度。若

(6)

则表明矩阵的一致性可以接受。其中，IC为一致性指标；m为判断矩阵阶数；λmax为判断矩阵最大特征根；IR为随机一致性指标，由表3查得。

表3 随机一致性指标IR参考值

矩阵A的一致性比值R=0.0171<0.1,因此该矩阵的一致性可以接受,计算判断矩阵A最大特征值λmax对应的特征矢量并将其归一化处理后得到此扭转刚度、弯曲刚度、一阶弯频和一阶扭频约束的权重系数分别为0.5519、0.2421、0.1340、0.0720。

3.3 加权相对灵敏度计算

根据尽量减少优化变量的原则，选取驾驶室81块质量大于0.3 kg板件进行直接灵敏度分析[13]。定义板厚对质量、扭转刚度、弯曲刚度、一阶扭频和一阶弯频的直接灵敏度分别为Sm、Str、Sbr、Stf和Sbf。

(7)

式中，ωtr、ωbr、ωtf和ωbf分别为扭转约束响应、弯曲约束响应、一阶扭频约束响应和一阶弯频约束响应对应的权重系数；RT0、RB0、FT0和FB0分别为扭转刚度、弯曲刚度、一阶扭频和一阶弯频的初值；M0为驾驶室总质量初值；ca为约束裕度系数，此处取相同的值4%。

计算得到驾驶室构件的加权相对灵敏度数值如表4所示。

表4 驾驶室部分构件直接灵敏度和加权相对灵敏度数值

由加权灵敏度的定义可知，ω绝对值较小，表明板件厚度的变化对性能的影响小，通过减小这类板件的厚度实现减重。反之，可以加厚ω值大的板件以提升驾驶室的某些性能。由表4可知，本文研究的驾驶室骨架构件(如纵梁和立柱等)的加权相对灵敏度值较大，驾驶室覆盖件(如前后围板和地板等)的加权相对灵敏度值较小。

4 驾驶室结构轻量化

4.1 驾驶室轻量化的数学模型

基于驾驶室结构刚度和模态的优化问题数学模型为

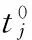
4.2 驾驶室轻量化计算

(1)优化目标。驾驶室质量最小。

(2)约束条件。在弯曲工况下，约束座椅加载点处Z向最大位移量；在扭转工况下，约束前悬架支座位置处Z向最大位移量；模态工况下约束一阶扭转模态和一阶弯曲模态的频率值，设定上述约束量的变化裕度为4%。

(3)设计变量。根据3.2节的分析结果，选定48个加权相对灵敏度较小的板件作为减重件，其厚度变化范围设定为初始厚度的60%～110%，选定20个加权相对灵敏度大的板件作为增厚件，厚度变化范围设定为初始厚度的95%～125%，同时由于顶棚的低阶局部模态较多，将顶棚及其加强横梁也作为增厚件以提高刚度，其余构件不作为变量。同时考虑到材料和改型设计制造成本限制以及后期安全性、NVH性能设计等要求，设定板件厚度下限为0.6 mm，上限为2.0 mm。特别地，构件N_54、N_55(后悬支架)和N_75、N_63(纵梁中焊件)对应ω值很大，初始厚度设为2.0 mm，设定上限为2.5 mm。

(4)优化结果。定义优化收敛容差为5%，即连续两次迭代的目标值相差小于5%，优化求解收敛。经过5次迭代计算，优化过程自动结束，目标函数收敛过程如图5所示。

优化计算得到的构件厚度并不能直接用于实际生产中，根据企业已有的板材规格对优化后的构件厚度进行微调。对微调后模型的刚度和模态进行重新计算，其结果对比如表5所示。

图5 驾驶室质量迭代收敛过程

由表5可知，弯曲刚度和扭转刚度值分别提高了3.7%和4.6%，驾驶室一阶弯曲和一阶扭转频率值分别提高了3%和2.2%，驾驶室质量减小了8.7%。

4.3 车内噪声对比分析

车内结构噪声是由于驾驶室板件结构振动辐射噪声形成的, 这类噪声具有低频特性,是车内噪声最主要的表现形式[14],因此轻量化设计也需要关注车内噪声水平的变化。

首先实验测量驾驶员左右耳与各悬置点之间VTF的振-声传递函数，其中测量左后悬置处激励时主驾右耳VTF的实验装置如图6所示，实验结果如图7所示。其次在驾驶室结构模型的基础上建立了包含座椅的声腔有限元模型，在左后悬置点处施加竖直方向单位激励力，利用声固耦合有限元法计算得到驾驶员右耳位置处声压响应如图7所示。由图7可知，左后悬置-主驾右耳VTF实验和计算声压响应在低频段上整体趋势一致，误差在可接受范围之内，验证了声固耦合模型的准确性。

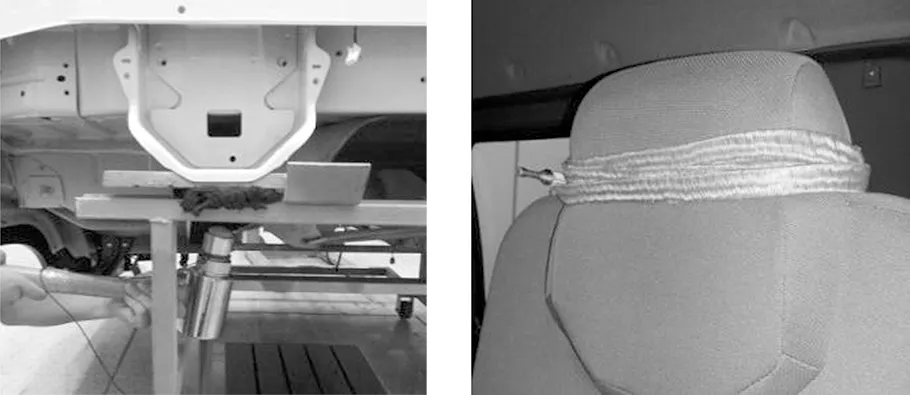
图6 驾驶室VTF实车测试装置

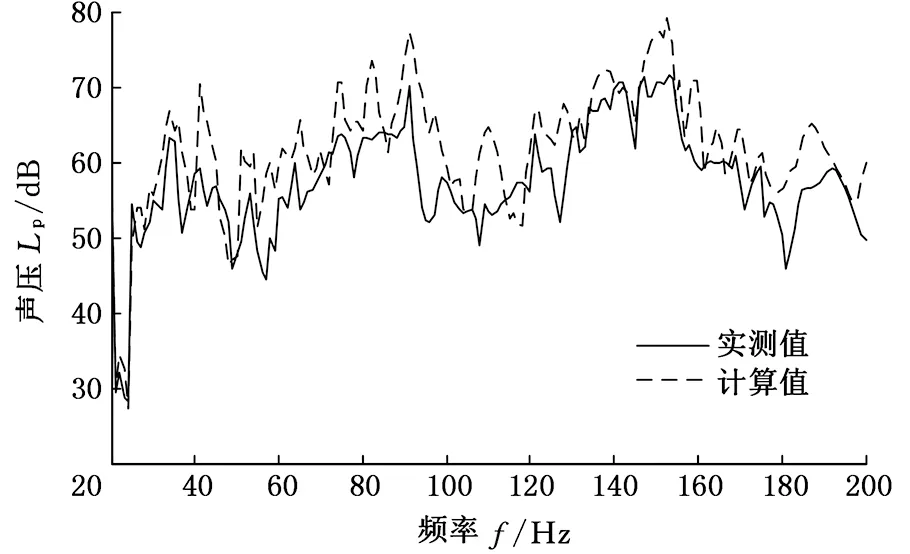
图7 左后悬置点-主驾右耳NTF实测值与计算值对比

由于实车行驶工况下驾驶室四个悬置点同时受到激励，所以在之前建立的声固耦合模型的四个悬置点处同时施加竖直方向单位激励力，利用声固耦合有限元法分别计算驾驶室优化前后的内部声场，其中驾驶员右耳位置处声压计算结果如图8所示。

图8 轻量化前后驾驶员右耳处声压对比

对比图8轻量化前后驾驶员右耳处声压可以看出，在60 Hz之前频率段的几个峰值声压有所降低，这是由于在优化变量选择和优化约束中考虑和控制了低阶模态。总体来看，轻量化之后的声压值均方根比优化前提高了1.4 dB。

5 结论

(1)建立驾驶室结构有限元模型并通过数值仿真与试验模态结果对比验证了模型准确性，继而分析驾驶室静态弯曲和扭转刚度。

(2)提出加权相对灵敏度概念并根据其分析结果确定设计变量及其优化方向，提高了优化变量选择的准确性，进而提升了优化过程中的计算效率，确保了轻量化设计的成功实施。

(3)通过优化设计，驾驶室在总质量减轻8.7%的同时，刚度和模态性能均有相应提高，车内噪声水平变化不大，这对驾驶室的轻量化设计和整车构件的优化具有一定的参考意义。

[1] Benedyk J. Light Metal in Automotive Applications. [J]. Light Metal Age,2000,58(10):34-35.

[2] 邱国华，汪侃磊，杨亭福.车身轻量化技术路径发展研究[J].上海汽车，2015(6):40-45. Qiu Guohua，Wang Kanlei，Yang Tingfu. A Study on the Development of Light weighting of Car Body[J]. Shanghai Auto，2015(6):40-45.

[3] 韩旭，朱平，余海东.基于刚度和模态性能的轿车驾驶室轻量化研究[J].汽车工程，2007,29(7):545-549. Han Xu，Zhu Ping，Yu Haidong. A Study on the Weight Reduction of Car_body with Required stiffness and Modal Performances[J]. Automotive Enginneering，2007,29(7):545-549.

[4] 施 颐，朱 平，张 宇，等.基于刚度与耐撞性要求的车身结构轻量化研究[J].汽车工程，2010,32(9):19-24. Shi Yi，Zhu Ping，Zhang Yu，et al. A Study on the Light Weighting of Car Body Structure Based on Stiffness and Crash Worthiness Requirements[J]. Automotive Enginneering，2010,32(9):19-24.

[5] 叶 辉，胡 平，申国哲，等.基于灵敏度和碰撞仿真的汽车车身轻量化优化设计[J].农业机械学报，2010,41(10):24-28,33. Ye Hui，Hu Ping，Shen Guozhe，et al. Light Weight Optimization Design of Car Body Based on Sensitivity and Side Crash Simulation[J]. Transactions of the Chinese Society for Agricultural Machinery，2010,41(10):24-28,33.

[6] 史国宏，陈 勇，杨雨泽.白车身多学科轻量化优化设计应用[J].机械工程学报，2012,48(8):114-118. Shi Guohong，Chen Yong，Yang Yuze. BIW Architecture Multidisciplinary Light Weight Optimization Design[J]. Journal of Mechanical Engineering，2012,48(8):114-118.

[7] 高云凯，王婧人，汪翼.基于正交试验的大型客车车身结构多工况拓扑优化研究[J].汽车科技，2011(11):16-19.. Gao Yunkai，Wang Jingren，Wang Yi. Multi-case Topology Optimization of Bus Body Structure Based on Orthogonal Test[J].Auto Sci-Tech，2011(11):16-19.

[8] 王登峰，卢放.基于多学科优化设计方法的白驾驶室轻量化[J].吉林大学学报(工学版)，2015,45(1):29-37. Wang Dengfeng，Lu Fang. Body-in-white Lightweight Based on Multidisciplinary Design Optimization[J]. Journal of Jilin University ( Engineering and Technology Edition)，2015,45(1):29-37.

[9] 兰凤崇，赖番结，陈吉清，等.考虑动态特性的多工况驾驶室结构拓扑优化研究[J].机械工程学报，2014,50(20):122-128. Lan Fengchong，Lai Fanjie，Chen Jiqing，et al. Multi-case Topology Optimization of Body Structure Considering Dynamic Characteristic[J]. Journal of Mechanical Engineering，2014,50(20):122-128.

[10] Satty T L，Vargas L G. Models, Methods, Concepts & Applications of the Analytic Hierarchy Process[M]. 2nd ed. New York：Springer，2012.

[11] 智淑亚. 汽车车身结构与设计[M]. 北京: 机械工业出版社， 2014.

[12] 马鸣图，路洪洲，李志刚.论轿车白车身轻量化的表征参量和评价方法[J].汽车工程，2009,31(5):403-406. Ma Mingtu，Lu Hongzhou，Li Zhigang. On the Description Parameters and Evaluation Method for Light weighting of Car Body-in-white[J]. Automotive Enginneering，2009,31(5):403-406.

[13] 季枫.白车身参数化建模与多目标轻量化优化设计方法研究[D]. 长春: 吉林大学,2014.

[14] 陈剑，蒋丰鑫，肖悦.挖掘机驾驶室低频噪声分析与控制[J].中国机械工程，2014,25(15):2124-2129. Chen Jian，Jiang Fengxin，Xiao Yue. Low Frequency Noise Analysis and Control of Excavator Cab[J]. China Mechanical Engineering，2014,25(15):2124-2129.

(编辑 王艳丽)

Applications of Weighted Relative Sensitivity Analyses in Lightweighting of Cab Structures

Chen Jian Du Xuanfu Shi Feibo

Hefei University of Technology,Hefei,230009

A credible structure FE model of a cab was built and the model was verified by tests. The sensitivity of the cab components was calculated directly and the weight coefficients of constraint responses were determined through the analytic hierarchy process with consideration to variable margins of the constraint responses. Then a concept of weighted relative sensitivity was put forward and identified the design variables and its optimization directions according to the concept. The thicknesses of cab components were optimized on the promise of no reduction on the main static and dynamic performance of the cab. The objective is realized with the total mass of the cab is reduced by 8.7%, while the main static and dynamic performances are somewhat raised and the overall low-frequency noise levels rise lightly.

weighted relative sensitivity; modal analysis; stiffness; lightweighting

2016-02-02

U463.82

10.3969/j.issn.1004-132X.2016.24.023

陈 剑，男，1962年生。合肥工业大学噪声振动工程研究所所长、教授、博士研究生导师。研究方向为汽车NVH与CAE、机器低噪声设计、声质量设计等。发表论文150余篇。杜选福(通信作者)，男，1992年生。合肥工业大学噪声振动工程研究所硕士研究生。施斐博，男，1990年生。合肥工业大学噪声振动工程研究所硕士研究生。